13.4: Movimiento en el Espacio

Objetivos de aprendizaje

• Describir los vectores de velocidad y aceleración de una partícula que se mueve en el espacio.
• Explicar los componentes tangenciales y normales de la aceleración.
• Leyes estatales del movimiento planetario de Kepler.

Ahora hemos visto cómo describir las curvas en el plano y en el espacio, y cómo determinar sus propiedades, como la longitud del arco y la curvatura. Todo esto lleva al objetivo principal de este capítulo, que es la descripción del movimiento a lo largo de curvas planas y curvas espaciales. Ahora tenemos todas las herramientas que necesitamos; en esta sección, juntamos estas ideas y miramos cómo usarlas.

Vectores de movimiento en el plano y en el espacio

Nuestro punto de partida es utilizar funciones vectoriales para representar la posición de un objeto en función del tiempo. Todo el material siguiente se puede aplicar ya sea a curvas en el plano o a curvas de espacio. Por ejemplo, cuando miramos la órbita de los planetas, las curvas que definen estas órbitas se encuentran todas en un plano porque son elípticas. Sin embargo, una partícula que viaja a lo largo de una hélice se mueve en una curva en tres dimensiones.

Definición: Velocidad, Velocidad y Aceleración

Let\(\vecs r(t)\) Ser una función vectorial-valorada dos veces diferenciable del parámetro\(t\) que representa la posición de un objeto en función del tiempo.

El vector\(\vecs v(t)\) de velocidad del objeto viene dado por

\[\text{Velocity}\,=\vecs v(t)=\vecs r′(t). \label{Eq1} \]

El vector de aceleración\(\vecs a(t)\) se define como

\[\text{Acceleration}\,=\vecs a(t)=\vecs v′(t)=\vecs r″(t). \label{Eq2} \]

La velocidad se define para ser

\[\mathrm{Speed}\,=v(t)=‖\vecs v(t)‖=‖\vecs r′(t)‖=\dfrac{ds}{dt}. \label{Eq3} \]

Dado que\(\vecs{r}(t)\) pueden estar en dos o tres dimensiones, estas funciones con valores vectoriales pueden tener dos o tres componentes. En dos dimensiones, definimos\(\vecs{r}(t)=x(t) \hat{\mathbf i}+y(t) \hat{\mathbf j}\) y en tres dimensiones\(\vecs r(t)=x(t) \hat{\mathbf i}+y(t) \hat{\mathbf j}+z(t) \hat{\mathbf k}\). Entonces la velocidad, la aceleración y la velocidad se pueden escribir como se muestra en la siguiente tabla.

Tabla\(\PageIndex{1}\): Fórmulas para Posición, Velocidad, Aceleración y Velocidad

Cantidad	Dos Dimensiones	Tres dimensiones
Posición	\(\vecs{r}(t)=x(t) \hat{\mathbf i}+y(t) \hat{\mathbf j}\)	\(\vecs{r}(t)=x(t) \hat{\mathbf i}+y(t) \hat{\mathbf j}+z(t) \hat{\mathbf k}\)
Velocity	\(\vecs{v}(t)=x′(t) \hat{\mathbf i}+y′(t) \hat{\mathbf j}\)	\(\vecs{v}(t)=x′(t) \hat{\mathbf i}+y′(t) \hat{\mathbf j}+z′(t) \hat{\mathbf k}\)
Aceleración	\(\vecs{a}(t)=x″(t) \hat{\mathbf i}+y″(t) \hat{\mathbf j}\)	\(\vecs{a}(t)=x″(t) \hat{\mathbf i}+y″(t) \hat{\mathbf j}+z″(t) \hat{\mathbf k}\)
Velocidad	\(\|\vecs{v}(t)\|= \sqrt{(x′(t))^2+(y′(t))^2}\)	\(\|\vecs{v}(t)\|=\sqrt{(x′(t))^2+(y′(t))^2+(z′(t))^2}\)

Ejemplo\(\PageIndex{1}\): Studying Motion Along a Parabola

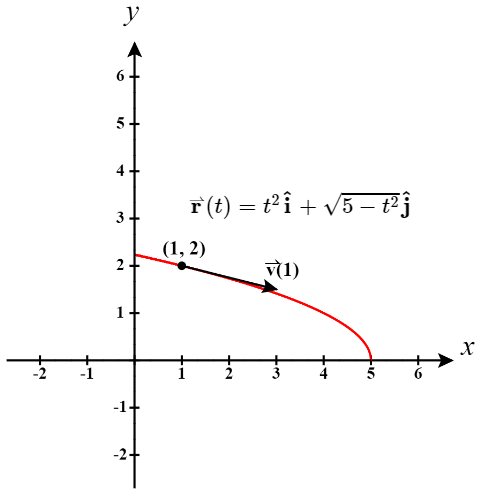
Una partícula se mueve en una trayectoria parabólica definida por la función de valor vectorial\(\vecs{r}(t)=t^2 \hat{\mathbf i}+ \sqrt{5−t^2} \hat{\mathbf j}\), donde\(t\) mide el tiempo en segundos.

1. Encuentra la velocidad, la aceleración y la velocidad como funciones del tiempo.
2. Dibuje la curva junto con el vector de velocidad en el momento\(t=1\).

Solución

1. Usamos Ecuaciones\ ref {Eq1},\ ref {Eq2}, y\ ref {Eq3}:

   \[ \begin{align*} \vecs{v}(t) &= \vecs{r}′(t)=2t\hat{\mathbf i}−\dfrac{t}{\sqrt{5-t^2}}\hat{\mathbf j} \\[4pt] \vecs{a}(t) &=\vecs{v}′(t)=2\hat{\mathbf i}−5(5−t^2)^{-\frac{3}{2}}\hat{\mathbf j} \\[4pt] ||\vecs{v}(t)|| &=||\vecs{r}′(t)|| \\[4pt] &=\sqrt{(2t)^2+\left(-\dfrac{t}{\sqrt{5-t^2}}\right)^2} \\[4pt] &=\sqrt{4t^2+\dfrac{t^2}{5-t^2}} \\[4pt] &=\sqrt{\dfrac{21t^2-4t^4}{5-t^2}}. \end{align*}\]

2. La gráfica de\(\vecs{r}(t)=t^2 \hat{\mathbf i}+ \sqrt{5−t^2} \hat{\mathbf j}\) es una porción de una parábola (Figura\(\PageIndex{1}\)).
   
   Cuando\(t=1\),\(\vecs r(1) = (1)^2 \mathbf{\hat i} + \sqrt{5-(1)^2} \mathbf{\hat j} \quad = \quad \mathbf{\hat i} + \sqrt{4} \mathbf{\hat j} \quad = \quad \mathbf{\hat i} + 2 \mathbf{\hat j}\).
   
   Así la partícula se ubicaría en el punto\((1, 2)\) cuando\(t =1\).
   
   El vector de velocidad en\(t=1\) es

   \[ \begin{align*} \vecs{v}(1) &=\vecs{r}′(1)=2(1)\hat{\mathbf i}−\frac{1}{\sqrt{5-1^2}} \hat{\mathbf j}\quad \\[4pt] &= \quad 2\hat{\mathbf i}−\frac{1}{2}\hat{\mathbf j} \end{align*}\]

   y el vector de aceleración en\(t=1\) es

   \[\vecs{a}(1)=\vecs{v}′(1)=2\hat{\mathbf i}−5(5 - 1^2)^{-3/2}\hat{\mathbf j}\quad = \quad 2\hat{\mathbf i}−\frac{5}{8}\hat{\mathbf j}. \nonumber \]

   Observe que el vector de velocidad es tangente a la trayectoria, como siempre es el caso.

Figura\(\PageIndex{1}\): Esta gráfica representa el vector de velocidad en el momento\(t=1\) para una partícula que se mueve en una trayectoria parabólica.

Ejercicio\(\PageIndex{1}\)

Una partícula se mueve en una trayectoria definida por la función de valor vectorial\(\vecs r(t)=(t^2−3t)\,\hat{\mathbf i}+(2t−4)\,\hat{\mathbf j}+(t+2)\,\hat{\mathbf k}\), donde\(t\) mide el tiempo en segundos y donde la distancia se mide en pies. Encuentra la velocidad, la aceleración y la velocidad como funciones del tiempo.

Pista

Usa Ecuaciones\ ref {Eq1},\ ref {Eq2}, y\ ref {Eq3}.

Responder

\[\begin{align*}\vecs v(t) &=\vecs{r}'(t) =(2t-3)\,\hat{\mathbf i}+2\,\hat{\mathbf j}+\,\hat{\mathbf k}\\[4pt] \vecs a(t) &=\vecs v′(t) =2\,\hat{\mathbf i} \end{align*}\]

\[ ||\vecs{r}′(t)||=\sqrt{(2t-3)^2+2^2+1^2} =\sqrt{4t^2-12t+14} \nonumber \]

Las unidades de velocidad y velocidad son pies por segundo, y las unidades para aceleración son pies por segundo al cuadrado.

Para comprender mejor los vectores de velocidad y aceleración, imagina que estás conduciendo por una carretera con curvas. Si no giras el volante, seguirías en línea recta y saldrías de la carretera. La velocidad a la que estás viajando cuando corres fuera de la carretera, junto con la dirección, da un vector que representa tu velocidad, como se ilustra en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): En cada punto de una carretera transitada por un automóvil, el vector de velocidad del automóvil es tangente al camino recorrido por el automóvil.

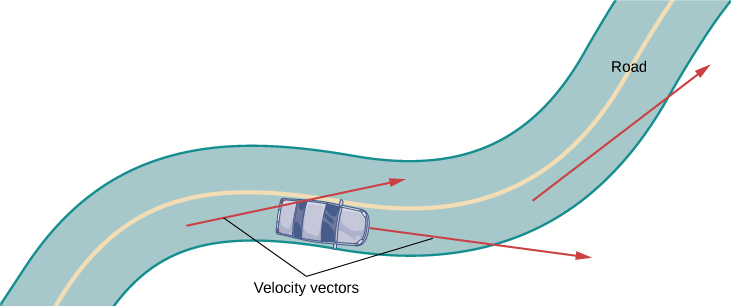
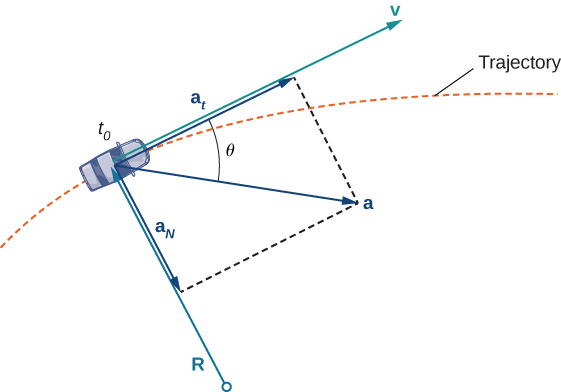
No obstante, el hecho de que debas girar el volante para permanecer en la carretera indica que tu velocidad siempre está cambiando (aunque tu velocidad no lo sea) porque tu dirección cambia constantemente para mantenerte en la carretera. Al girar a la derecha, su vector de aceleración también apunta hacia la derecha. Al girar hacia la izquierda, su vector de aceleración apunta hacia la izquierda. Esto indica que tus vectores de velocidad y aceleración están cambiando constantemente, independientemente de si tu velocidad real varía (Figura\(\PageIndex{3}\)).

Figura\(\PageIndex{3}\): La línea discontinua representa la trayectoria de un objeto (un automóvil, por ejemplo). El vector de aceleración apunta hacia el interior del giro en todo momento.

Componentes del vector de aceleración

Podemos combinar algunos de los conceptos discutidos en Longitud de Arco y Curvatura con el vector de aceleración para obtener una comprensión más profunda de cómo este vector se relaciona con el movimiento en el plano y en el espacio. Recordemos que el vector tangente unitario\(\vecs T\) y el vector normal unitario\(\vecs N\) forman un plano osculante en cualquier punto\(P\) de la curva definida por una función de valor vectorial\(\vecs{r}(t)\). El siguiente teorema muestra que el vector de aceleración\(\vecs{a}(t)\) se encuentra en el plano osculante y puede escribirse como una combinación lineal de la tangente unitaria y los vectores normales unitarios.

Teorema\(\PageIndex{1}\): The Plane of the Acceleration Vector

El vector\(\vecs{a}(t)\) de aceleración de un objeto que se mueve a lo largo de una curva trazada por una función diferenciable dos veces\(\vecs{r}(t)\) se encuentra en el plano formado por el vector tangente unitario\(\vecs T(t)\) y el vector normal de la unidad principal\(\vecs N(t)\) a\(C\). Además,

\[\vecs{a}(t) = v'(t)\vecs{T}(t) + [v(t)]^2 \kappa \vecs{N}(t) \nonumber \]

Aquí,\(v(t) = \|\vecs v(t)\|\) es la velocidad del objeto y\(\kappa\) es la curvatura de\(C\) trazado por\(\vecs{r}(t)\).

Prueba

Porque\(\vecs{v}(t)=\vecs{r}′(t)\) y\(\vecs{T}(t)=\dfrac{\vecs{r}′(t)}{||\vecs{r}′(t)||}\), tenemos\(\vecs v(t)=||\vecs{r}′(t)||\vecs{T}(t)=v(t)\vecs{T}(t)\).

Ahora diferenciamos esta ecuación:

\[\vecs{a}(t)=\vecs{v}′(t)=\dfrac{d}{dt}\left(v(t)\vecs{T}(t)\right)=v′(t)\vecs{T}(t)+v(t)\vecs{T}′(t) \nonumber \]

Ya que\(\vecs{N}(t)=\dfrac{\vecs{T}′(t)}{||\vecs{T}′(t)||}\), sabemos\(\vecs{T}′(t)=||\vecs{T}′(t)||\vecs{N}(t)\), así

\[\vecs{a}(t)=v′(t)\vecs{T}(t)+v(t)||\vecs{T}′(t)||\vecs{N}(t). \nonumber \]

Una fórmula para la curvatura es\(\kappa=\dfrac{||\vecs{T}'(t)||}{||\vecs{r}'(t)||}\), entonces\(\vecs{T}'(t) = \kappa ||\vecs{r}'(t) || = \kappa v(t) \).

Esto da\(\vecs{a}(t)=v′(t)\vecs{T}(t)+\kappa (v(t))^2 \vecs{N}(t).\)

\(\square\)

Los coeficientes de\(\vecs{T}(t)\) y\(\vecs{N}(t)\) se conocen como el componente tangencial de la aceleración y el componente normal de aceleración, respectivamente. Escribimos\(a_\vecs{T}\) para denotar el componente tangencial y\(a_\vecs{N}\) para denotar el componente normal.

Teorema\(\PageIndex{2}\): Tangential and Normal Components of Acceleration

Let\(\vecs{r}(t)\) Ser una función de valor vectorial que denota la posición de un objeto en función del tiempo. Entonces\(\vecs{a}(t)=\vecs{r}′′(t)\) está el vector de aceleración. Los componentes tangenciales y normales de la aceleración\(a_\vecs{T}\) y\(a_\vecs{N}\) están dados por las fórmulas

\[a_{\vecs{T}}=\vecs a \cdot\vecs{T}=\dfrac{\vecs{v}\cdot\vecs{a}}{||\vecs{v}||} \label{Eq1B} \]

y

\[a_\vecs{N}=\vecs a\cdot \vecs N=\dfrac{||\vecs v \times \vecs a||}{||\vecs v||}=\sqrt{||\vecs a||^2−{\left(a_{\vecs{T}}\right)^2}}. \label{Eq2B} \]

Estos componentes están relacionados por la fórmula

\[\vecs{a}(t)=a_\vecs{T} \vecs{T}(t)+a_\vecs{N}\vecs{N}(t). \label{Eq3B} \]

Aquí\(\vecs{T}(t)\) está el vector tangente unitario a la curva definida por\(\vecs{r}(t)\), y\(\vecs{N}(t)\) es el vector de unidad normal a la curva definida por\(\vecs{r}(t)\).

El componente normal de la aceleración también se llama el componente centrípeta de la aceleración o, a veces, el componente radial de la aceleración. Para entender la aceleración centrípeta, supongamos que viaja en un automóvil sobre una vía circular a una velocidad constante. Entonces, como vimos antes, el vector de aceleración apunta hacia el centro de la pista en todo momento. Como piloto en el auto, sientes un tirón hacia el exterior de la pista porque estás girando constantemente. Esta sensación actúa en la dirección opuesta a la aceleración centrípeta. Lo mismo se aplica a los caminos no circulares. La razón es que tu cuerpo tiende a viajar en línea recta y resiste la fuerza resultante de la aceleración que lo empuja hacia un lado. Tenga en cuenta que\(B\) en el punto de\(\PageIndex{4}\) la Figura el vector de aceleración apunta hacia atrás. Esto se debe a que el auto está desacelerando a medida que entra en la curva.

Figura\(\PageIndex{4}\): Los componentes tangenciales y normales de la aceleración pueden ser utilizados para describir el vector de aceleración.

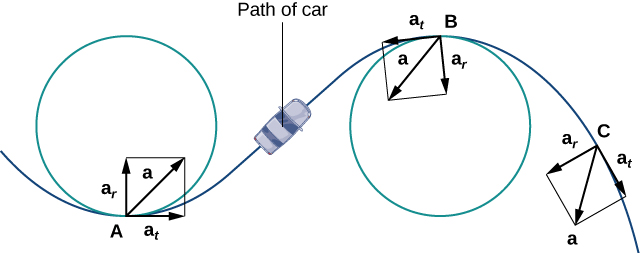
Los vectores unitarios tangenciales y normales en cualquier punto dado de la curva proporcionan un marco de referencia en ese punto. Los componentes tangencial y normal de la aceleración son las proyecciones del vector de aceleración sobre\(\vecs T\) y\(\vecs N\), respectivamente.

Ejemplo\(\PageIndex{2}\): Finding Components of Acceleration

Una partícula se mueve en una trayectoria definida por la función de valor vectorial\(\vecs{r}(t)=t^2\,\hat{\mathbf i}+(2t−3)\,\hat{\mathbf j}+(3t^2−3t)\,\hat{\mathbf k}\), donde\(t\) mide el tiempo en segundos y la distancia se mide en pies.

1. Encontrar\(a_\vecs{T}\) y\(a_\vecs{N}\) como funciones de\(t\).
2. Encuentra\(a_\vecs{T}\) y\(a_\vecs{N}\) a la hora\(t=2\).

Solución

1. Comencemos a derivar las funciones de velocidad y aceleración:

   \[\begin{align*} \vecs{v}(t) &= \vecs{r}'(t) \\[4pt] &= 2t\,\hat{\mathbf i}+2\,\hat{\mathbf j}+(6t-3)\,\hat{\mathbf k} \\[4pt] \vecs{a}(t) &= \vecs{v}'(t) \\[4pt] &=2\,\hat{\mathbf i}+6\,\hat{\mathbf k} \end{align*}\]Ahora aplicamos la Ecuación\ ref {Eq1B}:\[\begin{align*}a_{\vecs{T}} &=\dfrac{\vecs{v}\cdot \vecs{a}}{||\vecs{v} ||} \\[4pt] &= \dfrac{ (2t \,\hat{\mathbf i} +2\,\hat{\mathbf j} +(6t-3)\,\hat{\mathbf k})\cdot(2\,\hat{\mathbf i}+6\,\hat{\mathbf k}) }{|| 2t\,\hat{\mathbf i} + 2\,\hat{\mathbf j} + (6t-3)\,\hat{\mathbf k} ||} \\[4pt] &= \dfrac{4t + 6(6t-3)}{\sqrt{(2t)^2 +2^2 + (6t-3)^2}} \\[4pt] &= \dfrac{40t-18}{40t^2 - 36t+13} \end{align*}\] Ahora podemos aplicar la Ecuación\ ref {Eq2B}:

   \[\begin{align*} a_\vecs{N} &=\sqrt{||\vecs{a}||^2-\left(a_{\vecs{T}}\right)^2} \\[4pt] &= \sqrt{||2\,\hat{\mathbf i}+6\,\hat{\mathbf k}||^2 - \left( \dfrac{ 40t-18 }{\sqrt{40t^2-36t+13}} \right)^2} \\[4pt] &= \sqrt{ 4+36-\dfrac{(40t-18)^2}{40t^2-36t+13} } \\[4pt] &= \sqrt{\dfrac{ 40(40t^2-36t+13)-(1600t^2-1440t+324) }{40t^2-36t+13} } \\[4pt] &= \sqrt{ \dfrac{196}{ 40t^2-36t+13} } \\[4pt] &= \dfrac{14}{\sqrt{40t^2-36t+13}} \end{align*}\]

2. Debemos evaluar cada una de las respuestas de la parte a en\(t=2\):

   \[\begin{align*} a_{\vecs{T}}(2) &= \dfrac{ 40(2)-18 }{\sqrt{40(2)^2 - 36(2)+13 }} \\[4pt] &= \dfrac{80-18 }{\sqrt{160-72+13}} \\[4pt] &= \dfrac{62}{\sqrt{101}} \\[4pt] a_{\vecs{N}}(2) &= \dfrac{14}{\sqrt{40(2)^2 -36(2)+13 }} \\[4pt] &= \dfrac{14}{\sqrt{160-72+13}} = \dfrac{14}{\sqrt{101}}. \end{align*}\]

   Las unidades de aceleración son pies por segundo al cuadrado, al igual que las unidades de los componentes normal y tangencial de aceleración.

Ejercicio\(\PageIndex{2}\)

Un objeto se mueve en una ruta definida por la función de valor vectorial\(\vecs r(t)=4t\,\hat{\mathbf i}+t^2\,\hat{\mathbf j}\), donde\(t\) mide el tiempo en segundos.

1. Encontrar\(a_\vecs{T}\) y\(a_\vecs{N}\) como funciones de\(t\).
2. Encuentra\(a_\vecs{T}\) y\(a_\vecs{N}\) a la hora\(t=−3\).

Pista

Usa Ecuaciones\ ref {Eq1B} y\ ref {Eq2B}

Responder

a.\[\begin{align*} a_\vecs{T} =\dfrac{\vecs v(t) \cdot \vecs a(t)}{||\vecs v(t)||}= \dfrac{\vecs r'(t) \cdot \vecs r''(t) }{||\vecs r'(t)||} \\ = \dfrac{ (4\,\hat{\mathbf i} + 2t \,\hat{\mathbf j}) \cdot (2\,\hat{\mathbf j}) }{||4\,\hat{\mathbf i} + 2t \,\hat{\mathbf j} ||} \\ = \dfrac{4t}{\sqrt{4^2 + (2t)^2}}\\ = \dfrac{2t}{\sqrt{2+t^2}} \end{align*}\]
\[\begin{align*} a_\vecs{N} = \sqrt{||\vecs a||^2-a_\vecs{T}^2}\\ =\sqrt{||2\,\hat{\mathbf j} ||^2 - \left(\dfrac{2t}{\sqrt{2+t^2}}\right)^2} \\ =\sqrt{ 4 - \dfrac{4t^2 }{2+t^2} } \end{align*}\]

b.\[\begin{align*} a_\vecs{T}(−3) = \dfrac{2(-3)}{\sqrt{2+(-3)^2}} \\ = \dfrac{-6}{\sqrt{11}}\end{align*}\]
\[\begin{align*}a_\vecs{N}(−3) = \sqrt{ 4 - \dfrac{4(-3)^2 }{2+(-3)^2} } \\ = \sqrt{4- \dfrac{36}{11}} \\ = \sqrt{\dfrac{8}{11} }\\ =\dfrac{2\sqrt{2}}{\sqrt{11}} \end{align*}\]

Movimiento de proyectiles

Ahora veamos una aplicación de funciones vectoriales. En particular, consideremos el efecto de la gravedad en el movimiento de un objeto a medida que viaja por el aire, y cómo determina la trayectoria resultante de ese objeto. A continuación, ignoramos el efecto de la resistencia al aire. Esta situación, con un objeto moviéndose con una velocidad inicial pero sin fuerzas que actúen sobre él que no sean la gravedad, se conoce como movimiento de proyectil. Describe el movimiento de objetos desde pelotas de golf hasta pelotas de beisbol, y de flechas a balas de cañón.

Primero tenemos que elegir un sistema de coordenadas. Si estamos parados en el origen de este sistema de coordenadas, entonces elegimos el\(y\) eje positivo para estar arriba, el eje negativo\(y\) para estar abajo, y el eje positivo\(x\) para estar hacia adelante (es decir, lejos del lanzador del objeto). El efecto de la gravedad es en dirección descendente, por lo que la segunda ley de Newton nos dice que la fuerza sobre el objeto resultante de la gravedad es igual a la masa del objeto multiplicada por la aceleración resultante de la gravedad, o\(\vecs F_g=m\vecs a\), donde\(\vecs F_g\) representa la fuerza de la gravedad y\(\vecs a = -g\,\hat{\mathbf j}\) representa la aceleración resultante de la gravedad en la superficie de la Tierra. El valor de\(g\) en el sistema inglés de medición es aproximadamente 32 pies/seg ² y es aproximadamente 9.8 m/seg ² en el sistema métrico. Esta es la única fuerza que actúa sobre el objeto. Dado que la gravedad actúa en dirección descendente, podemos escribir la fuerza resultante de la gravedad en la forma\(\vecs F_g=−mg\,\hat{\mathbf j}\), como se muestra en la Figura\(\PageIndex{5}\).

Figura\(\PageIndex{5}\): Un objeto está cayendo bajo la influencia de la gravedad.

La segunda ley de Newton también nos dice eso\(F=m\vecs{a}\), donde\(\vecs a\) representa el vector de aceleración del objeto. Esta fuerza debe ser igual a la fuerza de gravedad en todo momento, por lo que sabemos que

\[\begin{align*} \vecs F =\vecs F_g \\ m\vecs{a} = -mg \,\hat{\mathbf j} \\ \vecs{a} = -g\,\hat{\mathbf j}. \end{align*}\]

Ahora usamos el hecho de que el vector de aceleración es la primera derivada del vector de velocidad. Por lo tanto, podemos reescribir la última ecuación en la forma

\[\vecs v'(t) = -g\,\hat{\mathbf j} \nonumber \]

Al tomar la antiderivada de cada lado de esta ecuación obtenemos

\[ \vecs v(t) = \int -g \,\hat{\mathbf j}\; dt = -gt\,\hat{\mathbf j} + \vecs C_1 \nonumber \]

para algún vector constante\(\vecs C_1\). Para determinar el valor de este vector, podemos usar la velocidad del objeto en un tiempo fijo, digamos a la vez\(t=0\). Llamamos a esta velocidad la velocidad inicial:\(\vecs v(0)=\vecs v_0\). Por lo tanto,\(\vecs v(0)=−g(0)\,\hat{\mathbf j}+\vecs C_1=\vecs v_0\) y\(\vecs C_1= \vecs v_0\). Esto da el vector de velocidad como\(\vecs v(t)=−gt\,\hat{\mathbf j}+\vecs v_0\).

A continuación utilizamos el hecho de que la velocidad\(\vecs{v}(t)\) es la derivada de la posición\(\vecs{s}(t)\). Esto da la ecuación

\[\vecs s'(t)=-gt\,\hat{\mathbf j}+\vecs{v}_0. \nonumber \]

Tomando la antiderivada de ambos lados de esta ecuación lleva a

\[\begin{align*} \vecs s(t) &= \int -gt\,\hat{\mathbf j} + \vecs{v}_0 \;dt \\[4pt] &= -\dfrac{1}{2}gt^2 \,\hat{\mathbf j} + \vecs{v}_0 t + \vecs{C}_2 \end{align*}\]

con otro vector constante desconocido\(\vecs{C}_2\). Para determinar el valor de\(\vecs{C}_2\), podemos usar la posición del objeto en un momento dado, digamos a la vez\(t=0\). Llamamos a esta posición la posición inicial:\(\vecs{s}(0)=\vecs{s}_0\). Por lo tanto,\(\vecs{s}(0)=−(1/2)g(0)^2\,\hat{\mathbf j}+\vecs{v}_0(0)+\vecs{C}_2=\vecs{s}_0\). Esto da la posición del objeto en cualquier momento como

\[ \vecs{s}(t)=−\dfrac{1}{2}gt^2 \,\hat{\mathbf j}+\vecs{v}_0 t+\vecs{s}_0. \nonumber \]

Echemos un vistazo más de cerca a la velocidad inicial y la posición inicial. En particular, supongamos que el objeto es arrojado hacia arriba desde el origen en ángulo con respecto\(\theta\) a la horizontal, con velocidad inicial\(\vecs{v}_0\). ¿Cómo podemos modificar el resultado anterior para reflejar este escenario? Primero, podemos suponer que se lanza desde el origen. Si no, entonces podemos mover el origen hasta el punto desde donde se lanza. Por lo tanto\(\vecs{s}_0=\vecs{0}\),, como se muestra en la Figura\(\PageIndex{6}\).

Figura\(\PageIndex{6}\): Movimiento del proyectil cuando el objeto es lanzado hacia arriba en un ángulo θ. El movimiento horizontal es a velocidad constante y el movimiento vertical es a aceleración constante.

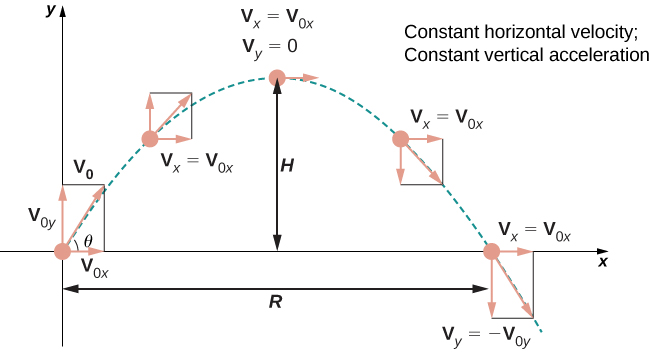
Podemos reescribir el vector de velocidad inicial en la forma\(\vecs{v}_0= v_0 \cos \theta \,\hat{\mathbf i} + v_0 \sin \theta \,\hat{\mathbf j}\). Entonces la ecuación para la función de posición\(\vecs{s}(t)\) se convierte

\[\begin{align*} \vecs{s}(t) &=-\dfrac{1}{2} gt^2\,\hat{\mathbf j} + v_0 t \cos\theta \,\hat{\mathbf i} + v_0 t \sin\theta \,\hat{\mathbf j} \\[4pt] &= v_0 t \cos\theta\,\hat{\mathbf i} + v_0 t \sin\theta \,\hat{\mathbf j} - \dfrac{1}{2} gt^2\,\hat{\mathbf j} \\[4pt] &= v_0 t \cos\theta \,\hat{\mathbf i} + \left(v_0 t \sin\theta - \dfrac{1}{2} gt^2\right)\,\hat{\mathbf j}. \end{align*}\]

El coeficiente de\(\hat{\mathbf i}\) representa la componente horizontal de\(\vecs{s}(t)\) y es la distancia horizontal del objeto desde el origen en el momento\(t\). El valor máximo de la distancia horizontal (medida a la misma altitud inicial y final) se denomina rango\(R\). El coeficiente de\(\hat{\mathbf j}\) representa la componente vertical de\(\vecs{s}(t)\) y es la altitud del objeto en el momento\(t\). El valor máximo de la distancia vertical es la altura\(H\).

Ejemplo\(\PageIndex{3}\): Motion of a Cannonball

Durante una celebración del Día de la Independencia, se dispara una bala de cañón desde un cañón en un acantilado hacia el agua. El cañón está dirigido a un ángulo de 30° por encima de la horizontal y la velocidad inicial de la bala de cañón es de 600 pies/seg. El acantilado está a 100 pies sobre el agua (Figura\(\PageIndex{7}\)).

1. Encuentra la altura máxima de la bala de cañón.
2. ¿Cuánto tiempo tardará la bala de cañón en chapotear en el mar?
3. ¿A qué distancia del mar golpeará la bala de cañón al agua?

Figura\(\PageIndex{7}\): El vuelo de una bala de cañón (ignorando la resistencia del aire) es el movimiento del proyectil.

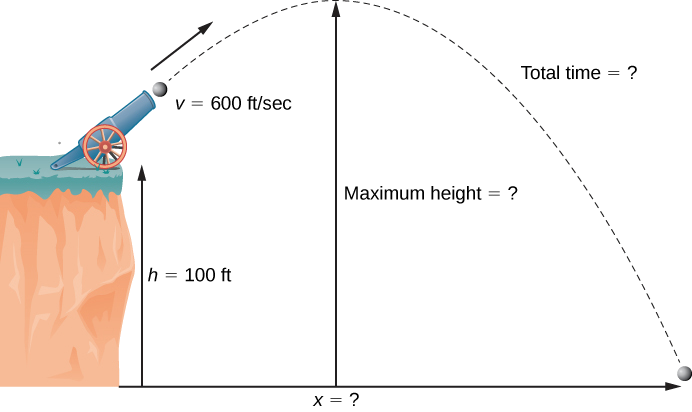
Solución

Usamos la ecuación

\[\vecs{s}(t) = v_0 t \cos\theta \,\hat{\mathbf i} + \left(v_0 t \sin\theta - \dfrac{1}{2}gt^2 \right)\,\hat{\mathbf j} \nonumber \]

con\(\theta=30^\circ \),\(g=32 \dfrac{\text{ft}}{\text{sec}^2}\), y\(v_0=600 \dfrac{\text{ft}}{\text{sec}^2}\). Entonces la ecuación de posición se convierte

\[\begin{align*} \vecs{s}(t) &= 600 t ( \cos 30^\circ)\,\hat{\mathbf i} + \left(600t \sin30^\circ - \dfrac{1}{2}(32)t^2 \right)\,\hat{\mathbf j} \\[4pt] &= 300t\sqrt{3} \,\hat{\mathbf i} + \left( 300t - 16t^2 \right)\,\hat{\mathbf j} \end{align*}\]

1. La bala de cañón alcanza su altura máxima cuando la componente vertical de su velocidad es cero, porque la bala de cañón no está subiendo ni cayendo en ese punto. El vector de velocidad es

   \[\begin{align*} \vecs{v}(t) &=\vecs s'(t)\\[4pt] &= 300 \sqrt{3} \,\hat{\mathbf i} + (300-32t)\,\hat{\mathbf j} \end{align*} \nonumber \]

   Por lo tanto, la componente vertical de la velocidad viene dada por la expresión\(300−32t\). Establecer esta expresión igual a cero y resolver para t da\(t=9.375\) sec. La altura de la bala de cañón en este momento viene dada por el componente vertical del vector de posición, evaluado en\(t=9.375\).

   \[\begin{align*} \vecs{s}(9.375) &=300(9.375)\sqrt{3}\,\hat{\mathbf i}+(300(9.375)−16(9.375)^2)\,\hat{\mathbf j} \\[4pt] &=4871.39 \,\hat{\mathbf i}+1406.25\,\hat{\mathbf j} \end{align*}\]

   Por lo tanto, la altura máxima de la bala de cañón es de 1406.39 pies sobre el cañón, o 1506.39 pies sobre el nivel del mar.
2. Cuando la bala de cañón aterriza en el agua, está a 100 pies por debajo del cañón. Por lo tanto, el componente vertical del vector de posición es igual a −100. Ajustando el componente vertical de\(\vecs s(t)\) igual a −100 y resolviendo, obtenemos

   \[\begin{align*} 300t-16t^2 &= -100 \\ 16t^2-300t-100 =0 \\4t^2-75-25 =0 \\[4pt] t &= \dfrac{75\pm \sqrt{(-75)^2}-4(4)(-25) }{2(4)} \\[4pt] &= \dfrac{75 \pm \sqrt{6025}}{8} \\[4pt] &= \dfrac{75 \pm 5\sqrt{241}}{8} \end{align*}\]

   El valor positivo de\(t\) que resuelve esta ecuación es aproximadamente 19.08. Por lo tanto, la bala de cañón golpea el agua después de aproximadamente 19.08 seg.
3. Para encontrar la distancia al mar, simplemente sustituimos la respuesta de la parte (b) a\(\vecs{s}(t)\):

   \[\begin{align*} \vecs s(19.08) &=300(19.08)\sqrt{3} \,\hat{\mathbf i}+\left(300(19.08)−16(19.08)^2\right)\,\hat{\mathbf j}\\[4pt] &=9914.26\,\hat{\mathbf i}−100.7424\,\hat{\mathbf j} \end{align*}\]

   Por lo tanto, la pelota golpea el agua a unos 9914.26 pies de distancia de la base del acantilado. Observe que el componente vertical del vector de posición está muy cerca de −100, lo que nos indica que la pelota acaba de golpear el agua. Tenga en cuenta que 9914.26 pies no es el verdadero alcance del cañón ya que la bala de cañón aterriza en el océano en una ubicación debajo del cañón. El alcance del cañón se determinaría al encontrar qué tan lejos está la bala de cañón cuando su altura está a 100 pies sobre el agua (lo mismo que la altitud del cañón).

Ejercicio\(\PageIndex{3}\)

Un arquero dispara una flecha en un ángulo de 40° sobre la horizontal con una velocidad inicial de 98 m/seg. La altura del arquero es de 171.5 cm. Encuentra la distancia horizontal que recorre la flecha antes de que golpee el suelo.

Pista

La ecuación para el vector de posición necesita tener en cuenta la altura del arquero en metros.

Responder

967.15 m

Queda una última pregunta: En general, ¿cuál es la distancia máxima que puede recorrer un proyectil, dada su velocidad inicial? Para determinar esta distancia, asumimos que el proyectil se dispara desde el nivel del suelo y deseamos que regrese al nivel del suelo. En otras palabras, queremos determinar una ecuación para el rango. En este caso, la ecuación del movimiento del proyectil es

\[\vecs{s}=v_0 t \cos\theta \,\hat{\mathbf i} + \left(v_0t\sin\theta - \dfrac{1}{2}gt^2 \right)\,\hat{\mathbf j}. \nonumber \]

Establecer el segundo componente igual a cero y resolver\(t\) rendimientos

\[\begin{align*} v_0 t \sin\theta - \dfrac{1}{2}gt^2 =0\\ t\left(v_0 \sin\theta - \dfrac{1}{2}gt\right) =0 \end{align*}\]

Por lo tanto, ya sea\(t=0\) o\(t=\dfrac{2v_0\sin\theta}{g}\). Nos interesa el segundo valor de\(t\), así que sustituimos esto en\(\vecs{s}(t)\), lo que da

\[\begin{align*} \vecs{s}\left(\dfrac{2v_0\sin\theta}{g} \right) = v_0 \left(\dfrac{2v_0\sin\theta}{g} \right) \cos\theta \,\hat{\mathbf i} + \left( v_0\left(\dfrac{2v_0\sin\theta}{g} \right)\sin\theta - \dfrac{1}{2}g\left(\dfrac{2v_0\sin\theta}{g} \right)^2 \right)\,\hat{\mathbf j} \\ = \left(\dfrac{2v_0^2\sin\theta\cos\theta}{g} \right)\,\hat{\mathbf i} \\ = \dfrac{v_0^2 \sin2\theta}{g}\,\hat{\mathbf i}. \end{align*}\]

Así, la expresión para el alcance de un proyectil disparado en ángulo\(\theta\) es

\[R=\dfrac{v_0^2 \sin2\theta}{g}\,\hat{\mathbf i} . \nonumber \]

La única variable en esta expresión es\( \theta\). Para maximizar la distancia recorrida, tome la derivada del coeficiente de i con respecto a\(\theta\) y configúrela igual a cero:

\[\begin{align*} \dfrac{d}{d\theta} \left( \dfrac{v_0^2 \sin2\theta}{g} \right) =0\\ \dfrac{2v_0^2\cos2\theta}{g} =0\\ \theta=45^\circ \end{align*}\]

Este valor de\(\theta)\) es el valor positivo más pequeño que hace que la derivada sea igual a cero. Por lo tanto, en ausencia de resistencia al aire, el mejor ángulo para disparar un proyectil (para maximizar el alcance) es en un ángulo de 45°. La distancia que recorre viene dada por

\[\vecs{s}\left(\dfrac{2v_0 \sin 45^\circ}{g} \right)= \dfrac{v_0^2 \sin 90^\circ}{g} \,\hat{\mathbf i} = \dfrac{v_0^2}{g}\,\hat{\mathbf i} \nonumber \]

Por lo tanto, el rango para un ángulo de 45° es\(\frac{v_0^2}{g}\) unidades.

Leyes de Kepler

A principios del siglo XVII, Johannes Kepler pudo utilizar los datos asombrosamente precisos de su mentor Tycho Brahe para formular sus tres leyes del movimiento planetario, ahora conocidas como las leyes del movimiento planetario de Kepler. Estas leyes también se aplican a otros objetos del sistema solar en órbita alrededor del Sol, como los cometas (por ejemplo, el cometa Halley) y los asteroides. Variaciones de estas leyes se aplican a los satélites en órbita alrededor de la Tierra.

Teorema\(\PageIndex{2}\): Kepler's Laws of Planetary Motion

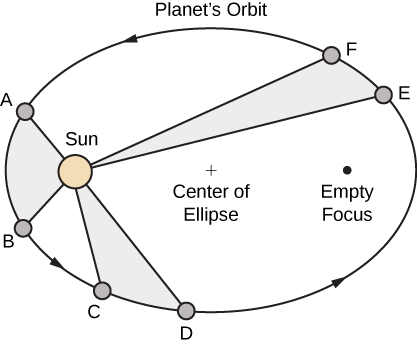
1. El camino de cualquier planeta alrededor del Sol es de forma elíptica, con el centro del Sol ubicado en un foco de la elipse (la ley de las elipses).
2. Una línea trazada desde el centro del Sol hasta el centro de un planeta barre áreas iguales en intervalos de tiempo iguales (la ley de áreas iguales) (Figura\(\PageIndex{8}\)).
3. La relación de los cuadrados de los períodos de dos planetas cualesquiera es igual a la proporción de los cubos de las longitudes de sus ejes orbitales semimajores (la Ley de Armonías).

Figura\(\PageIndex{8}\): La primera y segunda leyes de Kepler se muestran aquí. El Sol se encuentra en un foco de la órbita elíptica de cualquier planeta. Además, las áreas sombreadas son todas iguales, asumiendo que la cantidad de tiempo medida a medida que el planeta se mueve es la misma para cada región.

La tercera ley de Kepler es especialmente útil cuando se utilizan las unidades adecuadas. En particular, 1 unidad astronómica se define como la distancia promedio de la Tierra al Sol, y ahora se reconoce que es 149,597,870,700 m o, aproximadamente 93,000,000 mi. Por lo tanto, escribimos 1 A.U. = 93,000,000 mi. Dado que el tiempo que tarda la Tierra en orbitar el Sol es de 1 año, utilizamos años terrestres para unidades de tiempo. Entonces, sustituyendo 1 año por el periodo de la Tierra y 1 A.U. por la distancia promedio al Sol, la tercera ley de Kepler puede escribirse como

\[ T_p^2=D_p^3 \nonumber \]

para cualquier planeta del sistema solar, donde\(T_P\) es el periodo de ese planeta medido en años terrestres y\(D_P\) es la distancia promedio de ese planeta al Sol medida en unidades astronómicas. Por lo tanto, si conocemos la distancia promedio de un planeta al Sol (en unidades astronómicas), entonces podemos calcular la longitud de su año (en años terrestres), y viceversa.

Las leyes de Kepler se formularon con base en observaciones de Brahe; sin embargo, no fueron probadas formalmente hasta que Sir Isaac Newton pudo aplicar cálculo. Además, Newton pudo generalizar la tercera ley de Kepler a otros sistemas orbitales, como una luna que orbita alrededor de un planeta. La tercera ley original de Kepler solo se aplica a los objetos que orbitan el Sol.

Prueba

Ahora probemos la primera ley de Kepler utilizando el cálculo de funciones con valores vectoriales. Primero necesitamos un sistema de coordenadas. Coloquemos al Sol en el origen del sistema de coordenadas y dejemos que la función vectorizada\(\vecs{r}(t)\) represente la ubicación de un planeta en función del tiempo. Newton probó la ley de Kepler usando su segunda ley del movimiento y su ley de la gravitación universal. La segunda ley del movimiento de Newton puede escribirse como\(\vecs{F}=m\vecs{a}\), donde\(\vecs{F}\) representa la fuerza neta que actúa sobre el planeta. Su ley de gravitación universal puede escribirse en la forma\(\vecs{F}=−\dfrac{GmM}{||\vecs{r}||^2}\cdot \dfrac{\vecs{r}}{||\vecs{r} ||}\), lo que indica que la fuerza resultante de la atracción gravitacional del Sol apunta de nuevo hacia el Sol, y tiene magnitud\(\dfrac{GmM}{||\vecs{r}||^2} \) (Figura\(\PageIndex{9}\)).

Figura\(\PageIndex{9}\): La fuerza gravitacional entre la Tierra y el Sol es igual a la masa de la tierra multiplicada por su aceleración.

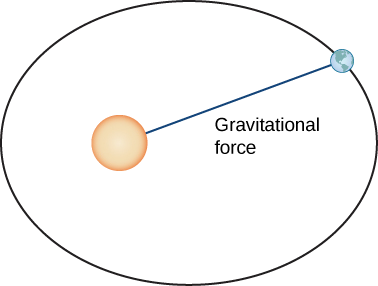
Estableciendo estas dos fuerzas iguales entre sí, y usando el hecho de que\(\vecs a(t)=\vecs v′(t)\), obtenemos

\[ m\vecs v′(t)=−\frac{GmM}{‖\vecs r‖^2}⋅\frac{\vecs r}{‖\vecs r‖}, \nonumber \]

que se puede reescribir como

\[ \dfrac{d\vecs v}{dt}=−\dfrac{GM}{||\vecs r||^3}\vecs{r}. \nonumber \]

Esta ecuación muestra que los vectores\(d\vecs{v}/dt\) y\(\vecs r\) son paralelos entre sí, así\(d\vecs {v}/dt \times \vecs {r}=\vecs 0\). A continuación, diferenciemos\(\vecs{r} \times \vecs{v}\) con respecto al tiempo:

\[\dfrac{d}{dt}(\vecs{r}\times \vecs{v})=\dfrac{d\vecs{r}}{dt}\times \vecs v+\vecs{r} \times \dfrac{d\vecs{v}}{dt}=\vecs{v}\times \vecs{v}+\vecs{0}=\vecs{0}. \label{Eq10} \]

Esto demuestra que\(\vecs{r}\times\vecs{v}\) es un vector constante, al que llamamos\(\vecs C\). Dado que\(\vecs r\) y ambos\(\vecs v\) son perpendiculares a\(\vecs C\) para todos los valores de\(t\), deben estar en un plano perpendicular a\(\vecs C\). Por lo tanto, el movimiento del planeta yace en un plano.

A continuación calculamos la expresión\(d\vecs{v}/dt\times \vecs C\):

\[\dfrac{d\vecs{v}}{dt} \times \vecs{C}=−\dfrac{GM}{||\vecs{r}||^3}\vecs{r}\times (\vecs{r}\times\vecs{v})=−\dfrac{GM}{||\vecs r||^3}[(\vecs{r} \cdot \vecs{v})\vecs{r} - (\vecs{r} \cdot \vecs{r})\vecs{v}]. \label{Eq11} \]

La última igualdad en la Ecuación\ ref {Eq10} es de la fórmula del producto de triple cruz (Introducción a los vectores en el espacio). Necesitamos una expresión para\(\vecs{r}\cdot \vecs{v}\). Para calcular esto, diferenciamos\(\vecs{r}\cdot \vecs{r}\) con respecto al tiempo:

\[ \dfrac{d}{dt}(\vecs{r}\cdot \vecs{r})=\dfrac{d\vecs{r}}{dt}\cdot \vecs{r}+\vecs{r}\cdot \dfrac{d\vecs{r}}{dt}=2\vecs{r}\cdot \dfrac{d\vecs{r}}{dt}=2\vecs{r}\cdot \vecs{v}. \label{Eq12} \]

Desde entonces\(\vecs{r}\cdot\vecs{r}=||\vecs r||^2\), también tenemos

\[\dfrac{d}{dt}(\vecs{r}\cdot \vecs{r})=\dfrac{d}{dt}||\vecs{r}||^2=2||\vecs{r}|| \dfrac{d}{dt}||\vecs{r}||. \label{Eq13} \]

Combinando la Ecuación\ ref {Eq12} y la Ecuación\ ref {Eq13}, obtenemos

\[\begin{align*} 2\vecs{r}\cdot \vecs{v} =2||\vecs{r}||\dfrac{d}{dt}||\vecs{r}|| \\ \vecs{r} \cdot \vecs{v} =||\vecs{r}‖\dfrac{d}{dt}||\vecs{r}||. \end{align*} \label{Eq14} \]

Sustituir esto en la Ecuación\ ref {Eq11} nos da

\[\begin{align} \dfrac{d\vecs{v}}{dt} \times \vecs{C} = - \dfrac{GM}{||\vecs{r}||^3} [(\vecs{r}\cdot \vecs{v})\vecs{r} - (\vecs{r}\cdot \vecs{r})\vecs{v}] \nonumber \\ = -\dfrac{GM}{||\vecs{r}||^3}\left[ ||\vecs{r} \left(\dfrac{d}{dt} ||\vecs{r}||\right)\vecs{r} - ||\vecs{r}||^2\vecs{v} \right] \nonumber \\ = -GM\left[ \dfrac{1}{||\vecs{r}||^2}\left( \dfrac{d}{dt} ||\vecs{r}|| \right)\vecs{r} - \dfrac{1}{||\vecs{r}||}\vecs{v} \right] \nonumber \\ = GM\left[ \dfrac{\vecs{v}}{||\vecs{r}||} -\dfrac{\vecs{r}}{||\vecs{r}||^2}\left( \dfrac{d}{dt} ||\vecs{r}|| \right) \right]. \label{Eq15} \end{align} \]

Sin embargo,

\[ \begin{align*} \dfrac{d}{dt} \dfrac{\vecs{r}}{||\vecs{r}||} = \dfrac{ \frac{d}{dt}(\vecs{r})||\vecs{r}||- \vecs{r}\frac{d}{dt}||\vecs{r}|| }{||\vecs{r}||^2} \\ = \dfrac{ \frac{d\vecs{r}}{dt} }{||\vecs{r}||} - \dfrac{\vecs{r}}{||\vecs{r}||^2}\dfrac{d}{dt}||\vecs{r} || \\ = \dfrac{\vecs{v}}{||\vecs{r}||} - \dfrac{\vecs{r}}{||\vecs{r}||^2} \dfrac{d}{dt}||\vecs{r}||. \end{align*}\]

Por lo tanto, la Ecuación\ ref {Eq15} se convierte

\[\dfrac{d \vecs{v}}{dt}\times \vecs{C}=GM\left( \dfrac{d}{dt}\dfrac{ \vecs{r}}{ || \vecs{r} ||} \right).\nonumber \]

Dado que\(\vecs{C}\) es un vector constante, podemos integrar ambos lados y obtener

\[ \vecs{v}\times\vecs{C} = GM \dfrac{ \vecs{r} }{|| \vecs{r} ||} + \vecs{D}, \nonumber \]

donde\(\vecs D\) es un vector constante. Nuestro objetivo es resolver para\(|| \vecs{r} ||\). Empecemos calculando\( \vecs{r} \cdot ( \vecs{v}\times \vecs{C}\):

\[\vecs{r} \cdot ( \vecs{v}\times \vecs{C} =GM\dfrac{||\vecs{r}||^2}{||\vecs{r}||}+ \vecs{r}\cdot\vecs{D} =GM||\vecs{r}||+\vecs{r}\cdot \vecs{D}. \nonumber \]

Sin embargo,\( \vecs{r} \cdot ( \vecs{v}\times \vecs{C})= ( \vecs{r} \times \vecs{v})\cdot \vecs{C} \), entonces

\[ ( \vecs{r} \times \vecs{v})\cdot \vecs{C} =GM||\vecs{r}|| + \vecs{r}\cdot \vecs{D}.\nonumber \]

Desde entonces\(\vecs{r}\times \vecs{v}=\vecs{C}\), tenemos

\[ ||\vecs{C}||^2 =GM||\vecs{r}|| +\vecs{r}\cdot \vecs{D}.\nonumber \]

Tenga en cuenta que\( \vecs{r} \cdot \vecs{D}=||\vecs{r}|| ||\vecs{D}||\cos \theta \), donde\(\theta\) esta el angulo entre\(\vecs{r}\) y\(\vecs{D}\). Por lo tanto,

\[ ||\vecs{C}||^2=GM||\vecs{r}||+||\vecs{r}|| ||\vecs{D}|| \cos\theta \nonumber \]

Resolviendo para\(||\vecs{r}||\),

\[ ||\vecs{r}|| = \dfrac{||\vecs{C}||^2 }{GM+||\vecs{D}||\cos\theta} = \dfrac{||\vecs{C}||^2}{GM}\left( \dfrac{1}{1+e\cos\theta} \right). \nonumber \]

donde\(e=||\vecs{D}||/GM\). Esta es la ecuación polar de una cónica con un foco en el origen, que configuramos para ser el Sol. Es una hipérbola si\(e>1\), una parábola si\(e=1\), o una elipse si\(e<1\). Dado que los planetas tienen órbitas cerradas, la única posibilidad es una elipse. No obstante, en este punto cabe mencionar que los cometas hiperbólicos sí existen. Se trata de objetos que simplemente están pasando a través del sistema solar a velocidades demasiado grandes para quedar atrapados en órbita alrededor del Sol. A medida que pasan lo suficientemente cerca del Sol, el campo gravitacional del Sol desvía la trayectoria lo suficiente para que el camino se vuelva hiperbólico.

\(\square\)

La tercera ley de movimiento planetario de Kepler puede modificarse al caso de un objeto en órbita alrededor de un objeto que no sea el Sol, como la Luna alrededor de la Tierra. En este caso, la tercera ley de Kepler se convierte en

\[P^2 = \dfrac{4\pi^2 a^3}{G(m+M)}, \label{Eq30} \]

donde m es la masa de la Luna y M es la masa de la Tierra, a representa la longitud del eje mayor de la órbita elíptica, y P representa el período.

Ejemplo\(\PageIndex{4}\): Using Kepler’s Third Law for Nonheliocentric Orbits

Dado que la masa de la Luna es\(7.35\times 10^{22}\) kg, la masa de la Tierra es\(5.97\times 10^{24}\) kg,\(G=6.67\times 10^{−11} \text{m} / \text{kg} \cdot \text{sec}^2\), y el periodo de la luna es de 27.3 días, encontremos la longitud del eje mayor de la órbita de la Luna alrededor de la Tierra.

Solución

Es importante ser congruentes con las unidades. Dado que la constante gravitacional universal contiene segundos en las unidades, también necesitamos usar segundos para el período de la Luna:

\[27.3 \; \text{days} \times \dfrac{24 \; \text{hr}}{1 \; \text{day}} \times \dfrac{3600 \; \text{esc}}{1 \; \text{hour}} =2,358,720\; \text{sec}\nonumber \]

Sustituya todos los datos en Ecuación\ ref {Eq30} y resuelva para\(a\):

\[\begin{align*} (2,358,720sec)^2 = \dfrac{4\pi^2a^3}{\left( 6.67\times 10^{-11} \frac{m}{\text{kg}\times \text{sec}^2}\right) (7.35\times 10^{22}\text{kg} + 5.97 \times 10^{24}\text{kg})} \\ 5.563 \times 10^{12} = \dfrac{ 4\pi^2a^3}{(6.67 \times 10^{-11}\text{m}^3)(6.04 \times 10^{24})} \\ (5.563 \times 10^{12})(6.67 \times 10^{-11} \text{m}^3)(6.04 \times 10^{24}) = 4\pi^2 a^3 \\ a^3 = \dfrac{2.241 \times 10^{27}}{4\pi^2}\text{m}^3 \\ a = 3.84 \times 10^8 \text{m} \\ \approx 384,000 \,\text{km}. \end{align*}\]

Análisis

Según solarsystem.nasa.gov, la distancia promedio real de la Luna a la Tierra es de 384,400 km. Esto se calcula utilizando reflectores dejados en la Luna por los astronautas de Apolo allá por la década de 1960.

Ejercicio\(\PageIndex{4}\)

Titán es la luna más grande de Saturno. La masa de Titán es aproximadamente\(1.35 \times 10^{23} kg\). La masa de Saturno es de aproximadamente\( 5.68 \times 10^{26}\) kg. Titán tarda aproximadamente 16 días en orbitar Saturno. Utilice esta información, junto con la constante de gravitación universal\(G=6.67×10^{−11} \text{m}/\text{kg} \cdot \text{sec}^2\) para estimar la distancia de Titán a Saturno.

Pista

Asegúrate de que tus unidades estén de acuerdo, luego usa la Ecuación\ ref {Eq30}.

Responder

\[a\approx 1.224 \times 10^9 \text{m}= 1,224,000 \text{km} \nonumber \]

Ejemplo\(\PageIndex{5}\): Halley’s Comet

Ahora volvemos al abridor de capítulos, que discute el movimiento del cometa Halley alrededor del Sol. La primera ley de Kepler establece que el cometa Halley sigue un camino elíptico alrededor del Sol, con el Sol como un foco de la elipse. El período del cometa Halley es de aproximadamente 76.1 años, dependiendo de lo cerca que pase por Júpiter y Saturno a medida que pase por el sistema solar exterior. Vamos a usar\(T=76.1\) años. ¿Cuál es la distancia promedio del cometa Halley y el Sol?

Solución

Usando la ecuación\(T^2=D^3\) con\(T=76.1\), obtenemos\(D^3=5791.21\), por lo que\(D\approx 17.96\) A.U. esto sale a aproximadamente\(1.67\times 10^9\) mi.

Una pregunta natural es: ¿Cuáles son las distancias máxima (afelio) y mínima (perihelio) desde el cometa Halley hasta el Sol? La excentricidad de la órbita del cometa Halley es 0.967 (Fuente: http://nssdc.gsfc.nasa.gov/planetary...cometfact.html). Recordemos que la fórmula para la excentricidad de una elipse es\(e=c/a\), donde a es la longitud del eje semimajor y c es la distancia desde el centro a cualquiera de los focos. Por lo tanto,\(0.967=c/17.96\) y\(c\approx 17.37\) A.U. restando esto de un da la distancia del perihelio\(p=a−c=17.96−17.37=0.59\) A.U. Según el Centro Nacional de Datos de Ciencias Espaciales (Fuente: http://nssdc.gsfc.nasa.gov/planetary...cometfact.html), la distancia del perihelio para el cometa Halley es de 0.587 A.U. Para calcular la distancia del afelio, agregamos

\[ P=a+c=17.96+17.37=35.33 \; \text{A.U.} \nonumber \]

Esto es aproximadamente\(3.3\times 10^9\) mi. La distancia promedio de Plutón al Sol es de 39.5 A.U. (Fuente: http://www.oarval.org/furthest.htm), por lo que parecería que Halley's Comet se queda justo dentro de la órbita de Plutón.

Navegando por un giro bancario

¿Qué tan rápido puede viajar un coche de carreras a través de un giro circular sin derrapar y chocar contra la pared? La respuesta podría depender de varios factores:

• El peso del auto;
• La fricción entre las llantas y la carretera;
• El radio del círculo;
• La “pendiente” del giro.

En este proyecto investigamos esta pregunta para las carreras de NASCAR en el Bristol Motor Speedway en Tennessee. Antes de considerar esta pista en particular, utilizamos funciones vectoriales para desarrollar las matemáticas y la física necesarias para responder preguntas como esta.

Un carro de masa\(m\) se mueve con velocidad angular constante\(\omega\) alrededor de una curva circular de radio\(R\) (Figura\(\PageIndex{9}\)). La curva está inclinada en ángulo\(\theta\). Si la altura del automóvil fuera del suelo es\(h\), entonces la posición del automóvil en el momento\(t\) viene dada por la función\(\vecs r(t)=< R\cos(\omega t),R\sin(\omega t),h>\).

Figura\(\PageIndex{9}\): Vistas de un auto de carreras que se mueve alrededor de una pista.

1. Encuentra la función\(\vecs{v}(t)\) de velocidad del auto. Mostrar que\(\vecs{v}\) es tangente a la curva circular. Esto significa que, sin una fuerza para mantener el auto en la curva, el auto se disparará fuera de él.
2. Demuestre que la velocidad del auto es\(\omega R\). Usa esto para demostrarlo\((2\pi 4)/\|\vecs{v}\|=(2\pi)/\omega \).
3. Encuentra la aceleración\(\vecs{a}\). Mostrar que este vector apunta hacia el centro del círculo y eso\(\|\vecs{a}\|=R\omega ^2\).
4. La fuerza requerida para producir este movimiento circular se llama fuerza centrípeta, y se denota\( \vecs{F}_{cent} \). Esta fuerza apunta hacia el centro del círculo (no hacia el suelo). \(\|\vecs{F}_{cent}\|=\left(m|\vecs{v}|^2 \right)/R\)Demuéstralo.

A medida que el carro se mueve alrededor de la curva, actúan sobre ella tres fuerzas: la gravedad, la fuerza ejercida por la carretera (esta fuerza es perpendicular al suelo) y la fuerza de fricción (Figura\(\PageIndex{10}\)). Debido a que describir la fuerza de fricción generada por las llantas y la carretera es compleja, utilizamos una aproximación estándar para la fuerza de fricción. Supongamos que\(\vecs{f}=\mu \vecs{N}\) para alguna constante positiva\(\mu \). La constante\(\mu\) se llama el coeficiente de fricción.

Figura\(\PageIndex{10}\): El automóvil tiene tres fuerzas que actúan sobre él: la gravedad (denotada por\(m\vecs g\)), la fuerza\(\vecs f\) de fricción y la fuerza ejercida por la carretera\(\vecs N\).

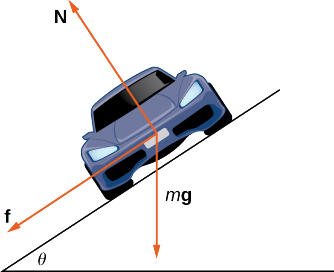
Dejar\(v_{max}\) denotar la velocidad máxima que el coche puede alcanzar a través de la curva sin derrapar. En otras palabras,\(v_{max}\) es la velocidad más rápida a la que el automóvil puede navegar el giro. Cuando el automóvil viaja a esta velocidad, la magnitud de la fuerza centrípeta es

\[\| \vecs{F}_{cent} \| = \dfrac{m(v_{max})^2}{R}. \nonumber \]

Las siguientes tres preguntas tratan de desarrollar una fórmula que relacione la velocidad\(v_{max}\) con el ángulo bancario\(\theta\).

5. \(\vecs{N} \cos\theta=m\vecs g+\vecs{f} \sin\theta\)Demuéstralo. Concluir eso\(\vecs{N}=(m\vecs g)/(\cos\theta−\mu \sin\theta)\).
6. La fuerza centrípeta es la suma de las fuerzas en dirección horizontal, ya que la fuerza centrípeta apunta hacia el centro de la curva circular. Demostrar que

   \[\vecs{F}_{cent}=\vecs{N} \sin\theta+\vecs{f}\cos\theta. \nonumber \]

   Concluir que

   \[\vecs{F}_{cent}=\dfrac{\sin\theta+\mu \cos\theta}{cos\theta−\mu \sin\theta} m\vecs g. \nonumber \]

7. \((v_{\text{max}})^2=((\sin\theta+\mu\ cos\theta)/(\cos\theta−\mu \sin\theta))gR\)Demuéstralo. Concluir que la velocidad máxima en realidad no depende de la masa del automóvil.
   Ahora que tenemos una fórmula que relaciona la velocidad máxima del automóvil y el ángulo bancario, estamos en condiciones de responder a preguntas como la planteada al inicio del proyecto.
   El Bristol Motor Speedway es una pista corta de NASCAR en Bristol, Tennessee. La pista tiene la forma aproximada que se muestra en la Figura\(\PageIndex{11}\). Cada extremo de la vía es aproximadamente semicircular, por lo que cuando los autos hacen giros están viajando a lo largo de una curva aproximadamente circular. Si un automóvil toma la vía interior y acelera a lo largo de la parte inferior de la curva 1, el automóvil viaja a lo largo de un semicírculo de radio de aproximadamente 211 pies con un ángulo de inclinación de 24°. Si el automóvil decide tomar la pista exterior y velocidades a lo largo de la parte superior de la curva 1, entonces el automóvil viaja a lo largo de un semicírculo con un ángulo de inclinación de 28°. (La pista tiene bancada de ángulo variable.)

Figura\(\PageIndex{11}\): En el Bristol Motor Speedway, Bristol, Tennessee (a), los giros tienen un radio interno de aproximadamente 211 pies y un ancho de 40 pies (b). (crédito: parte (a) foto de Raniel Diaz, Flickr)

El coeficiente de fricción para una llanta normal en condiciones secas es de aproximadamente 0.7. Por lo tanto, asumimos que el coeficiente para una llanta NASCAR en condiciones secas es de aproximadamente 0.98.

Antes de responder las siguientes preguntas, tenga en cuenta que es más fácil hacer cálculos en términos de pies y segundos, para luego convertir las respuestas a millas por hora como paso final.

8. En condiciones secas, ¿qué tan rápido puede viajar el automóvil por la parte inferior del giro sin derrapar?
9. En condiciones secas, ¿qué tan rápido puede viajar el automóvil por la parte superior del giro sin derrapar?
10. En condiciones húmedas, el coeficiente de fricción puede llegar a ser tan bajo como 0.1. Si este es el caso, ¿qué tan rápido puede viajar el automóvil por la parte inferior del giro sin derrapar?
11. Supongamos que la velocidad medida de un automóvil que va por el borde exterior del giro es de 105 mph. Estimar el coeficiente de fricción para las llantas del automóvil.

Conceptos clave

• Si\(\vecs{r}(t)\) representa la posición de un objeto en el tiempo t, entonces\(\vecs{r}'(t)\) representa la velocidad y\(\vecs{r}′′(t)\) representa la aceleración del objeto en el tiempo t. La magnitud del vector de velocidad es velocidad.
• El vector de aceleración siempre apunta hacia el lado cóncavo de la curva definida por\(\vecs{r}(t)\). Los componentes tangencial y normal de la aceleración\(a_\vecs{T}\) y\(a_\vecs{N}\) son las proyecciones del vector de aceleración sobre los vectores tangentes unitarios y normales unitarios a la curva.
• Las tres leyes del movimiento planetario de Kepler describen el movimiento de objetos en órbita alrededor del Sol. Su tercera ley puede ser modificada para describir el movimiento de objetos en órbita alrededor de otros objetos celestes también.
• Newton pudo utilizar su ley de la gravitación universal en conjunto con su segunda ley del movimiento y el cálculo para probar las tres leyes de Kepler.

Ecuaciones Clave

• Velocity\[\vecs{v}(t)=\vecs{r}′(t) \nonumber \]
• Aceleración\[\vecs{a}(t)=\vecs{v}′(t)=\vecs{r}′′(t) \nonumber \]
• Velocidad\[v(t)=||\vecs{v}(t)||=||\vecs{r}′(t)||=\dfrac{ds}{dt} \nonumber \]
• Componente tangencial de la aceleración\[a_{\vecs{T}} =\vecs{a}\cdot \vecs{T}=\dfrac{\vecs{v}\cdot \vecs{a}}{||\vecs v||} \nonumber \]
• Componente normal de aceleración\[a_{\vecs{N}}=\vecs{a}\cdot \vecs{N} = \dfrac{|| \vecs{v} \times \vecs{a} ||}{||\vecs{v}||} = \sqrt{||\vecs{a}||^2 - a_{\vecs{T}}} \nonumber \]

Glosario

vector de aceleración

la segunda derivada del vector de posición

Las leyes de Kepler del movimiento planetario

tres leyes que rigen el movimiento de planetas, asteroides y cometas en órbita alrededor del Sol

componente normal de aceleración

el coeficiente del vector normal unitario\(\vecs N\) cuando el vector de aceleración se escribe como una combinación lineal de\(\vecs T\) y\(\vecs N\)

movimiento de proyectil

movimiento de un objeto con una velocidad inicial pero ninguna fuerza que actúe sobre él distinta de la gravedad

componente tangencial de la aceleración

el coeficiente del vector tangente unitario\(\vecs T\) cuando el vector de aceleración se escribe como una combinación lineal de\(\vecs T\) y\(\vecs N\)

vector de velocidad

la derivada del vector de posición

Colaboradores y Atribuciones

• Template:ContribOpenStaxCalc
• Edited by Paul Seeburger
  Paul Seeburger added finding point \((1, 2)\) when \(t=1\) in Example \(\PageIndex{1}\).
  He also created Figure \(\PageIndex{1}\).