13.4E: Ejercicios para la Sección 13.4

1) Dado\(\vecs r(t)=(3t^2−2)\,\hat{\mathbf{i}}+(2t−\sin t)\,\hat{\mathbf{j}}\),

a. encontrar la velocidad de una partícula que se mueve a lo largo de esta curva.

b. encontrar la aceleración de una partícula que se mueve a lo largo de esta curva.

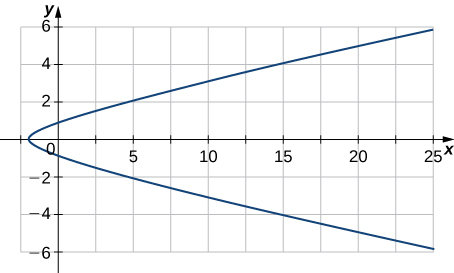
Contestar

a.\(\vecs v(t)=6t\,\hat{\mathbf{i}}+(2−\cos t)\,\hat{\mathbf{i}}\)
b.\(\vecs a(t)=6\,\hat{\mathbf{i}}+\sin t\,\hat{\mathbf{i}}\)

En las preguntas 2 a 5, dada la función de posición, encuentra la velocidad, la aceleración y la velocidad en términos del parámetro\(t\).

2)\(\vecs r(t)=e^{−t}\,\hat{\mathbf{i}}+t^2\,\hat{\mathbf{j}}+\tan t\,\hat{\mathbf{k}}\)

3)\(\vecs r(t)=⟨3\cos t,\,3\sin t,\,t^2⟩\)

Contestar

\(\vecs v(t)=-3\sin t\,\hat{\mathbf{i}}+3\cos t\,\hat{\mathbf{j}}+2t\,\hat{\mathbf{k}}\)
\(\vecs a(t)=-3\cos t\,\hat{\mathbf{i}}-3\sin t\,\hat{\mathbf{j}}+2\,\hat{\mathbf{k}}\)
\(\text{Speed}(t) = \|\vecs v(t)\| = \sqrt{9 + 4t^2}\)

4)\(\vecs r(t)=t^5\,\hat{\mathbf{i}}+(3t^2+2t- 5)\,\hat{\mathbf{j}}+(3t-1)\,\hat{\mathbf{k}}\)

5)\(\vecs r(t)=2\cos t\,\hat{\mathbf{j}}+3\sin t\,\hat{\mathbf{k}}\). El gráfico se muestra aquí:

Contestar

\(\vecs v(t)=-2\sin t\,\hat{\mathbf{j}}+3\cos t\,\hat{\mathbf{k}}\)
\(\vecs a(t)=-2\cos t\,\hat{\mathbf{j}}-3\sin t\,\hat{\mathbf{k}}\)
\(\text{Speed}(t) = \|\vecs v(t)\| = \sqrt{4\sin^2 t+9\cos^2 t}=\sqrt{4+5\cos^2 t}\)

En las preguntas 6 a 8, encuentra la velocidad, aceleración y velocidad de una partícula con la función de posición dada.

6)\(\vecs r(t)=⟨t^2−1,t⟩\)

7)\(\vecs r(t)=⟨e^t,e^{−t}⟩\)

Contestar

\(\vecs v(t)=⟨e^t,−e^{−t}⟩\),
\(\vecs a(t)=⟨e^t, e^{−t}⟩,\)
\( \|\vecs v(t)\| = \sqrt{e^{2t}+e^{−2t}}\)

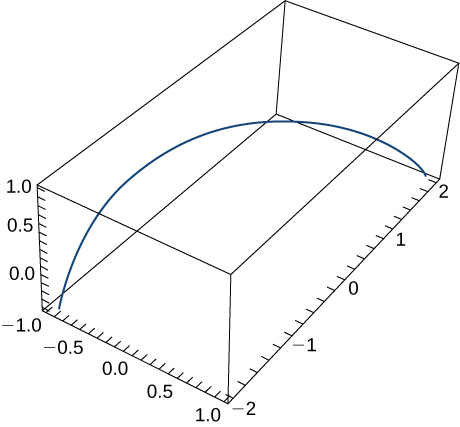
8)\(\vecs r(t)=⟨\sin t,t,\cos t⟩\). El gráfico se muestra aquí:

9) La función de posición de un objeto viene dada por\(\vecs r(t)=⟨t^2,5t,t^2−16t⟩\). ¿A qué hora es mínima la velocidad?

Contestar

\(t = 4\)

10) Dejar\(\vecs r(t)=r\cosh(ωt)\,\hat{\mathbf{i}}+r\sinh(ωt)\,\hat{\mathbf{j}}\). Encuentra los vectores de velocidad y aceleración y muestra que la aceleración es proporcional a\(\vecs r(t)\).

11) Considerar el movimiento de un punto en la circunferencia de un círculo rodante. A medida que el círculo rueda, genera el cicloide\(\vecs r(t)=(ωt−\sin(ωt))\,\hat{\mathbf{i}}+(1−\cos(ωt))\,\hat{\mathbf{j}}\), donde\(\omega\) está la velocidad angular del círculo y\(b\) es el radio del círculo:

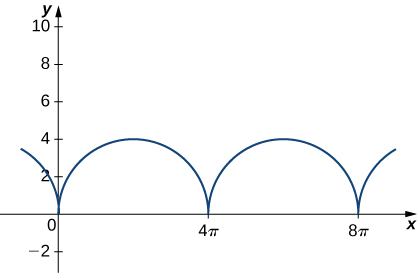
Encuentre las ecuaciones para la velocidad, aceleración y velocidad de la partícula en cualquier momento.

Contestar

\(\vecs v(t)=(ω−ω\cos(ωt))\,\hat{\mathbf{i}}+(ω\sin(ωt))\,\hat{\mathbf{j}}\)
\(\vecs a(t)=(ω^2\sin(ωt))\,\hat{\mathbf{i}}+(ω^2\cos(ωt))\,\hat{\mathbf{j}}\)
\ (\ begin {align*}\ text {speed} (t) &=\ sqrt {(ω−ω\ cos (ωt)) ^2 + (ω\ sin (ωt)) ^2}\\
&=\ sqrt {ω^2 - 2ω^2\ cos (ωt) + ω^2\ cos^2 (ωt) + ω^2\ sin^2 (ωt)}\\
&=\ sqrt {2ω^2 (1 -\ cos (ωt))}\ end {alinear*}\)

12) Una persona en un ala delta está en espiral hacia arriba como resultado del rápido ascenso del aire en un camino que tiene vector de posición\(\vecs r(t)=(3\cos t)\,\hat{\mathbf{i}}+(3\sin t)\,\hat{\mathbf{j}}+t^2\,\hat{\mathbf{k}}\). El camino es similar al de una hélice, aunque no es una hélice. El gráfico se muestra aquí:

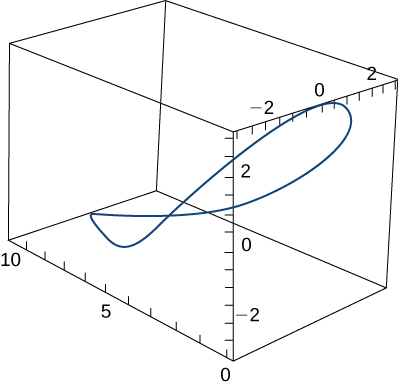
Encuentra las siguientes cantidades:

a. Los vectores de velocidad y aceleración

b. La velocidad del planeador en cualquier momento

Contestar

\(\|\vecs v(t)\|=\sqrt{9+4t^2}\)

c. Los tiempos, en su caso, en los que la aceleración del planeador es ortogonal a su velocidad

13) Dado que\(\vecs r(t)=⟨e^{−5t}\sin t,\, e^{−5t}\cos t,\, 4e^{−5t}⟩\) es el vector de posición de una partícula en movimiento, encuentre las siguientes cantidades:

a. La velocidad de la partícula

Contestar

\(\vecs v(t)=⟨e^{−5t}(\cos t−5\sin t),\, −e^{−5t}(\sin t+5\cos t),\, −20e^{−5t}⟩\)

b. La velocidad de la partícula

c. La aceleración de la partícula

Contestar

\(\vecs a(t)=⟨e^{−5t}(−\sin t−5\cos t)−5e^{−5t}(\cos t−5\sin t), \; −e^{−5t}(\cos t−5\sin t)+5e^{−5t}(\sin t+5\cos t),\; 100e^{−5t}⟩\)

14) Encuentra la velocidad máxima de un punto en la circunferencia de una llanta de automóvil de radio\(1\) ft cuando el automóvil viaja a\(55\) mph.

15) Encontrar la función de posición valorada por vector\(\vecs r(t)\), dado que\(\vecs a(t)=\hat{\mathbf{i}}+e^t \,\hat{\mathbf{j}}, \quad \vecs v(0)=2\,\hat{\mathbf{j}}\), y\(\vecs r(0)=2\,\hat{\mathbf{i}}\).

16) Encontrar\(\vecs r(t)\) dado eso\(\vecs a(t)=−32\,\hat{\mathbf{j}}, \vecs v(0)=600\sqrt{3} \,\hat{\mathbf{i}}+600\,\hat{\mathbf{j}}\), y\(\vecs r(0)=\vecs 0\).

17) La aceleración de un objeto viene dada por\(\vecs a(t)=t\,\hat{\mathbf{j}}+t\,\hat{\mathbf{k}}\). La velocidad en\(t=1\) segundos es\(\vecs v(1)=5\,\hat{\mathbf{j}}\) y la posición del objeto en\(t=1\) seg es\(\vecs r(1)=0\,\hat{\mathbf{i}}+0\,\hat{\mathbf{j}}+0\,\hat{\mathbf{k}}\). Encuentra la posición del objeto en cualquier momento.

Contestar

\(\vecs r(t)=0\,\hat{\mathbf{i}}+\left(\frac{1}{6}t^3+4.5t−\frac{14}{3}\right)\,\hat{\mathbf{j}}+\left(\frac{1}{6}t^3−\frac{1}{2}t+\frac{1}{3}\right)\,\hat{\mathbf{k}}\)

Movimiento del Proyectil

18) Un proyectil es disparado en el aire desde el nivel del suelo con una velocidad inicial de\(500\) m/seg en un ángulo de 60° con la horizontal.

a.- ¿A qué hora alcanza la altura máxima el proyectil?

Contestar

\(44.185\)sec

b. ¿Cuál es la altura máxima aproximada del proyectil?

c. ¿En qué momento se alcanza el alcance máximo del proyectil?

Contestar

\(t=88.37\)sec

d. ¿Cuál es el rango máximo?

e. ¿Cuál es el tiempo total de vuelo del proyectil?

Contestar

\(t=88.37\)sec

19) Se dispara un proyectil a una altura de\(1.5\) m sobre el suelo con una velocidad inicial de\(100\) m/seg y en un ángulo de 30° por encima de la horizontal. Utilice esta información para responder a las siguientes preguntas:

a. Determinar la altura máxima del proyectil.

b. Determinar el alcance del proyectil.

Contestar

El rango es de aproximadamente\(886.29\) m.

20) Una pelota de golf es golpeada en una dirección horizontal desde el borde superior de un edificio que mide 100 pies de altura. ¿Qué tan rápido se debe lanzar la pelota para aterrizar a\(450\) pies de distancia?

21) Un proyectil se dispara desde el nivel del suelo en un ángulo de 8° con la horizontal. El proyectil debe tener un alcance de\(50\) m. Encontrar la velocidad mínima (velocidad) necesaria para lograr este rango.

Contestar

\(v=42.16\)m/seg

22) Demostrar que un objeto que se mueve en línea recta a una velocidad constante tiene una aceleración de cero.

Encontrar componentes de aceleración y leyes de Kepler

23) Encuentra los componentes tangenciales y normales de aceleración para\(\vecs r(t)=t^2\,\hat{\mathbf{i}}+2t \,\hat{\mathbf{j}}\) cuando\(t=1\).

Contestar

\(a_\vecs{T}=\sqrt{2}, \quad a_\vecs{N}=\sqrt{2}\)

En las preguntas 24 a 30, encuentra los componentes tangenciales y normales de la aceleración.

24)\(\vecs r(t)=⟨\cos(2t),\,\sin(2t),1⟩\)

25)\(\vecs r(t)=⟨e^t \cos t,\,e^t\sin t,\,e^t⟩\). El gráfico se muestra aquí:

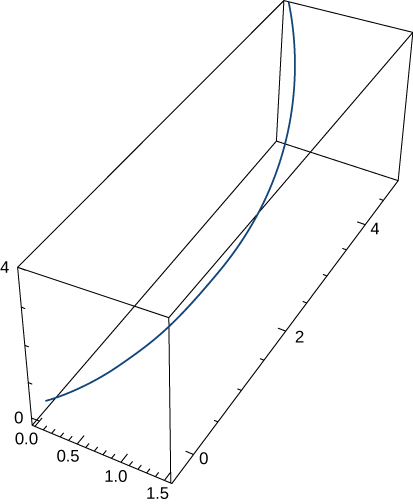
Contestar

\(a_\vecs{T}=\sqrt{3}e^t, \quad a_\vecs{N}=\sqrt{2}e^t\)

26)\(\vecs r(t)=⟨\frac{2}{3}(1+t)^{3/2}, \,\frac{2}{3}(1-t)^{3/2},\,\sqrt{2}t⟩\)

27)\(\vecs r(t)=\left\langle 2t,\,t^2,\,\dfrac{t^3}{3}\right\rangle\)

Contestar

\(a_\vecs{T}=2t, \quad a_\vecs{N}=2\)

28)\(\vecs r(t)=t^2\,\hat{\mathbf{i}}+t^2\,\hat{\mathbf{j}}+t^3\,\hat{\mathbf{k}}\)

29)\(\vecs r(t)=⟨6t,\,3t^2,\,2t^3⟩\)

Contestar

\(a_\vecs{T}=\dfrac{6t +12t^3}{\sqrt{1+t^2+t^4}}, \quad a_\vecs{N}=6\sqrt{\dfrac{1+4t^2+t^4}{1+t^2+t^4}}\)

30)\(\vecs r(t)=3\cos(2πt)\,\hat{\mathbf{i}}+3\sin(2πt)\,\hat{\mathbf{j}}\)

Contestar

\(a_\vecs{T}=0, \quad a_\vecs{N}=12\pi^2\)

31) Encontrar los componentes tangenciales y normales de aceleración para\(\vecs r(t)=a\cos(ωt)\,\hat{\mathbf{i}}+b\sin(ωt)\,\hat{\mathbf{j}}\) at\(t=0\).

Contestar

\(a_\vecs{T}=0, \quad a_\vecs{N}=aω^2\)

32) Supongamos que la función de posición para un objeto en tres dimensiones viene dada por la ecuación\(\vecs r(t)=t\cos(t)\,\hat{\mathbf{i}}+t\sin(t)\,\hat{\mathbf{j}}+3t\,\hat{\mathbf{k}}\).

a. Demostrar que la partícula se mueve sobre un cono circular.

b. encontrar el ángulo entre los vectores de velocidad y aceleración cuando\(t=1.5\).

c. Encontrar los componentes tangenciales y normales de la aceleración cuando\(t=1.5\).

Contestar

c.\(a_\vecs{T}=0.43\,\text{m/sec}^2, \quad a_\vecs{N}=2.46\,\text{m/sec}^2\)

33) La fuerza sobre una partícula viene dada por\(\vecs f(t)=(\cos t)\,\hat{\mathbf{i}}+(\sin t)\,\hat{\mathbf{j}}\). La partícula se localiza en el punto\((c,0)\) en\(t=0\). La velocidad inicial de la partícula viene dada por\(\vecs v(0)=v_0\,\hat{\mathbf{j}}\). Encuentra el camino de la partícula de masa\(m\). (Recordar,\(\vecs F=m\vecs a\).)

Contestar

\(\vecs r(t)=\left(\dfrac{-\cos t}{m}+c+\frac{1}{m}\right)\,\hat{\mathbf{i}}+\left(\dfrac{−\sin t}{m}+\left(v_0+\frac{1}{m}\right)t\right)\,\hat{\mathbf{j}}\)

34) Un automóvil que pesa\(2700\) lb hace un giro en una carretera plana mientras viaja a\(56\) pies/seg. Si el radio de giro es\(70\) ft, ¿cuál es la fuerza de fricción requerida para evitar que el automóvil derrape?

35) Usando las leyes de Kepler, se puede demostrar que\(v_0=\sqrt{\dfrac{2GM}{r_0}}\) es la velocidad mínima necesaria cuando\(\theta=0\) para que un objeto se escape de la tracción de una fuerza central resultante de la masa\(M\). Usa este resultado para encontrar la velocidad mínima cuando\(\theta=0\) para que una cápsula espacial escape de la atracción gravitacional de la Tierra si la sonda se encuentra a una altitud de\(300\) km sobre la superficie de la Tierra.

Contestar

\(10.94\)km/seg

36) Encuentra el tiempo en años que tarda el planeta enano Plutón en hacer una órbita alrededor del Sol dado que\(a=39.5\) A.U.

Colaboradores

Template:ContribOpenStaxCalc