16.1E: Ejercicios para la Sección 16.1
- Page ID
- 116774
1. El dominio del campo vectorial\(\vecs{F}=\vecs{F}(x,y)\) es un conjunto de puntos\((x,y)\) en un plano, y el rango de\(\vecs F\) es un conjunto de lo que en el plano?
- Contestar
- Vectores
Para los ejercicios 2 - 4, determinar si la afirmación es verdadera o falsa.
2. \(\vecs{F}=⟨3x^2,1⟩\)El campo vectorial es un campo degradado para ambos\(ϕ_1(x,y)=x^3+y\) y\(ϕ_2(x,y)=y+x^3+100.\)
3. \(\vecs{F}=\dfrac{⟨y,x⟩}{\sqrt{x^2+y^2}}\)El campo vectorial es constante en dirección y magnitud en un círculo unitario.
- Contestar
- Falso
4. \(\vecs{F}=\dfrac{⟨y,x⟩}{\sqrt{x^2+y^2}}\)El campo vectorial no es un campo radial ni un campo de rotación.
Para los ejercicios 5 - 13, describa cada campo vectorial dibujando algunos de sus vectores.
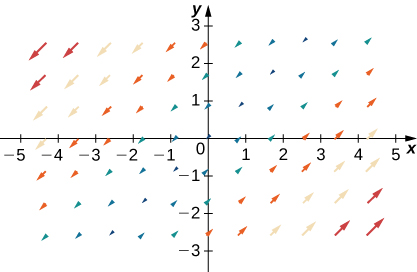
5. [T]\(\vecs{F}(x,y)=x\,\hat{\mathbf i}+y\,\hat{\mathbf j}\)
- Contestar
-
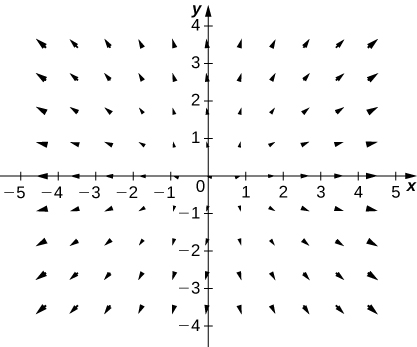
6. [T]\(\vecs{F}(x,y)=−y\,\hat{\mathbf i}+x\,\hat{\mathbf j}\)
7. [T]\(\vecs{F}(x,y)=x\,\hat{\mathbf i}−y\,\hat{\mathbf j}\)
- Contestar
-
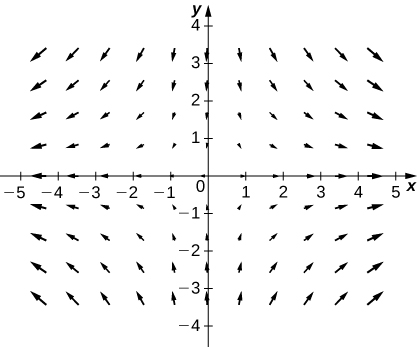
8. [T]\(\vecs{F}(x,y)=\,\hat{\mathbf i}+\,\hat{\mathbf j}\)
9. [T]\(\vecs{F}(x,y)=2x\,\hat{\mathbf i}+3y\,\hat{\mathbf j}\)
- Contestar
-
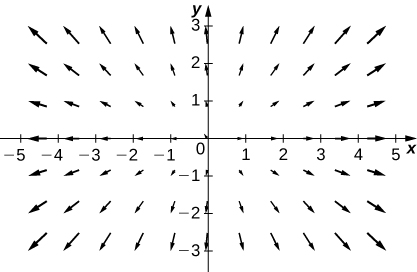
10. [T] \(\vecs{F}(x,y)=3\,\hat{\mathbf i}+x\,\hat{\mathbf j}\)
11. [T]\(\vecs{F}(x,y)=y\,\hat{\mathbf i}+\sin x\,\hat{\mathbf j}\)
- Contestar
-
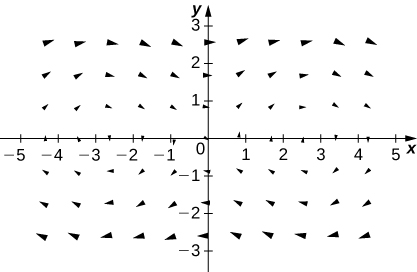
12. [T]\(\vecs F(x,y,z)=x\,\hat{\mathbf i}+y\,\hat{\mathbf j}+z\,\hat{\mathbf k}\)
13. [T]\(\vecs F(x,y,z)=2x\,\hat{\mathbf i}−2y\,\hat{\mathbf j}−2z\,\hat{\mathbf k}\)
- Contestar
-
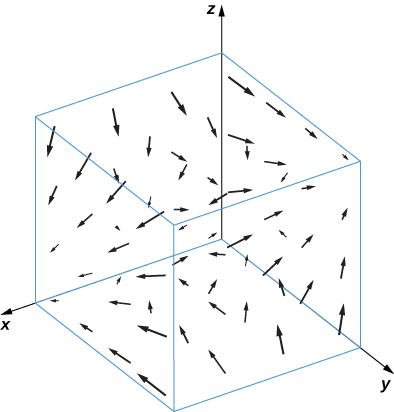
14. [T]\(\vecs F(x,y,z)=yz\,\hat{\mathbf i}−xz\,\hat{\mathbf j}\)
Para los ejercicios 15 - 20, encuentra el campo vectorial de gradiente de cada función\(f\).
15. \(f(x,y)=x\sin y+\cos y\)
- Contestar
- \(\vecs{F}(x,y)=\sin(y)\,\hat{\mathbf i}+(x\cos y−\sin y)\,\hat{\mathbf j}\)
16. \(f(x,y,z)=ze^{−xy}\)
17. \(f(x,y,z)=x^2y+xy+y^2z\)
- Contestar
- \(\vecs F(x,y,z)=(2xy+y)\,\hat{\mathbf i}+(x^2+x+2yz)\,\hat{\mathbf j}+y^2\,\hat{\mathbf k}\)
18. \(f(x,y)=x^2\sin(5y)\)
19. \(f(x,y)=\ln(1+x^2+2y^2)\)
- Contestar
- \(\vecs{F}(x,y)=\dfrac{2x}{1+x^2+2y^2}\,\hat{\mathbf i}+\dfrac{4y}{1+x^2+2y^2}\,\hat{\mathbf j}\)
20. \(f(x,y,z)=x\cos\left(\frac{y}{z}\right)\)
21. ¿Qué es el campo vectorial\(\vecs{F}(x,y)\) con un valor\((x,y)\) que es de longitud unitaria y apunta hacia\((1,0)\)?
- Contestar
- \(\vecs{F}(x,y)=\dfrac{(1−x)\,\hat{\mathbf i}−y\,\hat{\mathbf j}}{\sqrt{(1−x)^2+y^2}}\)
Para los ejercicios 22 - 24, escriba fórmulas para los campos vectoriales con las propiedades dadas.
22. Todos los vectores son paralelos al\(x\) eje -y todos los vectores en una línea vertical tienen la misma magnitud.
23. Todos los vectores apuntan hacia el origen y tienen longitud constante.
- Contestar
- \(\vecs{F}(x,y)=\dfrac{(y\,\hat{\mathbf i}−x\,\hat{\mathbf j})}{\sqrt{x^2+y^2}}\)
24. Todos los vectores son de longitud unitaria y son perpendiculares al vector de posición en ese punto.
25. Dar una fórmula\(\vecs{F}(x,y)=M(x,y)\,\hat{\mathbf i}+N(x,y)\,\hat{\mathbf j}\) para el campo vectorial en un plano que tenga las propiedades que\(\vecs{F}=\vecs 0\) en\((0,0)\) y que en cualquier otro punto\((a,b), \vecs F\) es tangente al círculo\(x^2+y^2=a^2+b^2\) y apunta en el sentido de las agujas del reloj con magnitud\(\|\vecs F\|=\sqrt{a^2+b^2}\).
- Contestar
- \(\vecs{F}(x,y)=y\,\hat{\mathbf i}−x\,\hat{\mathbf j}\)
26. ¿El campo vectorial es\(\vecs{F}(x,y)=(P(x,y),Q(x,y))=(\sin x+y)\,\hat{\mathbf i}+(\cos y+x)\,\hat{\mathbf j}\) un campo degradado?
27. Encuentra una fórmula para el campo vectorial\(\vecs{F}(x,y)=M(x,y)\,\hat{\mathbf i}+N(x,y)\,\hat{\mathbf j}\) dado el hecho de que para todos los\(\vecs F\) puntos\((x,y)\), apunta hacia el origen y\(\|\vecs F\|=\dfrac{10}{x^2+y^2}\).
- Contestar
- \(\vecs{F}(x,y)=\dfrac{−10}{(x^2+y^2)^{3/2}}(x\,\hat{\mathbf i}+y\,\hat{\mathbf j})\)
Para los ejercicios 28 - 29, supongamos que un campo eléctrico en el\(xy\) plano causado por una línea infinita de carga a lo largo del\(x\) eje es un campo de gradiente con función potencial\(V(x,y)=c\ln\left(\frac{r_0}{\sqrt{x^2+y^2}}\right)\), donde\(c>0\) es una constante y\(r_0\) es una distancia de referencia a la que el potencial se supone que es cero.
28. Encuentre los componentes del campo eléctrico en las\(y\) direcciones\(x\) - y -donde\(\vecs E(x,y)=−\vecs ∇V(x,y).\)
29. Mostrar que el campo eléctrico en un punto en el\(xy\) plano -se dirige hacia afuera desde el origen y tiene magnitud\(\|\vecs E\|=\dfrac{c}{r}\), donde\(r=\sqrt{x^2+y^2}\).
- Contestar
- \(\|\vecs E\|=\dfrac{c}{|r|^2}r=\dfrac{c}{|r|}\dfrac{r}{|r|}\)
Una línea de flujo (o aerodinámico) de un campo vectorial\(\vecs F\) es una curva\(\vecs r(t)\) tal que\(d\vecs{r}/dt=\vecs F(\vecs r(t))\). Si\(\vecs F\) representa el campo de velocidad de una partícula en movimiento, entonces las líneas de flujo son trayectorias tomadas por la partícula. Por lo tanto, las líneas de flujo son tangentes al campo vectorial.
Para los ejercicios 30 y 31, mostrar que la curva dada\(\vecs c(t)\) es una línea de flujo del campo vectorial de velocidad dado\(\vecs F(x,y,z)\).
30. \(\vecs c(t)=⟨ e^{2t},\ln|t|,\frac{1}{t} ⟩,\,t≠0;\quad \vecs F(x,y,z)=⟨2x,z,−z^2⟩\)
31. \(\vecs c(t)=⟨ \sin t,\cos t,e^t⟩;\quad \vecs F(x,y,z) =〈y,−x,z〉\)
- Contestar
- \(\vecs c′(t)=⟨ \cos t,−\sin t,e^{−t}⟩=\vecs F(\vecs c(t))\)
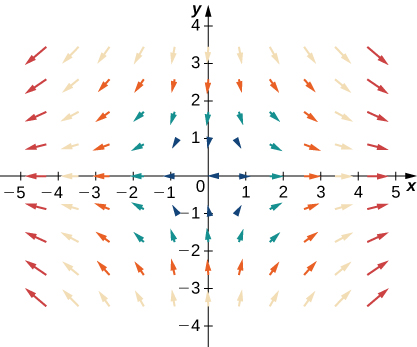
Para los ejercicios 32 - 34, let\(\vecs{F}=x\,\hat{\mathbf i}+y\,\hat{\mathbf j}\),\(\vecs G=−y\,\hat{\mathbf i}+x\,\hat{\mathbf j}\), y\(\vecs H=x\,\hat{\mathbf i}−y\,\hat{\mathbf j}\). \(\vecs F\)Coinciden\(\vecs G\),, y\(\vecs H\) con sus gráficas.
32.
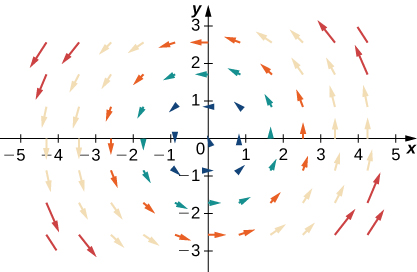
33.
- Contestar
- \(\vecs H\)
34.
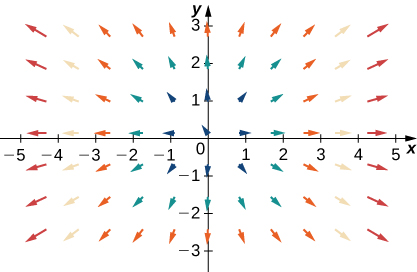
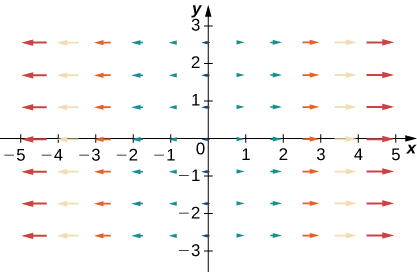
Para los ejercicios 35 - 38, let\(\vecs{F}=x\,\hat{\mathbf i}+y\,\hat{\mathbf j}\),\(\vecs G=−y\,\hat{\mathbf i}+x\,\hat{\mathbf j}\), y\(\vecs H=−x\,\hat{\mathbf i}+y\,\hat{\mathbf j}\). Haga coincidir los campos vectoriales con sus gráficas en (I) − (IV).
- \(\vecs F+\vecs G\)
- \(\vecs F+\vecs H\)
- \(\vecs G+\vecs H\)
- \(−\vecs F+\vecs G\)
35.
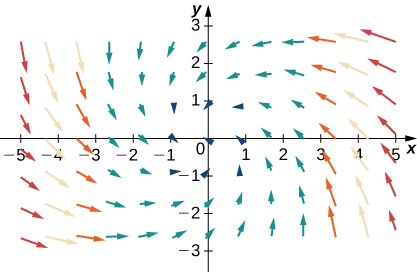
- Contestar
- d.\(−\vecs F+\vecs G\)
36.
37.
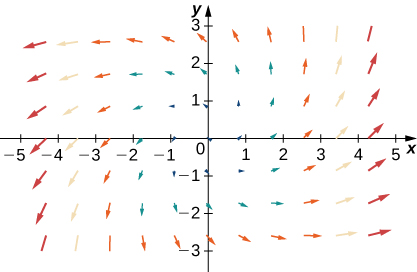
- Contestar
- a.\(\vecs F+\vecs G\)
38.