16.2: Integrales de línea

Objetivos de aprendizaje

• Calcular una línea escalar integral a lo largo de una curva.
• Calcular una integral de línea vectorial a lo largo de una curva orientada en el espacio.
• Utilice una integral de línea para calcular el trabajo realizado al mover un objeto a lo largo de una curva en un campo vectorial.
• Describir el flujo y la circulación de un campo vectorial.

Estamos familiarizados con integrales de variable única de la forma\(\displaystyle \int_{a}^{b}f(x)\,dx\), donde el dominio de integración es un intervalo\([a,b]\). Tal intervalo puede pensarse como una curva en el\(xy\) plano, ya que el intervalo define un segmento de línea con puntos finales\((a,0)\) y\((b,0)\) —en otras palabras, un segmento de línea ubicado en el\(x\) eje -eje. Supongamos que queremos integrar sobre cualquier curva en el plano, no solo sobre un segmento de línea en el\(x\) eje -eje. Tal tarea requiere de un nuevo tipo de integral, llamado integral de línea.

Las integrales de línea tienen muchas aplicaciones para ingeniería y física. También nos permiten hacer varias generalizaciones útiles del Teorema Fundamental del Cálculo. Y, están estrechamente conectados con las propiedades de los campos vectoriales, como veremos.

Integrales de Línea Escalar

Una integral de línea nos da la capacidad de integrar funciones multivariables y campos vectoriales sobre curvas arbitrarias en un plano o en el espacio. Hay dos tipos de integrales de línea: integrales de línea escalares e integrales de línea vectorial. Las integrales de línea escalar son integrales de una función escalar sobre una curva en un plano o en el espacio. Las integrales de línea vectorial son integrales de un campo vectorial sobre una curva en un plano o en el espacio. Veamos primero las integrales de línea escalar.

Una integral de línea escalar se define tal como se define una integral de variable única, excepto que para una integral de línea escalar, el integrando es una función de más de una variable y el dominio de integración es una curva en un plano o en el espacio, a diferencia de una curva en el\(x\) eje.

Para una integral de línea escalar, dejamos\(C\) ser una curva suave en un plano o en el espacio y dejamos que ff sea una función con un dominio que incluya\(C\). Cortamos la curva en trozos pequeños. Para cada pieza, elegimos punto\(P\) en esa pieza y evaluamos\(f\) en\(P\). (Podemos hacer esto porque todos los puntos en la curva están en el dominio de\(f\).) Multiplicamos\(f(P)\) por la longitud del arco de la pieza\(\Delta s\), agregamos el producto\(f(P)\Delta s\) sobre todas las piezas, y luego dejamos que la longitud del arco de las piezas se encoja a cero tomando un límite. El resultado es la línea escalar integral de la función sobre la curva.

Para una descripción formal de una integral de línea escalar, dejar\(C\) ser una curva suave en el espacio dada por la parametrización\(\vecs r(t)=⟨x(t),y(t),z(t)⟩\),\(a≤t≤b\). Dejar\(f(x,y,z)\) ser una función con un dominio que incluya curva\(C\). Para definir la línea integral de la función\(f\) sobre\(C\), comenzamos como comienzan la mayoría de las definiciones de una integral: cortamos la curva en trozos pequeños. Partición del intervalo de parámetros\([a,b]\) en\(n\) subintervalos\([t_{i−l},t_i]\) de igual ancho para\(1≤i≤n\), donde\(t_0=a\) y\(t_n=b\) (Figura\(\PageIndex{1}\)). Dejar\(t_{i}^*\) ser un valor en el\(i^{th}\) intervalo\([t_{i−l},t_i]\). Denotar los puntos finales de\(\vecs r(t_0)\),\(\vecs r(t_1)\),...,\(\vecs r(t_n)\) por\(P_0\),...,\(P_n\). Los puntos P _i dividen\(C\) la curva en\(n\) pedazos\(C_1\)\(C_2\),\(C_n\),..., con longitudes\(\Delta s_1\)\(\Delta s_2\),,...\(\Delta s_n\), respectivamente. Dejar\(P_{i}^*\) denotar el punto final de\(\vecs r(t_{i}^*)\) for\(1≤i≤n\). Ahora, evaluamos la función\(f\) en el punto\(P_{i}^*\) para\(1≤i≤n\). Tenga en cuenta que\(P_{i}^*\) está en pieza\(C_1\), y por lo tanto\(P_{i}^*\) está en el dominio de\(f\). Multiplique\(f(P_{i}^*)\) por la longitud\(\Delta s_1\) de\(C_1\), lo que da el área de la “hoja” con base\(C_1\), y altura\(f(P_{i}^{*})\). Esto es análogo al uso de rectángulos para aproximar el área en una integral de una sola variable. Ahora, formamos la suma\(\displaystyle \sum_{i=1}^{n} f(P_{i}^{*})\,\Delta s_i\).

Figura\(\PageIndex{1}\): La curva se\(C\) ha dividido en n piezas, y se ha elegido un punto dentro de cada pieza.

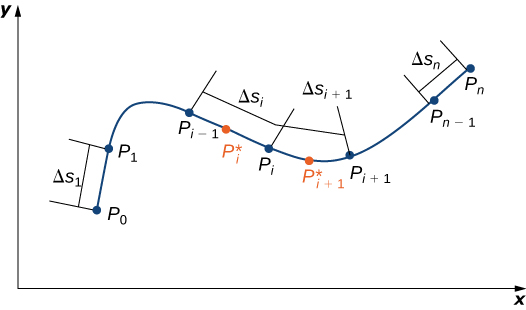
Obsérvese la similitud de esta suma frente a una suma de Riemann; de hecho, esta definición es una generalización de una suma de Riemann a curvas arbitrarias en el espacio. Al igual que con las sumas e integrales de forma de Riemann\(\displaystyle \int_{a}^{b}g(x)\,dx\), definimos una integral dejando que el ancho de las piezas de la curva se encoja a cero tomando un límite. El resultado es la línea escalar integral de\(f\) lo largo\(C\).

Es posible que haya notado una diferencia entre esta definición de una integral de línea escalar y una integral de una sola variable. En esta definición, las longitudes de arco\(\Delta s_1\)\(\Delta s_2\),,...,\(\Delta s_n\) no son necesariamente las mismas; en la definición de integral de una sola variable, la curva en el\(x\) eje -se divide en trozos de igual longitud. Esta diferencia no tiene ningún efecto en el límite. A medida que reducimos las longitudes del arco a cero, sus valores se acercan lo suficiente como para que cualquier pequeña diferencia se vuelva irrelevante.

DEFINICIÓN: Línea Escalar Integral

Dejar\(f\) ser una función con un dominio que incluya la curva suave\(C\) que es parametrizada por\(\vecs r(t)=⟨x(t),y(t),z(t)⟩\),\(a≤t≤b\). La línea escalar integral de\(f\) lo largo\(C\) es

\[\int_C f(x,y,z) \,ds=\lim_{n\to\infty}\sum_{i=1}^{n}f(P_{i}^{*})\,\Delta s_i \label{eq12a} \]

si este límite existe (\(t_i ^{*}\)y\(\Delta s_i\) se definen como en los párrafos anteriores). Si\(C\) es una curva plana, entonces se\(C\) puede representar por las ecuaciones paramétricas\(x=x(t)\),\(y=y(t)\), y\(a≤t≤b\). Si\(C\) es suave y\(f(x,y)\) es una función de dos variables, entonces la integral de línea escalar de\(f\) lo largo\(C\) se define de manera similar como

\[\int_C f(x,y) \,ds=\lim_{n\to\infty}\sum_{i=1}^{n} f(P_{i}^{*})\,\Delta s_i, \label{eq13} \]

si existe este límite.

Si\(f\) es una función continua en una curva suave\(C\), entonces\(\displaystyle \int_C f \,ds\) siempre existe. Ya que\(\displaystyle \int_C f \,ds\) se define como un límite de sumas de Riemann, la continuidad de\(f\) es suficiente para garantizar la existencia del límite, así como la integral\(\displaystyle \int_{a}^{b}g(x)\,dx\) existe si\(g\) es continua sobre\([a,b]\).

Antes de ver cómo calcular una integral de línea, necesitamos examinar la geometría capturada por estas integrales. Supongamos que\(f(x,y)≥0\) para todos los puntos\((x,y)\) en una curva plana lisa\(C\). Imagínese tomando curva\(C\) y proyectándola “hacia arriba” a la superficie definida por\(f(x,y)\), creando así una nueva curva\(C′\) que se encuentra en la gráfica de\(f(x,y)\) (Figura\(\PageIndex{2}\)). Ahora dejamos caer una “hoja” de\(C′\) abajo al\(xy\) -avión. El área de esta hoja es\(\displaystyle \int_C f(x,y)ds\). Si\(f(x,y)≤0\) para algunos puntos en\(C\), entonces el valor de\(\displaystyle \int_C f(x,y)\,ds\) es el área por encima del\(xy\) plano menos el área por debajo del\(xy\) plano. (Obsérvese la similitud con las integrales de la forma\(\displaystyle \int_{a}^{b}g(x)\,dx\).)

Figura\(\PageIndex{2}\): El área de la lámina azul es\(\displaystyle \int_C f(x,y)\,ds\).

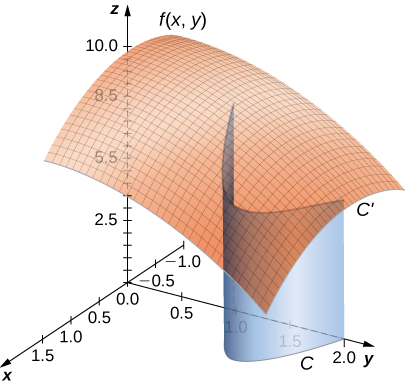
A partir de esta geometría, podemos ver que la integral de línea\(\displaystyle \int_C f(x,y)\,ds\) no depende de la parametrización\(\vecs r(t)\) de\(C\). Siempre y cuando la curva sea atravesada exactamente una vez por la parametrización, el área de la hoja formada por la función y la curva es la misma. Este mismo tipo de argumento geométrico puede extenderse para mostrar que la integral de línea de una función de tres variables sobre una curva en el espacio no depende de la parametrización de la curva.

Ejemplo\(\PageIndex{1}\): ​​​​​​Finding the Value of a Line Integral

Encuentra el valor de integral\(\displaystyle \int_C 2\,ds\), donde\(C\) está la mitad superior del círculo unitario.

Solución

El integrand es\(f(x,y)=2\). En la figura se\(\PageIndex{3}\) muestra la gráfica de\(f(x,y)=2\) la curva C y la lámina formada por ellas. Observe que esta hoja tiene la misma área que un rectángulo con ancho\(\pi\) y largo\(2\). Por lo tanto,\(\displaystyle \int_C 2 \,ds=2\pi\,\text{units}^2\).

Figura\(\PageIndex{3}\): La lámina que está formada por la mitad superior del círculo unitario en un plano y la gráfica de\(f(x,y)=2\).

Para ver que\(\displaystyle \int_C 2 \,ds=2\pi\) usando la definición de integral de línea, dejamos\(\vecs r(t)\) ser una parametrización de\(C\). Entonces,\(f(\vecs r(t_i))=2\) para cualquier número\(t_i\) en el dominio de\(\vecs r\). Por lo tanto,

\[\begin{align*} \int_C f \,ds &=\lim_{n\to\infty}\sum_{i=1}^{n} f(\vecs r(t_{i}^{*}))\,\Delta s_i \\[4pt] &=\lim_{n\to\infty}\sum_{i=1}^{n}2\,\Delta s_i \\[4pt] &=2\lim_{n\to\infty}\sum_{i=1}^{n}\,\Delta s_i \\[4pt] &=2(\text{length}\space \text{of}\space C) \\[4pt] &=2\pi \,\text{units}^2. \end{align*}\]

Ejercicio\(\PageIndex{1}\)

Encuentra el valor de\(\displaystyle \int_C(x+y)\,ds\), donde\(C\) está la curva parametrizada por\(x=t\),\(y=t\),\(0≤t≤1\).

Pista

Encuentra la forma formada por\(C\) y la gráfica de función\(f(x,y)=x+y\).

Contestar

\(\sqrt{2}\)

Tenga en cuenta que en una integral de línea escalar, la integración se realiza con respecto a la longitud del arco\(s\), lo que puede hacer que una línea escalar integral sea difícil de calcular. Para facilitar los cálculos, podemos traducir\(\displaystyle \int_C f\,ds\) a una integral con una variable de integración que es\(t\).

Que\(\vecs r(t)=⟨x(t),y(t),z(t)⟩\) para\(a≤t≤b\) ser una parametrización de\(C\). Ya que estamos asumiendo que\(C\) es suave,\(\vecs r′(t)=⟨x′(t),y′(t),z′(t)⟩\) es continuo para todos\(t\) adentro\([a,b]\). En particular,\(x′(t)\),\(y′(t)\), y\(z′(t)\) existir para todos\(t\) en\([a,b]\). De acuerdo con la fórmula de longitud de arco, tenemos

\[\text{length}(C_i)=\Delta s_i=\int_{t_{i−1}}^{t_i} ‖\vecs r′(t)‖\,dt. \nonumber \]

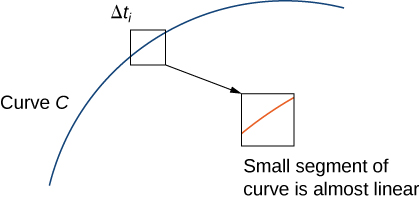
Si el ancho\(\Delta t_i=t_i−t_{i−1}\) es pequeño, entonces la función\(\displaystyle \int_{t_{i−1}}^{t_i} ‖\vecs r′(t)‖\,dt\,≈\,‖\vecs r′(t_i^*)‖\,\Delta t_i\),\(‖\vecs r′(t)‖\) es casi constante a lo largo del\([t_{i−1},t_i]\) intervalo.Por lo tanto,

\[\int_{t_{i−1}}^{t_i} ‖\vecs r′(t)‖\,dt\,≈\,‖\vecs r′(t_{i}^{*})‖\,\Delta t_i, \label{approxLineIntEq1} \]

y tenemos

\[\sum_{i=1}^{n} f(\vecs r(t_i^*))\,\Delta s_i\approx\sum_{i=1}^{n} f(\vecs r(t_{i}^{*})) ‖\vecs r′(t_{i}^{*})‖\,\Delta t_i. \nonumber \]

Ver Figura\(\PageIndex{4}\).

Figura\(\PageIndex{4}\): Si ampliamos la curva lo suficiente haciendo\(\Delta t_i\) muy pequeña, entonces la pieza correspondiente de la curva es aproximadamente lineal.

Tenga en cuenta que

\[\lim_{n\to\infty}\sum_{i=1}^{n} f(\vecs r(t_i^*))‖\vecs r′(t_{i}^{*})‖\,\Delta t_i=\int_a^b f(\vecs r(t))‖\vecs r′(t)‖\,dt. \nonumber \]

En otras palabras, a medida que los anchos de los intervalos se\([t_{i−1},t_i]\) contraen a cero, la suma\(\displaystyle \sum_{i=1}^{n} f(\vecs r(t_i^{*}))‖\vecs r′(t_{i}^{*})‖\,\Delta t_i\) converge a la integral\(\displaystyle \int_{a}^{b}f(\vecs r(t))‖\vecs r′(t)‖\,dt\). Por lo tanto, tenemos el siguiente teorema.

Teorema: Evaluación de una Integral de Línea Escalar

Dejar\(f\) ser una función continua con un dominio que incluye la curva suave\(C\) con parametrización\(\vecs r(t)\),\(a≤t≤b\). Entonces

\[\int_C f \,ds=\int_{a}^{b} f(\vecs r(t))‖\vecs r′(t)‖\,dt.\label{scalerLineInt1} \]

Aunque hemos etiquetado Ecuación\ ref {ApproxLineInteq1} como una ecuación, se considera con mayor precisión una aproximación porque podemos mostrar que el lado izquierdo de la Ecuación\ ref {ApproxLineInteq1} se acerca al lado derecho como\(n\to\infty\). En otras palabras, dejar que los anchos de las piezas se encojan a cero hace que la suma de la derecha se acerque arbitrariamente a la suma de la izquierda. Desde

\[‖\vecs r′(t)‖=\sqrt{{(x′(t))}^2+{(y′(t))}^2+{(z′(t))}^2}, \nonumber \]

obtenemos el siguiente teorema, que utilizamos para calcular integrales de línea escalar.

Teorema: Cálculo Integral de Línea Escalar

Dejar\(f\) ser una función continua con un dominio que incluye la curva suave\(C\) con parametrización\(\vecs r(t)=⟨x(t),y(t),z(t)⟩\),\(a≤t≤b\). Entonces

\[\int_C f(x,y,z) \,ds=\int_{a}^{b} f(\vecs r(t))\sqrt{({x′(t))}^2+{(y′(t))}^2+{(z′(t))}^2} \,dt. \nonumber \]

Del mismo modo,

\[\int_C f(x,y) \,ds=\int_{a}^{b}f(\vecs r(t))\sqrt{{(x′(t))}^2+{(y′(t))}^2} \,dt \nonumber \]

if\(C\) es una curva plana y\(f\) es una función de dos variables.

Obsérvese que una consecuencia de este teorema es la ecuación\(ds=‖\vecs r′(t)‖ \,dt\). En otras palabras, el cambio en la longitud del arco se puede ver como un cambio en el\(t\) dominio, escalado por la magnitud del vector\(\vecs r′(t)\).

Ejemplo\(\PageIndex{2}\): Evaluating a Line Integral

Encuentra el valor de integral\(\displaystyle \int_C(x^2+y^2+z) \,ds\), donde\(C\) forma parte de la hélice parametrizada por\(\vecs r(t)=⟨\cos t,\sin t,t⟩\),\(0≤t≤2\pi\).

Solución

Para calcular una integral de línea escalar, comenzamos convirtiendo la variable de integración de longitud de arco\(s\) a\(t\). Entonces, podemos usar la Ecuación\ ref {eq12a} para calcular la integral con respecto a\(t\). Tenga en cuenta que

\[f(\vecs r(t))={\cos}^2 t+{\sin}^2 t+t=1+t \nonumber \]

y

\[\sqrt{{(x′(t))}^2+{(y′(t))}^2+{(z′(t))}^2} =\sqrt{{(−\sin(t))}^2+{\cos}^2(t)+1} =\sqrt{2}.\nonumber \]

Por lo tanto,

\[\int_C(x^2+y^2+z) \,ds=\int_{0}^{2\pi} (1+t)\sqrt{2} \,dt. \nonumber \]

Observe que la ecuación\ ref {eq12a} tradujo la integral original de la línea difícil en una integral manejable de una sola variable. Desde

\ [\ begin {align*}\ int_ {0} ^ {2\ pi} (1+t)\ sqrt {2}\, dt &= {\ left [\ sqrt {2} t+\ dfrac {\ sqrt {2} t^2} {2}\ derecha]} _ {0} ^ {2\ pi}\\ [4pt]
&=2\ sqrt {2}\ pi+2\ sqrt {2} {\ pi} ^2,\ end {alinear*}\]

tenemos

\[\int_C(x^2+y^2+z) \,ds=2\sqrt{2}\pi+2\sqrt{2}{\pi}^2. \nonumber \]

Ejercicio\(\PageIndex{2}\)

Evaluar\(\displaystyle \int_C(x^2+y^2+z)ds\), donde C es la curva con parametrización\(\vecs r(t)=⟨\sin(3t),\cos(3t)⟩\),\(0≤t≤\dfrac{\pi}{4}\).

Pista

Utilice la versión de dos variables de definición integral de línea escalar (Ecuación\ ref {eq13}).

Contestar

\[\dfrac{1}{3}+\dfrac{\sqrt{2}}{6}+\dfrac{3\pi}{4} \nonumber \]

Ejemplo\(\PageIndex{3}\): Independence of Parameterization

Encuentra el valor de integral\(\displaystyle \int_C(x^2+y^2+z) \,ds\), donde\(C\) forma parte de la hélice parametrizada por\(\vecs r(t)=⟨\cos(2t),\sin(2t),2t⟩\),\(0≤t≤π\). Observe que esta función y curva son las mismas que en el ejemplo anterior; la única diferencia es que la curva ha sido reparameterizada para que el tiempo transcurra el doble de rápido.

Solución

Al igual que con el ejemplo anterior, utilizamos la Ecuación\ ref {eq12a} para calcular la integral con respecto a\(t\). Tenga en cuenta que\(f(\vecs r(t))={\cos}^2(2t)+{\sin}^2(2t)+2t=2t+1\) y

\ [\ begin {align*}\ sqrt {{(x′ (t))} ^2+ {(y′ (t))} ^2+ {(z′ (t))} ^2} &=\ sqrt {(−\ sin t+\ cos t+4)}\\ [4pt] &=22
\ end {align*}\]

así que tenemos

\[\begin{align*} \int_C(x^2+y^2+z)ds &=2\sqrt{2}\int_{0}^{\pi}(1+2t)dt\\[4pt] &=2\sqrt{2}\Big[t+t^2\Big]_0^{\pi} \\[4pt] &=2\sqrt{2}(\pi+{\pi}^2). \end{align*}\]

Observe que esto concuerda con la respuesta del ejemplo anterior. Cambiar la parametrización no cambió el valor de la integral de línea. Las integrales de línea escalar son independientes de la parametrización, siempre que la curva sea atravesada exactamente una vez por la parametrización.

Ejercicio\(\PageIndex{3}\)

Evaluar integral de línea\(\displaystyle \int_C(x^2+yz) \,ds\), donde\(C\) está la línea con parametrización\(\vecs r(t)=⟨2t,5t,−t⟩\),\(0≤t≤10\). Reparameterizar C con parametrización\(s(t)=⟨4t,10t,−2t⟩\)\(0≤t≤5\), recalcular integral\(\displaystyle \int_C(x^2+yz) \,ds\) de línea y notar que el cambio de parametrización no tuvo efecto sobre el valor de la integral.

Pista

Utilice la ecuación\ ref {eq12a}.

Contestar

Ambas integrales de línea son iguales\(−\dfrac{1000\sqrt{30}}{3}\).

Ahora que podemos evaluar integrales de línea, podemos usarlas para calcular la longitud del arco. Si\(f(x,y,z)=1\), entonces

\[\begin{align*} \int_C f(x,y,z) \,ds &=\lim_{n\to\infty} \sum_{i=1}^{n} f(t_{i}^{*}) \,\Delta s_i \\[4pt] &=\lim_{n\to\infty} \sum_{i=1}^{n} \,\Delta s_i \\[4pt] &=\lim_{n\to\infty} \text{length} (C)\\[4pt] &=\text{length} (C). \end{align*}\]

Por lo tanto,\(\displaystyle \int_C 1 \,ds\) es la longitud del arco de\(C\).

Ejemplo\(\PageIndex{4}\): Calculating Arc Length

Un cable tiene una forma que se puede modelar con la parametrización\(\vecs r(t)=⟨\cos t,\sin t,\frac{2}{3} t^{3/2}⟩\),\(0≤t≤4\pi\). Encuentra la longitud del cable.

Solución

La longitud del cable viene dada por\(\displaystyle \int_C 1 \,ds\), donde\(C\) está la curva con parametrización\(\vecs r\). Por lo tanto,

\[\begin{align*} \text{The length of the wire} &=\int_C 1 \,ds \\[4pt] &=\int_{0}^{4\pi} ||\vecs r′(t)||\,dt \\[4pt] &=\int_{0}^{4\pi} \sqrt{(−\sin t)^2+\cos^2 t+t}dt \\[4pt] &=\int_{0}^{4\pi} \sqrt{1+t} dt \\[4pt] &=\left.\dfrac{2{(1+t)}^{\frac{3}{2}}}{3} \right|_{0}^{4\pi} \\[4pt] &=\frac{2}{3}\left((1+4\pi)^{3/2}−1\right). \end{align*}\]

Ejercicio\(\PageIndex{4}\)

Encuentra la longitud de un cable con parametrización\(\vecs r(t)=⟨3t+1,4−2t,5+2t⟩\),\(0≤t≤4\).

Pista

Encuentra la línea integral de uno sobre la curva correspondiente.

Responder

\(4\sqrt{17}\)

Integrales de línea vectorial

El segundo tipo de integrales de línea son integrales de línea vectorial, en las que nos integramos a lo largo de una curva a través de un campo vectorial. Por ejemplo, vamos

\[\vecs F(x,y,z)=P(x,y,z)\,\hat{\mathbf i}+Q(x,y,z)\,\hat{\mathbf j}+R(x,y,z)\,\hat{\mathbf k} \nonumber \]

ser un campo vectorial continuo en\(ℝ^3\) que representa una fuerza sobre una partícula, y dejar\(C\) ser una curva suave\(ℝ^3\) contenida en el dominio de\(\vecs F\). ¿Cómo calcularíamos el trabajo realizado al\(\vecs F\) mover una partícula\(C\)?

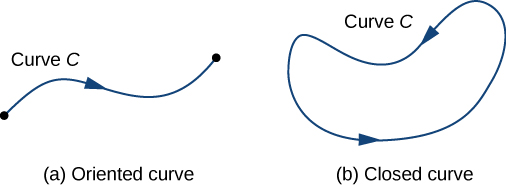
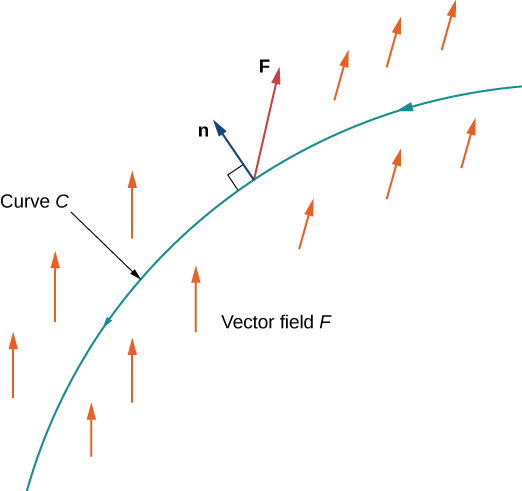
Para responder a esta pregunta, primero tenga en cuenta que una partícula podría viajar en dos direcciones a lo largo de una curva: una dirección hacia adelante y una dirección hacia atrás. El trabajo realizado por el campo vectorial depende de la dirección en la que se mueve la partícula. Por lo tanto, debemos especificar una dirección a lo largo de la curva\(C\); dicha dirección especificada se denomina orientación de una curva. La dirección especificada es la dirección positiva a lo largo\(C\); la dirección opuesta es la dirección negativa a lo largo\(C\). Cuando se le\(C\) ha dado una orientación,\(C\) se denomina curva orientada (Figura\(\PageIndex{5}\)). El trabajo realizado sobre la partícula depende de la dirección a lo largo de la curva en la que se mueve la partícula.

Una curva cerrada es aquella para la que existe una parametrización\(\vecs r(t)\),\(a≤t≤b\), tal que\(\vecs r(a)=\vecs r(b)\), y la curva se recorre exactamente una vez. En otras palabras, la parametrización es uno a uno en el dominio\((a,b)\).

Figura\(\PageIndex{5}\): (a) Una curva orientada entre dos puntos. b) Una curva cerrada orientada.

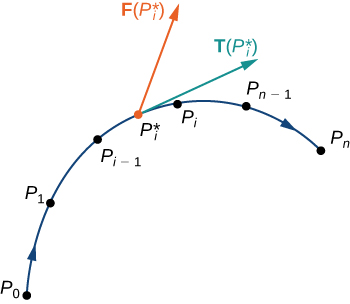
\(\vecs r(t)\)Sea una parametrización de\(C\) para\(a≤t≤b\) tal que la curva sea atravesada exactamente una vez por la partícula y la partícula se mueva en la dirección positiva a lo largo\(C\). Divida el intervalo de parámetros\([a,b]\) en n subintervalos\([t_{i−1},t_i]\)\(0≤i≤n\),, de igual ancho. Denotar los puntos finales de\(r(t_0)\),\(r(t_1)\),...,\(r(t_n)\) por\(P_0\),...,\(P_n\). Los puntos\(C\) se\(P_i\) dividen en n pedazos. Denote la longitud de la pieza de\(P_{i−1}\) a\(P_i\) por\(\Delta s_i\). Para cada uno\(i\), elija un valor\(t_i^*\) en el subintervalo\([t_{i−1},t_i]\). Entonces, el punto final de\(\vecs r(t_i^*)\) es un punto en la pieza de\(C\) entre\(P_{i−1}\) y\(P_i\) (Figura\(\PageIndex{6}\)). Si\(\Delta s_i\) es pequeño, entonces a medida que la partícula se mueve de\(P_{i−1}\) a\(P_i\) lo largo\(C\), se mueve aproximadamente en la dirección de\(\vecs T(P_i)\), el vector tangente unitario en el punto final de\(\vecs r(t_i^*)\). Dejar\(P_i^*\) denotar el punto final de\(\vecs r(t_i^*)\). Entonces, el trabajo realizado por el campo del vector de fuerza al mover la partícula de\(P_{i−1}\) a\(P_i\) es\(\vecs F(P_i^*)·(\Delta s_i \vecs T(P_i^*))\), por lo que el trabajo total realizado a lo largo\(C\) es

\[\sum_{i=1}^n \vecs F(P_i^*)·(\Delta s_i \vecs T(P_i^*))=\sum_{i=1}^n \vecs F(P_i^*)·\vecs T(P_i^*)\,\Delta s_i. \nonumber \]

Figura\(\PageIndex{6}\): La curva\(C\) se divide en n piezas, y se elige un punto dentro de cada pieza. El producto de punto de cualquier vector tangente en la i-ésima pieza con el vector correspondiente\(\vecs{F}\) se aproxima por\(\vecs{F}(P_i^*) \cdot \vecs{T}(P_i^*)\).

Dejar que la longitud del arco de las piezas se\(C\) haga arbitrariamente pequeña tomando un límite como nos\(n\rightarrow \infty\) da el trabajo realizado por el campo para mover la partícula a lo largo\(C\). Por lo tanto, el trabajo realizado\(\vecs{F}\) al mover la partícula en la dirección positiva a lo largo\(C\) se define como

\[W=\int_C \vecs{F} \cdot \vecs{T}\,ds, \nonumber \]

lo que nos da el concepto de una integral de línea vectorial.

DEFINICIÓN: Línea Integral de un Campo Vectorial

La integral de línea vectorial del campo vectorial\(\vecs{F}\) a lo largo de la curva suave orientada\(C\) es

\[\int_C \vecs{F} \cdot \vecs{T}\, ds=\lim_{n\to\infty} \sum_{i=1}^{n} \vecs{F}(P_i^*) \cdot \vecs{T}(P_i^*)\Delta s_i \nonumber \]

si ese límite existe.

Con las integrales de línea escalar, ni la orientación ni la parametrización de la curva importan. Siempre y cuando la curva sea atravesada exactamente una vez por la parametrización, el valor de la integral de línea no cambia. Con las integrales de línea vectorial, la orientación de la curva sí importa. Si pensamos en la línea integral como un trabajo de computación, entonces esto tiene sentido: si subes a una montaña, entonces la fuerza gravitacional de la Tierra te hace un trabajo negativo. Si caminas por la montaña exactamente por el mismo camino, entonces la fuerza gravitacional de la Tierra te hace un trabajo positivo. Es decir, invertir el camino cambia el valor de trabajo de negativo a positivo en este caso. Tenga en cuenta que si\(C\) es una curva orientada, entonces dejamos\(−C\) representar la misma curva pero con orientación opuesta.

Al igual que con las integrales de línea escalar, es más fácil calcular una integral de línea vectorial si la expresamos en términos de la función de parametrización\(\vecs{r}\) y la variable\(t\). Para traducir la integral\(\displaystyle \int_C \vecs{F} \cdot \vecs{T}ds\) en términos de\(t\), tenga en cuenta que el vector tangente unitario\(\vecs{T}\) a lo largo\(C\) viene dado por\(\vecs{T}=\dfrac{\vecs{r}′(t)}{‖\vecs{r}′(t)‖}\) (asumiendo\(‖\vecs{r}′(t)‖≠0\)). Ya que\(ds=‖\vecs r′(t)‖\,dt\), como vimos al discutir integrales de línea escalar, tenemos

\[\vecs F·\vecs T\,ds=\vecs F(\vecs r(t))·\dfrac{\vecs r′(t)}{‖\vecs r′(t)‖}‖\vecs r′(t)‖dt=\vecs F(\vecs r(t))·\vecs r′(t)\,dt. \nonumber \]

Así, tenemos la siguiente fórmula para calcular integrales de línea vectorial:

\[\int_C\vecs F·\vecs T\,ds=\int_a^b \vecs F(\vecs r(t))·\vecs r′(t)\,dt.\label{lineintformula} \]

Debido a la ecuación\ ref {lineintformula}, a menudo usamos la notación\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\) para la integral de línea\(\displaystyle \int_C \vecs F·\vecs T\,ds\).

Si\(\vecs r(t)=⟨x(t),y(t),z(t)⟩\), entonces\(\dfrac{d\vecs{r}}{dt}\) denota vector\(⟨x′(t),y′(t),z′(t)⟩\), y\(d\vecs{r} = \vecs r'(t)\,dt\).

Ejemplo\(\PageIndex{5}\): Evaluating a Vector Line Integral

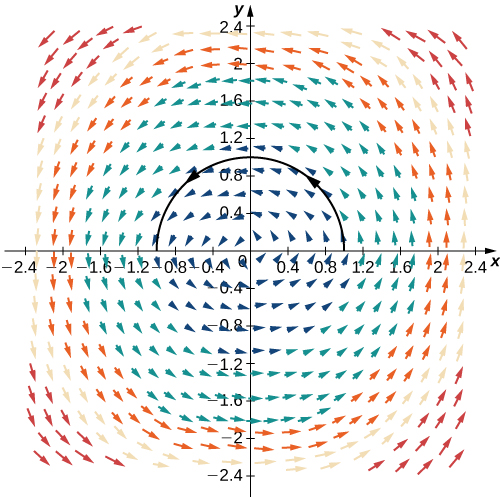
Encuentra el valor de integral\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\), donde\(C\) es el semicírculo parametrizado por\(\vecs{r}(t)=⟨\cos t,\sin t⟩\),\(0≤t≤\pi\) y\(\vecs F=⟨−y,x⟩\).

Solución

Podemos usar la ecuación\ ref {lineintformula} para convertir la variable de integración de\(s\) a\(t\). Entonces tenemos

\[\vecs F(\vecs r(t))=⟨−\sin t,\cos t⟩ \; \text{and} \; \vecs r′(t)=⟨−\sin t,\cos t⟩ . \nonumber \]

Por lo tanto,

\[\begin{align*} \int_C \vecs{F} \cdot d\vecs{r} &=\int_0^{\pi}⟨−\sin t,\cos t⟩·⟨−\sin t,\cos t⟩ \,dt \\[4pt] &=\int_0^{\pi} {\sin}^2 t+{\cos}^2 t \,dt \\[4pt] &=\int_0^{\pi}1 \,dt=\pi.\end{align*}\]

Ver Figura\(\PageIndex{7}\).

Figura\(\PageIndex{7}\): Esta figura muestra la curva\(\vecs r(t)=⟨\cos t,\,\sin t⟩\),\(0≤t≤\pi\) en campo vectorial\(\vecs F=⟨−y,\,x⟩\).

Ejemplo\(\PageIndex{6}\): Reversing Orientation

Encuentra el valor de integral\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\), donde\(C\) es el semicírculo parametrizado por\(\vecs r(t)=⟨\cos (t+π),\sin t⟩\),\(0≤t≤\pi\) y\(\vecs F=⟨−y,x⟩\).

Solución

Observe que este es el mismo problema que Ejemplo\(\PageIndex{5}\), excepto que la orientación de la curva ha sido atravesada. En este ejemplo, la parametrización comienza en\(\vecs r(0)=⟨-1,0⟩\) y termina en\(\vecs r(\pi)=⟨1,0⟩\). Por Ecuación\ ref {lineintformula},

\[\begin{align*} \int_C \vecs{F} \cdot d\vecs{r} &=\int_0^{\pi} ⟨−\sin t,\cos (t+\pi)⟩·⟨−\sin (t+\pi), \cos t⟩dt\\[4pt] &=\int_0^{\pi}⟨−\sin t,−\cos t⟩·⟨\sin t,\cos t⟩dt\\[4pt] &=\int_{0}^{π}(−{\sin}^2 t−{\cos}^2 t)dt \\[4pt] &=\int_{0}^{\pi}−1dt\\[4pt] &=−\pi. \end{align*}\]

Observe que esto es lo negativo de la respuesta en Ejemplo\(\PageIndex{5}\). Tiene sentido que esta respuesta sea negativa porque la orientación de la curva va en contra del “flujo” del campo vectorial.

Dejar\(C\) ser una curva orientada y dejar\(-C\) denotar la misma curva pero con la orientación invertida. Luego, los dos ejemplos anteriores ilustran el siguiente hecho:

\[\int_{-C} \vecs{F} \cdot d\vecs{r}=−\int_C\vecs{F} \cdot d\vecs{r}. \nonumber \]

Es decir, al invertir la orientación de una curva se cambia el signo de una integral de línea.

Ejercicio\(\PageIndex{6}\)

Dejar\(\vecs F=x\,\hat{\mathbf i}+y \,\hat{\mathbf j}\) ser un campo vectorial y dejar\(C\) ser la curva con parametrización\(⟨t,t^2⟩\) para\(0≤t≤2\). ¿Cuál es mayor:\(\displaystyle \int_C\vecs F·\vecs T\,ds\) o\(\displaystyle \int_{−C} \vecs F·\vecs T\,ds\)?

Pista

Imagínese moverse por el camino y calcular el producto punto a\(\vecs F·\vecs T\) medida que avanza.

Responder

\[\int_C \vecs F·\vecs T \,ds \nonumber \]

Otra notación estándar para integral\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\) es\(\displaystyle \int_C P\,dx+Q\,dy+R \,dz\). En esta notación,\(P,\, Q\), y\(R\) son funciones, y pensamos en ellas\(d\vecs{r}\) como vector\(⟨dx,dy,dz⟩\). Para justificar esta convención, recordemos eso\(d\vecs{r}=\vecs T\,ds=\vecs r′(t) \,dt=\left\langle\dfrac{dx}{dt},\dfrac{dy}{dt},\dfrac{dz}{dt}\right\rangle\,dt\). Por lo tanto,

\[\vecs{F} \cdot d\vecs{r}=⟨P,Q,R⟩·⟨dx,dy,dz⟩=P\,dx+Q\,dy+R\,dz. \nonumber \]

Si\(d\vecs{r}=⟨dx,dy,dz⟩\), entonces\(\dfrac{dr}{dt}=\left\langle\dfrac{dx}{dt},\dfrac{dy}{dt},\dfrac{dz}{dt}\right\rangle\), lo que implica eso\(d\vecs{r}=\left\langle\dfrac{dx}{dt},\dfrac{dy}{dt},\dfrac{dz}{dt}\right\rangle\,dt\). Por lo tanto

\[\begin{align} \int_C \vecs{F} \cdot d\vecs{r} &=\int_C P\,dx+Q\,dy+R\,dz \\[4pt] &=\int_a^b\left(P\big(\vecs r(t)\big)\dfrac{dx}{dt}+Q\big(\vecs r(t)\big)\dfrac{dy}{dt}+R\big(\vecs r(t)\big)\dfrac{dz}{dt}\right)\,dt. \label{eq14}\end{align} \]

Ejemplo\(\PageIndex{7}\): Finding the Value of an Integral of the Form \(\displaystyle \int_C P\,dx+Q\,dy+R\,dz\)

Encuentra el valor de integral\(\displaystyle \int_C z\,dx+x\,dy+y\,dz\), donde\(C\) está la curva parametrizada por\(\vecs r(t)=⟨t^2,\sqrt{t},t⟩\),\(1≤t≤4\).

Solución

Al igual que con nuestros ejemplos anteriores, para calcular esta línea integral debemos realizar un cambio de variables para escribir todo en términos de\(t\). En este caso, la Ecuación\ ref {eq14} nos permite realizar este cambio:

\[\begin{align*} \int_C z\,dx+x\,dy+y\,dz &=\int_1^4 \left(t(2t)+t^2\left(\frac{1}{2\sqrt{t}}\right)+\sqrt{t}\right)\,dt \\[4pt] &=\int_1^4\left(2t^2+\frac{t^{3/2}}{2}+\sqrt{t}\right)\,dt \\[4pt] &={\left[\dfrac{2t^3}{3}+\dfrac{t^{5/2}}{5}+\dfrac{2t^{3/2}}{3} \right]}_{t=1}^{t=4} \\[4pt] &=\dfrac{793}{15}.\end{align*}\]

Ejercicio\(\PageIndex{7}\)

Encuentra el valor de\(\displaystyle \int_C 4x\,dx+z\,dy+4y^2\,dz\), donde\(C\) está la curva parametrizada por\(\vecs r(t)=⟨4\cos(2t),2\sin(2t),3⟩\),\(0≤t≤\dfrac{\pi}{4}\).

Pista

Escribe la integral en términos de\(t\) usar la ecuación\ ref {eq14}.

Responder

\(−26\)

Hemos aprendido a integrar curvas de orientación suave. Ahora bien, supongamos que\(C\) es una curva orientada que no es lisa, sino que puede escribirse como la unión de finitamente muchas curvas suaves. En este caso, decimos que\(C\) es una curva lisa por tramos. Para ser precisos, la curva\(C\) es lisa por partes si se\(C\) puede escribir como una unión de n curvas suaves,,...\(C_1\)\(C_2\), de\(C_n\) tal manera que el punto final de\(C_i\) es el punto de partida de\(C_{i+1}\) (Figura\(\PageIndex{8}\)). Cuando las curvas\(C_i\) satisfacen la condición de que el punto final de\(C_i\) es el punto de partida de\(C_{i+1}\), escribimos su unión como\(C_1+C_2+⋯+C_n\).

Figura\(\PageIndex{8}\): La unión de\(C_1\),\(C_2\),\(C_3\) es una curva lisa por tramos.

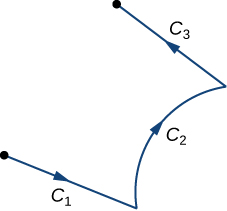
El siguiente teorema resume varias propiedades clave de las integrales de líneas vectoriales.

Teorema: Propiedades de Integrales de Línea Vectorial

Let\(\vecs F\) y\(\vecs G\) ser campos vectoriales continuos con dominios que incluyen la curva suave orientada\(C\). Entonces

1. \(\displaystyle \int_C(\vecs F+\vecs G)·d\vecs{r}=\int_C \vecs{F} \cdot d\vecs{r}+\int_C \vecs G·d\vecs{r}\)
2. \(\displaystyle \int_C k\vecs{F} \cdot d\vecs{r}=k\int_C \vecs{F} \cdot d\vecs{r}\), donde\(k\) es una constante
3. \(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}=\int_{−C}\vecs{F} \cdot d\vecs{r}\)
4. Supongamos en cambio que\(C\) es una curva lisa por tramos en los dominios de\(\vecs F\) y\(\vecs G\), donde\(C=C_1+C_2+⋯+C_n\) y\(C_1,C_2,…,C_n\) son curvas suaves de tal manera que el punto final de\(C_i\) es el punto de partida de\(C_{i+1}\). Entonces

   \[\int_C \vecs F·d\vecs{r}=\int_{C_1} \vecs F·d\vecs{r}+\int_{C_2} \vecs F·d\vecs{r}+⋯+\int_{C_n} \vecs F·d\vecs{r}. \nonumber \]

Observe las similitudes entre estos ítems y las propiedades de integrales de una sola variable. Las propiedades i. y ii. dicen que las integrales de línea son lineales, lo que también es cierto para integrales de una sola variable. Propiedad iii. dice que invertir la orientación de una curva cambia el signo de la integral. Si pensamos en lo integral como computar el trabajo realizado en una partícula que viaja a lo largo\(C\), entonces esto tiene sentido. Si la partícula se mueve hacia atrás en lugar de hacia adelante, entonces el valor del trabajo realizado tiene el signo opuesto. Esto es análogo a la ecuación\(\displaystyle \int_a^b f(x)\,dx=−\int_b^af(x)\,dx\). Por último, si\([a_1,a_2]\)\([a_2,a_3]\),,...,\([a_{n−1},a_n]\) son intervalos, entonces

\[\int_{a_1}^{a_n}f(x) \,dx=\int_{a_1}^{a_2}f(x)\,dx+\int_{a_1}^{a_3}f(x)\,dx+⋯+\int_{a_{n−1}}^{a_n} f(x)\,dx, \nonumber \]

que es análogo a la propiedad iv.

Ejemplo\(\PageIndex{8}\): Using Properties to Compute a Vector Line Integral

Encuentra el valor de integral\(\displaystyle \int_C \vecs F·\vecs T \,ds\), donde\(C\) está el rectángulo (orientado en sentido antihorario) en un plano con vértices\((0,0)\)\((2,0)\),\((2,1)\),, y\((0,1)\), y donde\(\vecs F=⟨x−2y,y−x⟩\) (Figura\(\PageIndex{9}\)).

Figura\(\PageIndex{9}\): Rectángulo y campo vectorial para Ejemplo\(\PageIndex{8}\).

Solución

Tenga en cuenta que la curva\(C\) es la unión de sus cuatro lados, y cada lado es liso. Por lo tanto,\(C\) es liso a trozos. Dejar\(C_1\) representar el lado de\((0,0)\) a\((2,0)\), dejar\(C_2\) representar el lado de\((2,0)\) a\((2,1)\), dejar\(C_3\) representar el lado de\((2,1)\) a\((0,1)\), y dejar\(C_4\) representar el lado de\((0,1)\) a\((0,0)\) (Figura\(\PageIndex{9}\)). Entonces,

\[\int_C \vecs F·\vecs T \,dr=\int_{C_1} \vecs F·\vecs T \,dr+\int_{C_2} \vecs F·\vecs T \,dr+\int_{C_3} \vecs F·\vecs T \,dr+\int_{C_4} \vecs F·\vecs T \,dr. \nonumber \]

Queremos calcular cada una de las cuatro integrales en el lado derecho usando la ecuación\ ref {eq12a}. Antes de hacer esto, necesitamos una parametrización de cada lado del rectángulo. Aquí hay cuatro parametrizaciones (tenga en cuenta que atraviesan en\(C\) sentido antihorario):

\[\begin{align*} C_1&: ⟨t,0⟩,0≤t≤2\\[4pt] C_2&: ⟨2,t⟩, 0≤t≤1 \\[4pt] C_3&: ⟨2−t,1⟩, 0≤t≤2\\[4pt] C_4&: ⟨0,1−t⟩, 0≤t≤1. \end{align*}\]

Por lo tanto,

\[\begin{align*} \int_{C_1} \vecs F·\vecs T \,dr &=\int_0^2 \vecs F(\vecs r(t))·\vecs r′(t) \,dt \\[4pt] &=\int_0^2 ⟨t−2(0),0−t⟩·⟨1,0⟩ \,dt=\int_0^2 t \,dt \\[4pt] &=\Big[\tfrac{t^2}{2}\Big]_0^2=2. \end{align*}\]

Observe que el valor de esta integral es positivo, lo que no debería sorprender. A medida que avanzamos a lo largo\(C_1\) de la curva de izquierda a derecha, nuestro movimiento fluye en la dirección general del campo vectorial mismo. En cualquier punto a lo largo\(C_1\), el vector tangente a la curva y el vector correspondiente en el campo forman un ángulo que es menor a 90°. Por lo tanto, el vector tangente y el vector de fuerza tienen un producto de punto positivo a lo largo\(C_1\), y la integral de línea tendrá un valor positivo.

Los cálculos para las otras tres integrales de línea se realizan de manera similar:

\[\begin{align*} \int_{C_2} \vecs{F} \cdot d\vecs{r} &=\int_{0}^{1}⟨2−2t,t−2⟩·⟨0,1⟩ \,dt \\[4pt] &=\int_{0}^{1} (t−2) \,dt \\[4pt] &=\Big[\tfrac{t^2}{2}−2t\Big]_0^1=−\dfrac{3}{2}, \end{align*}\]

\[\begin{align*} \int_{C_3} \vecs F·\vecs T \,ds &=\int_0^2⟨(2−t)−2,1−(2−t)⟩·⟨−1,0⟩ \,dt \\[4pt] &=\int_0^2t \,dt=2, \end{align*}\]

y

\[\begin{align*} \int_{C_4} \vecs{F} \cdot d\vecs{r} &=\int_0^1⟨−2(1−t),1−t⟩·⟨0,−1⟩ \,dt \\[4pt] &=\int_0^1(t−1) \,dt \\[4pt] &=\Big[\tfrac{t^2}{2}−t\Big]_0^1=−\dfrac{1}{2}. \end{align*}\]

Así, tenemos\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}=2\).

Ejercicio\(\PageIndex{8}\)

Calcular integral de línea\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\), donde\(\vecs F\) es campo vectorial\(⟨y^2,2xy+1⟩\) y\(C\) es un triángulo con vértices\((0,0)\),\((4,0)\), y\((0,5)\), orientado en sentido antihorario.

Pista

Escribe el triángulo como una unión de sus tres lados, luego calcula tres integrales de línea separadas.

Responder

0

Aplicaciones de Integrales de Línea

Las integrales de línea escalar tienen muchas aplicaciones. Se pueden utilizar para calcular la longitud o masa de un cable, el área de superficie de una hoja de una altura determinada o el potencial eléctrico de un cable cargado dada una densidad de carga lineal. Las integrales de líneas vectoriales son extremadamente útiles en física. Se pueden utilizar para calcular el trabajo realizado en una partícula a medida que se mueve a través de un campo de fuerza, o el caudal de un fluido a través de una curva. Aquí, calculamos la masa de un alambre usando una integral de línea escalar y el trabajo realizado por una fuerza usando una integral de línea vectorial.

Supongamos que un trozo de alambre está modelado por la curva C en el espacio. La masa por unidad de longitud (la densidad lineal) del cable es una función continua\(\rho(x,y,z)\). Podemos calcular la masa total del alambre utilizando la integral de línea escalar\(\displaystyle \int_C \rho(x,y,z) \,ds\). La razón es que la masa es densidad multiplicada por longitud, y por lo tanto la densidad de una pequeña pieza del alambre puede aproximarse por\(\rho(x^*,y^*,z^*) \,\Delta s\) por algún punto\((x^*,y^*,z^*)\) de la pieza. Dejar que la longitud de las piezas se contraigan a cero con un límite produce la integral de la línea\(\displaystyle \int_C \rho(x,y,z) \,ds\).

Ejemplo\(\PageIndex{9}\): Calculating the Mass of a Wire

Calcular la masa de un resorte en forma de curva parametrizada por\(⟨t,2\cos t,2\sin t⟩\),\(0≤t≤\dfrac{\pi}{2}\), con una función de densidad dada por\(\rho(x,y,z)=e^x+yz\) kg/m (Figura\(\PageIndex{10}\)).

Figura\(\PageIndex{10}\): El cable del Ejemplo\(\PageIndex{9}\).

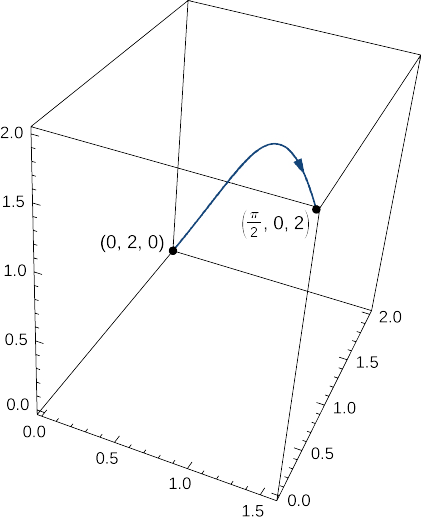
Solución

Para calcular la masa del resorte, debemos encontrar el valor de la línea escalar integral\(\displaystyle \int_C(e^x+yz)\,ds\), donde\(C\) está la hélice dada. Para calcular esta integral, la escribimos en términos de\(t\) usar la ecuación\ ref {eq12a}:

\[\begin{align*} \int_C \left(e^x+yz\right) \,ds &=\int_0^{\tfrac{\pi}{2}} \left((e^t+4\cos t\sin t)\sqrt{1+(−2\cos t)^2+(2\sin t)^2}\right)\,dt\\[4pt] &=\int_0^{\tfrac{\pi}{2}}\left((e^t+4\cos t\sin t)\sqrt{5}\right) \,dt \\[4pt] &=\sqrt{5}\Big[e^t+2\sin^2 t\Big]_{t=0}^{t=\pi/2}\\[4pt] &=\sqrt{5}(e^{\pi/2}+1). \end{align*}\]

Por lo tanto, la masa es de\(\sqrt{5}(e^{\pi/2}+1)\) kg.

Ejercicio\(\PageIndex{9}\)

Calcular la masa de un resorte en forma de hélice parametrizada por\(\vecs r(t)=⟨\cos t,\sin t,t⟩\),\(0≤t≤6\pi\), con una función de densidad dada por\(\rho (x,y,z)=x+y+z\) kg/m.

Pista

Calcular la integral de línea de\(\rho\) sobre la curva con parametrización\(\vecs r\).

Responder

\(18\sqrt{2}{\pi}^2\)kg

Cuando definimos por primera vez las integrales de líneas vectoriales, utilizamos el concepto de trabajo para motivar la definición. Por lo tanto, no es sorprendente que calcular el trabajo realizado por un campo vectorial que representa una fuerza sea un uso estándar de integrales de líneas vectoriales. Recordemos que si un objeto se mueve a lo largo de la curva\(C\) en el campo de fuerza\(\vecs F\), entonces el trabajo requerido para mover el objeto viene dado por\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\).

Ejemplo\(\PageIndex{10}\): ​​​​​​Calculating Work

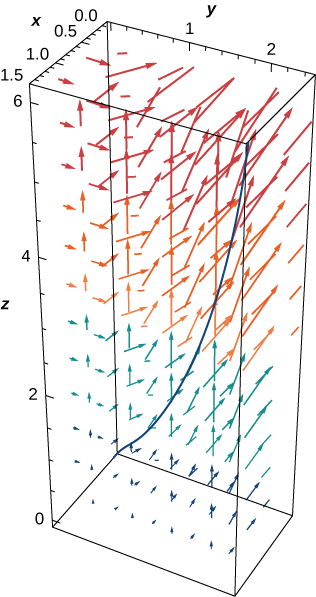
Cuánto trabajo se requiere para mover un objeto en el campo de fuerza vectorial\(\vecs F=⟨yz,xy,xz⟩\) a lo largo de la trayectoria\(\vecs r(t)=⟨t^2,t,t^4⟩,\, 0≤t≤1?\) Ver Figura\(\PageIndex{11}\).

Solución

Vamos a\(C\) denotar el camino dado. Tenemos que encontrar el valor de\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\). Para ello, usamos la ecuación\ ref {lineintformula}:

\[\begin{align*}\int_C \vecs{F} \cdot d\vecs{r} &=\int_0^1(⟨t^5,t^3,t^6⟩·⟨2t,1,4t^3⟩) \,dt \\[4pt] &=\int_0^1(2t^6+t^3+4t^9) \,dt \\[4pt] &={\Big[\dfrac{2t^7}{7}+\dfrac{t^4}{4}+\dfrac{2t^{10}}{5}\Big]}_{t=0}^{t=1}=\dfrac{131}{140}\;\text{units of work}. \end{align*}\]

Figura\(\PageIndex{11}\): La curva y el campo vectorial para Ejemplo\(\PageIndex{10}\).

Flux

Cerramos esta sección discutiendo dos conceptos clave relacionados con las integrales de línea: flujo a través de una curva plana y circulación a lo largo de una curva plana. El flujo se utiliza en aplicaciones para calcular el flujo de fluido a través de una curva, y el concepto de circulación es importante para caracterizar campos de gradiente conservadores en términos de integrales de línea. Ambos conceptos son muy utilizados a lo largo del resto de este capítulo. La idea de flujo es especialmente importante para el teorema de Green, y en dimensiones superiores para el teorema de Stokes y el teorema de divergencia.

Dejar\(C\) ser una curva plana y dejar\(\vecs F\) ser un campo vectorial en el plano. Imagínese\(C\) es una membrana a través de la cual fluye el fluido, pero\(C\) no impide el flujo del fluido. En otras palabras,\(C\) es una membrana idealizada invisible al fluido. Supongamos que\(\vecs F\) representa el campo de velocidad del fluido. ¿Cómo podríamos cuantificar la velocidad a la que se cruza el fluido\(C\)?

Recordemos que la integral de línea\(\vecs F\) a lo largo\(C\) es\(\displaystyle \int_C \vecs F·\vecs T \,ds\) —en otras palabras, la integral de línea es el producto de puntos del campo vectorial con el vector tangencial unitario con respecto a la longitud del arco. Si reemplazamos el vector tangencial unitario con vector normal unitario\(\vecs N(t)\) y en su lugar computamos integral\(\int_C \vecs F·\vecs N \,ds\), determinamos el flujo transversal\(C\). Para ser precisos, la definición de integral\(\displaystyle \int_C \vecs F·\vecs N \,ds\) es la misma que integral\(\displaystyle \int_C \vecs F·\vecs T \,ds\), salvo que la\(\vecs T\) en la suma de Riemann se sustituye por\(\vecs N\). Por lo tanto, el flujo\(C\) transversal se define como

\[\int_C \vecs F·\vecs N \,ds=\lim_{n\to\infty}\sum_{i=1}^{n} \vecs F(P_i^*)·\vecs N(P_i^*)\,\Delta s_i, \nonumber \]

donde\(P_i^*\) y\(\Delta s_i\) se definen como fueron para integral\(\displaystyle \int_C \vecs F·\vecs T \,ds\). Por lo tanto, una integral de flujo es una integral que es perpendicular a una integral de línea vectorial, porque\(\vecs N\) y\(\vecs T\) son vectores perpendiculares.

Si\(\vecs F\) es un campo de velocidad de un fluido y\(C\) es una curva que representa una membrana, entonces el flujo de\(\vecs F\) través\(C\) es la cantidad de fluido que fluye\(C\) por unidad de tiempo, o la velocidad de flujo.

De manera más formal, deje\(C\) ser una curva plana parametrizada por\(\vecs r(t)=⟨x(t),\,y(t)⟩\),\(a≤t≤b\). Dejar\(\vecs n(t)=⟨y′(t),\,−x′(t)⟩\) ser el vector que es normal a\(C\) en el punto final de\(\vecs r(t)\) y apunta a la derecha a medida que atravesamos\(C\) en la dirección positiva (Figura\(\PageIndex{12}\)). Entonces,\(\vecs N(t)=\dfrac{\vecs n(t)}{‖\vecs n(t)‖}\) es el vector normal de la unidad a\(C\) en el punto final de\(\vecs r(t)\) ese apunta a la derecha a medida que atravesamos\(C\).

DEFINICIÓN: Flujo

El flujo de\(\vecs F\) través\(C\) es integral de línea

\[\int_C \vecs F·\dfrac{\vecs n(t)}{‖\vecs n(t)‖} \,ds. \nonumber \]

Figura\(\PageIndex{12}\): El flujo de campo vectorial\(\vecs F\) a través de la curva\(C\) se calcula mediante una integral similar a una integral de línea vectorial.

Ahora damos una fórmula para calcular el flujo a través de una curva. Esta fórmula es análoga a la fórmula utilizada para calcular una integral de línea vectorial (ver Ecuación\ ref {lineintfórmula}).

Teorema: Cálculo del flujo a través de una curva

Dejar\(\vecs F\) ser un campo vectorial y dejar\(C\) ser una curva suave con parametrización\(r(t)=⟨x(t),y(t)⟩\),\(a≤t≤b\) .Let\(\vecs n(t)=⟨y′(t),−x′(t)⟩\). El flujo de\(\vecs F\) través\(C\) es

\[\int_C \vecs F·\vecs N\,ds=\int_a^b\vecs F(\vecs r(t))·\vecs n(t) \,dt. \label{eq84} \]

Prueba

Antes de derivar la fórmula, tenga en cuenta que

\[‖\vecs n(t)‖=‖⟨y′(t),−x′(t)⟩‖=\sqrt{{(y′(t))}^2+{(x′(t))}^2}=‖\vecs r′(t)‖. \nonumber \]

Por lo tanto,

\[\begin{align*}\int_C \vecs F·\vecs N \,ds &=\int_C \vecs F·\dfrac{\vecs n(t)}{‖\vecs n(t)‖} \,ds \\[4pt] &=\int_a^b \vecs F·\dfrac{\vecs n(t)}{‖\vecs n(t)‖}‖\vecs r′(t)‖ \,dt \\[4pt] &=\int_a^b \vecs F(\vecs r(t))·\vecs n(t) \,dt. \end{align*}\]

\(\square\)

Ejemplo\(\PageIndex{11}\): Flux across a Curve

Calcular el flujo de\(\vecs F=⟨2x,2y⟩\) a través de un círculo unitario orientado en sentido antihorario (Figura\(\PageIndex{13}\)).

Figura\(\PageIndex{13}\): Un círculo unitario en campo vectorial\(\vecs F=⟨2x,\,2y⟩\).

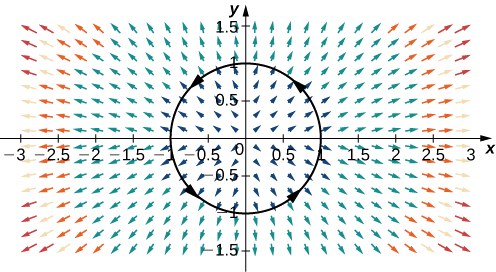
Solución

Para calcular el flujo, primero necesitamos una parametrización del círculo unitario. Podemos utilizar la parametrización estándar\(\vecs r(t)=⟨\cos t,\sin t⟩\),\(0≤t≤2\pi\). El vector normal a un círculo unitario es\(⟨\cos t,\sin t⟩\). Por lo tanto, el flujo es

\[\begin{align*} \int_C \vecs F·\vecs N \,ds &=\int_0^{2\pi}⟨2\cos t,2\sin t⟩·⟨\cos t,\sin t⟩ \,dt\\[4pt] &=\int_0^{2\pi}(2{\cos}^2t+2{\sin}^2t) \,dt \\[4pt] &=2\int_0^{2\pi}({\cos}^2t+{\sin}^2t) \,dt \\[4pt] &=2\int_0^{2\pi} \,dt=4\pi.\end{align*}\]

Ejercicio\(\PageIndex{11}\)

Calcular el flujo de\(\vecs F=⟨x+y,2y⟩\) a través del segmento de línea de\((0,0)\) a\((2,3)\), donde la curva se orienta de izquierda a derecha.

Pista

Usa la ecuación\ ref {eq84}.

Responder

\(3/2\)

Let\(\vecs F(x,y)=⟨P(x,y),Q(x,y)⟩\) Ser un campo vectorial bidimensional. Recordemos que integral a veces\(\displaystyle \int_C \vecs F·\vecs T \,ds\) se escribe como\(\displaystyle \int_C P\,dx+Q\,dy\). Análogamente, el flujo a veces\(\displaystyle \int_C \vecs F·\vecs N \,ds\) se escribe en la notación\(\displaystyle \int_C −Q\,dx+P\,dy\), porque el vector normal unitario\(\vecs N\) es perpendicular a la tangente unitaria\(\vecs T\). Girar el vector\(d\vecs{r}=⟨dx,dy⟩\) 90° resulta en vector\(⟨dy,−dx⟩\). Por lo tanto, la línea integral en Ejemplo se\(\PageIndex{8}\) puede escribir como\(\displaystyle \int_C −2y\,dx+2x\,dy\).

Circulación

Ahora que hemos definido el flujo, podemos dirigir nuestra atención a la circulación. La integral de línea del campo vectorial\(\vecs F\) a lo largo de una curva cerrada orientada se llama circulación de\(\vecs F\) lo largo\(C\). Las integrales de la línea de circulación tienen su propia notación:\(\oint_C \vecs F·\vecs T \,ds\). El círculo en el símbolo integral denota que\(C\) es “circular” en que no tiene puntos finales. Ejemplo\(\PageIndex{5}\) muestra un cálculo de circulación.

Para ver de dónde viene el término circulación y qué mide, vamos a\(\vecs v\) representar el campo de velocidad de un fluido y dejar que\(C\) sea una curva cerrada orientada. En un punto particular\(P\), cuanto más cerca esté la dirección de\(\vecs v(P)\) a la dirección de\(\vecs T(P)\), mayor será el valor del producto de punto\(\vecs v(P)·\vecs T(P)\). El valor máximo de\(\vecs v(P)·\vecs T(P)\) ocurre cuando los dos vectores están apuntando en la misma dirección exacta; el valor mínimo de\(\vecs v(P)·\vecs T(P)\) ocurre cuando los dos vectores están apuntando en direcciones opuestas. Así, el valor de la circulación\(\oint_C \vecs v·\vecs T \,ds\) mide la tendencia del fluido a moverse en la dirección de\(C\).

Ejemplo\(\PageIndex{12}\): Calculating Circulation

Dejar\(\vecs F=⟨−y,\,x⟩\) ser el campo vectorial de Ejemplo\(\PageIndex{3}\) y dejar\(C\) representar el círculo unitario orientado en sentido antihorario. Calcular la circulación de\(\vecs F\) lo largo\(C\).

Solución

Utilizamos la parametrización estándar del círculo unitario:\(\vecs r(t)=⟨\cos t,\sin t⟩\),\(0≤t≤2\pi\). Entonces,\(\vecs F(\vecs r(t))=⟨−\sin t,\cos t⟩\) y\(\vecs r′(t)=⟨−\sin t,\cos t⟩\). Por lo tanto, la circulación de\(\vecs F\) lo largo\(C\) es

\[\begin{align*} \oint_C \vecs F·\vecs T \,ds &=\int_0^{2\pi}⟨−\sin t,\cos t⟩·⟨−\sin t,\cos t⟩ \,dt \\[4pt] &=\int_0^{2\pi} ({\sin}^2 t+{\cos}^2 t) \,dt \\[4pt] &=\int_0^{2\pi} \,dt=2\pi \;\text{units of work}. \end{align*}\]

Observe que la circulación es positiva. La razón de esto es que la orientación de los\(C\) “flujos” con la dirección de\(\vecs F\). En cualquier punto a lo largo del círculo, el vector tangente y el vector\(\vecs F\) forman un ángulo de menos de 90°, y por lo tanto el producto de punto correspondiente es positivo.

En Ejemplo\(\PageIndex{12}\), ¿y si hubiéramos orientado el círculo unitario en sentido horario? Denotamos el círculo unitario orientado hacia la derecha por\(−C\). Entonces

\[\oint_{−C} \vecs F·\vecs T \,ds=−\oint_C \vecs F·\vecs T \,ds=−2\pi \;\text{units of work}. \nonumber \]

Observe que la circulación es negativa en este caso. La razón de esto es que la orientación de la curva fluye en contra de la dirección de\(\vecs F\).

Ejercicio\(\PageIndex{12}\)

Calcular la circulación de\(\vecs F(x,y)=⟨−\dfrac{y}{x^2+y^2},\,\dfrac{x}{x^2+y^2}⟩\) a lo largo de un círculo unitario orientado en sentido antihorario.

Pista

Usa la ecuación\ ref {eq84}.

Responder

\(2\pi\)unidades de trabajo

Ejemplo\(\PageIndex{13}\): Calculating Work

Calcular el trabajo realizado sobre una partícula que atraviesa círculo\(C\) de radio 2 centrada en el origen, orientada en sentido antihorario, por campo\(\vecs F(x,y)=⟨−2,\,y⟩\). Supongamos que la partícula inicia su movimiento en\((1,\,0)\).

Solución

El trabajo realizado por\(\vecs F\) sobre la partícula es la circulación de\(\vecs F\) lo largo\(C\):\(\oint_C \vecs F·\vecs T \,ds\). Utilizamos la parametrización\(\vecs r(t)=⟨2\cos t,\,2\sin t⟩\),\(0≤t≤2\pi\) para\(C\). Entonces,\(\vecs r′(t)=⟨−2\sin t,\,2\cos t⟩\) y\(\vecs F(\vecs r(t))=⟨−2,\,2\sin t⟩\). Por lo tanto, la circulación de\(\vecs F\) lo largo\(C\) es

\[\begin{align*} \oint_C \vecs F·\vecs T \,ds &=\int_0^{2\pi} ⟨−2,2\sin t⟩·⟨−2\sin t,2\cos t⟩ \,dt\\[4pt] &=\int_0^{2\pi} (4\sin t+4\sin t\cos t) \,dt\\[4pt] &={\Big[−4\cos t+4{\sin}^2 t\Big]}_0^{2\pi}\\[4pt] &=\left(−4\cos(2\pi)+2{\sin}^2(2\pi)\right)−\left(−4\cos(0)+4{\sin}^2(0)\right)\\[4pt] &=−4+4=0\;\text{units of work}.\end{align*}\]

El campo de fuerza hace trabajo cero sobre la partícula.

Observe que la circulación de\(\vecs F\) lo largo\(C\) es cero. Además, observe que ya que\(\vecs F\) es el gradiente de\(f(x,y)=−2x+\dfrac{y^2}{2}\),\(\vecs F\) es conservador. Demostramos en una sección posterior que bajo ciertas condiciones amplias, la circulación de un campo vectorial conservador a lo largo de una curva cerrada es cero.

Ejercicio\(\PageIndex{14}\)

Calcular el trabajo realizado por campo\(\vecs F(x,y)=⟨2x,\,3y⟩\) sobre una partícula que atraviesa el círculo unitario. Supongamos que la partícula comienza su movimiento en\((−1,\,0)\).

Pista

Usa la ecuación\ ref {eq84}.

Responder

\(0\)unidades de trabajo

Conceptos clave

• Las integrales de línea generalizan la noción de integral de una sola variable a dimensiones superiores. El dominio de integración en una integral de variable única es un segmento lineal a lo largo del\(x\) eje -eje, pero el dominio de integración en una integral de línea es una curva en un plano o en el espacio.
• Si\(C\) es una curva, entonces la longitud de\(C\) es\(\displaystyle \int_C \,ds\).
• Hay dos tipos de integral de línea: integrales de línea escalar e integrales de línea vectorial. Las integrales de línea escalar se pueden usar para calcular la masa de un cable; las integrales de línea vectorial se pueden usar para calcular el trabajo realizado en una partícula que viaja a través de un campo.
• Las integrales de línea escalar se pueden calcular usando la ecuación\ ref {eq12a}; las integrales de línea vectorial se pueden calcular usando la ecuación\ ref {lineintformula}.
• Dos conceptos clave expresados en términos de integrales de línea son flujo y circulación. El flujo mide la velocidad a la que un campo cruza una línea dada; la circulación mide la tendencia de un campo a moverse en la misma dirección que una curva cerrada dada.

Ecuaciones Clave

• Cálculo de una integral de línea escalar
  \(\displaystyle \int_C f(x,y,z) \,ds=\int_a^bf(\vecs r(t))\sqrt{{(x′(t))}^2+{(y′(t))}^2+{(z′(t))}^2} \,dt\)
• Calcular una integral de línea vectorial
  \(\displaystyle \int_C \vecs F·d\vecs{r}=\int_C \vecs F·\vecs T \,ds=\int_a^b\vecs F(\vecs r(t))·\vecs r′(t)\,dt\)
  o
  \(\displaystyle \int_C P\,dx+Q\,dy+R\,dz=\int_a^b \left(P\big(\vecs r(t)\big)\dfrac{dx}{dt}+Q\big(\vecs r(t)\big)\dfrac{dy}{dt}+R\big(\vecs r(t)\big)\dfrac{dz}{dt}\right) \,dt\)
• Cálculo de flujo
  \(\displaystyle \int_C \vecs F·\dfrac{\vecs n(t)}{‖\vecs n(t)‖}\,ds=\int_a^b \vecs F(\vecs r(t))·\vecs n(t) \,dt\)

Glosario

circulación

la tendencia de un fluido a moverse en la dirección de la curva\(C\). Si\(C\) es una curva cerrada, entonces la circulación de\(\vecs F\) lo largo\(C\) es línea integral\(∫_C \vecs F·\vecs T \,ds\), que también denotamos\(∮_C\vecs F·\vecs T \,ds\).

curva cerrada

una curva para la que existe una parametrización\(\vecs r(t), a≤t≤b\), tal que\(\vecs r(a)=\vecs r(b)\), y la curva se recorre exactamente una vez

flujo

la velocidad de un fluido que fluye a través de una curva en un campo vectorial; el flujo de campo vectorial\(\vecs F\) a través de la curva plana\(C\) es integral de línea\(∫_C \vecs F·\frac{\vecs n(t)}{‖\vecs n(t)‖} \,ds\)

línea integral

la integral de una función a lo largo de una curva en un plano o en el espacio

orientación de una curva

la orientación de una curva\(C\) es una dirección especificada de\(C\)

curva lisa por tramos

una curva orientada que no es suave, pero que se puede escribir como la unión de finitamente muchas curvas suaves

integral de línea escalar

la integral de línea escalar de una función a\(f\) lo largo de una curva\(C\) con respecto a la longitud del arco es la integral\(\displaystyle \int_C f\,ds\), es la integral de una función escalar\(f\) a lo largo de una curva en un plano o en el espacio; dicha integral se define en términos de una suma de Riemann, como es una integral de una sola variable

integral de línea vectorial

la integral de línea vectorial del campo vectorial\(\vecs F\) a lo largo de la curva\(C\) es la integral del producto puntual de\(\vecs F\) con el vector tangente unitario\(\vecs T\) de\(C\) con respecto a la longitud del arco,\(∫_C \vecs F·\vecs T\, ds\); dicha integral se define en términos de una suma de Riemann, similar a una integral de variable única