16.1: Campos vectoriales
- Page ID
- 116763
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Reconocer un campo vectorial en un plano o en el espacio.
- Esboce un campo vectorial a partir de una ecuación dada.
- Identificar un campo conservador y su función potencial asociada.
Los campos vectoriales son una herramienta importante para describir muchos conceptos físicos, como la gravitación y el electromagnetismo, que afectan el comportamiento de los objetos sobre una gran región de un plano o del espacio. También son útiles para hacer frente a comportamientos a gran escala como tormentas atmosféricas o corrientes oceánicas de profundidad. En esta sección, examinamos las definiciones básicas y gráficas de los campos vectoriales para que podamos estudiarlos con más detalle en el resto de este capítulo.
Ejemplos de campos vectoriales
¿Cómo podemos modelar la fuerza gravitacional ejercida por múltiples objetos astronómicos? ¿Cómo podemos modelar la velocidad de las partículas de agua en la superficie de un río? La figura\(\PageIndex{1}\) da representaciones visuales de tales fenómenos.
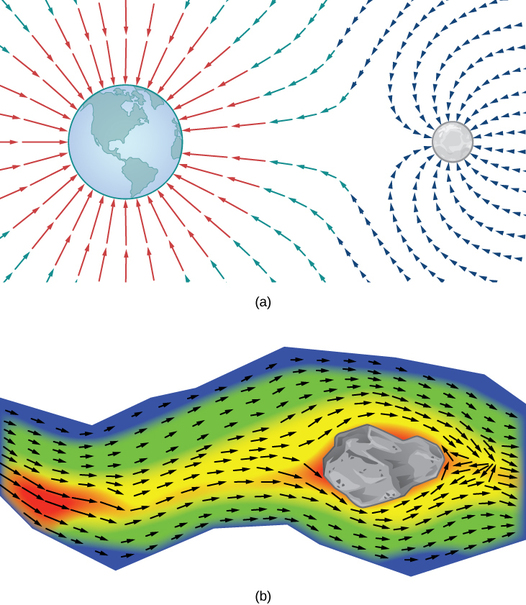
La figura\(\PageIndex{1a}\) muestra un campo gravitacional ejercido por dos objetos astronómicos, como una estrella y un planeta o un planeta y una luna. En cualquier punto de la figura, el vector asociado a un punto da la fuerza gravitacional neta ejercida por los dos objetos sobre un objeto de masa unitaria. Los vectores de mayor magnitud en la figura son los vectores más cercanos al objeto más grande. El objeto más grande tiene mayor masa, por lo que ejerce una fuerza gravitacional de mayor magnitud que el objeto más pequeño.
La figura\(\PageIndex{1b}\) muestra la velocidad de un río en puntos de su superficie. El vector asociado a un punto dado en la superficie del río da la velocidad del agua en ese punto. Dado que los vectores a la izquierda de la figura son pequeños en magnitud, el agua fluye lentamente sobre esa parte de la superficie. A medida que el agua se mueve de izquierda a derecha, se encuentra con algunos rápidos alrededor de una roca. La velocidad del agua aumenta, y se produce un remolino en parte de los rápidos.
Cada figura ilustra un ejemplo de un campo vectorial. Intuitivamente, un campo vectorial es un mapa de vectores. En esta sección, estudiamos campos vectoriales en\(ℝ^2\) y\(ℝ^3\).
- Un campo vectorial\(\vecs{F}\) en\(ℝ^2\) es una asignación de un vector bidimensional\(\vecs{F}(x,y)\) a cada punto\((x,y)\) de un subconjunto\(D\) de\(ℝ^2\). El subconjunto\(D\) es el dominio del campo vectorial.
- Un campo vectorial\(\vecs{F}\) en\(ℝ^3\) es una asignación de un vector tridimensional\(\vecs{F}(x,y,z)\) a cada punto\((x,y,z)\) de un subconjunto\(D\) de\(ℝ^3\). El subconjunto\(D\) es el dominio del campo vectorial.
Campos vectoriales en\(ℝ^2\)
Un campo vectorial en se\(ℝ^2\) puede representar en cualquiera de dos formas equivalentes. La primera forma es usar un vector con componentes que son funciones de dos variables:
\[\vecs{F}(x,y)=⟨P(x,y),Q(x,y)⟩ \nonumber \]
La segunda forma es usar los vectores unitarios estándar:
\[\vecs{F}(x,y)=P(x,y) \,\hat{\mathbf i}+Q(x,y) \,\hat{\mathbf j}. \nonumber \]
Se dice que un campo vectorial es continuo si sus funciones componentes son continuas.
Let\(\vecs{F} (x,y)=(2y^2+x−4)\,\hat{\mathbf i}+\cos(x)\,\hat{\mathbf j}\) Ser un campo vectorial en\(ℝ^2\). Tenga en cuenta que este es un ejemplo de un campo vectorial continuo ya que ambas funciones componentes son continuas. ¿Qué vector está asociado con el punto\((0,−1)\)?
Solución
Sustituir los valores de puntos por\(x\) y\(y\):
\[\begin{align*} \vecs{F} (0,-1) &=(2{(−1)}^2+0−4) \,\hat{\mathbf i}+\cos(0) \,\hat{\mathbf j} \\[4pt] &=−2 \,\hat{\mathbf i} + \hat{\mathbf j}. \end{align*}\]
Let\(\vecs{G}(x,y)=x^2y\,\hat{\mathbf i}−(x+y)\,\hat{\mathbf j}\) Ser un campo vectorial en\(ℝ^2\). ¿Qué vector está asociado con el punto\((−2,3)\)?
- Pista
-
Sustituya los valores de punto en la función de vector.
- Contestar
-
\(\vecs{G}(−2,3)=12\hat{\mathbf i}−\hat{\mathbf j}\)
Dibujar un campo vectorial
Ahora podemos representar un campo vectorial en términos de sus componentes de funciones o vectores unitarios, pero representarlo visualmente dibujándolo es más complejo porque el dominio de un campo vectorial está en\(ℝ^2\), como lo es el rango. Por lo tanto, la “gráfica” de un campo vectorial en\(ℝ^2\) vidas en el espacio de cuatro dimensiones. Como no podemos representar visualmente el espacio de cuatro dimensiones, dibujamos campos vectoriales\(ℝ^2\) en un plano mismo. Para ello, dibuja el vector asociado a un punto dado en el punto de un plano. Por ejemplo, supongamos que el vector asociado al punto\((4,−1)\) es\(⟨3,1⟩\). Entonces, dibujaríamos vector\(⟨3,1⟩\) en punto\((4,−1)\).
Deberíamos trazar suficientes vectores para ver la forma general, pero no tantos como para que el boceto se convierta en un desastre desordenado. Si tuviéramos que trazar el vector de imagen en cada punto de la región, llenaría la región completamente y es inútil. En su lugar, podemos elegir puntos en las intersecciones de líneas de cuadrícula y trazar una muestra de varios vectores de cada cuadrante de un sistema de coordenadas rectangulares en\(ℝ^2\).
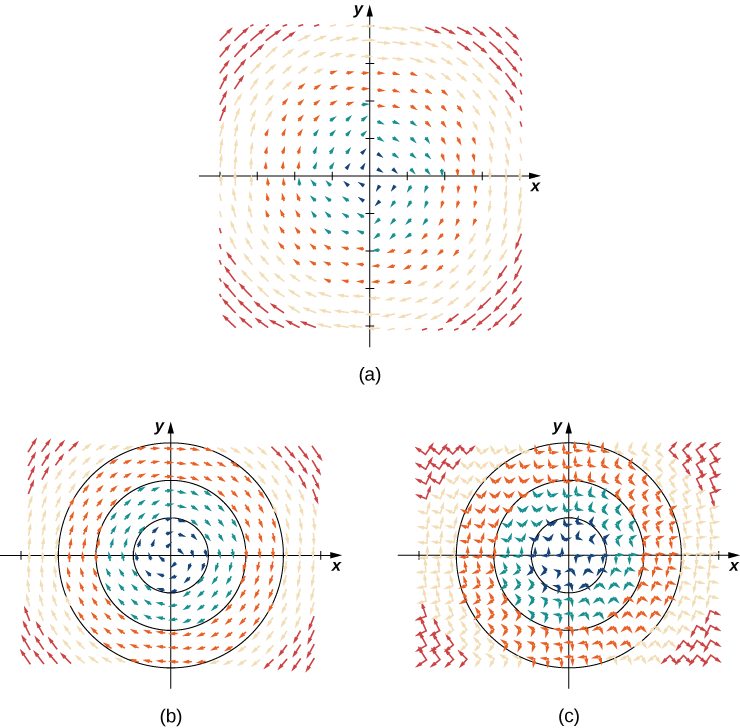
Existen dos tipos de campos vectoriales en\(ℝ^2\) los que se centra este capítulo: los campos radiales y los campos rotacionales. Los campos radiales modelan ciertos campos gravitacionales y campos de fuentes de energía, y los campos rotacionales modelan el movimiento de un fluido en un vórtice. En un campo radial, todos los vectores apuntan directamente hacia o directamente lejos del origen. Además, la magnitud de cualquier vector depende únicamente de su distancia desde el origen. En un campo radial, el vector ubicado en el punto\((x,y)\) es perpendicular al círculo centrado en el origen que contiene el punto\((x,y)\), y todos los demás vectores de este círculo tienen la misma magnitud.
Dibuje el campo vectorial\(\vecs{F} (x,y)=\dfrac{x}{2}\hat{\mathbf i}+\dfrac{y}{2}\hat{\mathbf j}\).
Solución
Para bosquejar este campo vectorial, elija una muestra de puntos de cada cuadrante y calmente el vector correspondiente. La siguiente tabla da una muestra representativa de puntos en un plano y los vectores correspondientes.
| \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) |
|---|---|---|---|---|---|
| \ ((x, y)\)” style="vertical-align:middle; ">\((1,0)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨\dfrac{1}{2},0⟩\) | \ ((x, y)\)” style="vertical-align:middle; ">\((2,0)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨1,0⟩\) | \ ((x, y)\)” style="vertical-align:middle; ">\((1,1)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨\dfrac{1}{2},\dfrac{1}{2}⟩\) |
| \ ((x, y)\)” style="vertical-align:middle; ">\((0,1)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨0,\dfrac{1}{2}⟩\) | \ ((x, y)\)” style="vertical-align:middle; ">\((0,2)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨0,1⟩\) | \ ((x, y)\)” style="vertical-align:middle; ">\((−1,1)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨−\dfrac{1}{2},\dfrac{1}{2}⟩\) |
| \ ((x, y)\)” style="vertical-align:middle; ">\((−1,0)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨−\dfrac{1}{2},0⟩\) | \ ((x, y)\)” style="vertical-align:middle; ">\((−2,0)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨−1,0⟩\) | \ ((x, y)\)” style="vertical-align:middle; ">\((−1,−1)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨−\dfrac{1}{2},−\dfrac{1}{2}⟩\) |
| \ ((x, y)\)” style="vertical-align:middle; ">\((0,−1)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨0,−\dfrac{1}{2}⟩\) | \ ((x, y)\)” style="vertical-align:middle; ">\((0,−2)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨0,−1⟩\) | \ ((x, y)\)” style="vertical-align:middle; ">\((1,−1)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨\dfrac{1}{2},−\dfrac{1}{2}⟩\) |
La figura\(\PageIndex{2a}\) muestra el campo vectorial. Para ver que cada vector es perpendicular al círculo correspondiente, la Figura\(\PageIndex{2b}\) muestra círculos superpuestos en el campo vectorial.
Dibuja el campo radial\(\vecs{F} (x,y)=−\dfrac{x}{3}\hat{\mathbf i}−\dfrac{y}{3}\hat{\mathbf j}\).
- Pista
-
Esboza suficientes vectores para tener una idea de la forma.
- Contestar
-

A diferencia de los campos radiales, en un campo rotacional, el vector en el punto\((x,y)\) es tangente (no perpendicular) a un círculo con radio\(r=\sqrt{x^2+y^2}\). En un campo rotacional estándar, todos los vectores apuntan ya sea en sentido horario o en sentido contrario a las agujas del reloj, y la magnitud de un vector depende únicamente de su distancia desde el origen. Ambos ejemplos siguientes son campos rotacionales en el sentido de las agujas del reloj, y vemos por sus representaciones visuales que los vectores parecen rotar alrededor del origen.
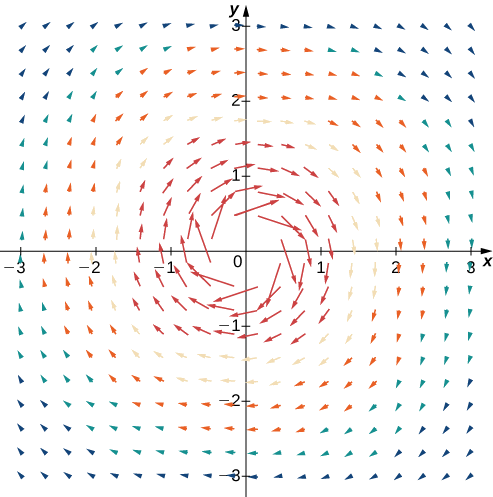
Dibuje el campo vectorial\(\vecs{F} (x,y)=⟨y,\,−x⟩\).
Solución
Crear una tabla (ver la que sigue) utilizando una muestra representativa de puntos en un plano y sus vectores correspondientes. La figura\(\PageIndex{3}\) muestra el campo vectorial resultante.
| \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) |
|---|---|---|---|---|---|
| \ ((x, y)\)” style="vertical-align:middle; ">\((1,0)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨0,−1⟩\) | \ ((x, y)\)” style="vertical-align:middle; ">\((2,0)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨0,−2⟩\) | \ ((x, y)\)” style="vertical-align:middle; ">\((1,1)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨1,−1⟩\) |
| \ ((x, y)\)” style="vertical-align:middle; ">\((0,1)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨1,0⟩\) | \ ((x, y)\)” style="vertical-align:middle; ">\((0,2)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨2,0⟩\) | \ ((x, y)\)” style="vertical-align:middle; ">\((−1,1)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨1,1⟩\) |
| \ ((x, y)\)” style="vertical-align:middle; ">\((−1,0)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨0,1⟩\) | \ ((x, y)\)” style="vertical-align:middle; ">\((−2,0)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨0,2⟩\) | \ ((x, y)\)” style="vertical-align:middle; ">\((−1,−1)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨−1,1⟩\) |
| \ ((x, y)\)” style="vertical-align:middle; ">\((0,−1)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨−1,0⟩\) | \ ((x, y)\)” style="vertical-align:middle; ">\((0,−2)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨−2,0⟩\) | \ ((x, y)\)” style="vertical-align:middle; ">\((1,−1)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨−1,−1⟩\) |
Análisis
Tenga en cuenta que el vector\(\vecs{F}(a,b)=⟨b,−a⟩\) apunta en sentido horario y es perpendicular al vector radial\(⟨a,b⟩\). (Podemos verificar esta afirmación calculando el producto punto de los dos vectores:\(⟨a,b⟩·⟨−b,a⟩=−ab+ab=0\).) Además, el vector\(⟨b,−a⟩\) tiene longitud\(r=\sqrt{a^2+b^2}\). Así, tenemos una descripción completa de este campo vectorial rotacional: el vector asociado con punto\((a,b)\) es el vector con longitud r tangente al círculo con radio r, y apunta en sentido horario.
Bocetos como el de la Figura\(\PageIndex{3}\) se utilizan a menudo para analizar los principales sistemas de tormentas, incluidos huracanes y ciclones. En el hemisferio norte, las tormentas rotan en sentido contrario a las agujas del reloj; en el hemisferio sur, las tormentas rotan (Este es un efecto causado por la rotación de la Tierra alrededor de su eje y se llama Efecto Coriolis).

Campo vectorial de boceto\(\vecs{F}(x,y)=\dfrac{y}{x^2+y^2}\hat{\mathbf i}, -\dfrac{x}{x^2+y^2}\hat{\mathbf j}\).
Solución
Para visualizar este campo vectorial, primero tenga en cuenta que el producto punto\(\vecs{F}(a,b)·(a \,\hat{\mathbf i}+b \,\hat{\mathbf j})\) es cero para cualquier punto\((a,b)\). Por lo tanto, cada vector es tangente al círculo en el que se encuentra. También, como\((a,b)\rightarrow(0,0)\), la magnitud de\(\vecs{F}(a,b)\) va al infinito. Para ver esto, tenga en cuenta que
\(||\vecs{F}(a,b)||=\sqrt{\dfrac{a^2+b^2}{ {(a^2+b^2)}^2 }} =\sqrt{\dfrac{1}{a^2+b^2}}\).
Desde\(\dfrac{1}{a^2+b^2}\rightarrow \infty\) como\((a,b)\rightarrow (0,0)\), entonces\(||\vecs F(a,b)||\rightarrow \infty\) como\((a,b)\rightarrow (0,0)\). Este campo vectorial se parece al campo vectorial en Ejemplo\(\PageIndex{3}\), pero en este caso las magnitudes de los vectores cercanos al origen son grandes. En la tabla se\(\PageIndex{3}\) muestra una muestra de puntos y los vectores correspondientes, y en la Figura se\(\PageIndex{5}\) muestra el campo vectorial. Obsérvese que este campo vectorial modela el movimiento de remolino del río en la Figura\(\PageIndex{5}\) (b). El dominio de este campo vectorial es todo\(ℝ^2\) excepto el punto\((0,0)\).
| \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) |
|---|---|---|---|---|---|
| \ ((x, y)\)” style="vertical-align:middle; ">\((1,0)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨0,−1⟩\) | \ ((x, y)\)” style="vertical-align:middle; ">\((2,0)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨0,−\dfrac{1}{2}⟩\) | \ ((x, y)\)” style="vertical-align:middle; ">\((1,1)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨\dfrac{1}{2},−\dfrac{1}{2}⟩\) |
| \ ((x, y)\)” style="vertical-align:middle; ">\((0,1)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨1,0⟩\) | \ ((x, y)\)” style="vertical-align:middle; ">\((0,2)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨\dfrac{1}{2},0⟩\) | \ ((x, y)\)” style="vertical-align:middle; ">\((−1,1)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨\dfrac{1}{2},\dfrac{1}{2}⟩\) |
| \ ((x, y)\)” style="vertical-align:middle; ">\((−1,0)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨0,1⟩\) | \ ((x, y)\)” style="vertical-align:middle; ">\((−2,0)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨0,\dfrac{1}{2}⟩\) | \ ((x, y)\)” style="vertical-align:middle; ">\((−1,−1)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨−\dfrac{1}{2},\dfrac{1}{2}⟩\) |
| \ ((x, y)\)” style="vertical-align:middle; ">\((0,−1)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨−1,0⟩\) | \ ((x, y)\)” style="vertical-align:middle; ">\((0,−2)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨−\dfrac{1}{2},0⟩\) | \ ((x, y)\)” style="vertical-align:middle; ">\((1,−1)\) | \ (\ vecs {F} (x, y)\)” style="vertical-align:middle; ">\(⟨−\dfrac{1}{2},−\dfrac{1}{2}⟩\) |
Campo vectorial de boceto\(\vecs{F}(x,y)=⟨−2y,\,2x⟩\). ¿El campo vectorial es radial, rotacional o ninguno?
- Pista
-
Sustituye suficientes puntos\(\vecs{F}\) para tener una idea de la forma.
- Contestar
-
Rotacional

Supongamos que\(\vecs{v} (x,y)=−\dfrac{2y}{x^2+y^2}\hat{\mathbf i}+\dfrac{2x}{x^2+y^2}\hat{\mathbf j}\) es el campo de velocidad de un fluido. ¿Qué tan rápido se mueve el fluido en un punto\((1,−1)\)? (Supongamos que las unidades de velocidad son metros por segundo.)
Solución
Para encontrar la velocidad del fluido en el punto\((1,−1)\), sustituya el punto en\(\vecs{v} \):
\(\vecs{v}(1,−1)=\dfrac{−2(−1)}{1+1}\hat{\mathbf i}+\dfrac{2(1)}{1+1}\hat{\mathbf j}=\hat{\mathbf i}+\hat{\mathbf j}\).
La velocidad del fluido a\((1,−1)\) es la magnitud de este vector. Por lo tanto, la velocidad es\(||\hat{\mathbf i}+\hat{\mathbf j}||=\sqrt{2}\) m/seg.
El campo vectorial\(\vecs{v} (x,y)=⟨4|x|,\,1⟩\) modela la velocidad del agua en la superficie de un río. ¿Cuál es la velocidad del agua en el punto\((2,3)\)? Use metros por segundo como las unidades.
- Pista
-
Recuerde, la velocidad es la magnitud de la velocidad.
- Contestar
-
\(\sqrt{65}\)m/seg
Hemos examinado campos vectoriales que contienen vectores de varias magnitudes, pero así como tenemos vectores unitarios, también podemos tener un campo vectorial unitario. Un campo vectorial\(\vecs{F}\) es un campo de vector unitario si la magnitud de cada vector en el campo es 1. En un campo de vector unitario, la única información relevante es la dirección de cada vector.
Mostrar que el campo vectorial\(\vecs{F} (x,y)=\left\langle\dfrac{y}{\sqrt{x^2+y^2}},−\dfrac{x}{\sqrt{x^2+y^2}}\right\rangle\) es un campo de vector de unidad.
Solución
Para mostrar que\(\vecs{F}\) es un campo unitario, debemos mostrar que la magnitud de cada vector es\(1\). Tenga en cuenta que
\[\begin{align*} \sqrt{ \left(\dfrac{y}{\sqrt{x^2+y^2}}\right)^2+\left(−\dfrac{x}{\sqrt{x^2+y^2}}\right)^2} &=\sqrt{ \dfrac{y^2}{x^2+y^2}+\dfrac{x^2}{x^2+y^2}} \\[4pt] &=\sqrt{\dfrac{x^2+y^2}{x^2+y^2}} \\[4pt] &=1 \end{align*}\]
Por lo tanto,\(\vecs{F} \) es un campo de vector unitario.
¿El campo vector es\(\vecs{F} (x,y)=⟨−y,\,x⟩\) un campo de vector unitario?
- Pista
-
Calcular la magnitud de\(\vecs{F} \) en un punto arbitrario\((x,y)\).
- Contestar
-
No.
¿Por qué son importantes los campos vectores unitarios? Supongamos que estamos estudiando el flujo de un fluido, y nos preocupamos únicamente por la dirección en la que fluye el fluido en un punto dado. En este caso, la velocidad del fluido (que es la magnitud del vector de velocidad correspondiente) es irrelevante, porque lo único que nos importa es la dirección de cada vector. Por lo tanto, el campo vector unitario asociado a la velocidad es el campo que estudiaríamos.
Si\(\vecs{F} =⟨P,Q,R⟩\) es un campo vectorial, entonces el campo de vector de unidad correspondiente es\(\big\langle\tfrac{P}{||\vecs F||},\tfrac{Q}{||\vecs F||},\tfrac{R}{||\vecs F||}\big\rangle\). Observe que si\(\vecs{F}(x,y)=⟨y,\,−x⟩\) es el campo vectorial de Ejemplo\(\PageIndex{6}\), entonces la magnitud de\(\vecs{F} \) es\(\sqrt{x^2+y^2}\), y por lo tanto el campo vectorial unitario correspondiente es el campo\(\vecs{G} \) del ejemplo anterior.
Si\(\vecs{F} \) es un campo vectorial, entonces el proceso de dividir\(\vecs{F} \) por su magnitud para formar un campo vectorial unitario\(\vecs{F}/||\vecs{F}||\) se llama normalizar el campo\(\vecs{F} \).
Campos vectoriales en\(ℝ^3\)
Hemos visto varios ejemplos de campos vectoriales en\(ℝ^2\); ahora volvamos nuestra atención a los campos vectoriales en\(ℝ^3\). Estos campos vectoriales se pueden utilizar para modelar campos gravitacionales o electromagnéticos, y también se pueden utilizar para modelar el flujo de fluido o flujo de calor en tres dimensiones. Un campo vectorial bidimensional solo puede modelar el movimiento del agua en una porción bidimensional de un río (como la superficie del río). Dado que un río fluye a través de tres dimensiones espaciales, para modelar el flujo de toda la profundidad del río, necesitamos un campo vectorial en tres dimensiones.
La dimensión extra de un campo tridimensional puede hacer que los campos vectoriales sean\(ℝ^3\) más difíciles de visualizar, pero la idea es la misma. Para visualizar un campo vectorial en\(ℝ^3\), trazar suficientes vectores para mostrar la forma general. Podemos usar un método similar para visualizar un campo vectorial\(ℝ^2\) eligiendo puntos en cada octante.
Al igual que con los campos vectoriales en\(ℝ^2\), podemos representar campos vectoriales\(ℝ^3\) con funciones de componentes. Simplemente necesitamos una función de componente adicional para la dimensión adicional. Escribimos ya sea
\[\vecs{F}(x,y,z)=⟨P(x,y,z),Q(x,y,z),R(x,y,z)⟩ \nonumber \]
o
\[\vecs{F}(x,y,z)=P(x,y,z)\hat{\mathbf i}+Q(x,y,z)\hat{\mathbf j}+R(x,y,z)\hat{\mathbf k}. \nonumber \]
Describir el campo vectorial\(\vecs{F}(x,y,z)=⟨1,\,1,\,z⟩\).
Solución
Para este campo vectorial, los\(y\) componentes\(x\) - y -son constantes, por lo que cada punto en\(ℝ^3\) tiene un vector asociado con\(x\) - y\(y\) -componentes iguales a uno. Para visualizar\(\vecs{F}\), primero consideramos cómo es el campo en el\(xy\) plano -plano. En el\(xy\) -avión,\(z=0\). De ahí que cada punto de la forma\((a,b,0)\) tenga un vector\(⟨1,1,0⟩\) asociado a él. Para los puntos que no están en el\(xy\) plano, sino ligeramente por encima de él, el vector asociado tiene un\(z\) componente pequeño pero positivo, y por lo tanto el vector asociado apunta ligeramente hacia arriba. Para los puntos que están muy por encima del\(xy\) -plano, el\(z\) -componente es grande, por lo que el vector es casi vertical. La figura\(\PageIndex{6}\) muestra este campo vectorial.
Figura\(\PageIndex{6}\): Una representación visual del campo vectorial\(\vecs{F}(x,y,z)=⟨1,1,z⟩\).
Campo vectorial de boceto\(\vecs{G}(x,y,z)=⟨2,\,\dfrac{z}{2},\,1⟩\).
- Pista
-
Sustituye suficientes puntos en el campo vectorial para tener una idea de la forma general.
- Contestar
En el siguiente ejemplo, exploramos uno de los casos clásicos de un campo vectorial tridimensional: un campo gravitacional.
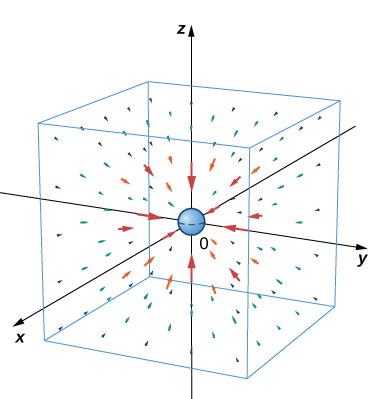
La ley de la gravitación de Newton establece que\(\vecs{F}=−G\dfrac{m_1m_2}{r^2}\hat{\mathbf r}\), donde G es la constante gravitacional universal. Describe el campo gravitacional ejercido por un objeto (objeto 1) de masa\(m_1\) ubicado en el origen sobre otro objeto (objeto 2) de masa\(m_2\) ubicado en el punto\((x,y,z)\). Campo\(\vecs{F}\) denota la fuerza gravitacional que el objeto 1 ejerce sobre el objeto 2,\(r\) es la distancia entre los dos objetos, e\(\hat{\mathbf r}\) indica el vector unitario del primer objeto al segundo. El signo menos muestra que la fuerza gravitacional atrae hacia el origen; es decir, la fuerza del objeto 1 es atractiva. Dibuje el campo vectorial asociado a esta ecuación.
Solución
Dado que el objeto 1 se encuentra en el origen, la distancia entre los objetos viene dada por\(r=\sqrt{x^2+y^2+z^2}\). El vector unitario del objeto 1 al objeto 2 es\(\hat{\mathbf r}=\dfrac{⟨x,y,z⟩}{||⟨x,y,z⟩||}\), y por lo tanto\(\hat{\mathbf r}=\big\langle\dfrac{x}{r},\dfrac{y}{r},\dfrac{z}{r}\big\rangle\). Por lo tanto, el campo vectorial gravitacional\(\vecs{F}\) ejercido por el objeto 1 sobre el objeto 2 es
\[ \vecs{F}=−Gm_1m_2\big\langle\dfrac{x}{r^3},\dfrac{y}{r^3},\dfrac{z}{r^3}\big\rangle. \nonumber \]
Este es un ejemplo de un campo vectorial radial en\(ℝ^3\).
La figura\(\PageIndex{7}\) muestra cómo se ve este campo gravitacional para una gran masa en el origen. Tenga en cuenta que las magnitudes de los vectores aumentan a medida que los vectores se acercan al origen.
La masa del asteroide 1 es de 750,000 kg y la masa del asteroide 2 es de 130,000 kg. Supongamos que el asteroide 1 se encuentra en el origen, y el asteroide 2 se localiza en\((15,−5,10)\), medido en unidades de 10 a los octavos kilómetros de potencia. Dado que la constante gravitacional universal es\(G=6.67384×10^{−11}m^3{kg}^{−1}s^{−2}\), encuentra el vector de fuerza gravitacional que el asteroide 1 ejerce sobre el asteroide 2.
- Pista
-
Siga Ejemplo\(\PageIndex{8}\) y primero compute la distancia entre los asteroides.
- Contestar
-
\(1.49063×{10}^{−18}\),\(4.96876×{10}^{−19}\),\(9.93752×{10}^{−19}\) N
Campos de degradado (Campos conservadores)
En esta sección, estudiamos un tipo especial de campo vectorial llamado campo degradado o campo conservador. Estos campos vectoriales son extremadamente importantes en la física porque pueden ser utilizados para modelar sistemas físicos en los que se conserva la energía. Los campos gravitacionales y eléctricos asociados con una carga estática son ejemplos de campos de gradiente.
Recordemos que si\(f\) es una función (escalar) de\(x\) y\(y\), entonces el gradiente de\(f\) es
\[ \text{grad}\, f =\vecs \nabla f(x,y) =f_x(x,y) \hat{\mathbf i} +f_y(x,y) \hat{\mathbf j}. \nonumber \]
Podemos ver a partir de la forma en la que se escribe el gradiente que\(\vecs \nabla f\) es un campo vectorial en\(ℝ^2\). Del mismo modo, si\(f\) es una función de\(x\)\(y\), y\(z\), entonces el gradiente de\(f\) es
\[ \text{grad}\, f =\vecs \nabla f(x,y,z) = f_x(x,y,z) \hat{\mathbf i}+f_y(x,y,z) \hat{\mathbf j}+f_z(x,y,z)\hat{\mathbf k}. \nonumber \]
El gradiente de una función de tres variables es un campo vectorial en\(ℝ^3\). Un campo de gradiente es un campo vectorial que se puede escribir como el gradiente de una función, y tenemos la siguiente definición.
Un campo vectorial\(\vecs{F}\) en\(ℝ^2\) o en\(ℝ^3\) es un campo de gradiente si existe una función escalar\(f\) tal que\(\vecs \nabla f=\vecs{F}\).
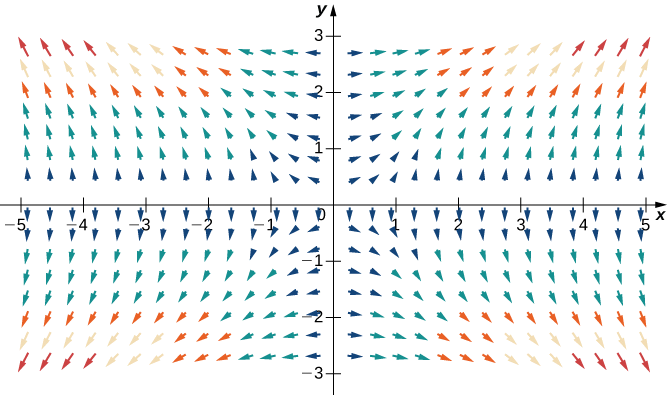
Utilice la tecnología para trazar el campo vectorial de gradiente de\(f(x,y)=x^2y^2\).
Solución
El gradiente de\(f\) es\(\vecs \nabla f(x,y)=⟨2xy^2,\,2x^2y⟩\). Para bosquejar el campo vectorial, utilice un sistema de álgebra computacional como Mathematica. La figura\(\PageIndex{8}\) muestra\(\vecs \nabla f\).
Utilice la tecnología para trazar el campo vectorial de gradiente de\(f(x,y)=\sin x\cos y\).
- Pista
-
Encuentra el gradiente de\(f\).
- Contestar
-
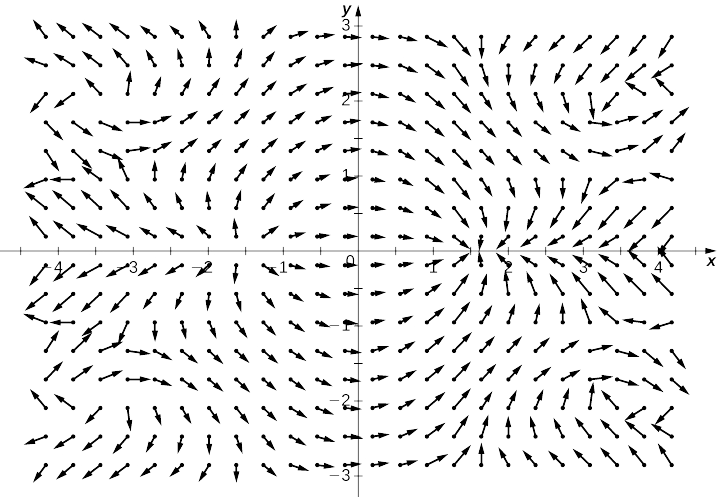
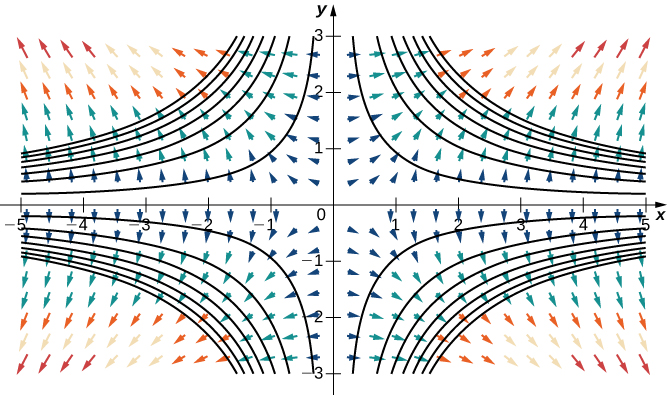
Considera la función\(f(x,y)=x^2y^2\) de Ejemplo\(\PageIndex{9}\). La figura\(\PageIndex{9}\) muestra las curvas de nivel de esta función superpuestas en el campo vectorial de gradiente de la función. Los vectores de gradiente son perpendiculares a las curvas de nivel, y las magnitudes de los vectores se hacen más grandes a medida que las curvas de nivel se acercan, porque las curvas de nivel estrechamente agrupadas indican que la gráfica es empinada, y la magnitud del vector de gradiente es el valor más grande de la derivada direccional. Por lo tanto, puede ver la pendiente local de una gráfica investigando el campo de gradiente de la función correspondiente.
Como aprendimos anteriormente, un campo vectorial\(\vecs{F}\) es un campo vectorial conservador, o un campo de gradiente si existe una función escalar\(f\) tal que\(\vecs \nabla f=\vecs{F}\). En esta situación,\(f\) se llama una función potencial para\(\vecs{F}\). Los campos vectoriales conservadores surgen en muchas aplicaciones, particularmente en física. La razón por la que tales campos son llamados conservadores es que modelan fuerzas de sistemas físicos en los que se conserva la energía. Estudiamos los campos vectoriales conservadores con más detalle más adelante en este capítulo.
Podrías notar que, en algunas aplicaciones, una función potencial\(f\) para\(\vecs{F}\) se define en cambio como una función tal que\(−\vecs \nabla f=\vecs{F}\). Este es el caso de ciertos contextos en física, por ejemplo.
Es\(f(x,y,z)=x^2yz−\sin(xy)\) una función potencial para el campo vectorial
\(\vecs{F}(x,y,z)=⟨2xyz−y\cos(xy),x^2z−x\cos(xy),x^2y⟩\)?
Solución
Tenemos que confirmar si\(\vecs \nabla f=\vecs{F}\). Tenemos
\[ \begin{align*} f_x(x,y) =2xyz−y\cos(xy) \\[4pt] f_y(x,y) =x^2z−x\cos(xy) \\[4pt] f_z(x,y) =x^2y \end{align*}. \nonumber \]
Por lo tanto,\(\vecs \nabla f=\vecs{F}\) y\(f\) es una función potencial para\(\vecs{F}\).
¿Es\(f(x,y,z)=x^2\cos(yz)+y^2z^2\) una función potencial para\(\vecs{F}(x,y,z)=⟨2x\cos(yz),−x^2z \sin(yz)+2yz^2,y^2⟩\)?
- Pista
-
Compute el gradiente de\(f\).
- Contestar
-
No
La velocidad de un fluido es modelada por campo\(\vecs v(x,y)=⟨xy,\tfrac{x^2}{2}−y⟩\). Verificar que\(f(x,y)=\dfrac{x^2y}{2}−\dfrac{y^2}{2}\) sea una función potencial para\(\vecs{v}\).
Solución
Para demostrar que\(f\) es una función potencial, debemos demostrarlo\(\vecs \nabla f=\vecs v\). Tenga en cuenta que\(f_x(x,y)=xy\) y\(f_y(x,y)=\dfrac{x^2}{2}−y\). Por lo tanto,\(\vecs \nabla f(x,y)=⟨xy,\tfrac{x^2}{2}−y⟩\) y\(f\) es una función potencial para\(\vecs{v}\) (Figura\(\PageIndex{10}\)).

Verifique que\(f(x,y)=x^3y^2+x\) sea una función potencial para el campo de velocidad\(\vecs{v}(x,y)=⟨3x^2y^2+1,2x^3y⟩\).
- Pista
-
Calcular el gradiente.
- Contestar
-
\(\vecs \nabla f(x,y)=\vecs{v}(x,y)\)
Si\(\vecs{F}\) es un campo vector conservador, entonces hay al menos una función potencial\(f\) tal que\(\vecs \nabla f=\vecs{F}\). Pero, ¿podría haber más de una función potencial? Si es así, ¿existe alguna relación entre dos funciones potenciales para el mismo campo vectorial? Antes de responder a estas preguntas, recordemos algunos hechos del cálculo de una sola variable para guiar nuestra intuición. Recordemos que si\(k(x)\) es una función integrable, entonces\(k\) tiene infinitamente muchos antiderivados. Además, si\(\vecs{F}\) y\(\vecs{G}\) son ambos antiderivados de\(k\), entonces\(\vecs{F}\) y\(\vecs{G}\) difieren solo por una constante. Es decir, hay algún número\(C\) tal que\(\vecs{F}(x)=\vecs{G}(x)+C\).
Ahora vamos a\(\vecs{F}\) ser un campo vector conservador y dejar\(f\) y\(g\) ser funciones potenciales para\(\vecs{F}\). Dado que el gradiente es como un derivado,\(\vecs{F}\) ser conservador significa que\(\vecs{F}\) es “integrable” con “antiderivados”\(f\) y\(g\). Por lo tanto, si la analogía con el cálculo de una sola variable es válida, esperamos que haya alguna constante\(C\) tal que\(f(x)=g(x)+C\). El siguiente teorema dice que este es efectivamente el caso.
Para afirmar con precisión el siguiente teorema, necesitamos asumir que el dominio del campo vectorial está conectado y abierto. Estar conectado significa si\(P_1\) y\(P_2\) son dos puntos cualesquiera en el dominio, entonces puedes caminar de\(P_1\) a\(P_2\) lo largo de un camino que permanece completamente dentro del dominio.
Dejar\(\vecs{F}\) ser un campo vectorial conservador en un dominio abierto y conectado y dejar\(f\) y\(g\) ser funciones tales que\(\vecs \nabla f=\vecs{F}\) y\(\vecs \nabla g=\vecs{F}\). Entonces, hay una constante\(C\) tal que\(f=g+C\).
Desde\(f\) y\(g\) son ambas funciones potenciales para\(\vecs{F}\), entonces\(\vecs \nabla (f−g)=\vecs \nabla f−\vecs \nabla g=\vecs{F}−\vecs{F}=\vecs 0\). Vamos\(h=f−g\), entonces tenemos\(\vecs \nabla h=\vecs 0\) .Nos gustaría mostrar que\(h\) es una función constante.
Asumir\(h\) es una función de\(x\) y\(y\) (la lógica de esta prueba se extiende a cualquier número de variables independientes). Ya que\(\vecs \nabla h=\vecs 0\), tenemos\(h_x(x,y)=0\) y\(h_y(x,y)=0\). La expresión\(h_x(x,y)=0\) implica que\(h\) es una función constante con respecto a\(x\) —es decir,\(h(x,y)=k_1(y)\) para alguna función\(k_1\). De igual manera,\(h_y(x,y)=0\) implica\(h(x,y)=k_2(x)\) para alguna función\(k_2\). Por lo tanto, la función\(h\) depende sólo de\(y\) y también depende sólo de\(x\). Así,\(h(x,y)=C\) para alguna constante\(C\) en el dominio conectado de\(\vecs{F}\). Tenga en cuenta que realmente necesitamos conectividad en este punto; si el dominio de\(\vecs{F}\) vino en dos piezas separadas, entonces\(k\) podría ser una constante\(C_1\) en una pieza pero podría ser una constante diferente\(C_2\) en la otra pieza. Ya que\(f−g=h=C\), tenemos eso\(f=g+C\), como se desee.
\(\square\)
Los campos vectoriales conservadores también tienen una propiedad especial llamada propiedad cross-partial. Esta propiedad ayuda a probar si un campo vectorial dado es conservador.
Let\(\vecs{F}\) Ser un campo vectorial en dos o tres dimensiones de tal manera que las funciones componentes de\(\vecs{F}\) tienen derivadas continuas mixto-parciales de segundo orden en el dominio de\(\vecs{F}\).
Si\(\vecs{F}(x,y)=⟨P(x,y),Q(x,y)⟩\) es un campo vectorial conservador en\(ℝ^2\), entonces
\[\dfrac{\partial P}{\partial y}=\dfrac{\partial Q}{\partial x}. \nonumber \]
Si\(\vecs{F}(x,y,z)=⟨P(x,y,z),Q(x,y,z),R(x,y,z)⟩\) es un campo vectorial conservador en\({\mathbb{R}}^3\), entonces
\[ \begin{align*} \dfrac{\partial P}{\partial y} =\dfrac{\partial Q}{\partial x} \\[4pt] \dfrac{\partial Q}{\partial z} =\dfrac{\partial R}{\partial y} \\[4pt] \dfrac{\partial R}{\partial x} =\dfrac{\partial P}{\partial z}. \end{align*}\]
Ya que\(\vecs{F}\) es conservadora, hay una función\(f(x,y)\) tal que\(\vecs \nabla f=\vecs{F}\). Por lo tanto, por la definición del gradiente,\(f_x=P\) y\(f_y=Q\). Por el teorema de Clairaut\(f_{xy}=f_{yx}\),, Pero,\(f_{xy}=P_y\) y\(f_{yx}=Q_{x}\), y así\(P_y=Q_x\).
\(\square\)
El teorema de Clairaut da una prueba rápida de la propiedad parcial cruzada de los campos vectoriales conservadores en\(ℝ^3\), tal como lo hizo para los campos vectoriales en\(ℝ^2\).
La propiedad parcial cruzada de los campos vectoriales conservadores muestra que la mayoría de los campos vectoriales no son conservadores. La propiedad parcial cruzada es difícil de satisfacer en general, por lo que la mayoría de los campos vectoriales no tendrán parciales cruzados iguales.
Mostrar que el campo vectorial rotacional no\(\vecs{F}(x,y)=⟨y,\,−x⟩\) es conservador.
Solución
Dejar\(P(x,y)=y\) y\(Q(x,y)=−x\). Si\(\vecs{F}\) es conservador, entonces los interparciales\(P_y\) serían iguales, es decir,\(Q_x\) iguales.Por lo tanto, para demostrar que no \(\vecs{F}\)es conservador, verifíquelo\(P_y≠Q_x\). Desde\(P_y=1\) y\(Q_x=−1\), el campo vectorial no es conservador.
Mostrar que el campo vectorial no\(\vecs F(x,y)=xy\,\hat{\mathbf i}−x^2y\,\hat{\mathbf j}\) es conservador.
- Pista
-
Verifica los partidos cruzados.
- Contestar
-
\(P_y(x,y)=x\)y\(Q_x(x,y)=−2xy\). Ya que\(P_y(x,y) ≠ Q_x(x,y)\), no\(\vecs F\) es conservador.
¿El campo vectorial es\(\vecs{F}(x,y,z)=⟨7,−2,x^3⟩\) conservador?
Solución
Vamos\(P(x,y,z)=7\),\(Q(x,y,z)=−2\), y\(R(x,y,z)=x^3\). Si\(\vecs{F}\) es conservadora, entonces las tres ecuaciones parciales cruzadas quedarán satisfechas, es decir, si\(\vecs{F}\) es conservadora, entonces\(P_y\)\(Q_z\) sería igual\(Q_x\)\(R_y\), igual y\(R_x\) sería igual\(P_z\). Tenga en cuenta que
\[P_y=Q_x=R_y=Q_z=0 \nonumber \]
por lo que se mantienen las dos primeras igualdades necesarias. Sin embargo,\(R_x(x,y,z)=x^3\) y\(P_z(x,y,z)=0\) así\(R_x≠P_z\). Por lo tanto, no\(\vecs{F}\) es conservador.
¿El campo vectorial es\(\vecs{G}(x,y,z)=⟨y,\,x,\,xyz⟩\) conservador?
- Insinuación
-
Verifica los partidos cruzados.
- Contestar
-
No
Concluimos esta sección con una palabra de advertencia: La propiedad transversal parcial de los campos vectoriales conservadores dice que si\(\vecs{F}\) es conservadora, entonces\(\vecs{F}\) tiene la propiedad transversal parcial. El teorema no dice que, si\(\vecs{F}\) tiene la propiedad transversal parcial, entonces\(\vecs{F}\) es conservador (lo contrario de una implicación no es lógicamente equivalente a la implicación original). En otras palabras, La propiedad transversal parcial de los campos vectoriales conservadores solo puede ayudar a determinar que un campo no es conservador; no permite concluir que un campo vectorial es conservador.
Por ejemplo, considere el campo vectorial\(\vecs{F}(x,y)=⟨x^2y,\dfrac{x^3}{3}⟩\). Este campo tiene la propiedad transversal parcial, por lo que es natural intentar usar La propiedad transversal parcial de los campos vectoriales conservadores para concluir que este campo vectorial es conservador. Sin embargo, esta es una mala aplicación del teorema. Más adelante aprendemos a concluir que\(\vecs F\) es conservador.
Conceptos clave
- Un campo vectorial asigna un vector\(\vecs{F}(x,y)\) a cada punto\((x,y)\) en un subconjunto\(D\) de\(ℝ^2\) o\(ℝ^3\). \(\vecs{F}(x,y,z)\)a cada punto\((x,y,z)\) en un subconjunto\(D\) de\(ℝ^3\).
- Los campos vectoriales pueden describir la distribución de cantidades vectoriales tales como fuerzas o velocidades sobre una región del plano o del espacio. Son de uso común en áreas como física, ingeniería, meteorología, oceanografía.
- Podemos esbozar un campo vectorial examinando su ecuación definitoria para determinar magnitudes relativas en varias ubicaciones y luego dibujar suficientes vectores para determinar un patrón.
- Un campo vectorial\(\vecs{F}\) se llama conservador si existe una función escalar\(f\) tal que\(\vecs \nabla f=\vecs{F}\).
Ecuaciones Clave
- Campo vectorial en\(ℝ^2\)
\(\vecs{F}(x,y)=⟨P(x,y),\,Q(x,y)⟩\)
o
\(\vecs{F}(x,y)=P(x,y) \,\hat{\mathbf i}+Q(x,y) \,\hat{\mathbf j}\) - Campo vectorial en\(ℝ^3\)
\(\vecs{F}(x,y,z)=⟨P(x,y,z),\,Q(x,y,z),\,R(x,y,z)⟩\)
o
\(\vecs{F}(x,y,z)=P(x,y,z) \,\hat{\mathbf i} +Q(x,y,z) \,\hat{\mathbf j}+R(x,y,z) \,\hat{\mathbf k}\)
Glosario
- campo conservador
- un campo vectorial para el que existe una función escalar\(f\) tal que\(\vecs ∇f=\vecs{F}\)
- campo degradado
- un campo vectorial\(\vecs{F}\) para el que existe una función escalar\(f\) tal que\(\vecs ∇f=\vecs{F}\); en otras palabras, un campo vectorial que es el gradiente de una función; dichos campos vectoriales también se denominan conservadores
- función potencial
- una función escalar\(f\) tal que\(\vecs ∇f=\vecs{F}\)
- campo radial
- un campo vectorial en el que todos los vectores apuntan directamente hacia o directamente lejos del origen; la magnitud de cualquier vector depende solo de su distancia desde el origen
- campo rotacional
- un campo vectorial en el que el vector en el punto\((x,y)\) es tangente a un círculo con radio\(r=\sqrt{x^2+y^2}\); en un campo rotacional, todos los vectores fluyen ya sea en sentido horario o antihorario, y la magnitud de un vector depende solo de su distancia desde el origen
- campo de vector de unidad
- un campo vectorial en el que la magnitud de cada vector es 1
- campo de vector
- medido en\(ℝ^2\), una asignación de un vector\(\vecs{F}(x,y)\) a cada punto\((x,y)\) de un subconjunto\(D\) de\(ℝ^2\); en\(ℝ^3\), una asignación de un vector\(\vecs{F}(x,y,z)\) a cada punto\((x,y,z)\) de un subconjunto\(D\) de\(ℝ^3\)


