17.1: Ecuaciones lineales de segundo orden
- Page ID
- 116327
- Reconocer ecuaciones diferenciales lineales homogéneas y no homogéneas.
- Determinar la ecuación característica de una ecuación lineal homogénea.
- Utilice las raíces de la ecuación característica para encontrar la solución a una ecuación lineal homogénea.
- Resolver problemas de valor inicial y valor límite que involucran ecuaciones diferenciales lineales.
Cuando se trabaja con ecuaciones diferenciales, generalmente el objetivo es encontrar una solución. En otras palabras, queremos encontrar una función (o funciones) que satisfaga la ecuación diferencial. La técnica que utilizamos para encontrar estas soluciones varía, dependiendo de la forma de la ecuación diferencial con la que estemos trabajando. Las ecuaciones diferenciales de segundo orden tienen varias características importantes que pueden ayudarnos a determinar qué método de solución usar. En esta sección, examinamos algunas de estas características y la terminología asociada.
Ecuaciones lineales homogéneas
Considerar la ecuación diferencial de segundo orden
\[xy''+2x^2y'+5x^3y=0.\nonumber \]
Observe que\(y\) y sus derivados aparecen en una forma relativamente simple. Se multiplican por funciones de\(x\), pero no se elevan a ningún poder ellos mismos, ni se multiplican entre sí. Como se discutió anteriormente, se dice que las ecuaciones de primer orden con características similares son lineales. Lo mismo ocurre con las ecuaciones de segundo orden. Obsérvese también que todos los términos en esta ecuación diferencial involucran a cualquiera\(y\) o a una de sus derivadas. No hay términos que involucren únicamente funciones de\(x\). Ecuaciones como esta, en las que cada término contiene\(y\) o una de sus derivadas, se denominan homogéneas.
No todas las ecuaciones diferenciales son homogéneas. Considerar la ecuación diferencial
\[xy''+2x^2y'+5x^3y=x^2.\nonumber \]
El\(x^2\) término del lado derecho del signo igual no contiene\(y\) ni ninguno de sus derivados. Por lo tanto, esta ecuación diferencial no es homogénea.
Una ecuación diferencial de segundo orden es lineal si se puede escribir en la forma
\[a_{2}(x)y''+a){1}(x)y'+a_{0}(x)y=r(x), \label{17.1} \]
donde\(a_{2}(x), a_{1}(x), a_{0}(x),\) y\(r(x)\) son funciones de valor real y no\(a_{2}(x)\) es idénticamente cero. Si\(r(x) \equiv 0\) —en otras palabras, si\(r(x)=0\) por cada valor de\(x\) —se dice que la ecuación es una ecuación lineal homogénea. Si\(r(x) \neq 0\) por algún valor de\(x,\) la ecuación se dice que es una ecuación lineal no homogénea.
En las ecuaciones diferenciales lineales,\(y\) y sus derivadas solo pueden elevarse a la primera potencia y no pueden multiplicarse entre sí. Términos que involucran\(y^2\) o\(\sqrt{y'}\) hacen que la ecuación no sea lineal. Las funciones de\(y\) y sus derivadas, tales como\(\sin y\) o\(e^{y'}\), están igualmente prohibidas en las ecuaciones diferenciales lineales.
Tenga en cuenta que las ecuaciones no siempre pueden darse en forma estándar (la forma que se muestra en la definición). Puede ser útil reescribirlos en esa forma para decidir si son lineales, o si una ecuación lineal es homogénea.
Clasificar cada una de las siguientes ecuaciones como lineales o no lineales. Si la ecuación es lineal, determine además si es homogénea o no homogénea.
- \(y''+3x^4y'+x^2y^2=x^3\)
- \((\sin x)y''+(\cos x)y'+3y=0\)
- \(4t^2x''+3txx'+4x=0\)
- \(5y''+y=4x^5 \)
- \(( \cos x)y''- \sin y'+( \sin x)y- \cos x=0\)
- \(8ty''-6t^2y'+4ty-3t^2=0 \)
- \( \sin(x^2)y''-( \cos x)y'+x^2y=y'-3 \)
- \(y''+5xy'-3y= \cos y\)
Solución
- Esta ecuación es no lineal por el\(y^2\) término.
- Esta ecuación es lineal. No hay término que involucre una potencia o función de\(y,\) y los coeficientes son todas funciones\(x\) de.La ecuación ya está escrita en forma estándar, y\(r(x)\) es idénticamente cero, por lo que la ecuación es homogénea.
- Esta ecuación es no lineal. Obsérvese que, en este caso,\(x\) es la variable dependiente y\(t\) es la variable independiente. El segundo término involucra el producto de\(x\) y\(x'\), por lo que la ecuación es no lineal.
- Esta ecuación es lineal. Dado que\(r(x)=4x^5,\) la ecuación es no homogénea.
- Esta ecuación es no lineal, por el\(\sin y'\) término.
- Esta ecuación es lineal. Reescribirlo en forma estándar da
\[8t^2y''-6t^2y'+4ty=3t^2. \nonumber \]
Con la ecuación en forma estándar, podemos ver que\(r(t)=3t^2,\) así la ecuación es no homogénea. - Esta ecuación parece ser lineal, pero debemos reescribirla en forma estándar para estar seguros. Obtenemos
\[ \sin(x^2)y''-(\cos x+1)y'+x^2y=-3. \nonumber \]
Esta ecuación es, en efecto, lineal. Con\(r(x)=-3,\) ello no es homogéneo. - Esta ecuación es no lineal por el\(\cos y\) término.
Clasificar cada una de las siguientes ecuaciones como lineales o no lineales. Si la ecuación es lineal, determine además si es homogénea o no homogénea.
- \((y'')2-y'+8x^3y=0\)
- \((\sin t)y''+ \cos t-3ty'=0\)
- Insinuación
-
Escriba la ecuación en forma estándar (Ecuación\ ref {17.1}) si es necesario. Verificar poderes o funciones de\(y\) y sus derivados.
- Contestar a
-
Lineal no lineal
- Respuesta b
-
no homogéneo
Posteriormente en esta sección, veremos algunas técnicas para resolver tipos específicos de ecuaciones diferenciales. Antes de llegar a eso, sin embargo, vamos a tener una idea de cómo se comportan las soluciones a las ecuaciones diferenciales lineales. En muchos casos, resolver ecuaciones diferenciales depende de hacer conjeturas educadas sobre cómo podría ser la solución. Saber cómo se comportan los diversos tipos de soluciones será útil.
Considerar la ecuación diferencial lineal y homogénea
\[x^2y''-xy′-3y=0. \nonumber \]
Al observar esta ecuación, observe que las funciones de coeficiente son polinomios, con potencias superiores de\(x\) asociadas con derivadas de orden superior de\(y\). Mostrar que\(y=x^3\) es una solución a esta ecuación diferencial.
Solución
Dejar\(y=x^3.\) Entonces\(y'=3x^2\) y\(y''=6x.\) Sustituyendo en la ecuación diferencial, vemos que
\[\begin{align*} x^2y''-xy'-3y &=x^2(6x)-x(3x^2)-3(x^3) \\[4pt] &=6x^3-3x^3-3x^3 \\[4pt] &=0. \end{align*}\]
Mostrar que\(y=2x^2\) es una solución a la ecuación diferencial
\[\dfrac{1}{2}x^2y''-xy'+y=0. \label{ex2} \]
- Insinuación
-
Calcular las derivadas y sustituirlas en la ecuación diferencial.
- Contestar
-
Esto requiere calcular\(y'\) y\(y''\).
\[y' = \dfrac{dy}{dx} = 4x \nonumber \]
y
\[ y'' = \dfrac{dy'}{dx} = 4 \nonumber \]
Insertando estas derivadas junto con\(y=2x^2\) en la Ecuación\ ref {ex2}.
\[\begin{align*} \dfrac{1}{2}x^2y''-xy'+y &\overset{?}{=} 0 \\[4pt] \dfrac{1}{2}x^2(4) - x (4x) + 2x^2 &\overset{?}{=} 0 \\[4pt] 2x^2 - 4x^2 + 2x^2 &\overset{\checkmark}{=} 0 \end{align*} \nonumber \]
Sí, esta es una solución a la ecuación diferencial en la Ecuación\ ref {ex2}.
Aunque simplemente encontrar cualquier solución a una ecuación diferencial es importante, los matemáticos e ingenieros a menudo quieren ir más allá de encontrar una solución a una ecuación diferencial para encontrar todas las soluciones a una ecuación diferencial. Es decir, queremos encontrar una solución general. Al igual que con las ecuaciones diferenciales de primer orden, una solución general (o familia de soluciones) da todo el conjunto de soluciones a una ecuación diferencial. Una diferencia importante entre las ecuaciones de primer orden y de segundo orden es que, con las ecuaciones de segundo orden, normalmente necesitamos encontrar dos soluciones diferentes a la ecuación para encontrar la solución general. Si encontramos dos soluciones, entonces cualquier combinación lineal de estas soluciones también es una solución. Nosotros declaramos este hecho como el siguiente teorema.
Si\(y_1(x)\) y\(y_2(x)\) son soluciones a una ecuación diferencial homogénea lineal, entonces la función
\[y(x)=c_1y_1(x)+c_2y_2(x), \label{super} \]
donde\(c_1\) y\(c_2\) son constantes, también es una solución.
La prueba de este teorema del principio de superposición se deja como un ejercicio.
Considerar la ecuación diferencial
\[y''-4y'-5y=0.\nonumber \]
Dado que\(e^{-x}\) y\(e^{5x}\) son soluciones a esta ecuación diferencial, muestran que\(4e^{-x}+e^{5x}\) es una solución.
Solución
Aunque esto se puede hacer a través de una simple aplicación del principio de Superposición (Ecuación\ ref {super}), pero también podemos confirmar que es una solución a través de un enfoque como en Ejemplo\(\PageIndex{2}\). Tenemos
\[ \begin{align*} y(x) &=4e^{-x}+e^{5x} \\[4pt] y'(x) &= -4e^{-x} + 5e^{5x} \\[4pt] y''(x) &=4e^{-x}+25e^{5x}. \end{align*}\]
Entonces
\[\begin{align*} y''-4y'-5y &\overset{?}{=} (4e^{-x}+25e^{5x})-4(-4e^{-x}+5e^{5x})-5(4e^{-x}+e^{5x}) \\[4pt] &\overset{?}{=} 4e^{-x}+25e^{5x}+16e^{-x}-20e^{5x}-20e^{-x}-5e^{5x} \\[4pt] &\overset{\checkmark}{=}0. \end{align*} \nonumber \]
Así,\(y(x)=4e^{-x}+e^{5x}\) es una solución.
Considerar la ecuación diferencial
\[y''+5y'+6y=0. \nonumber \]
Dado que\(e^{-2x}\) y\(e^{-3x}\) son soluciones a esta ecuación diferencial, muestran que\(3e^{-2x}+6e^{-3x}\) es una solución.
- Insinuación
-
Diferenciar la función y sustituirla en la ecuación diferencial.
- Contestar
-
Aunque esto puede ser una simple aplicación del principio de Superposición (Ecuación\ ref {super}), también podemos establecer a través de él como en Ejemplo\(\PageIndex{2}\). Tenemos
\[ \begin{align*} y(x) &=3e^{-2x}+6e^{-3x} \\[4pt] y'(x) &= -6 e^{-2x} - 18e^{-3x} \\[4pt] y''(x) &= 12e^{-2x} + 54e^{3x}. \end{align*}\]
Entonces
\[\begin{align*} y''+5y'+6y &= (12e^{-2x} + 54e^{3x}) + 5( -6 e^{-2x} - 18e^{-3x} ) + 6( 3e^{-2x} + 6e^{3x}) \\[4pt] &\overset{?}{=} \cancel{12e^{-2x}} + \bcancel{54e^{3x}} - \cancel{30e^{-2x}} - \bcancel{90e^{3x}} + \cancel{18e^{-2x}} + \bcancel{36e^{3x}} \\[4pt] &\overset{\checkmark}{=}0. \end{align*} \nonumber \]
Así,\(3e^{-2x}+6e^{-3x}\) es una solución a la ecuación diferencial
Desafortunadamente, para encontrar la solución general a una ecuación diferencial de segundo orden, no basta con encontrar dos soluciones cualesquiera y luego combinarlas. Considerar la ecuación diferencial
\[x''+7x'+12x=0.\nonumber \]
Ambos\(e^{-3t}\) y\(2e^{-3t}\) son soluciones (puedes comprobarlo). Sin embargo,
\[x(t)=c_1e^{-3t}+c_2(2e^{-3t})\nonumber \]
no es la solución general. Esta expresión no da cuenta de todas las soluciones a la ecuación diferencial. En particular, no da cuenta de la función\(e^{-4t},\) que también es una solución a la ecuación diferencial. Resulta que para encontrar la solución general a una ecuación diferencial de segundo orden, debemos encontrar dos soluciones linealmente independientes. Aquí definimos esa terminología.
Se dice que un conjunto de funciones\(f_1(x),\, f_2(x), \ldots ,f_n(x)\) es linealmente dependiente si hay constantes\(c_1,\, c_2, \ldots c_n,\), no todas cero, tal que
\[c_1f_1(x)+c_2f_2(x)+ \cdots +c_nf_n(x)=0 \nonumber \]
para\(x\) todo el intervalo de interés. Se dice que un conjunto de funciones que no es linealmente dependiente es linealmente independiente.
En este capítulo, solemos probar conjuntos de sólo dos funciones para la independencia lineal, lo que nos permite simplificar esta definición. Desde una perspectiva práctica, vemos que dos funciones son linealmente dependientes si alguna de ellas es idéntica a cero o si son múltiplos constantes entre sí.
Primero mostramos que si las funciones cumplen con las condiciones dadas anteriormente, entonces son linealmente dependientes. Si una de las funciones es idéntica cero,\(f_2(x) \equiv 0\) digamos, entonces elige\(c_1=0\) y\(c_2=1,\) y se satisface la condición para la dependencia lineal. Si, por otro lado,\(f_1(x)\) ni tampoco\(f_2(x)\) es idénticamente cero, sino\(f_1(x)=Cf_2(x)\) para alguna constante\(C,\) entonces elige\(c_1=C\) y\(c_2=-1,\) y otra vez, se satisface la condición.
A continuación, mostramos que si dos funciones son linealmente dependientes, entonces o una es idéntica a cero o son múltiplos constantes entre sí. Asumir\(f_1(x)\) y\(f_2(x)\) son linealmente independientes. Entonces, hay constantes,\(c_1\) y\(c_2,\) no ambas cero, tal que
\[c_1f_1(x)+c_2f_2(x)=0 \nonumber \]
para\(x\) todo el intervalo de interés. Entonces,
\[c_1f_1(x)=-c_2f_2(x). \nonumber \]
Ahora bien, ya que dijimos que\(c_1\) y no\(c_2\) pueden ser ambos cero, supongamos\(c_2 \neq 0.\) Entonces, hay dos casos: cualquiera\(c_1=0\) o\(c_1\neq 0.\) Si\(c_1=0,\) entonces
\[\begin{align*} 0 &=-c_2f_2(x) \\[4pt] 0 &=f_2(x), \end{align*}\]
así que una de las funciones es idéntica a cero. Ahora supongamos\(c_1 \neq 0.\) Entonces,
\[f_1(x)=\left(- \dfrac{c_2}{c_1}\right)f_2(x) \nonumber \]
y vemos que las funciones son múltiplos constantes entre sí.
Dos funciones,\(f_1(x)\) y\(f_2(x),\) se dice que son linealmente dependientes si alguna de ellas es idéntica a cero o si\(f_1(x)=Cf_2(x)\) para alguna constante\(C\) y para\(x\) todo el intervalo de interés. Se dice que las funciones que no son linealmente dependientes son linealmente independientes.
Determinar si los siguientes pares de funciones son linealmente dependientes o linealmente independientes.
- \(f_1(x)=x^2\)y\(f_2(x)=5x^2\)
- \(f_1(x)= \sin x\)y\(f_2(x)= \cos x\)
- \(f_1(x)=e^{3x}\)y\(f_2(x)=e^{-3x}\)
- \(f_1(x)=3x\)y\(f_2(x)=3x+1\)
Solución
- \(f_2(x)=5f_1(x),\)por lo que las funciones son linealmente dependientes.
- No hay constante\(C\) tal que\(f_1(x)=Cf_2(x),\) así las funciones sean linealmente independientes.
- No hay constante\(C\) tal que\(f_1(x)=Cf_2(x),\) así las funciones sean linealmente independientes. No te confundas por el hecho de que los exponentes son múltiplos constantes entre sí. Con dos funciones exponenciales, a menos que los exponentes sean iguales, las funciones son linealmente independientes.
- No hay constante\(C\) tal que\(f_1(x)=Cf_2(x),\) así las funciones sean linealmente independientes.
Determine si los siguientes pares de funciones son linealmente dependientes o linealmente independientes:\(f_1(x)=e^{x}\) y\(f_2(x)=3e^{3x}.\)
- Pista
-
¿Las funciones son múltiplos constantes entre sí?
- Contestar
-
Linealmente independiente
Si somos capaces de encontrar dos soluciones linealmente independientes a una ecuación diferencial de segundo orden, entonces podemos combinarlas para encontrar la solución general. Este resultado se expresa formalmente en el siguiente teorema.
Si\(y_1(x)\) y\(y_2(x)\) son soluciones linealmente independientes a una ecuación diferencial homogénea de segundo orden, lineal, entonces la solución general viene dada por
\[y(x)=c_1y_1(x)+c_2y_2(x), \nonumber \]
donde\(c_1\) y\(c_2\) son constantes.
Cuando decimos que una familia de funciones es la solución general a una ecuación diferencial, queremos decir que
- cada expresión de esa forma es una solución y
- cada solución a la ecuación diferencial se puede escribir en esa forma, lo que hace que este teorema sea extremadamente poderoso.
Si podemos encontrar dos soluciones linealmente independientes para una ecuación diferencial de segundo orden, efectivamente hemos encontrado todas las soluciones a la ecuación diferencial de segundo orden, una afirmación bastante notable. La prueba de este teorema está fuera del alcance de este texto.
Si\(y_1(t)=e^{3t}\) y\(y_2(t)=e^{-3t}\) son soluciones a\(y''-9y=0,\) cual es la solución general?
Solución
Tenga en cuenta que\(y_1\) y no\(y_2\) son múltiplos constantes entre sí, por lo que son linealmente independientes. Entonces, la solución general a la ecuación diferencial es
\(y(t)=c_1e^{3t}+c_2e^{-3t}.\)
Si\(y_1(x)=e^{3x}\) y\(y_2(x)=xe^{3x}\) son soluciones a\(y''-6y'+9y=0,\) cual es la solución general?
- Pista
-
Verifique primero la independencia lineal.
- Contestar
-
\(y(x)=c_1e^{3x}+c_2xe^{3x}\)
Ecuaciones de segundo orden con coeficientes constantes
Ahora que tenemos una mejor idea de las ecuaciones diferenciales lineales, nos vamos a concentrar en resolver ecuaciones de segundo orden de la forma
\[ay''+by'+cy=0, \tag{17.2} \]
donde\(a, b,\) y\(c\) son constantes.
Dado que todos los coeficientes son constantes, las soluciones probablemente van a ser funciones con derivadas que son múltiplos constantes de sí mismas. Necesitamos todos los términos para cancelar, y si tomar un derivado introduce un término que no es un múltiplo constante de la función original, es difícil ver cómo se cancela ese término. Las funciones exponenciales tienen derivadas que son múltiplos constantes de la función original, así que veamos qué sucede cuando intentamos una solución de la forma\(y(x)=e^{ \lambda x}\), donde\(\lambda\) (la letra griega minúscula lambda) es alguna constante.
Si\(y(x)=e^{ \lambda x}\), entonces\(y'(x)= \lambda e^{ \lambda x}\) y\(y''= \lambda^2 e^{ \lambda x}.\) Sustituyendo estas expresiones en la Ecuación\ ref {17.1}, obtenemos
\[\begin{align*} ay''+by'+cy &= a(\lambda^2e^{\lambda x})+b(\lambda e^{\lambda x})+ce^{\lambda x} \\[4pt] &=e^{\lambda x}(a \lambda^2+b \lambda +c). \end{align*}\]
Como nunca\(e\lambda x\) es cero, esta expresión puede ser igual a cero para todos\(x\) solo si
\[a\lambda 2+b\lambda +c=0. \nonumber \]
A esto lo llamamos la ecuación característica de la ecuación diferencial.
La ecuación característica de la ecuación diferencial de segundo orden\(ay''+by'+cy=0\) es
\[a\lambda^2+b\lambda +c=0. \nonumber \]
La ecuación característica es muy importante para encontrar soluciones a ecuaciones diferenciales de esta forma. Podemos resolver la ecuación característica ya sea factorizando o usando la fórmula cuadrática
\[\lambda = \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}. \nonumber \]
Esto da tres casos. La ecuación característica tiene
- raíces reales distintas;
- una sola raíz real repetida; o
- raíces conjugadas complejas.
Consideramos cada uno de estos casos por separado.
Caso 1: Raíces Reales Distintas
Si la ecuación característica tiene raíces reales distintas\(\lambda_1\) y\(\lambda_2\), entonces\(e^{\lambda_1x}\) y\(e^{\lambda_2x}\) son soluciones linealmente independientes al Ejemplo\ ref {17.1}, y la solución general viene dada por
\[y(x)=c_1e^{\lambda_1x}+c_2e^{\lambda_2x}, \nonumber \]
donde\(c_1\) y\(c_2\) son constantes.
Por ejemplo, la ecuación diferencial\(y''+9y'+14y=0\) tiene la ecuación característica asociada\(\lambda^2+9\lambda+14=0.\) Estos factores en los\((\lambda +2)(\lambda +7)=0,\) que tiene raíces\(\lambda_1=-2\) y\(\lambda_2=-7.\) Por lo tanto, la solución general a esta ecuación diferencial es
\[y(x)=c_1e^{-2x}+c_2e^{-7x}. \nonumber \]
Caso 2: Raíz Real Repetida Única
Las cosas son un poco más complicadas si la ecuación característica tiene una raíz real repetida,\(\lambda\). En este caso, sabemos que\(e^{\lambda x}\) es una solución a la Ecuación\ ref {17.1}, pero es sólo una solución y necesitamos dos soluciones linealmente independientes para determinar la solución general. Podríamos tener la tentación de probar una función de la forma\(ke^{\lambda x},\) donde\(k\) hay alguna constante, pero no sería linealmente independiente de\(e^{\lambda x}.\) Por lo tanto, intentemos\(xe^{\lambda x}\) como la segunda solución. Primero, tenga en cuenta que por la fórmula cuadrática,
\[\lambda = \frac{-b \pm \sqrt{b^2-4ac}}{2a}. \nonumber \]
Pero,\(\lambda\) es una raíz repetida, por lo que el discriminate (\(b^2-4ac\)) es cero y\(\lambda = \frac{-b}{2a}\). Por lo tanto\(y=xe^{\lambda x}\), si, tenemos
\[\begin{align*} y' =e^{\lambda x}+ \lambda xe^{\lambda x} \\[4pt] y'' =2\lambda e^{\lambda x}+\lambda^2xe^{\lambda x}. \end{align*}\]
Sustituyendo ambas expresiones en la Ecuación\ ref {17.1}, vemos que
\[\begin{align*} ay''+by′+cy &=a(2λe^{λx}+λ^2xe^{λx})+b(e^{λx}+λxe^{λx})+cxe^{λx} \\[4pt] &=xe^{λx}(aλ^2+bλ+c)+e^{λx}(2aλ+b) \\[4pt] &=xe^{λx}(0)+e^{λx}(2a(−b2a)+b)\\[4pt] &=0+e^{λx}(0) \\[4pt] &\overset{\checkmark}{=}0. \end{align*}\]
Esto demuestra que\(xe^{\lambda x}\) es una solución a la Ecuación\ ref {17.1}. Dado que\(e^{\lambda x}\) y\(xe^{\lambda x}\) son linealmente independientes, cuando la ecuación característica tiene una raíz repetida\(\lambda \), la solución general a la Ecuación\ ref {17.1} viene dada por
\[y(x)=c_1e^{\lambda x}+c_2xe^{\lambda x}, \nonumber \]
donde\(c_1\) y\(c_2\) son constantes.
Por ejemplo, la ecuación diferencial\(y''+12y'+36y=0\) tiene la ecuación característica asociada
\[\lambda^2+12 \lambda +36=0.\nonumber \]
Esto factores en los\((\lambda +6)^2=0,\) que tiene una raíz repetida\(\lambda =-6\). Por lo tanto, la solución general a esta ecuación diferencial es
\[y(x)=c_1e^{-6x}+c_2xe^{-6x}.\nonumber \]
Caso 3: Raíces Conjugadas Complejas
El tercer caso que debemos considerar es cuando\(b^2-4ac <0.\) En este caso, cuando aplicamos la fórmula cuadrática, estamos tomando la raíz cuadrada de un número negativo. Debemos usar el número imaginario\( i= \sqrt{-1}\) para encontrar las raíces, que toman la forma\(\lambda_1= \alpha + \beta i \) y\(\lambda _2=\alpha -\beta i.\) El número complejo\( \alpha +\beta i\) se llama el conjugado de\( \alpha -\beta i\). Así, vemos que cuando el discriminado\(b^2-4ac\) es negativo, las raíces de nuestra ecuación característica son siempre conjugados complejos.
Esto nos crea un pequeño problema. Si seguimos el mismo proceso que usamos para distintas raíces reales —usando las raíces de la ecuación característica como los coeficientes en los exponentes de las funciones exponenciales— obtenemos las funciones\(e^{(\alpha + \beta i)x}\) y\(e^{(\alpha - \beta i)x}\) como nuestras soluciones. No obstante, hay problemas con este enfoque. En primer lugar, estas funciones toman valores complejos (imaginarios), y una discusión completa de tales funciones está fuera del alcance de este texto. Segundo, aunque estuviéramos cómodos con las funciones de valor complejo, en este curso no abordamos la idea de un derivado para tales funciones. Entonces, si es posible, nos gustaría encontrar dos soluciones de valor real linealmente independientes para la ecuación diferencial. Para fines de este desarrollo, vamos a manipular y diferenciar las funciones\(e^{(\alpha + \beta i)x}\) y\(e^{(\alpha - \beta i)x}\) como si fueran funciones de valor real. Para estas funciones particulares, este enfoque es válido matemáticamente, pero tenga en cuenta que hay otras instancias en las que las funciones de valor complejo no siguen las mismas reglas que las funciones de valor real. Aquellos de ustedes interesados en una discusión más profunda de las funciones de valor complejo deben consultar un texto de análisis complejo.
Con base en las raíces\(\alpha \pm \beta i\) de la ecuación característica, las funciones\(e^{(\alpha + \beta i)x}\) y\(e^{(\alpha - \beta i)x}\) son soluciones linealmente independientes a la ecuación diferencial y la solución general viene dada por
\[y(x)=c_1e^{(\alpha +\beta i)x}+c_2e^{(\alpha - \beta i)x}. \nonumber \]
Usando algunas opciones inteligentes para\(c_1\) y\(c_2\), y un poco de manipulación algebraica, podemos encontrar dos soluciones linealmente independientes de valor real para la Ecuación\ ref {17.1} y expresar nuestra solución general en esos términos.
Anteriormente encontramos funciones exponenciales con exponentes complejos. Una de las herramientas clave que utilizamos para expresar estas funciones exponenciales en términos de senos y cosenos fue la fórmula de Euler, que nos dice que
\[\underbrace{e^{i \theta }= \cos \theta+ i \sin \theta}_{\text{Euler’s formula}} \label{Euler} \]
para todos los números reales\(\theta \).
Volviendo a la solución general, tenemos
\[\begin{align*} y(x) &=c_1e^{( \alpha+ \beta i)x}+c_2e^{(\alpha - \beta i)x} \\[4pt] &=c_1e^{\alpha x}e^{\beta ix}+c_2e^{\alpha x}e^{- \beta ix} \\[4pt] &=e^{\alpha x}(c_1e^{\beta ix}+c_2e^{-\beta ix}).\end{align*}\]
Aplicando la fórmula de Euler (Ecuación\ ref {Euler}) junto con las identidades\(\cos(-x)=\cos x\) y\(\sin(-x)=- \sin x,\) obtenemos
\[\begin{align} y(x) &=e^{\alpha x}[c_1(\cos \beta x+i \sin \beta x)+c_2(\cos(- \beta x)+i \sin(- \beta x))] \nonumber \\[4pt] &=e^{\alpha x}[(c_1+c_2)\cos \beta x+(c_1-c_2)i \sin \beta x]. \label{E1}\end{align} \]
Ahora, si elegimos\(c_1=c_2= \frac{1}{2},\) el segundo término es cero y obtenemos
\[y(x)=e^{\alpha x} \cos \beta x \nonumber \]
como una solución de valor real a la Ecuación\ ref {17.1}. Del mismo modo, si elegimos\(c_1=−\frac{i}{2}\) y\(c_2=\frac{i}{2}\), el primer término de la Ecuación\ ref {E1} es cero y obtenemos
\[y(x)=e^{\alpha x} \sin \beta x \nonumber \]
como una segunda solución linealmente independiente de valor real a la Ecuación\ ref {17.1}.
En base a esto, vemos que si la ecuación característica tiene raíces conjugadas complejas\(\alpha \pm \beta i,\) entonces la solución general a la Ecuación\ ref {17.1} viene dada por
\[\begin{align*} y(x) &=c_1e^{\alpha x} \cos \beta x+c_2e^{\alpha x} \sin \beta x \\[4pt] &=e^{\alpha x}(c_1 \cos \beta x+c_2 \sin \beta x),\end{align*}\]
donde\(c_1\) y\(c_2\) son constantes.
Por ejemplo, la ecuación diferencial\(y''-2y'+5y=0\) tiene la ecuación característica asociada\(\lambda ^2-2 \lambda +5=0.\) Por la fórmula cuadrática, las raíces de la ecuación característica son\(1\pm 2i.\) Por lo tanto, la solución general a esta ecuación diferencial es
\[y(x)=e^{x}(c_1 \cos 2x+c_2 \sin 2x).\nonumber \]
Resumen de resultados
Podemos resolver ecuaciones diferenciales homogéneas, lineales y de segundo orden con coeficientes constantes, encontrando las raíces de la ecuación característica asociada. La forma de la solución general varía, dependiendo de si la ecuación característica tiene raíces distintas, reales; una sola raíz real repetida; o raíces conjugadas complejas. Los tres casos se resumen en la Tabla\(\PageIndex{1}\).
| Ecuación característica Raíces | Solución General a la Ecuación Diferencial |
|---|---|
| Distintas raíces reales,\(\lambda_1\) y\(\lambda_2\) | \(y(x)=c_1e^{\lambda_1x}+c_2e^{\lambda_2x}\) |
| Una raíz real repetida,\(\lambda \) | \(y(x)=c_1e^{\lambda x}+c_2xe^{\lambda x}\) |
| Raíces conjugadas complejas\(\alpha \pm \beta i\) | \(y(x)=e^{\alpha x}(c_1 \cos \beta x+c_2 \sin \beta x)\) |
- Escribe la ecuación diferencial en la forma\(a''+by'+cy=0.\)
- Encuentra la ecuación característica correspondiente\(a\lambda^2+b\lambda +c=0.\)
- O factorial la ecuación característica o usa la fórmula cuadrática para encontrar las raíces.
- Determinar la forma de la solución general en función de si la ecuación característica tiene raíces distintas, reales; una sola raíz real repetida; o raíces conjugadas complejas.
Encuentre la solución general a las siguientes ecuaciones diferenciales. Da tus respuestas como funciones de\(x\).
- \(y''+3y'-4y=0\)
- \(y''+6y'+13y=0\)
- \(y''+2y'+y=0\)
- \(y''-5y'=0\)
- \(y''-16y=0\)
- \(y''+16y=0\)
Solución
Tenga en cuenta que todas estas ecuaciones ya se dan en forma estándar (paso 1).
- La ecuación característica es\(\lambda^2+3\lambda -4=0\) (paso 2). Esto influye en\((\lambda +4)(\lambda -1)=0\), por lo que las raíces de la ecuación característica son\(\lambda_1=-4\) y\(\lambda_2=1\) (paso 3). Entonces la solución general a la ecuación diferencial es
\[y(x)=c_1e^{-4x}+c_2e^{x}. \tag{step 1} \]
- La ecuación característica es\(\lambda^2+6\lambda+13=0\) (paso 2). Aplicando la fórmula cuadrática, vemos que esta ecuación tiene raíces conjugadas complejas\(-3\pm 2i\) (paso 3). Entonces la solución general a la ecuación diferencial es
\[y(t)=e^{-3t}(c_1 \cos 2t+c_2 \sin 2t). \tag{step 2} \]
- La ecuación característica es\(\lambda^2+2\lambda+1=0\) (paso 2). Esto influye en\((\lambda+1)2=0,\) que la ecuación característica tiene una raíz real repetida\(\lambda =-1\) (paso 3). Entonces la solución general a la ecuación diferencial es
\[y(t)=c_1e^{-t}+c_2te^{-t}. \tag{step 3} \]
- La ecuación característica es\(\lambda^2-5\lambda\) (paso 2). Esto influye en\(\lambda(\lambda -5)=0,\) así que las raíces de la ecuación característica son\(\lambda_1=0\) y\(\lambda_2=5\) (paso 3). Tenga en cuenta que\(e^{0x}=e^{0}=1\), por lo que nuestra primera solución es solo una constante. Entonces la solución general a la ecuación diferencial es
\[y(x)=c_1+c_2e^{5x}. \tag{step 4} \]
- La ecuación característica es\(\lambda^2-16=0\) (paso 2). Esto influye en\((\lambda+4)(\lambda -4)=0,\) así que las raíces de la ecuación característica son\(\lambda_1=4\) y\(\lambda_2=-4\) (paso 3). Entonces la solución general a la ecuación diferencial es
\[y(x)=c_1e^{4x}+c_2e^{-4x}. \tag{step 5} \]
- La ecuación característica es\(\lambda^2+16=0\) (paso 2). Esto tiene raíces conjugadas complejas\(\pm 4i\) (paso 3). Tenga en cuenta que\(e^{0x}=e^0=1\), por lo que el término exponencial en nuestra solución es solo una constante. Entonces la solución general a la ecuación diferencial es
\[y(t)=c_1 \cos 4t+c_2 \sin 4t. \tag{step 6} \]
Encuentre la solución general a las siguientes ecuaciones diferenciales:
- \(y''-2y'+10y=0\)
- \(y''+14y'+49y=0\)
- Pista
-
Encuentra las raíces de la ecuación característica.
- Contestar a
-
\(y(x)=e^x(c_1 \cos 3x+c_2 \sin 3x)\)
- Respuesta b
-
\(y(x)=c_1e^{-7x}+c_2xe^{-7x}\)
Problemas de Valor Inicial y Problemas de Valor Límite
Hasta el momento, hemos estado encontrando soluciones generales a las ecuaciones diferenciales. Sin embargo, las ecuaciones diferenciales se utilizan a menudo para describir sistemas físicos, y la persona que estudia ese sistema físico suele saber algo sobre el estado de ese sistema en uno o más momentos en el tiempo. Por ejemplo, si una ecuación diferencial de coeficiente constante representa hasta qué punto se comprime un amortiguador de motocicleta, podríamos saber que el piloto está sentado quieto en su motocicleta al inicio de una carrera, tiempo\(t=t_0.\) Esto significa que el sistema está en equilibrio, entonces\(y(t_0)=0,\) y la compresión de el amortiguador no está cambiando, así que\(y'(t_0)=0.\) con estas dos condiciones iniciales y la solución general a la ecuación diferencial, podemos encontrar la solución específica a la ecuación diferencial que satisfaga ambas condiciones iniciales. Este proceso se conoce como resolver un problema de valor inicial. (Recordemos que discutimos problemas de valor inicial en Introducción a las Ecuaciones Diferenciales.) Tenga en cuenta que las ecuaciones de segundo orden tienen dos constantes arbitrarias en la solución general, y por lo tanto requerimos dos condiciones iniciales para encontrar la solución al problema del valor inicial.
A veces conocemos la condición del sistema en dos momentos diferentes. Por ejemplo, podríamos saber\(y(t_0)=y_0\) y\(y(t_1)=y_1.\) Estas condiciones se denominan condiciones de límite, y encontrar la solución a la ecuación diferencial que satisface las condiciones límite se llama resolver un problema de valor límite.
Los matemáticos, científicos e ingenieros están interesados en comprender las condiciones bajo las cuales un problema de valor inicial o un problema de valor límite tiene una solución única. Si bien un tratamiento completo de este tema está fuera del alcance de este texto, es útil saber que, en el contexto de las ecuaciones de segundo orden de coeficiente constante, se garantiza que los problemas de valor inicial tengan una solución única siempre y cuando se proporcionen dos condiciones iniciales. Sin embargo, los problemas de valor límite no se comportan tan bien. Incluso cuando se conocen dos condiciones de límite, podemos encontrar problemas de valor límite con soluciones únicas, muchas soluciones o ninguna solución en absoluto.
Resuelve el siguiente problema de valor inicial:\(y''+3y'-4y=0, \, y(0)=1,\, y'(0)=-9.\)
Solución
Ya resolvimos esta ecuación diferencial en el Ejemplo 17.6a. y encontramos que la solución general era
\[y(x)=c_1e^{-4x}+c_2e^{x}. \nonumber \]
Entonces
\[y'(x)=-4c_1e^{-4x}+c_2e^{x}. \nonumber \]
Cuando\(x=0,\) tenemos\(y(0)=c_1+c_2\) y\(y'(0)=-4c_1+c_2.\) Aplicando las condiciones iniciales, tenemos
\[\begin{align*} c_1+c_2 &=1 \\[4pt] -4c_1+c_2 &=-9.\end{align*}\]
Después,\(c_1=1-c_2.\) sustituyendo esta expresión en la segunda ecuación, vemos que
\[\begin{align*} -4(1-c_2)+c_2 &= -9 \\[4pt] -4+4c_2+c_2 &=-9 \\[4pt] 5c_2 &=-5 \\[4pt] c_2 &=-1. \end{align*}\]
Entonces,\(c_1=2\) y la solución al problema del valor inicial es
\[y(x)=2e^{-4x}-e^{x}. \nonumber \]
Resolver el problema del valor inicial\(y''-3y'-10y=0, \quad y(0)=0, \; y'(0)=7.\)
- Pista
-
Utilice las condiciones iniciales para determinar valores para\(c_1\) y\(c_2\).
- Contestar
-
\[y(x)=-e^{-2x}+e^{5x} \nonumber \]
Resuelva el siguiente problema de valor inicial y grafique la solución:
\[y''+6y'+13y=0, \quad y(0)=0, \; y'(0)=2\nonumber \]
Solución
Ya resolvimos esta ecuación diferencial en Ejemplo\(\PageIndex{6b}\). y encontramos que la solución general era
\[y(x)=e^{-3x}(c_1 \cos 2x+c_2 \sin 2x).\nonumber \]
Entonces
\[y'(x)=e^{-3x}(-2c_1 \sin 2x+2c_2 \cos 2x)-3e^{-3x}(c_1 \cos 2x+c_2 \sin 2x). \nonumber \]
Cuando\(x=0,\) tenemos\(y(0)=c_1\) y\(y'(0)=2c_2-3c_1\). Aplicando las condiciones iniciales, obtenemos
\[ \begin{align*} c_1 &=0 \\[4pt] -3c_1+2c_2 &=2. \end{align*}\]
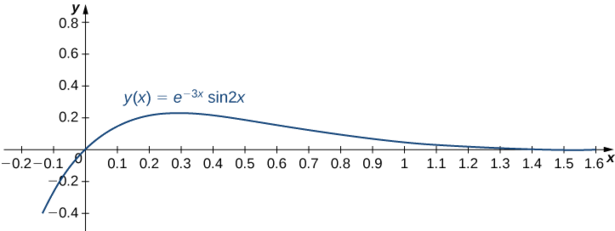
Por lo tanto,\(c_1=0, \, c_2=1,\) y la solución al problema de valor inicial se muestra en la siguiente gráfica.
\[y=e^{-3x} \sin 2x.\nonumber \]
Resuelva el siguiente problema de valor inicial y grafique la solución:\(y''-2y'+10y=0, \quad y(0)=2, \; y'(0)=-1\)
- Pista
-
Utilice las condiciones iniciales para determinar valores para\(c_1\) y\(c_2.\)
- Contestar
-
\[y(x)=e^{x}(2 \cos 3x - \sin 3x) \nonumber \]
El siguiente problema de valor inicial modela la posición de un objeto con masa unida a un resorte. Los sistemas de masa de resorte se examinan en detalle en Aplicaciones. La solución a la ecuación diferencial da la posición de la masa con respecto a una posición neutra (equilibrio) (en metros) en cualquier momento dado. (Tenga en cuenta que para los sistemas de masa de resorte de este tipo, se acostumbra definir la dirección hacia abajo como positiva).
\[y''+2y'+y=0, \quad y(0)=1, \; y'(0)=0 \nonumber \]
Resuelve el problema del valor inicial y grafica la solución. ¿Cuál es la posición de la masa en el tiempo\(t=2\) sec? ¿Qué tan rápido se mueve la masa en el tiempo\(t=1\) sec? ¿En qué dirección?
Solución
En Ejemplo Ejemplo\(\PageIndex{6c}\). encontramos que la solución general a esta ecuación diferencial es
\[y(t)=c_1e^{-t}+c_2te^{-t}. \nonumber \]
Entonces
\[y'(t)=-c_1e^{-t}+c_2(-te^{-t}+e^{-t}). \nonumber \]
Cuando\(t=0,\) tenemos\(y(0)=c_1\) y\(y'(0)=c_1+c_2.\) Aplicando las condiciones iniciales, obtenemos
\[c_1=1 \\ -c_1+c_2=0. \nonumber \]
Así,\(c_1=1, c_2=1,\) y la solución al problema del valor inicial es
\[y(t)=e^{-t}+te^{-t}. \nonumber \]
Esta solución se representa en la siguiente gráfica. En\(t=2,\) el momento la masa se encuentra en la posición\(y(2)=e^{-2}+2e^{-2}=3e^{-2} \approx 0.406\) m por debajo del equilibrio.
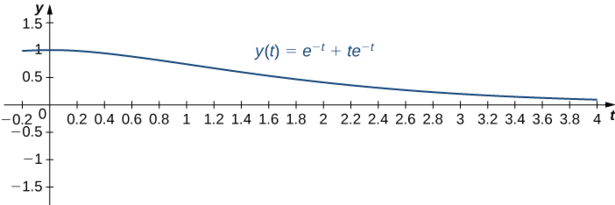
Para calcular la velocidad en el momento\(t=1,\) necesitamos encontrar la derivada. Tenemos\(y(t)=e^{-t}+te^{-t},\) tan
\[y'(t)=-e^{-t}+e^{-t}-te^{-t}= -te^{-t}. \nonumber \]
Entonces\(y'(1)=-e^{-1} \approx -0.3679\). En\(t=1,\) el momento la masa se mueve hacia arriba a\(0.3679\) m/seg.
Supongamos que el siguiente problema de valor inicial modela la posición (en pies) de una masa en un sistema de masa de resorte en un momento dado. Resuelve el problema del valor inicial y grafica la solución. ¿Cuál es la posición de la masa en el tiempo\(t=0.3\) sec? ¿Qué tan rápido se mueve en el tiempo\(t=0.1\) sec? ¿En qué dirección?
\[y''+14y'+49y=0, \quad y(0)=0, \; y'(0)=1 \nonumber \]
- Pista
-
Utilice las condiciones iniciales para determinar valores para\(c_1\) y\(c_2\).
- Contestar
-
\[y(t)=te^{-7t}\nonumber \]
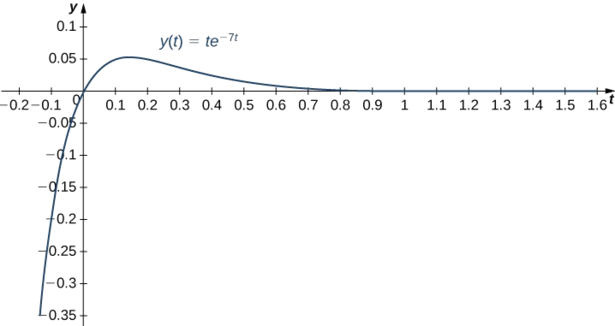
En\(t=0.3, \; y(0.3)=0.3e^{(-7^{\ast} 0.3)}=0.3e^{-2.1} \approx 0.0367. \) el tiempo La masa está\(0.0367\) ft por debajo del equilibrio. En\(t=0.1, \; y'(0.1)=0.3e^{-0.7} \approx 0.1490.\) el momento La masa se mueve hacia abajo a una velocidad de\(0.1490\) pies/seg.
En el Ejemplo 17.6f. resolvimos la ecuación diferencial\(y''+16y=0\) y encontramos que la solución general era\(y(t)=c_1 \cos 4t+c_2 \sin 4t.\) Si es posible, resolver el problema del valor límite si las condiciones límite son las siguientes:
- \(y(0)=0, y( \frac{\pi}{4})=0\)
- \(y(0)=1,y(0)=1, y(\frac{\pi}{8})=0\)
- \(y(\frac{\pi}{8})=0, y(\frac{3 \pi}{8})=2\)
Solución
Tenemos
\[y(x)=c_1 \cos 4t+c_2 \sin 4t. \nonumber \]
- Aplicando la primera condición de límite dada aquí, obtenemos\(y(0)=c_1=0.\) Así que la solución es de la forma\(y(t)=c_2 \sin 4t.\) Cuando aplicamos la segunda condición de límite, sin embargo, obtenemos\(y(\frac{\pi}{4})=c_2 \sin(4(\frac{\pi}{4}))=c_2 \sin \pi =0 \) para todos los valores de\(c_2\). Las condiciones límite no son suficientes para determinar un valor por\(c_2,\) lo que este problema de valor límite tiene infinitamente muchas soluciones. Así,\(y(t)=c_2 \sin 4t\) es una solución para cualquier valor de\(c_2\).
- Aplicando la primera condición de límite dada aquí, obtenemos\(y(0)=c_1=1.\) Aplicando la segunda condición de límite da\(y(\frac{\pi}{8})=c_2=0,\) así\(c_2=0.\) En este caso, tenemos una solución única:\(y(t)= \cos 4t\).
- Aplicando la primera condición de límite dada aquí, obtenemos\(y(\frac{\pi}{8})=c_2=0.\) Sin embargo, aplicar la segunda condición de límite da\(y(\frac{3 \pi}{8})=-c_2=2,\) así que no\(c_2=-2.\) podemos tener\(c_2=0=-2,\) por lo que este problema de valor límite no tiene solución.
Conceptos clave
- Las ecuaciones diferenciales de segundo orden pueden clasificarse como lineales o no lineales, homogéneas o no homogéneas.
- Para encontrar una solución general para una ecuación diferencial homogénea de segundo orden, debemos encontrar dos soluciones linealmente independientes. Si\(y_1(x)\) y\(y_2(x)\) son soluciones linealmente independientes a una ecuación diferencial homogénea de segundo orden, lineal, entonces la solución general viene dada por
\[y(x)=c_1y_1(x)+c_2y_2(x).\nonumber \]
- Para resolver ecuaciones diferenciales homogéneas de segundo orden con coeficientes constantes, encuentre las raíces de la ecuación característica. La forma de la solución general varía dependiendo de si la ecuación característica tiene raíces distintas, reales; una sola raíz real repetida; o raíces conjugadas complejas.
- Las condiciones iniciales o condiciones de límite se pueden usar entonces para encontrar la solución específica a una ecuación diferencial que satisfaga esas condiciones, excepto cuando no hay solución o infinitamente muchas soluciones.
Ecuaciones Clave
- Ecuación diferencial lineal de segundo orden\[a_2(x)y''+a_1(x)y'+a_0(x)y=r(x) \nonumber \]
- Ecuación de segundo orden con coeficientes constantes\[ay''+by'+cy=0 \nonumber \]
Glosario
- condiciones de contorno
- las condiciones que dan el estado de un sistema en diferentes momentos, como la posición de un sistema de masa de resorte en dos momentos diferentes
- problema de valor límite
- una ecuación diferencial con condiciones de límite asociadas
- ecuación característica
- la ecuación\(aλ^2+bλ+c=0\) para la ecuación diferencial\(ay″+by′+cy=0\)
- ecuación lineal homogénea
- una ecuación diferencial de segundo orden que se puede escribir en la forma\(a_2(x)y″+a_1(x)y′+a_0(x)y=r(x)\), pero\(r(x)=0\) por cada valor de\(x\)
- ecuación lineal no homogénea
- una ecuación diferencial de segundo orden que se puede escribir en la forma\(a_2(x)y″+a_1(x)y′+a_0(x)y=r(x)\), pero\(r(x)≠0\) para algún valor de\(x\)
- linealmente dependiente
- un conjunto de funciones\(f_1(x),\,f_2(x),\,…,\,f_n(x)\) para las cuales hay constantes\(c_1,\,c_2,\,…,\,c_n\), no todas cero, tal que\(c_1f_1(x)+c_2f_2(x)+⋯+c_nf_n(x)=0\) para todos\(x\) en el intervalo de interés
- linealmente independiente
- un conjunto de funciones\(f_1(x),\,f_2(x),\,…,\,f_n(x)\) para las que no hay constantes\(c_1,\,c_2,\,…,\,c_n\), tal que\(c_1f_1(x)+c_2f_2(x)+⋯+c_nf_n(x)=0\) para todos\(x\) en el intervalo de interés