1.4: Funciones inversas

Objetivos de aprendizaje

• Determinar las condiciones para cuando una función tiene una inversa.
• Utilice la prueba de línea horizontal para reconocer cuando una función es uno a uno.
• Encuentra la inversa de una función dada.
• Dibuja la gráfica de una función inversa.
• Evaluar funciones trigonométricas inversas.

Una función inversa invierte la operación realizada por una función particular. En otras palabras, haga lo que haga una función, la función inversa la deshace. En esta sección, definimos formalmente una función inversa y declaramos las condiciones necesarias para que exista una función inversa. Examinamos cómo encontrar una función inversa y estudiar la relación entre la gráfica de una función y la gráfica de su inversa. Luego aplicamos estas ideas para definir y discutir las propiedades de las funciones trigonométricas inversas.

Existencia de una función inversa

Comenzamos con un ejemplo. Dada una función\(f\) y una salida\(y=f(x)\), a menudo nos interesa encontrar qué valor o valores\(x\) fueron mapeados\(y\) por\(f\). Por ejemplo, considere la función\(f(x)=x^3+4\). Desde cualquier salida\(y=x^3+4\), podemos resolver esta ecuación\(x\) para encontrar que la entrada es\(x=\sqrt[3]{y−4}\). Esta ecuación define\(x\) como una función de\(y\). Denotando esta función como\(f^{−1}\), y escribiendo\(x=f^{−1}(y)=\sqrt[3]{y−4}\), vemos que para cualquiera\(x\) en el dominio de\(f,f^{−1}\)\(f(x))=f^{−1}(x^3+4)=x\). Así, esta nueva función,\(f^{−1}\), “deshizo” lo que\(f\) hacía la función original. Una función con esta propiedad se llama la función inversa de la función original.

Definición: Funciones inversas

Dada una función\(f\) con dominio\(D\) y rango\(R\), su función inversa (si existe) es la función\(f^{−1}\) con dominio\(R\) y rango\(D\) tal que\(f^{−1}(y)=x\) si y solo si\(f(x)=y\). En otras palabras, para una función\(f\) y su inversa\(f^{−1}\),

\[f^{−1}(f(x))=x \nonumber \]

para todos\(x\) en\(D\) y

\[f(f^{−1}(y))=y \nonumber \]

para todos\(y\) en\(R\).

Tenga en cuenta que\(f^{−1}\) se lee como “\(f\)inverso”. Aquí, el no\(−1\) se utiliza como exponente por lo

\[f^{−1}(x)≠ \dfrac{1}{f(x)}. \nonumber \]

La figura\(\PageIndex{1}\) muestra la relación entre el dominio y el rango de\(f\) y el dominio y rango de\(f^{−1}\).

Figura\(\PageIndex{1}\): Dada una función\(f\) y su inversa\(f^{−1},f^{−1}(y)=x\) si y solo si\(f(x)=y\). El rango de\(f\) se convierte en el dominio de\(f^{−1}\) y el dominio de\(f\) se convierte en el rango de\(f^{−1}\).

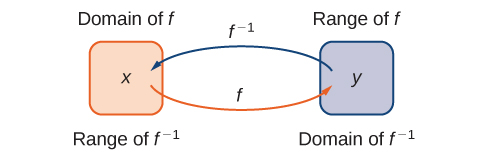
Recordemos que una función tiene exactamente una salida por cada entrada. Por lo tanto, para definir una función inversa, necesitamos mapear cada entrada a exactamente una salida. Por ejemplo, vamos a tratar de encontrar la función inversa para\(f(x)=x^2\). Resolviendo la ecuación\(y=x^2\) para\(x\), llegamos a la ecuación\(x=±\sqrt{y}\). Esta ecuación no describe\(x\) como una función de\(y\) porque hay dos soluciones a esta ecuación para cada uno\(y>0\). El problema al tratar de encontrar una función inversa para\(f(x)=x^2\) es que se envían dos entradas a la misma salida para cada salida\(y>0\). La función\(f(x)=x^3+4\) discutida anteriormente no tuvo este problema. Para esa función, cada entrada se envió a una salida diferente. Una función que envía cada entrada a una salida diferente se denomina función uno a uno.

Definición: Funciones uno a uno

Decimos que una función\(f\) es una función uno a uno si\(f(x_1)≠f(x_2)\) cuando\(x_1≠x_2\).

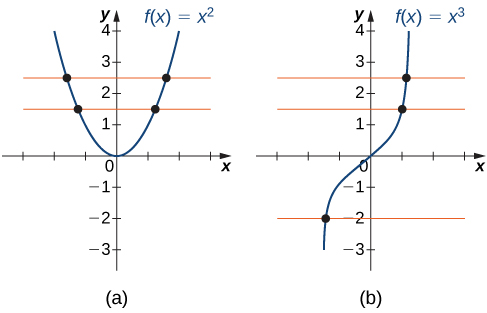
Una forma de determinar si una función es uno a uno es mirando su gráfica. Si una función es uno a uno, entonces no se pueden enviar dos entradas a la misma salida. Por lo tanto, si dibujamos una línea horizontal en cualquier parte del\(xy\) plano, de acuerdo con la prueba de línea horizontal, no puede intersectar la gráfica más de una vez. Observamos que la prueba de línea horizontal es diferente de la prueba de línea vertical. La prueba de línea vertical determina si una gráfica es la gráfica de una función. La prueba de línea horizontal determina si una función es uno a uno (Figura\(\PageIndex{2}\)).

Prueba de Línea Horizontal

Una función\(f\) es uno a uno si y solo si cada línea horizontal interseca la gráfica de\(f\) no más de una vez.

Figura\(\PageIndex{2}\): (a) La función no\(f(x)=x^2\) es uno a uno porque falla la prueba de línea horizontal. (b) La función\(f(x)=x^3\) es uno a uno porque pasa la prueba de línea horizontal.

Ejemplo\(\PageIndex{1}\): Determining Whether a Function Is One-to-One

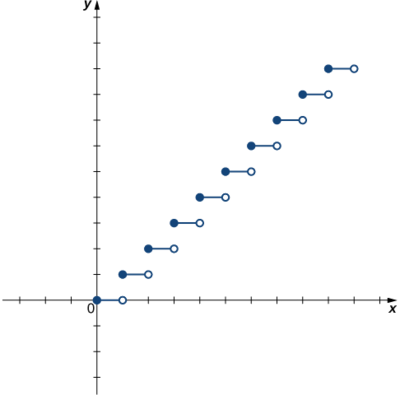
Para cada una de las siguientes funciones, utilice la prueba de línea horizontal para determinar si es uno a uno.

a)

b)

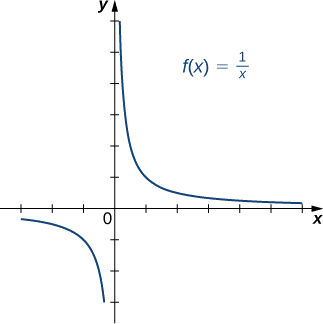
Solución

a) Dado que la línea horizontal\(y=n\) para cualquier entero\(n≥0\) cruza la gráfica más de una vez, esta función no es uno a uno.

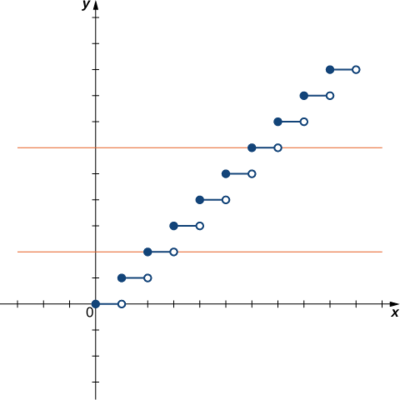
b) Dado que cada línea horizontal cruza la gráfica una vez (como máximo), esta función es de uno a uno.

Ejercicio\(\PageIndex{1}\)

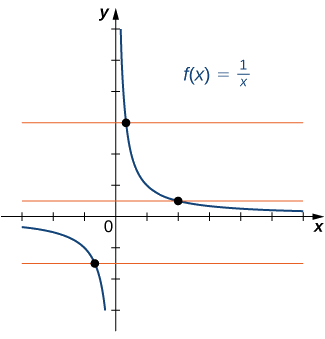
¿La función está\(f\) graficada en la siguiente imagen uno a uno?

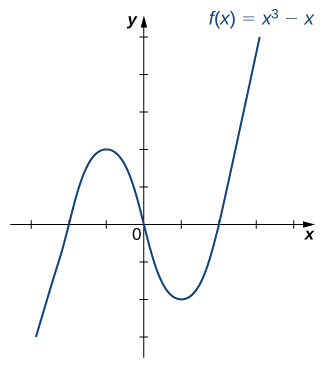
Solución

Utilice la prueba de línea horizontal.

Contestar

No

Encontrar el inverso de una función

Ahora podemos considerar funciones uno a uno y mostrar cómo encontrar sus inversos. Recordemos que una función mapea elementos en el dominio de\(f\) a elementos en el rango de\(f\). La función inversa mapea cada elemento desde el rango de\(f\) espalda a su elemento correspondiente del dominio de\(f\). Por lo tanto, para encontrar la función inversa de una función uno a uno\(f\), dada cualquiera\(y\) en el rango de\(f\), necesitamos determinar cuál\(x\) en el dominio de\(f\) satisface\(f(x)=y\). Dado que\(f\) es uno a uno, existe exactamente uno de esos valores\(x\). Podemos encontrar ese valor\(x\) resolviendo la ecuación\(f(x)=y\) para\(x\). Al hacerlo, somos capaces de escribir\(x\) en función de\(y\) donde el dominio de esta función es el rango de\(f\) y el rango de esta nueva función es el dominio de\(f\). En consecuencia, esta función es la inversa de\(f\), y escribimos\(x=f^{−1}(y)\). Como normalmente usamos la variable\(x\) para denotar la variable independiente e y para denotar la variable dependiente, a menudo intercambiamos los roles de\(x\) y\(y\), y escribimos\(y=f^{−1}(x)\). Representar la función inversa de esta manera también es útil más adelante cuando graficamos una función\(f\) y su inversa\(f^{−1}\) en los mismos ejes.

Estrategia de resolución de problemas: encontrar una función inversa

1. Resolver la ecuación\(y=f(x)\) para\(x\).
2. Intercambien las variables\(x\) y\(y\) y escriban\(y=f^{−1}(x)\).

Ejemplo\(\PageIndex{2}\): Finding an Inverse Function

Encuentra la inversa para la función\(f(x)=3x−4.\) Estado el dominio y el rango de la función inversa. Verifica que\(f^{−1}(f(x))=x.\)

Solución

Siga los pasos descritos en la estrategia.

Paso 1. Si\(y=3x−4,\) entonces\(3x=y+4\) y\(x=\frac{1}{3}y+\frac{4}{3}.\)

Paso 2. Reescribir como\(y=\frac{1}{3}x+\frac{4}{3}\) y dejar\(y=f^{−1}(x)\) .Por lo tanto,\(f^{−1}(x)=\frac{1}{3}x+\frac{4}{3}\).

Dado que el dominio de\(f\) es\((−∞,∞)\), el rango de\(f^{−1}\) es\((−∞,∞)\). Dado que el rango de\(f\) es\((−∞,∞)\), el dominio de\(f^{−1}\) es\((−∞,∞)\).

Se puede verificar\(f^{−1}(f(x))=x\) por escrito

\(f^{−1}(f(x))=f^{−1}(3x−4)=\frac{1}{3}(3x−4)+\frac{4}{3}=x−\frac{4}{3}+\frac{4}{3}=x.\)

Tenga en cuenta que\(f^{−1}(x)\) para ser la inversa de\(f(x)\), ambos\(f^{−1}(f(x))=x\) y\(f(f^{−1}(x))=x\) para todos\(x\) en el dominio de la función interior.

Ejercicio\(\PageIndex{2}\)

Encuentra la inversa de la función\(f(x)=3x/(x−2)\). Declarar el dominio y el rango de la función inversa.

Pista

Utilice la Estrategia de Resolución de Problemas para encontrar funciones inversas.

Responder

\(f^{−1}(x)=\dfrac{2x}{x−3}\). El dominio de\(f^{−1}\) es\(\{x\,|\,x≠3\}\). El rango de\(f^{−1}\) es\(\{y\,|\,y≠2\}\).

Graficar funciones inversas

Consideremos la relación entre la gráfica de una función\(f\) y la gráfica de su inversa. Considera la gráfica de que\(f\) se muestra en la Figura\(\PageIndex{3}\) y un punto\((a,b)\) en la gráfica. Desde\(b=f(a)\) entonces\(f^{−1}(b)=a\). Por lo tanto, cuando\(f^{−1}\) graficamos, el punto\((b,a)\) está en la gráfica. Como resultado, la gráfica de\(f^{−1}\) es un reflejo de la gráfica de\(f\) alrededor de la línea\(y=x\).

Figura\(\PageIndex{3}\): (a) La gráfica de esta función\(f\) muestra el punto\((a,b)\) en la gráfica de\(f\). (b) Ya que\((a,b)\) está en la gráfica de\(f\), el punto\((b,a)\) está en la gráfica de\(f^{−1}\). La gráfica de\(f^{−1}\) es un reflejo de la gráfica de\(f\) alrededor de la línea\(y=x\).

Ejemplo\(\PageIndex{3}\): Sketching Graphs of Inverse Functions

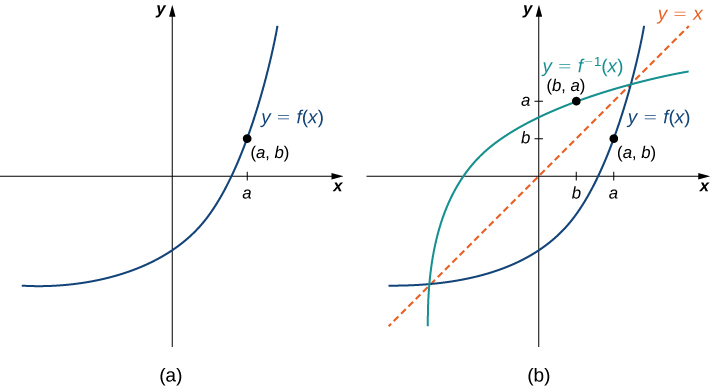
Para la gráfica de\(f\) en la siguiente imagen, bosquejar una gráfica de\(f^{−1}\) esbozando la línea\(y=x\) y usando simetría. Identificar el dominio y el rango de\(f^{−1}\).

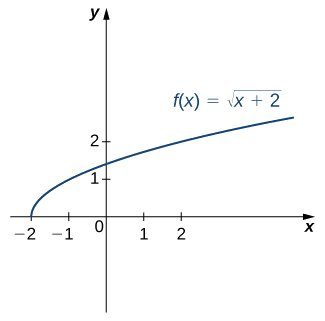
Solución

Refleja la gráfica sobre la línea\(y=x\). El dominio de\(f^{−1}\) es\([0,∞)\). El rango de\(f^{−1}\) es\([−2,∞)\). Mediante el uso de la estrategia anterior para encontrar funciones inversas, podemos verificar que la función inversa es\(f^{−1}(x)=x^2−2\), como se muestra en la gráfica.

Ejercicio\(\PageIndex{3}\)

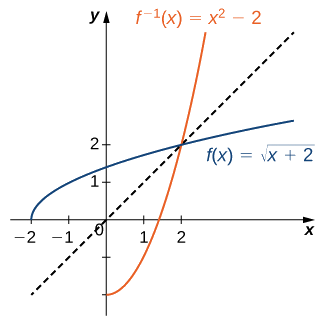
Esboce la gráfica de\(f(x)=2x+3\) y la gráfica de su inversa utilizando la propiedad de simetría de las funciones inversas.

Pista

Los gráficos son simétricos sobre la línea\(y=x\)

Contestar

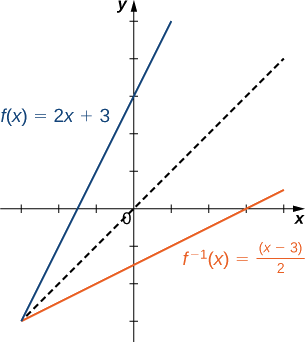
Restringir dominios

Como hemos visto,\(f(x)=x^2\) no tiene una función inversa porque no es uno-a-uno. Sin embargo, podemos elegir un subconjunto del dominio de\(f\) tal manera que la función sea uno a uno. Este subconjunto se denomina dominio restringido. Al restringir el dominio de\(f\), podemos definir una nueva función\(g\) tal que el dominio de\(g\) es el dominio restringido de\(f\) y\(g(x)=f(x)\) para todos\(x\) en el dominio de\(g\). Entonces podemos definir una función inversa para\(g\) sobre ese dominio. Por ejemplo, dado que\(f(x)=x^2\) es uno a uno en el intervalo\([0,∞)\), podemos definir una nueva función\(g\) tal que el dominio de\(g\) es\([0,∞)\) y\(g(x)=x^2\) para todos\(x\) en su dominio. Dado que\(g\) es una función uno a uno, tiene una función inversa, dada por la fórmula\(g^{−1}(x)=\sqrt{x}\). Por otro lado, la función también\(f(x)=x^2\) es uno-a-uno en el dominio\((−∞,0]\). Por lo tanto, también podríamos definir una nueva función\(h\) tal que el dominio de\(h\) es\((−∞,0]\) y\(h(x)=x^2\) para todos\(x\) en el dominio de\(h\). Entonces\(h\) es una función uno a uno y también debe tener una inversa. Su inverso viene dado por la fórmula\(h^{−1}(x)=−\sqrt{x}\) (Figura\(\PageIndex{4}\)).

Figura\(\PageIndex{4}\): (a) Para\(g(x)=x^2\) restringido a\([0,∞)\),\(g^{−1}(x)=\sqrt{x}\). b) Por\(h(x)=x^2\) restringidos a\((−∞,0]\),\(h^{−1}(x)=−\sqrt{x}\).

Ejemplo\(\PageIndex{4}\): Restricting the Domain

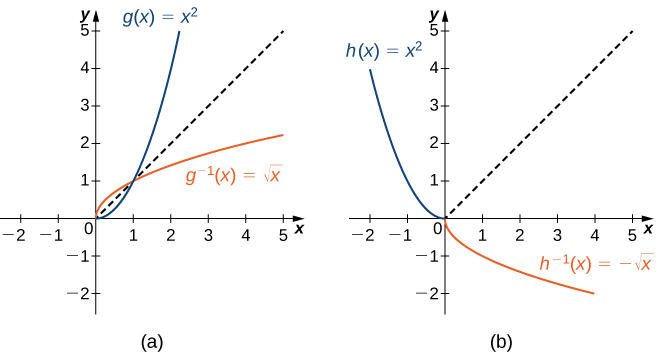
Considera la función\(f(x)=(x+1)^2\).

1. Esboce la gráfica\(f\) y use la prueba de línea horizontal para mostrar que no\(f\) es uno a uno.
2. Mostrar que\(f\) es uno a uno en el dominio restringido\([−1,∞)\). Determinar el dominio y el rango para la inversa de\(f\) en este dominio restringido y encontrar una fórmula para\(f^{−1}\).

Solución

a) La gráfica de\(f\) es la gráfica de\(1\) unidad\(y=x^2\) desplazada a la izquierda. Dado que existe una línea horizontal que cruza la gráfica más de una vez, no\(f\) es uno a uno.

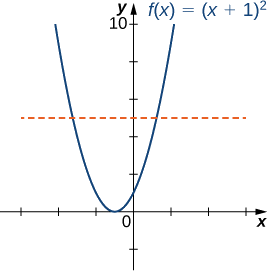
b) En el intervalo\([−1,∞),\;f\) es uno a uno.

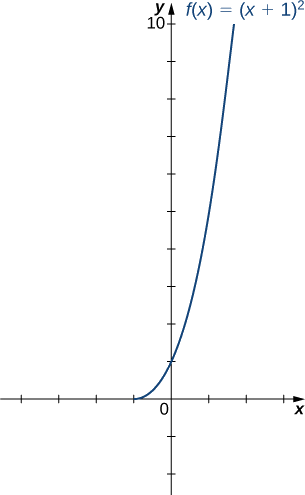
El dominio y el rango de\(f^{−1}\) están dados por el rango y el dominio de\(f\), respectivamente. Por lo tanto, el dominio de\(f^{−1}\) es\([0,∞)\) y el rango de\(f^{−1}\) es\([−1,∞)\). Para encontrar una fórmula para\(f^{−1}\), resuelve la ecuación\(y=(x+1)^2\) para\(x.\) Si\(y=(x+1)^2\), entonces\(x=−1±\sqrt{y}\). Ya que estamos restringiendo el dominio al intervalo donde\(x≥−1\), necesitamos\(±\sqrt{y}≥0\). Por lo tanto,\(x=−1+\sqrt{y}\). Intercambiando\(x\) y\(y\), escribimos\(y=−1+\sqrt{x}\) y concluimos eso\(f^{−1}(x)=−1+\sqrt{x}\).

Ejercicio\(\PageIndex{4}\)

Considera\(f(x)=1/x^2\) restringido al dominio\((−∞,0)\). Verifique que\(f\) sea uno a uno en este dominio. Determinar el dominio y rango de la inversa de\(f\) y encontrar una fórmula para\(f^{−1}\).

Pista

El dominio y rango de\(f^{−1}\) viene dado por el rango y dominio de\(f\), respectivamente. Para encontrar\(f^{−1}\), resolver\(y=1/x^2\) para\(x\).

Contestar

El dominio de\(f^{−1}\) es\((0,∞)\). El rango de\(f^{−1}\) es\((−∞,0)\). La función inversa viene dada por la fórmula\(f^{−1}(x)=−1/\sqrt{x}\).

Funciones trigonométricas inversas

Las seis funciones trigonométricas básicas son periódicas y, por lo tanto, no son una a una. Sin embargo, si restringimos el dominio de una función trigonométrica a un intervalo en el que es uno a uno, podemos definir su inversa. Considera la función sinusoidal. La función seno es uno a uno en un número infinito de intervalos, pero la convención estándar es restringir el dominio al intervalo\(\left[−\frac{π}{2},\frac{π}{2}\right]\). Al hacerlo, definimos la función sinusoidal inversa en el dominio de\([−1,1]\) tal manera que para cualquiera\(x\) en el intervalo\([−1,1]\), la función sinusoidal inversa nos dice qué ángulo\(θ\) en el intervalo\(\left[−\frac{π}{2},\frac{π}{2}\right]\) satisface\(\sin θ=x\). De igual manera, podemos restringir los dominios de las otras funciones trigonométricas para definir funciones trigonométricas inversas, que son funciones que nos indican qué ángulo en un cierto intervalo tiene un valor trigonométrico especificado.

Definición: funciones trigonométricas inversas

La función sinusoidal inversa, denotada\(\sin^{−1}\) o\(\arcsin\), y la función coseno inversa, denotada\(\cos^{−1}\) o\(\arccos\), se definen en el dominio de la\(D=\{x|−1≤x≤1\}\) siguiente manera:

\(\sin^{−1}(x)=y\)

• si y sólo si\(\sin(y)=x\) y\(−\frac{π}{2}≤y≤\frac{π}{2}\);

\(\cos^{−1}(x)=y\)

• si y sólo si\(\cos(y)=x\) y\(0≤y≤π\).

La función tangente inversa, denotada\(\tan^{−1}\) o\(\arctan\), y la función cotangente inversa, denotada\(\cot^{−1}\) o\(\operatorname{arccot}\), se definen en el dominio de la\(D=\{x|−∞<x<∞\}\) siguiente manera:

\(\tan^{−1}(x)=y\)

• si y sólo si\(\tan(y)=x\) y\(−\frac{π}{2}<y<\frac{π}{2}\);

\(\cot^{−1}(x)=y\)

• si y sólo si\(\cot(y)=x\) y\(0<y<π\).

La función cosecante inversa, denotada\(\csc^{−1}\) o\(\operatorname{arccsc}\), y la función secante inversa, denotada\(\sec^{−1}\) o\(\operatorname{arcsec}\), se definen en el dominio de la\(D=\{x\,|\,|x|≥1\}\) siguiente manera:

\(\csc^{−1}(x)=y\)

• si y sólo si\(\csc(y)=x\) y\(−\frac{π}{2}≤y≤\frac{π}{2}, \, y≠0\);

\(\sec^{−1}(x)=y\)

• si y sólo si\(\sec(y)=x\) y\(0≤y≤π, \, y≠π/2\).

Para graficar las funciones trigonométricas inversas, utilizamos las gráficas de las funciones trigonométricas restringidas a los dominios definidos anteriormente y reflejamos las gráficas sobre la línea\(y=x\) (Figura\(\PageIndex{5}\)).

Figura\(\PageIndex{5}\): La gráfica de cada una de las funciones trigonométricas inversas es una reflexión sobre la línea\(y=x\) de la función trigonométrica restringida correspondiente.

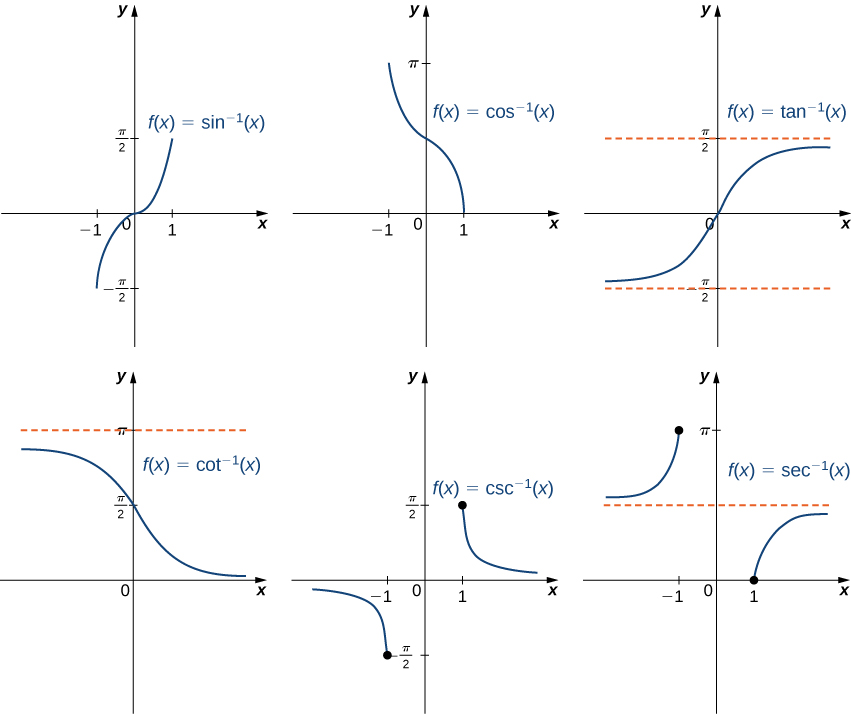
Al evaluar una función trigonométrica inversa, la salida es un ángulo. Por ejemplo, para evaluar\(\cos^{−1}\left(\frac{1}{2}\right)\), necesitamos encontrar un ángulo\(θ\) tal que\(\cos θ=\frac{1}{2}\). Claramente, muchos ángulos tienen esta propiedad. No obstante, dada la definición de\(\cos^{−1}\), necesitamos el ángulo\(θ\) que no sólo resuelva esta ecuación, sino que también se encuentra en el intervalo\([0,π]\). Concluimos que\(\cos^{−1}\left(\frac{1}{2}\right)=\frac{π}{3}\).

Consideramos ahora una composición de una función trigonométrica y su inversa. Por ejemplo, considere las dos expresiones\(\sin\left(\sin^{−1}\left(\frac{\sqrt{2}}{2}\right)\right)\) y\(\sin^{−1}(\sin(π)).\)

Para el primero, simplificamos de la siguiente manera:

\[\sin\left(\sin^{−1}\left(\frac{\sqrt{2}}{2}\right)\right)=\sin\left(\frac{π}{4}\right)=\frac{\sqrt{2}}{2}.\nonumber \]

Para el segundo, tenemos

\[\sin^{−1}(\sin(π))=\sin^{−1}(0)=0.\nonumber \]

Se supone que la función inversa “deshace” la función original, así que ¿por qué no\(\sin^{−1}(\sin(π))=π?\) Recordando nuestra definición de funciones inversas, una función\(f\) y su inversa\(f^{−1}\) satisfacen las condiciones\(f(f^{−1}(y))=y\) para todos\(y\) en el dominio de\(f^{−1}\) y\(f^{−1}(f(x))=x\) para todos\(x\) en el dominio de\(f\), entonces, ¿qué pasó aquí? El problema es que la función sinusoidal inversa,\(\sin^{−1}\), es la inversa de la función sinusoidal restringida definida en el dominio\(\left[−\frac{π}{2},\frac{π}{2}\right]\). Por lo tanto, pues\(x\) en el intervalo\([−\frac{π}{2},\frac{π}{2}]\), es cierto que\(\sin^{−1}(\sin x)=x\). Sin embargo, para valores\(x\) fuera de este intervalo, la ecuación no se mantiene, aunque\(\sin^{−1}(\sin x)\) esté definida para todos los números reales\(x\).

¿Y eso\(\sin(\sin^{−1}y)?\) tiene un problema similar? La respuesta es no. Dado que el dominio de\(\sin^{−1}\) es el intervalo\([−1,1]\), concluimos que\(\sin\left(\sin^{−1}y\right)=y\) si\(−1≤y≤1\) y la expresión no está definida para otros valores de\(y\). Para resumir,

\(\sin(\sin^{−1}y)=y\)si\(−1≤y≤1\)

y

\(\sin^{−1}(\sin x)=x\)si\(−\frac{π}{2}≤x≤\frac{π}{2}.\)

Del mismo modo, para la función coseno,

\(\cos(\cos^{−1}y)=y\)si\(−1≤y≤1\)

y

\(\cos^{−1}(\cos x)=x\)si\(0≤x≤π.\)

Propiedades similares se mantienen para las otras f unciones trigonométricas y sus inversos.

Ejemplo\(\PageIndex{5}\): Evaluating Expressions Involving Inverse Trigonometric Functions

Evalúe cada una de las siguientes expresiones.

1. \(\sin^{−1}\left(−\frac{\sqrt{3}}{2}\right)\)
2. \(\tan\left(\tan^{−1}\left(−\frac{1}{\sqrt{3}}\right)\right)\)
3. \(\cos^{−1}\left(\cos\left(\frac{5π}{4}\right)\right)\)
4. \(\sin^{−1}\left(\cos\left(\frac{2π}{3}\right)\right)\)

Solución

1. Evaluar\(\sin^{−1}(−\sqrt{3}/2)\) equivale a encontrar el ángulo\(θ\) tal que\(\sin θ=−\sqrt{3}/2\) y\(−π/2≤θ≤π/2\). El ángulo\(θ=−π/3\) satisface estas dos condiciones. Por lo tanto,\(\sin^{−1}(−\sqrt{3}/2)=−π/3\).
2. Primero usamos el hecho de que\(\tan^{−1}(−1/\sqrt{3})=−π/6.\) Entonces\(\tan(-π/6)=−1/\sqrt{3}\). Por lo tanto,\(\tan(\tan^{−1}(−1/\sqrt{3}))=−1/\sqrt{3}\).
3. Para evaluar\(\cos^{−1}(\cos(5π/4))\), primero use el hecho de que\(\cos(5π/4)=−\sqrt{2}/2\). Entonces necesitamos encontrar el ángulo\(θ\) tal que\(\cos(θ)=−\sqrt{2}/2\) y\(0≤θ≤π\). Ya que\(3π/4\) satisface ambas condiciones, tenemos\(\cos^{-1}(\cos(5π/4))=\cos^{−1}(−\sqrt{2}/2))=3π/4\).
4. Ya que\(\cos(2π/3)=−1/2\), necesitamos evaluar\(\sin^{−1}(−1/2)\). Es decir, necesitamos encontrar el ángulo\(θ\) tal que\(\sin(θ)=−1/2\) y\(−π/2≤θ≤π/2\). Dado que\(−π/6\) satisface ambas condiciones, podemos concluir que\(\sin^{−1}(\cos(2π/3))=\sin^{−1}(−1/2)=−π/6.\)

El valor máximo de una función

En muchas áreas de la ciencia, la ingeniería y las matemáticas, es útil conocer el valor máximo que puede obtener una función, aunque no sepamos su valor exacto en un instante dado. Por ejemplo, si tenemos una función que describa la resistencia de una viga de techo, querríamos saber el peso máximo que la viga puede soportar sin romperse. Si tenemos una función que describa la velocidad de un tren, querríamos saber su velocidad máxima antes de que salte de los rieles. El diseño seguro a menudo depende de conocer los valores máximos.

Este proyecto describe un ejemplo sencillo de una función con un valor máximo que depende de dos coeficientes de ecuación. Veremos que los valores máximos pueden depender de varios factores distintos de la variable independiente\(x\).

1. Considera la gráfica en Figura\(\PageIndex{6}\) de la función\(y=\sin x+\cos x.\) Describir su forma general. ¿Es periódico? ¿Cómo lo sabes?

Figura\(\PageIndex{6}\): La gráfica de\(y=\sin x+\cos x\).

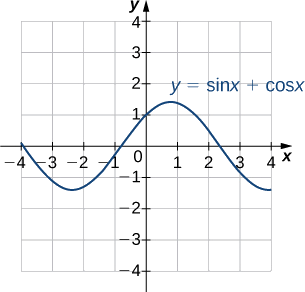
Usando una calculadora gráfica u otro dispositivo gráfico, estime los\(y\) valores\(x\) - y -del punto máximo para la gráfica (el primer punto de ese tipo donde\(x > 0\)). Puede ser útil expresar el\(x\) valor -como un múltiplo de\(π.\)

2. Ahora considere otras gráficas de la forma\(y=A\sin x+B\cos x\) para diversos valores de\(A\) y\(B.\) Esbozar la gráfica cuándo\(A = 2\)\(B = 1,\) y y encuentre los\(y\) valores\(x\) - y -para el punto máximo. (Recuerde expresar el\(x\) -valor como un múltiplo de\(π\), si es posible.) ¿Se ha movido?

3. Repita para ¿\(A = 1, \,B = 2.\)Hay alguna relación con lo que encontraste en la parte (2)?

4. Complete la siguiente tabla, agregando algunas opciones propias para\(A\) y\(B:\)

\(A\)	\(B\)	\(x\)	\(y\)	\(A\)	\(B\)	\(x\)	\(y\)
\ (A\)” style="vertical-align:middle; ">0	\ (B\)” style="vertical-align:middle; ">1	\ (x\)” style="vertical-align:middle; ">	\ (y\)” style="vertical-align:middle; ">	\ (A\)” style="vertical-align:middle; ">3	\ (B\)” style="vertical-align:middle; ">4	\ (x\)” style="vertical-align:middle; ">	\ (y\)” style="vertical-align:middle; ">
\ (A\)” style="vertical-align:middle; ">1	\ (B\)” style="vertical-align:middle; ">0	\ (x\)” style="vertical-align:middle; ">	\ (y\)” style="vertical-align:middle; ">	\ (A\)” style="vertical-align:middle; ">4	\ (B\)” style="vertical-align:middle; ">3	\ (x\)” style="vertical-align:middle; ">	\ (y\)” style="vertical-align:middle; ">
\ (A\)” style="vertical-align:middle; ">1	\ (B\)” style="vertical-align:middle; ">1	\ (x\)” style="vertical-align:middle; ">	\ (y\)” style="vertical-align:middle; ">	\ (A\)” style="vertical-align:middle; ">\(\sqrt{3}\)	\ (B\)” style="vertical-align:middle; ">1	\ (x\)” style="vertical-align:middle; ">	\ (y\)” style="vertical-align:middle; ">
\ (A\)” style="vertical-align:middle; ">1	\ (B\)” style="vertical-align:middle; ">2	\ (x\)” style="vertical-align:middle; ">	\ (y\)” style="vertical-align:middle; ">	\ (A\)” style="vertical-align:middle; ">1	\ (B\)” style="vertical-align:middle; ">\(\sqrt{3}\)	\ (x\)” style="vertical-align:middle; ">	\ (y\)” style="vertical-align:middle; ">
\ (A\)” style="vertical-align:middle; ">2	\ (B\)” style="vertical-align:middle; ">1	\ (x\)” style="vertical-align:middle; ">	\ (y\)” style="vertical-align:middle; ">	\ (A\)” style="vertical-align:middle; ">12	\ (B\)” style="vertical-align:middle; ">5	\ (x\)” style="vertical-align:middle; ">	\ (y\)” style="vertical-align:middle; ">
\ (A\)” style="vertical-align:middle; ">2	\ (B\)” style="vertical-align:middle; ">2	\ (x\)” style="vertical-align:middle; ">	\ (y\)” style="vertical-align:middle; ">	\ (A\)” style="vertical-align:middle; ">5	\ (B\)” style="vertical-align:middle; ">12	\ (x\)” style="vertical-align:middle; ">	\ (y\)” style="vertical-align:middle; ">

5. Trate de averiguar la fórmula para los\(y\) -valores.

6. La fórmula para los\(x\) -valores es un poco más difícil. Los puntos más útiles de la tabla son\((1,1),\, (1,\sqrt{3}),\, (\sqrt{3},1).\) (Pista: Considere las funciones trigonométricas inversas.)

7. Si encontró fórmulas para las piezas (5) y (6), demuestre que funcionan juntas. Es decir, sustituya la fórmula\(x\) -value que encontraste\(y=A\sin x+B\cos x\) y simplifícala para llegar a la fórmula\(y\) -value que encontraste.

Conceptos clave

• Para que una función tenga una inversa, la función debe ser uno a uno. Dada la gráfica de una función, podemos determinar si la función es uno a uno usando la prueba de línea horizontal.
• Si una función no es uno a uno, podemos restringir el dominio a un dominio más pequeño donde la función es uno a uno y luego definir la inversa de la función en el dominio más pequeño.
• Para una función\(f\) y su inverso\(f^{−1},\, f(f^{−1}(x))=x\) para todos\(x\) en el dominio de\(f^{−1}\) y\(f^{−1}(f(x))=x\) para todos\(x\) en el dominio de\(f\).
• Dado que las funciones trigonométricas son periódicas, necesitamos restringir sus dominios para definir las funciones trigonométricas inversas.
• La gráfica de una función\(f\) y su inversa\(f^{−1}\) son simétricas sobre la línea\(y=x.\)

Ecuaciones Clave

• Función inversa

\(f^{−1}(f(x))=x\)para todos\(x\) en\(D,\) y\(f(f^{−1}(y))=y\) para todos\(y\) en\(R\).

Glosario

prueba de línea horizontal

una función\(f\) es uno a uno si y solo si cada línea horizontal interseca la gráfica de\(f\), como máximo, una vez

función inversa

para una función\(f\), la función inversa\(f^{−1}\) satisface\(f^{−1}(y)=x\) si\(f(x)=y\)

funciones trigonométricas inversas

las inversas de las funciones trigonométricas se definen en dominios restringidos donde son funciones uno a uno

función uno a uno

una función\(f\) es uno a uno si\(f(x_1)≠f(x_2)\) si\(x_1≠x_2\)

dominio restringido

un subconjunto del dominio de una función\(f\)