8.3: Ecuaciones Diofantinas Lineales

Última actualización
Guardar como PDF

Page ID: 116082

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Vista previa de la actividad$\PageIndex{1}$: Integer Solutions for Linear Equations in One Variable

¿La ecuación lineal$6x = 42$ tiene una solución que es un entero? Explique.
¿La ecuación lineal$7x = -21$ tiene una solución que es un entero? Explique.
¿La ecuación lineal$4x = 9$ tiene una solución que es un entero? Explique.
¿La ecuación lineal$-3x = 20$ tiene una solución que es un entero? Explique.
Demostrar el siguiente teorema:

Teorema 8.18

Déjalo$a, b \in \mathbb{Z}$ con$a \ne 0$.

Si$a$ divide$b$, entonces la ecuación$ax = b$ tiene exactamente una solución que es un entero.
Si$a$ no divide$b$, entonces la ecuación no$ax = b$ tiene solución que sea un entero.

Vista previa de la actividad$\PageIndex{2}$: Linear Equations in Two Variables

Encontrar enteros$x$ y$y$ así eso$2x + 6y = 25$ o explicar por qué no es posible encontrar tal par de enteros.
Encontrar enteros$x$ y$y$ así eso$6x - 9y = 100$ o explicar por qué no es posible encontrar tal par de enteros.
Observe que$x = 2$ y$y = 1$ es una solución de la ecuación$3x + 5y = 11$, y eso$x = 7$ y también$y = -2$ es una solución de la ecuación$3x + 5y = 11$.

(a) Encontrar dos pares de enteros$x$ y$y$ para que$x > 7$ y$3x + 5y = 11$. (Trate de mantener los valores enteros de x lo más pequeños posible.)
(b) Encontrar dos pares de enteros$x$ y$y$ para que$x < 2$ y$3x + 5y = 11$. (Trate de mantener los valores enteros de$x$ lo más cerca posible de 2.)
(c) Determinar fórmulas (una para x y otra para y) que generarán pares de enteros$x$ y$y$ para que$3x + 5y = 11$.
Pista: Las dos fórmulas se pueden escribir en la forma$x = 2 + km$ y$y = 1 + kn$, donde$k$ es un entero arbitrario$m$ y y$n$ son enteros específicos.

Observe que$x = 4$ y$y = 0$ es una solución de la ecuación$4x + 6y = 16$, y eso$x = 7$ y$y = -2$ es una solución de la ecuación$4x + 6y = 16$. (a) Encontrar dos pares de enteros$x$ y$y$ para que$x > 7$ y$4x + 6y = 16$. (Trate de mantener los valores enteros de$x$ lo más pequeños posible.)
(b) Encontrar dos pares de enteros$x$ y$y$ para que$x < 4$ y$4x + 6y = 16$. (Trate de mantener los valores enteros$x$ lo más cercanos a 4 como sea posible.)
(c) Determinar fórmulas (uno para$x$ y uno para$y$) que generarán pares de enteros x e y para que$4x + 6y = 16$.
Pista: Las dos fórmulas se pueden escribir en la forma$x = 4 + km$ y$y = 0 + kn$, donde$k$ es un entero arbitrario$m$ y y$n$ son enteros específicos.

En las dos actividades de vista previa, solo nos interesaron soluciones enteras para ciertas ecuaciones. En tales casos, le damos un nombre especial a la ecuación.

Definición: Ecuación diofantina

Una ecuación cuyas soluciones se requieren para ser números enteros se denomina ecuación diofantina.

Las ecuaciones diofantinas se nombran en honor del matemático griego Diofanto de Alejandría (circa 300 c.e.). Se sabe muy poco sobre la vida de Diofanto excepto que probablemente vivió en Alejandría a principios del siglo IVc.e. y probablemente fue el primero en usar letras para cantidades desconocidas en problemas aritméticos. Su obra más famosa, Arithmetica, consta de aproximadamente 130 problemas y sus soluciones. La mayoría de estos problemas involucraron soluciones de ecuaciones en varios números de variables. Es interesante señalar que Diofantus no restringió sus soluciones a los enteros sino que reconoció soluciones numéricas racionales también. Hoy, sin embargo, las soluciones para una llamada ecuación diofantina deben ser números enteros.

Definición: ecuación diofantina lineal en una variable

Si$a$ y$b$ son enteros con$a \ne 0$, entonces la ecuación$ax = b$ es una ecuación Diofantina lineal en una variable.

Teorema 8.18 en Preview Actividad nos$\PageIndex{1}$ proporciona resultados que nos permiten determinar qué ecuaciones diofantinas lineales en una variable tienen soluciones y cuáles no tienen solución.

Una ecuación lineal de Diofantina en dos variables se puede definir de manera similar a la definición de una ecuación de Diofantina lineal en una variable.

Definición: ecuación diofantina lineal en dos variables

Dejar$a$,$b$, y$c$ ser enteros con$a \ne 0$ y$b \ne 0$. La ecuación de Diofantina$ax + by = c$ se denomina ecuación Diofantina lineal en dos variables.

Las ecuaciones que se investigaron en Preview Activity$\PageIndex{2}$ fueron ecuaciones lineales Diofantinas en dos variables. El problema de determinar todas las soluciones de una ecuación lineal de Diofantina ha sido completamente resuelto. Antes de exponer el resultado general, proporcionaremos algunos ejemplos más.

Ejemplo 8.19: Una Ecuación Diofantina Lineal en Dos Variables

El siguiente ejemplo es similar a los ejemplos estudiados en Preview Activity$\PageIndex{2}$.

Podemos usar la sustitución para verificar eso$x = 2$ y$y = -1$ es una solución de la ecuación lineal de Diofantina

$4x + 3y = 5$.

En la siguiente tabla se muestran otras soluciones de esta ecuación de Diofantina.

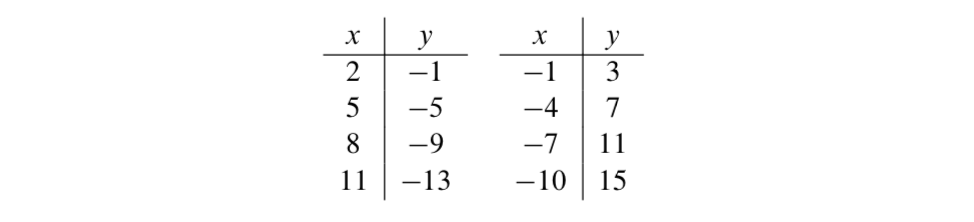
$2019-04-16 10.33.03.png$

Sería bueno determinar el patrón que exhiben estas soluciones. Si consideramos la solución$x = 2$ y$y = -1$ que es el “punto de partida”, entonces podemos ver que las otras soluciones se obtienen sumando 3$x$ y restando 4 de$y$ en la solución anterior. Así podemos escribir estas soluciones a la ecuación como

$x = 2 + 3k$y$y = -1 - 4k$,

donde$k$ es un número entero. Podemos usar sustitución y álgebra para verificar que estas expresiones para$x$ y$y$ dar soluciones de esta ecuación de la siguiente manera:

\[\begin{array} {rcl} {4x + 3y} &= & {4(2 + 3k) + 3(-1 - 4k)} \\ {} &= & {(8 + 12k) + (-3 - 12k)} \\ {} &= & {5.} \end{array}\]

Debemos señalar que aún no hemos probado que estas soluciones sean todas de las soluciones de la ecuación Diofantina$4x + 3y = 5$. Esto se hará más adelante.

Si la forma general para una ecuación Diofantina lineal es$ax + by = c$, entonces para este ejemplo,$a = 4$ y$b = 3$. Observe que para esta ecuación, comenzamos con una solución y obtuvimos otras soluciones sumando$b = 3$$x$ y restando$a = 4$$y$ en la solución anterior. Además, observe que gcd (3, 4) = 1.

Comprobación de Progreso 8.20: Un Ejemplo de una Ecuación Diofantina Lineal

Verifique que en la siguiente tabla se muestren algunas soluciones de la ecuación lineal de Diofantina$6x + 9y = 12$.
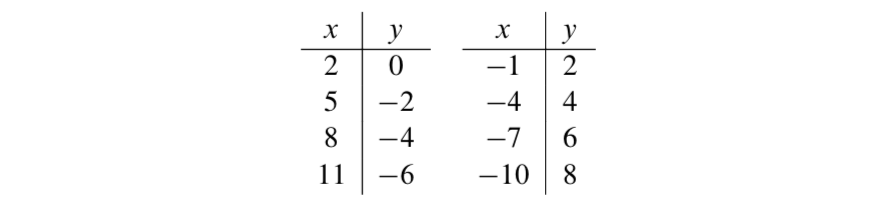
$2019-04-16 10.38.40.png$
Siga el patrón en esta tabla para determinar fórmulas para$x$ y$y$ que generarán soluciones enteras de la ecuación$6x + 9y = 12$. Verificar que las fórmulas realmente produzcan soluciones para la ecuación$6x + 9y = 12$.

Contestar: Agrega textos aquí. No borre primero este texto.

Comprobación de progreso 8.21: Revisitando la actividad de vista previa$\PageIndex{2}$

¿Las soluciones para las ecuaciones lineales Diofantinas en Actividad Previa$\PageIndex{2}$ muestran el mismo tipo de patrón que las soluciones para las ecuaciones lineales de Diofantinas en el Ejemplo 8.19 y Comprobación de Progreso 8.20? Explique.

Contestar: Agrega textos aquí. No borre primero este texto.

Las soluciones para las ecuaciones lineales Diofantinas en Actividad Previa$\PageIndex{2}$, Ejemplo 8.19, y Comprobación de Progreso 8.20 proporcionan ejemplos para la segunda parte del Teorema 8.22.

Teorema 8.22

Dejar$a$,$b$ y$c$ ser enteros con$a \ne 0$ y$b \ne 0$, y dejar$d = \text{gcd}(a, b)$.

Si$d$ no divide$c$, entonces la ecuación lineal de Diofantina no$ax + by = c$ tiene solución.
Si se$d$ divide$c$, entonces la ecuación lineal de Diofantina$ax + by = c$ tiene infinitamente muchas soluciones. Además, si ($x_0$,$y_0$) es una solución particular de esta ecuación, entonces todas las soluciones de esta ecuación pueden escribirse en la forma
\[x = x_0 + \dfrac{b}{d} k\ \ \ \ \ \ \ \ \text{and}\ \ \ \ \ \ \ \ y = y_0 - \dfrac{a}{d} k,\]
para algún entero$k$.

Prueba

El comprobante de la Parte (1) es Ejercicio (1). Para la Parte (2), dejamos$a$,$b$, y$c$ ser enteros con$a \ne 0$ y$b \ne 0$, y dejamos$d = \text{gcd}(a, b)$. Eso también lo asumimos$d\ |\ c$. Ya que$d = \text{gcd}(a, b)$, Teorema 8.8 nos dice que$d$ es una combinación lineal de$a$ y$b$. Entonces existen enteros$s$ y$t$ tal que

\[d = as + bt.\]

Ya que$d\ |\ c$, existe un entero$m$ tal que$c = dm$. Ahora podemos multiplicar ambos lados de la ecuación (8.3.3) por m y obtener

\[\begin{array} {rcl} {dm} &= & {(as + bt)m} \\ {c} &= & {a(sm) + b(tm).} \end{array}\]

Esto quiere decir que$x = sm$,$y = tm$ es una solución de$ax + by = c$, y hemos demostrado que la ecuación de Diofantina$ax + by = c$ tiene al menos una solución.

Ahora vamos a$x = x_0, y = y_0$ ser cualquier solución particular de$ax + by = c$, dejar$k \in \mathbb{Z}$, y dejar

\[x = x_0 + \dfrac{b}{d} k\ \ \ \ \ \ \ \ y = y_0 - \dfrac{a}{d} k.\]

Ahora verificamos que para cada una$k \in \mathbb{Z}$, las ecuaciones en (8.3.4) producen una solución de$ax + by = c$.

\[\begin{array} {rcl} {ax + by} &= & {a(x_0 + \dfrac{b}{d} k) + b(y_0 - \dfrac{a}{d} k)} \\ {} &= & {ax_0 + \dfrac{ab}{d} k + by_0 - \dfrac{ab}{d} k} \\ {} &= & {ax_0 + by_0} \\ {} &= & {c.} \end{array}\]

Esto demuestra que la ecuación Diofantina$ax + by = c$ tiene infinitamente muchas soluciones.

Ahora mostramos que cada solución de esta ecuación puede escribirse en la forma descrita en (8.3.4). Entonces supongamos que$x$ y$y$ son enteros tales que$ax + by = c$. Entonces

$(ax + by) - (ax_0 + by_0) = c - c = 0,$

y esta ecuación se puede reescribir de la siguiente forma:

\[a(x - x_0) = b(y_0 - y).\]

Dividiendo ambos lados de esta ecuación por$d$, obtenemos

$(\dfrac{a}{d}) (x - x_0) = (\dfrac{b}{d}) (y_0 - y).$

Esto implica que

$\dfrac{a}{d}$divide$(\dfrac{b}{d}) (y_0 - y).$

Sin embargo, por el Ejercicio (7) en la Sección 8.2$text{gcd}(\dfrac{a}{d}, \dfrac{b}{d}) = 1$,, y así por el Teorema 8.12, podemos concluir que$\dfrac{a}{d}$ divide$y_0 - y$. Esto significa que existe un entero$k$ tal que$y_0 - y = \dfrac{a}{d} k$, y resolviendo para$y$ da

$y = y_0 - \dfrac{a}{d} k.$

Sustituyendo este valor por$y$ en la ecuación (8.3.5) y resolviendo$x$ rendimientos

$x = x_0 + \dfrac{b}{d}) k.$

Esto demuestra que cada solución de la ecuación Diofantina$ax + by = c$ puede escribirse en la forma prescrita en (8.3.4).

La prueba del siguiente corolario al Teorema 8.22 es Ejercicio (2)

Teorema$\PageIndex{1}$

Let$a$$b$,, y$c$ ser enteros con$a \ne 0$ y$b \ne 0$ .If$a$ y$b$ son relativamente primos, entonces la ecuación Diofantina lineal$ax + by = c$ tiene infinitamente muchas soluciones. Además, si$x_0$,$y_0$ es una solución particular de esta ecuación, entonces todas las soluciones de la ecuación están dadas por

$x = x_0 + bk$$y = y_0 - ak$

donde$k \in \mathbb{Z}$

Comprobación de Progreso 8.24 (Ecuaciones Diofantinas Lineales)

Utilice el Algoritmo Euclidiana para verificar que gcd.63; 336/ D 21. ¿Qué conclusión se puede hacer sobre la ecuación lineal de Diofantinas$63x + 336y = 40$ usando el Teorema 8.22? Si esta ecuación diofantina tiene soluciones, escriba fórmulas que generen las soluciones.
Utilice el Algoritmo Euclidiana para verificar que gcd.144; 225/ D 9. ¿Qué conclusión se puede hacer sobre la ecuación lineal de Diofantinas$144x + 225y = 27$ usando el Teorema 8.22? Si esta ecuación diofantina tiene soluciones, escriba fórmulas que generen las soluciones.

Contestar: Agrega textos aquí. No borre primero este texto.

Ejercicios 8.3

Probar Parte (1) del Teorema 8.22:
Dejar$a$,$b$, y$c$ ser enteros con$a \ne 0$ y$b \ne 0$, y let$d = \text{gcd}(a, b)$. Si$d$ no divide$c$, entonces la ecuación lineal de Diofantina no$ax + by = c$ tiene solución.
Demostrar Corolario 8.23.
Dejar$a$,$b$, y$c$ ser enteros con$a \ne 0$ y$b \ne 0$. Si$a$ y$b$ son relativamente primos, entonces la ecuación lineal de Diofantina$ax + by = c$ tiene infinitamente muchas soluciones. Además, si ($x_0, y_0$) es una solución particular de esta ecuación, entonces todas las soluciones de la ecuación están dadas por
\[x = x_0 + bk\ \ \ \ \ \ \ y = y_0 - ak,\]
dónde$k \in \mathbb{Z}$.
Determinar todas las soluciones de las siguientes ecuaciones lineales Diofantinas.

a)$9x + 14y = 1$
b)$18x + 22y = 4$
c$48x - 18y = 15$
) d$12x + 9y = 6$
) e$200x + 49y = 10$
) f$200x + 54y = 21$
) g$10x - 7y = 31$
) h)$12x + 18y = 6$
Se supone que cierto artefacto raro pesa exactamente 25 gramos. Supongamos que tiene una balanza precisa y 500 pesos cada uno de 27 gramos y pesos de 50 gramos. Explicar cómo usar el Teorema 8.22 para idear un plan para verificar el peso de este artefacto.
Pista: Observe que gcd (50, 27) = 1. Comienza escribiendo 1 como una combinación lineal de 50 y 27.
En la noche de cierto banquete, un servicio de catering ofreció la opción de dos cenas, una cena de bistec por 25 dólares y una cena vegetariana por 16 dólares. Al final de la noche, el servicio de catering presentó al anfitrión una factura (antes de impuestos y propinas) por $1461. ¿Cuál es el número mínimo de personas que podrían haber asistido al banquete? ¿Cuál es el número máximo de personas que pudieron haber asistido al banquete?
El objetivo de este ejercicio es determinar todas las soluciones (enteras) de la ecuación lineal de Diofantina en tres variables$12x_1 + 9x_2 + 16x_3 = 20.$

(a) Primero, observe que gcd (12, 9) = 3. Determinar fórmulas que generarán todas las soluciones para la ecuación lineal de Diofantina$3y + 16x_3 = 20$.
(b) Explicar por qué las soluciones (para$x_1$ y$x_2$) de la ecuación Diofantina$12x_1 + 9x_2 = 3y$ pueden utilizarse para genear soluciones para$12x_1 + 9x_2 + 16x_3 = 20$.
(c) Utilizar el valor general para y del Ejercicio (6a) para determinar las soluciones de$12x_1 + 9x_2 = 3y$
(d) Utilizar los resultados de los Ejercicios (6a) y (6c) para determinar fórmulas que generarán todas las soluciones para la ecuación Diofantina$12x_1 + 9x_2 + 16x_3 = 20$.
Nota: Estas fórmulas implicarán dos parámetros enteros arbitrarios. Sustituya valores específicos por estos enteros y luego verifique la solución resultante en la ecuación original. Repita esto al menos tres veces.
(e) Verificar la solución general para$12x_1 + 9x_2 + 16x_3 = 20$ del Ejercicio (6d).
Utilice el método sugerido en el Ejercicio (6) para determinar fórmulas que generarán todas las soluciones de la ecuación Diofantina$8x_1 + 4x_2 - 6x_3 = 6$. Consulta la solución general.
Explique por qué la ecuación Diofantina no$24x_1 - 18x_2 + 60x_3 = 21$ tiene solución.
El propósito de este ejercicio será demostrar que la ecuación diofantina no lineal no$3x^2 - y^2 = -2$ tiene solución.

(a) Explique por qué si hay una solución de la ecuación Diofantina$3x^2 - y^2 = -2$, entonces esa solución también debe ser una solución de la congruencia$3x^2 - y^2 \equiv -2$ (mod 3).
(b) Si hay una solución a la congruencia$3x^2 - y^2 \equiv -2$ (mod 3), explique por qué entonces debe haber un entero$y$ tal que$y^2 \equiv 2$ (mod 3).
c) Utilizar una prueba por contradicción para probar que la ecuación Diofantina no$3x^2 - y^2 = -2$ tiene solución.
Utilice el método sugerido en el Ejercicio (9) para demostrar que la ecuación Diofantina no$7x^2 + 2 = y^3$ tiene solución.

Exploraciones y actividades
Congruencias Lineales en Una Variable. Dejar$n$ ser un número natural y dejar$a, b \in \mathbb{Z}$ con$a \ne 0$. Una congruencia de la forma$ax \equiv b$ (mod$n$) se denomina congruencia lineal en una variable. Esto se denomina congruencia lineal ya que la variable$x$ se produce a la primera potencia.
Una solución de congruencia lineal en una variable se define de manera similar a la solución de una ecuación. Una solución es un número entero que hace que la congruencia resultante sea verdadera cuando el entero es sustituido por la variable$x$. Por ejemplo,

$\bullet$ El entero$x = 3$ es una solución para la congruencia$2x \equiv 1$ (mod 5) ya que$2 \cdot 3 \equiv 1$ (mod 5) es una verdadera congruencia.
$\bullet$El entero$x = 7$ es una solución para la congruencia$3x \equiv 1$ (mod 6) ya que$3 \cdot 7 \equiv 1$ (mod 6) no es una verdadera congruencia.

(a) Verificar que$x = 2$ y$x = 5$ son las únicas soluciones con las que se encuentra la congruencia lineal$4x \equiv 2$ (mod 6)$0 \le x < 6$.
(b) Demostrar que la congruencia lineal$4x \equiv 3$ (mod 6) no tiene soluciones con$0 \le x < 6$.
(c) Determinar todas las soluciones de la congruencia lineal$3x \equiv 7$ (mod 8) con$0 \le x < 8$.

Las siguientes partes de esta actividad muestran que podemos utilizar los resultados del Teorema 8.22 para ayudar a encontrar todas las soluciones de la congruencia lineal$6x \equiv 4$ (mod 8).

(d) Verificar que$x = 2$ y$x = 5$ son las únicas soluciones con las que la congruencia lineal$6x \equiv 4$ (mod 8)$0 \le x < 8$.
e) Utilizar la definición de “congruencia” para reescribir la congruencia$6x \equiv 4$ (mod 8) en términos de “divide”.
f) Utilizar la definición de “divide” para reescribir el resultado en la parte (11e) en forma de ecuación. (Se debe utilizar un cuantificador existencial.)
(g) Utilizar los resultados de las partes (11d) y (11f) para escribir una ecuación que genere todas las soluciones de la congruencia lineal$6x \equiv 4$ (mod 8).
Pista: Usar Teorema 8.22. Esto puede ser utilizado para generar soluciones para$x$ y la variable introducida en parte (11f). En este caso, sólo nos interesan las soluciones para$x$.

Ahora vamos a$n$ ser un número natural y vamos$a, c \in \mathbb{Z}$ con$a \ne 0$. Una congruencia lineal general de la forma$ax \equiv c$ (mod$n$) se puede manejar de la misma manera que manejamos en$6x \equiv 4$ (mod 8).

h) Utilizar la definición de “congruencia” para reescribir$ax \equiv c$ (mod$n$) en términos de “divide”.
(i) Utilizar la definición de “divide” para reescribir el resultado en la parte (11h) en forma de ecuación. (Se debe utilizar un cuantificador existencial.)
(j) Vamos$d = \text{gcd}(a, n)$. Estado y probar un teorema sobre las soluciones de la congruencia lineal$ax \equiv c$ (mod$n$) en el caso donde$d$ no se divide$c$.
Pista: Usar Teorema 8.22.
(k) Vamos$d = \text{gcd}(a, n)$. Estado y probar un teorema sobre las soluciones de la congruencia lineal$ax \equiv c$ (mod$n$) en el caso donde$d$ divide$c$.

Contestar: Agrega textos aquí. No borre primero este texto.

Vista previa de la actividad\(\PageIndex{1}\): Integer Solutions for Linear Equations in One Variable