4.4: TMS XIII
( \newcommand{\kernel}{\mathrm{null}\,}\)
Como TMS VII #2, este problema es bastante difícil. Ofrece un asombroso ejemplo de aplicación de la técnica geométrica a una cuestión no geométrica.
1 2 gur 2 pi 5 bán de aceite que he comprado. De la compra de 1 shekel de plata,
2 4 silà, cada uno (shekel), de aceite que he cortado.
323 mina de plata como ganancia he visto. Correspondiente a lo
4 he comprado y correspondiente a lo que he vendido?
5 Tú, 4 silà de petróleo posit y 40, (del orden de la) mina, el beneficio posit.
6 igi 40 desprenderse,1′30′′ ya ves,1′30′′ a 4 subir, 6′ ya ves.
76′ a12‵50, el petróleo, sube,1‵17 ya ves.
812 de 4 break, 2 ves, 2 hacen bodega, 4 ves.
9 4 para1‵17 unirse,1‵21 ya ves. ¿Qué es igual? 9 es igual.
10 9 la contraparte postula. 12de 4 que has cortado break, 2 ya ves.
11 2 a la 1ra 9 se unen, 11 ya ves; desde la 2da lágrima,
12 7 ves. 11 silà cada uno (shekel) has comprado, 7 silà has vendido.
13 ¿Plata correspondiente a qué? ¿A qué 11 ¿silà? puedo postular
14 ¿cuál12‵50 de petróleo me da? 1‵10posit, 1 mina 10 shekel de plata.
15 Por 7 silà cada uno (shekel) que vende de petróleo,
16 el de 40 de plata correspondiente a qué? 40 a 7 elevar,
174‵40 ya ves,4‵40 de petróleo.
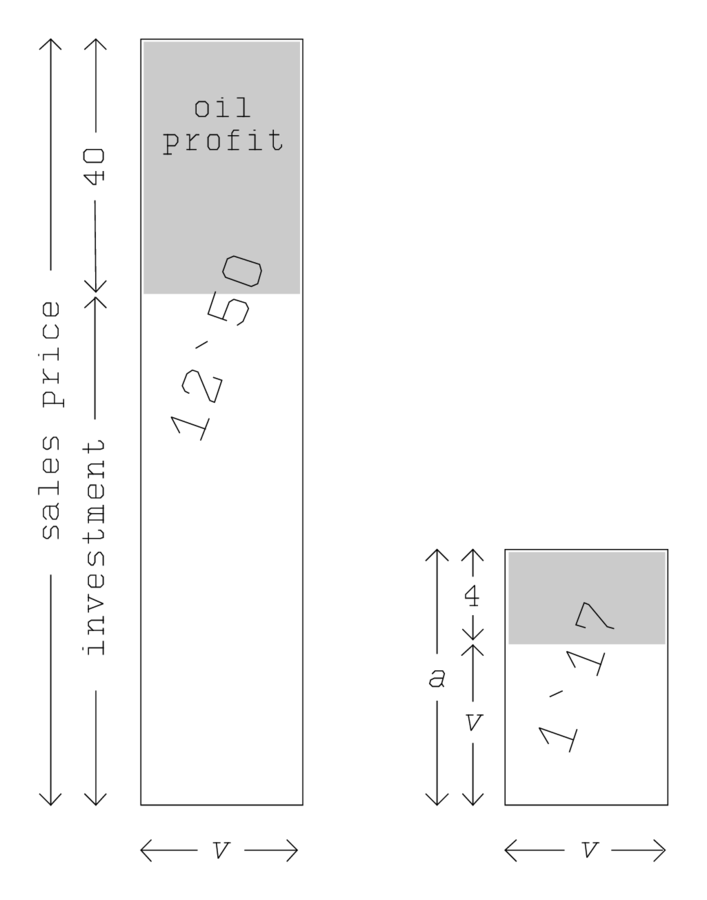
Este es otro problema que, en la lectura superficial, parece reflejar una situación de verdadera vida práctica (aquí, comercial). En una inspección más cercana, sin embargo, resulta ser tan artificial como la anterior pregunta de caña rota: un comerciante ha compradoM=2\mathrm{gur} 2\mathrm{pi} 5\mathrm{bán} (=12‵50 \mathrm{sìla}) de aceite fino (probablemente aceite de sésamo). No se nos dice cuánto pagó, pero el texto nos informa que de la cantidad de petróleo que ha comprado por un shekel (a) ha cortado 4 sìla, vendiendo lo que quedaba (v=a-4) por 1 shekel;a yv son así los recíprocos de los dos precios —podemos hablar de ellos como “tarifas” de compra y venta. Además, el beneficio totalw asciende a\frac{2}{3} mina = 40 shekel de plata. Para nosotros, familiarizados con el simbolismo de letras algebraicas, es fácil ver que el precio total de compra (la inversión) debe serM \div a, el precio total de ventaM \div v, y la ganancia en consecuenciaw=(M \div v)-(M \div a). Multiplicando pora \cdot v nosotros obtenemos así la ecuación
M \cdot(a-v)=w \cdot a v,
y desde entoncesv=a-4, el sistema
a-v=4 \quad, \quad a \cdot v=(4 M) \div w.
Este sistema —del mismo tipo que el propuesto en YBC 6967, el problema igûm-igibûm (página 46 )— es efectivamente el que se resuelve a partir de la línea 8 en adelante. Sin embargo, desde luego no se ha alcanzado de la manera que acabamos de describir: por un lado porque los babilonios no tenían nuestro simbolismo de carta, por el otro porque entonces habrían encontrado la magnitud(4 M) \div w y no, como realmente lo hacen,(4 \div w) \cdot M.
La señal de su método se vuelve hacia arriba hacia el final del texto. Aquí el texto primero encuentra la inversión total y después la ganancia en petróleo (4`40sìla). Estos cálculos no constituyen una prueba ya que estas magnitudes no se encuentran entre los datos del problema. Tampoco se les pide, sin embargo. Deben ser de interés porque han jugado un papel en la búsqueda de la solución.
La figura 4.8 muestra una interpretación posible y en sus principios plausible. La cantidad total de petróleo está representada por un rectángulo, cuya altura corresponde al precio total de venta en shekel, y cuya amplitud es la “tasa de venta”v (sìla por shekel). El precio total de venta se puede dividir en beneficio (40 shekel) e inversión (precio de compra), y la cantidad de petróleo de manera similar en la ganancia petrolera y la cantidad cuya venta devuelve la inversión.
La relación entre estas dos últimas cantidades debe coincidir con aquella en la que se dividió la cantidad comprada por un shekel, es decir, la relación entre 4 sìla y la que se vende por 1 shekel (asív).
Modificando la escala vertical por un factor que reduce de 40 a 4, es decir, por un factor4 \div w=4 \div 40=6^{\prime}, la inversión se reducirá av, y el área a(4 \div w) \cdot M=1` 17. De esta manera obtenemos el rectángulo a la derecha, para lo cual conocemos el área (a \cdot v=1` 17) y la diferencia entre los lados (a-v=4), exactamente como deberíamos. Además, seguimos el texto en el orden de las operaciones, y el beneficio petrolero así como la inversión juegan un papel importante.
En conjunto, la parte final del procedimiento sigue el modelo de YBC 6967 (y de otros problemas del mismo tipo). La única diferencia ocurre en la línea 10: en lugar de usar el “resto” dela-v que hemos “hecho bodega” en la línea 8,a-v se “rompe” por segunda vez. Eso nos permite “unirnos” primero (lo que se une ya está a disposición) y “arrancar” después.
En YBC 6967, el problema igûm-igibûm (página 46), las cantidades geométricas sirvieron para representar magnitudes de diferente naturaleza, es decir, números abstractos. Aquí, la representación es más sutil: un segmento representa una cantidad de plata, el otro la cantidad de petróleo correspondiente a un shekel de plata.


