1.2: La Ecuación Logística
- Page ID
- 117614
La ecuación logística
La ley de crecimiento exponencial para el tamaño de la población es poco realista a lo largo de largos tiempos. Eventualmente, el crecimiento será verificado por el consumo excesivo de recursos. Suponemos que el ambiente tiene una capacidad intrínseca de carga\(K\), y poblaciones mayores que este tamaño experimentan tasas de mortalidad elevadas.
Para modelar el crecimiento poblacional con una capacidad de carga ambiental\(K\), buscamos una ecuación no lineal de la forma
\[\frac{d N}{d t}=r N F(N) \nonumber \]
donde\(F(N)\) proporciona un modelo de regulación ambiental. Esta función debe satisfacer\(F(0)=1\) (la población crece exponencialmente con la tasa de crecimiento\(r\) cuando\(N\) es pequeña),\(F(K)=0\) (la población deja de crecer a la capacidad de carga), y\(F(N)<0\) cuando\(N>K\) ( la población decae cuando es mayor que la capacidad de carga). La función más simple que\(F(N)\) satisface estas condiciones es lineal y dada por\(F(N)=1-N / K .\) El modelo resultante es la conocida ecuación logística,
\[\frac{d N}{d t}=r N(1-N / K) \nonumber \]
un modelo importante para muchos procesos además del crecimiento limitado de la población.
Aunque (1.2.2) es una ecuación no lineal, se puede encontrar una solución analítica separando las variables. Antes de embarcarnos en este álgebra, primero ilustramos algunos conceptos básicos utilizados en el análisis de ecuaciones diferenciales no lineales.
Los puntos fijos, también llamados equilibrios, de una ecuación diferencial como (1.2.2) se definen como los valores de\(N\) dónde\(d N / d t=0\). Aquí, vemos que los puntos fijos de (1.2.2) son\(N=0\) y\(N=K .\) Si el valor inicial de\(N\) está en uno de estos puntos fijos, entonces\(N\) permanecerán fijos ahí para siempre. Los puntos fijos, sin embargo, pueden ser estables o inestables. Un punto fijo es estable si una pequeña perturbación del punto fijo decae a cero para que la solución vuelva al punto fijo. Asimismo, un punto fijo es inestable si una pequeña perturbación crece exponencialmente para que la solución se aleje del punto fijo. El cálculo de la estabilidad por medio de pequeñas perturbaciones se denomina análisis de estabilidad lineal. Por ejemplo, considere la ecuación diferencial unidimensional general (usando la notación\(\dot{x}=d x / d t\))
\[\dot{x}=f(x) \nonumber \]
con\(x_{*}\) un punto fijo de la ecuación, es decir\(f\left(x_{*}\right)=0\). Para determinar analíticamente si\(x_{*}\) es un punto fijo estable o inestable, perturbaremos la solución. Escribamos nuestra solución\(x=x(t)\) en el formulario
\[x(t)=x_{*}+\epsilon(t) \nonumber \]
donde inicialmente\(\epsilon(0)\) es pequeño pero diferente de cero. Sustituyendo (1.2.4) en (1.2.3), obtenemos
\[\begin{aligned} \dot{\epsilon} &=f\left(x_{*}+\epsilon\right) \\[4pt] &=f\left(x_{*}\right)+\epsilon f^{\prime}\left(x_{*}\right)+\ldots \\[4pt] &=\epsilon f^{\prime}\left(x_{*}\right)+\ldots, \end{aligned} \nonumber \]
donde la segunda igualdad usa una expansión de la serie Taylor de\(f(x)\) aproximadamente\(x_{*}\) y la tercera igualdad usa\(f\left(x_{*}\right)=0\). Si\(f^{\prime}\left(x_{*}\right) \neq 0\), podemos descuidar términos de orden superior en\(\epsilon\)
para pequeños tiempos, e integrando tenemos
\[\epsilon(t)=\epsilon(0) e^{f^{\prime}\left(x_{*}\right) t} \nonumber \]
La perturbación\(\epsilon(t)\) al punto fijo\(x_{*}\) va a cero según\(f^{\prime}\left(x_{*}\right)<\)\(0 .\) lo\(t \rightarrow \infty\) previsto Por lo tanto, la condición de estabilidad en\(x_{*}\) es
\[x_{*} \text { is } \begin{cases}\text { a stable fixed point if } & f^{\prime}\left(x_{*}\right)<0, \\[4pt] \text { an unstable fixed point if } & f^{\prime}\left(x_{*}\right)>0 .\end{cases} \nonumber \]
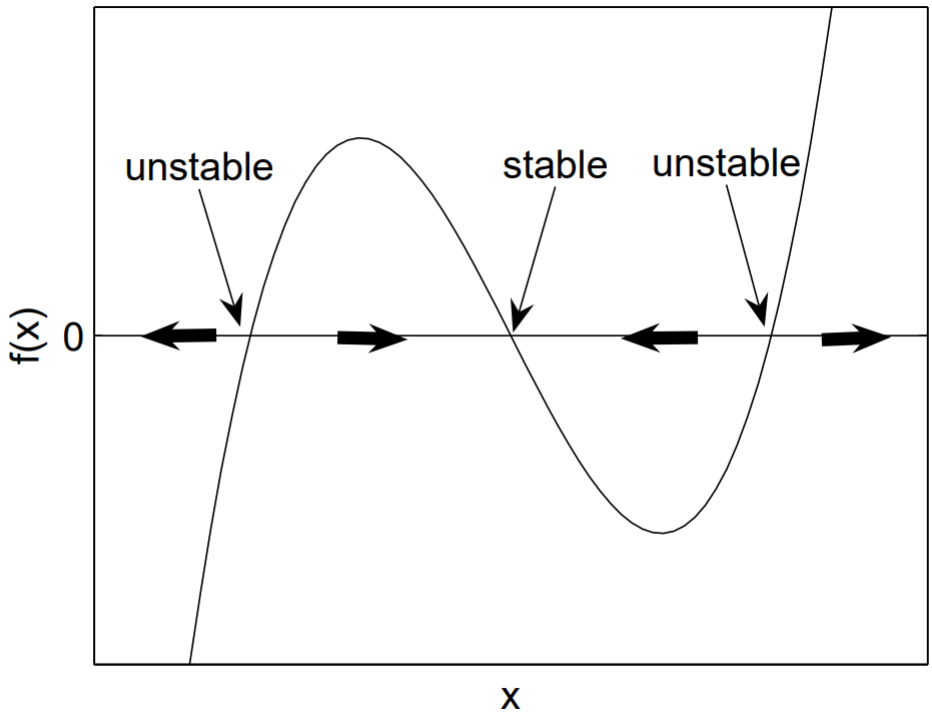
Otro enfoque equivalente pero a veces más sencillo para analizar la estabilidad de los puntos fijos de una ecuación unidimensional no lineal como (1.2.3) es trazar\(f(x)\) versus\(x\). Mostramos un ejemplo genérico en la Fig. 1.1. Los puntos fijos son las\(x\) -intercepciones de la gráfica. Las flechas direccionales en el\(x\) eje -se pueden dibujar en función del signo de\(f(x)\). Si\(f(x)<0\), entonces la flecha apunta a la izquierda; si\(f(x)>0\), entonces la flecha apunta a la derecha. Las flechas muestran la dirección de movimiento de una partícula en posición\(x\) satisfactoria\(\dot{x}=f(x)\). Como se ilustra en la figura 1.1, los puntos fijos con flechas en ambos lados apuntando hacia adentro son estables, y los puntos fijos con flechas en ambos lados apuntando hacia afuera son inestables.
En la ecuación logística (1.2.2), los puntos fijos son\(N_{*}=0, K .\) Un boceto de\(F(N)=\)\(r N(1-N / K)\) versus\(N\), con\(r, K>0\) en la Fig. \(1.2\)inmediatamente muestra que\(N_{*}=0\) es un punto fijo inestable y\(N_{*}=K\) es un punto fijo estable. El enfoque analítico calcula\(F^{\prime}(N)=r(1-2 N / K)\), de manera que\(F^{\prime}(0)=r>0\) y\(F^{\prime}(K)=-r<0\). Nuevamente concluimos que\(N_{*}=0\) es inestable y\(N_{*}=K\) estable.
Ahora resolvemos la ecuación logística analíticamente. Si bien esta ecuación relativamente simple puede resolverse tal cual, primero no dimensionalizamos para ilustrar esta técnica tan importante que luego resultará ser de mayor utilidad. Quizás aquí se pueda adivinar la unidad de tiempo apropiada a ser\(1 / r\) y la unidad apropiada de tamaño poblacional a ser\(K\). Sin embargo, preferimos demostrar una técnica más general que pueda aplicarse de manera útil a ecuaciones para las que las variables adimensionales apropiadas son difíciles de adivinar. Comenzamos por no dimensionalizar el tiempo y el tamaño de la población:
\[\tau=t / t_{*}, \quad \eta=N / N_{*} \nonumber \]
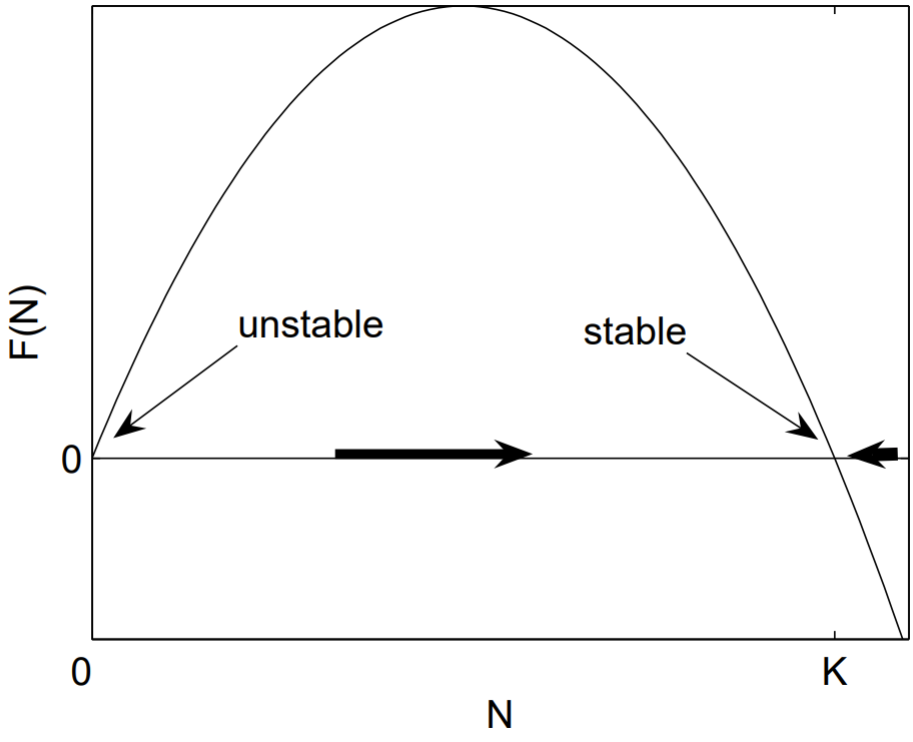
Figura 1.2: Determinación de la estabilidad de los puntos fijos de la ecuación logística.
donde\(t_{*}\) y\(N_{*}\) son unidades dimensionales desconocidas. La derivada\(N\) se calcula como
\[\frac{d N}{d t}=\frac{d\left(N_{*} \eta\right)}{d \tau} \frac{d \tau}{d t}=\frac{N_{*}}{t_{*}} \frac{d \eta}{d \tau} \nonumber \]
Por lo tanto, la ecuación logística (1.2.2) se convierte en
\[\frac{d \eta}{d \tau}=r t_{*} \eta\left(1-\frac{N_{*} \eta}{K}\right), \nonumber \]
que asume la forma más simple con las opciones\(t_{*}=1 / r\) y\(N_{*}=K\). Por lo tanto, nuestras variables adimensionales son
\[\tau=r t, \quad \eta=N / K \nonumber \]
y la ecuación logística, en forma adimensional, se convierte
\[\frac{d \eta}{d \tau}=\eta(1-\eta) \text {, } \nonumber \]
con la condición inicial adimensional\(\eta(0)=\eta_{0}=N_{0} / K\), donde\(N_{0}\) está el tamaño inicial de la población. Obsérvese que la ecuación logística adimensional (1.4) no tiene parámetros libres, mientras que la forma dimensional de la ecuación (1.2.2) contiene\(r\) y\(K\). La reducción en el número de parámetros libres (aquí, dos:\(r\) y\(K\)) por el número de unidades independientes (aquí, también dos: tiempo y tamaño de la población) es una característica general de la no dimensionalización. El resultado teórico se conoce como el Teorema Pi de Buckingham. Reducir el número de parámetros libres en un problema al mínimo absoluto es especialmente importante antes de proceder a una solución numérica. El espacio de parámetros que debe explorarse puede reducirse sustancialmente.
Resolver la ecuación logística adimensional (1.4) puede proceder separando las variables. Separación e integración de\(\tau=0\) a\(\tau\) y\(\eta_{0}\) a\(\eta\) rendimientos
\[\int_{\eta_{0}}^{\eta} \frac{d \eta}{\eta(1-\eta)}=\int_{0}^{\tau} d \tau \nonumber \]
La integral en el lado izquierdo se puede realizar utilizando el método de fracciones parciales:
\[\begin{aligned} \frac{1}{\eta(1-\eta)} &=\frac{A}{\eta}+\frac{B}{1-\eta} \\[4pt] &=\frac{A+(B-A) \eta}{\eta(1-\eta)} \end{aligned} \nonumber \]
y al igualar los coeficientes de los numeradores proporcionales a\(\eta^{0}\) y\(\eta^{1}\), encontramos que\(A=1\) y\(B=1\). Por lo tanto,
\[\begin{aligned} \int_{\eta_{0}}^{\eta} \frac{d \eta}{\eta(1-\eta)} &=\int_{\eta_{0}}^{\eta} \frac{d \eta}{\eta}+\int_{\eta_{0}}^{\eta} \frac{d \eta}{(1-\eta)} \\[4pt] &=\ln \frac{\eta}{\eta_{0}}-\ln \frac{1-\eta}{1-\eta_{0}} \\[4pt] &=\ln \frac{\eta\left(1-\eta_{0}\right)}{\eta_{0}(1-\eta)} \\[4pt] &=\tau \end{aligned} \nonumber \]
Resolviendo para\(\eta\), primero exponenciamos ambos lados y luego aislamos\(\eta:\)
\[\begin{aligned} &\frac{\eta\left(1-\eta_{0}\right)}{\eta_{0}(1-\eta)}=e^{\tau}, \text { or } \quad \eta\left(1-\eta_{0}\right)=\eta_{0} e^{\tau}-\eta \eta_{0} e^{\tau} \\[4pt] &\text { or } \eta\left(1-\eta_{0}+\eta_{0} e^{\tau}\right)=\eta_{0} e^{\tau}, \text { or } \quad \eta=\frac{\eta_{0}}{\eta_{0}+\left(1-\eta_{0}\right) e^{-\tau}} \end{aligned} \nonumber \]
Volviendo a las variables dimensionales, finalmente tenemos
\[N(t)=\frac{N_{0}}{N_{0} / K+\left(1-N_{0} / K\right) e^{-r t}} \nonumber \]
Hay varias formas de escribir el resultado final dado por (1.5). La presentación de un resultado matemático requiere un buen sentido estético y es un elemento importante de la técnica matemática. Al decidir cómo escribir (1.5), consideré si era fácil observar los siguientes resultados limitantes: (1)\(N(0)=N_{0} ;(2) \lim _{t \rightarrow \infty} N(t)=K\); y (3)\(\lim _{K \rightarrow \infty} N(t)=N_{0} \exp (r t)\)
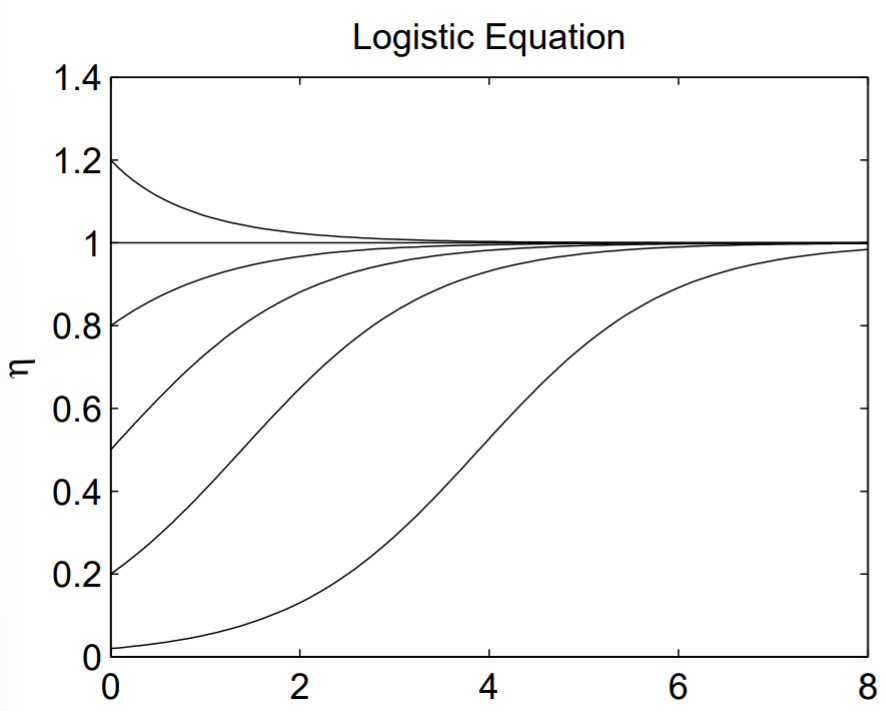
En la Fig. 1.3, trazamos la solución a la ecuación logística adimensional para las condiciones iniciales\(\eta_{0}=0.02,0.2,0.5,0.8,1.0\), y\(1.2\). La curva más baja es la característica 'forma de S' generalmente asociada con la solución de la ecuación logística. Esta curva sigmoidal aparece en muchos otros tipos de modelos. El script de MATLAB para producir la Fig. \(1.3\)se muestra a continuación.
