3.4: Aplicaciones
- Page ID
- 116953
Interés Compuesto
La ecuación para el crecimiento de una inversión con capitalización continua de interés es una ecuación diferencial de primer orden. \(S(t)\)Sea el valor de la inversión en el momento\(t\), y deje\(r\) ser la tasa de interés anual compuesta después de cada intervalo de tiempo\(∆t\). También podemos incluir depósitos (o retiros). \(k\)Sea el monto del depósito anual, y supongamos que se deposita una cuota después de cada intervalo de tiempo\(∆t\). El valor de la inversión en el momento\(t + ∆t\) se da entonces por \[\label{eq:1}S(t+\Delta t)=S(t)+(r\Delta t)S(t)+k\Delta t,\]donde al final del intervalo de tiempo\(∆t\),\(r\Delta tS(t)\) es la cantidad de intereses acreditados y\(k∆t\) es la cantidad de dinero depositado\((k > 0)\) o retirado\((k < 0)\). Como ejemplo numérico, si la cuenta mantenida\($10,000\) en tiempo\(t\), y\(r = 6\%\) por año y\(k = $12,000\) por año, digamos, y el período de capitalización y depósito es\(∆t = 1\text{ month} = 1/12\text{ year}\), entonces el interés otorgado después de un mes es\(r\Delta tS = (0.06/12) × $10,000 = $50\), y el monto depositado es\(k∆t = $1000\).
Reordenando los términos de\(\eqref{eq:1}\) para exhibir lo que pronto se convertirá en un derivado, tenemos\[\frac{S(t+\Delta t)-S(t)}{\Delta t}=rS(t)+k.\nonumber\]
La ecuación para la composición continua de intereses y depósitos continuos se obtiene tomando el límite\(\Delta t\to 0\). La ecuación diferencial resultante es la \[\label{eq:2}\frac{dS}{dt}=rS+k,\]que se puede resolver con la condición inicial\(S(0) = S_0\), donde\(S_0\) está el capital inicial. Podemos resolver ya sea separando variables o usando un factor integrador; resuelvo aquí separando variables. Integrando de\(t = 0\) a un tiempo final\(t\), \[\begin{align} \int_{S_0}^S \frac{dS}{rS+k}&=\int_0^tdt,\nonumber \\ \frac{1}{r}\ln\left(\frac{rS+k}{rS_0+k}\right)&=t,\nonumber \\ rS+k&=(rS_0+k)e^{rt},\nonumber \\ S&=\frac{rS_0e^{rt}+ke^{rt}-k}{r},\nonumber \\ S&=S_0e^{rt}+\frac{k}{r}e^{rt}(1-e^{-rt}),\label{eq:3} \end{align}\]donde el primer término en el lado derecho de\(\eqref{eq:3}\) proviene del capital invertido inicial, y el segundo plazo proviene de los depósitos (o retiros). Evidentemente, la capitalización da como resultado el crecimiento exponencial de una inversión.
Como ejemplo práctico, podemos analizar un plan de retiro simple. Es más fácil suponer que todos los montos y rendimientos están en dólares reales (ajustados por inflación). Supongamos que un\(25\) niño de un año planea apartar una cantidad fija cada año de su vida laboral, invierte a un retorno real de\(6\%\), y se jubila a la edad\(65\). ¿Cuánto debe invertir cada año para tener\(\text{HK }$8,000,000\) al jubilarse? (Nota:\(\text{US }$1\approx\text{ HK }$8\).) Tenemos que resolver\(\eqref{eq:3}\) para\(k\) usar\(t = 40\text{ years}\),\(S(t) = $8,000,000\),\(S_0 = 0\), y\(r = 0.06\) por año. Tenemos\[\begin{aligned}k&=\frac{rS(t)}{e^{rt}-1}, \\ k&=\frac{0.06\times 8,000,000}{e^{0.06\times 40}-1}, \\ &=$47,889\text{ year}^{-1}.\end{aligned}\]
Para haber ahorrado aproximadamente un millón\(\text{US}$\) al jubilarse, el trabajador necesitaría ahorrar aproximadamente\(\text{HK }$50,000\) al año a lo largo de su vida laboral. Tenga en cuenta que el monto ahorrado a lo largo de la vida del trabajador es aproximadamente\(40 × $50,000 = $2,000,000\), mientras que el monto ganado por la inversión (al rendimiento\(6\%\) real supuesto) es aproximadamente\($8,000,000 − $2,000,000 = $6,000,000\). El monto ganado de la inversión es sobre\(3×\) el monto ahorrado, incluso con el modesto retorno real de\(6\%\). La planificación de inversiones bien merece la pena el esfuerzo.
Reacciones Químicas
Supongamos que dos químicos\(A\) y\(B\) reaccionan para formar un producto\(C\), el cual escribimos un\[A+B\overset{k}{\to}C,\nonumber\] where\(k\) se llama la constante de velocidad de la reacción. Por simplicidad, usaremos el mismo símbolo\(C\), digamos, para referirnos tanto al químico\(C\) como a su concentración. La ley de acción masiva dice que\(dC/dt\) es proporcional al producto de las concentraciones\(A\) y\(B\), con proporcionalidad constante\(k\); es decir \[\label{eq:4}\frac{dC}{dt}=kAB.\]
De igual manera, la ley de acción de masas permite escribir ecuaciones para las derivadas del tiempo de las concentraciones de reactivos\(A\) y\(B\):
\[\label{eq:5}\frac{dA}{dt}=-kAB,\quad\frac{dB}{dt}=-kAB.\]
La oda dada por\(\eqref{eq:4}\) puede resolverse analíticamente usando leyes de conservación. Suponemos que\(A_0\) y\(B_0\) son las concentraciones iniciales de los reactivos, y que ningún producto está inicialmente presente. Desde\(\eqref{eq:4}\) y\(\eqref{eq:5}\),\[\begin{array}{lll} \frac{d}{dt}(A+C)=0&\Longrightarrow &A+C=A_0, \\ \frac{d}{dt}(B+C)=0&\Longrightarrow &B+C=B_0.\end{array}\nonumber\]
Usando estas leyes de conservación,\(\eqref{eq:4}\) se convierte en\[\frac{dC}{dt}=k(A_0-C)(B_0-C),\quad C(0)=0,\nonumber\] lo que es una ecuación no lineal que puede integrarse separando variables. Separando e integrando, obtenemos \[\begin{align}\int_0^C\frac{dC}{(A_0-C)(B_0-C)}&=k\int_0^t dt\nonumber \\ &=kt.\label{eq:6}\end{align}\]
La integral restante se puede hacer usando el método de fracciones parciales. Escribimos \[\label{eq:7}\frac{1}{(A_0-C)(B_0-C)}=\frac{a}{A_0-C}+\frac{b}{B_0-C}.\]
El método de encubrimiento es el método más sencillo para determinar los coeficientes desconocidos\(a\) y\(b\). Para determinar\(a\), multiplicamos ambos lados de\(\eqref{eq:7}\) por\(A_0 − C\) y establecemos\(C = A_0\) para encontrar\[a=\frac{1}{B_0-A_0}.\nonumber\]
Del mismo modo, para determinar\(b\), multiplicamos ambos lados de\(\eqref{eq:7}\) por\(B_0 − C\) y establecemos\(C = B_0\) para encontrar\[b=\frac{1}{A_0-B_0}.\nonumber\]
Por lo tanto,\[\frac{1}{(A_0-C)(B_0-C)}=\frac{1}{B_0-A_0}\left(\frac{1}{A_0-C}-\frac{1}{B_0-C}\right),\nonumber\] y la integral restante de\(\eqref{eq:6}\) se convierte (usando\(C < A_0,\: B_0\))\[\begin{aligned} \int_0^C\frac{dC}{(A_0-C)(B_0-C)}&=\frac{1}{B_0-A_0}\left(\int_0^C\frac{dC}{A_0-C}-\int_0^C\frac{dC}{B_0-C}\right) \\ &=\frac{1}{B_0-A_0}\left(-\ln\left(\frac{A_0-C}{A_0}\right)+\ln\left(\frac{B_0-C}{B_0}\right)\right) \\ &=\frac{1}{B_0-A_0}\ln\left(\frac{A_0(B_0-C)}{B_0(A_0-C)}\right).\end{aligned}\]
Usando esta integral en\(\eqref{eq:6}\), multiplicando por\((B_0 − A_0)\) y exponenciando, obtenemos\[\frac{A_0(B_0-C)}{B_0(A_0-C)}=e^{(B_0-A_0)kt}.\nonumber\]
Resolviendo para\(C\), finalmente obtenemos\[C(t)=A_0B_0\frac{e^{(B_0-A_0)kt}-1}{B_0e^{(B_0-A_0)kt}-A_0},\nonumber\] lo que parece ser una expresión complicada, pero tiene los límites simples\[\begin{aligned}\underset{t\to\infty}{\lim}C(t)&=\left\{\begin{array}{ll}A_0,&\text{if }A_0<B_0, \\ B_0,&\text{if }B_0<A_0\end{array}\right. \\ &=\text{min}(A_0,B_0).\end{aligned}\]
Como cabría esperar, la reacción se detiene después de que uno de los reactivos se agota; y la concentración final de producto es igual a la concentración inicial del reactivo agotado.
Velocidad terminal
Usando la ley de Newton, modelamos una masa\(m\) libre que cae bajo gravedad pero con resistencia al aire. Suponemos que la fuerza de resistencia del aire es proporcional a la velocidad de la masa y se opone a la dirección del movimiento. Definimos el\(x\) eje -para apuntar en dirección ascendente, opuesto a la fuerza de la gravedad. Cerca de la superficie de la Tierra, la fuerza de gravedad es aproximadamente constante y viene dada por\(−mg\), con\(g = 9.8\text{m/s}^2\) la aceleración gravitacional habitual. La fuerza de resistencia del aire es modelada por\(−kv\), donde\(v\) está la velocidad vertical de la masa y\(k\) es una constante positiva. Cuando la masa está cayendo,\(v < 0\) y la fuerza de resistencia del aire es positiva, apuntando hacia arriba y oponiéndose al movimiento. Por lo tanto, la fuerza total sobre la masa viene dada por\(F = −mg − kv\). Con\(F = ma\) y\(a = dv/dt\), obtenemos la ecuación diferencial \[\label{eq:8}m\frac{dv}{dt}=-mg-kv.\]
La velocidad terminal\(v_∞\) de la masa se define como la velocidad asintótica después de que la resistencia del aire equilibre la fuerza gravitacional. Cuando la masa está a velocidad terminal, de\(dv/dt = 0\) modo que \[\label{eq:9}v_{\infty}=-\frac{mg}{k}.\]
El acercamiento a la velocidad terminal de una masa inicialmente en reposo se obtiene resolviendo\(\eqref{eq:8}\) con condición inicial\(v(0) = 0\). La ecuación es tanto lineal como separable, y resuelvo separando variables:
\[\begin{aligned}m\int_0^v\frac{dv}{mg+kv}&=-\int_0^t dt,\\ \frac{m}{k}\ln\left(\frac{mg+kv}{mg}\right)&=-t, \\ 1+\frac{kv}{mg}&=e^{-kt/m}, \\ v&=-\frac{mg}{k}\left(1-e^{-kt/m}\right).\end{aligned}\]
Por lo tanto\(v = v_∞\left( 1 − e^{−kt/m}\right)\),, y\(v\) se acerca a\(v_∞\) medida que el término exponencial decae a cero.
A modo de ejemplo, un paracaidista de masa\(m = 100\text{ kg}\) con su paracaídas cerrado puede tener una velocidad terminal de\(200\text{ km/hr}\). Con\[g=(9.8\text{ m/s}^2)(10^{-3}\text{ km/m})(60\text{ s/min})^2(60\text{ min/hr})^2=127,008\text{ km/hr}^2,\nonumber\] uno obtiene de\(\eqref{eq:9}\),\(k = 63, 504\text{ kg/hr}\). Por lo tanto, la mitad de la velocidad terminal para caída libre (\(100\text{ km/hr}\)) se alcanza cuando\((1 − e^{−kt/m}) = 1/2\), o\(t = m \ln 2/k\approx 4\text{ sec}\). Aproximadamente\(95\%\) de la velocidad terminal (\(190\text{ km/hr}\)) se alcanza después\(17\text{ sec}\).
Velocidad de escape
Un problema físico interesante es encontrar la velocidad inicial más pequeña para que una masa en la superficie de la Tierra escape del campo gravitacional de la Tierra, la llamada velocidad de escape. La ley de gravitación universal de Newton afirma que la fuerza gravitacional entre dos cuerpos masivos es proporcional al producto de las dos masas e inversamente proporcional al cuadrado de la distancia entre ellos. Para una masa\(m\) una posición\(x\) por encima de la superficie de la Tierra, la fuerza sobre la masa viene dada por\[F=-G\frac{Mm}{(R+x)^2},\nonumber\] donde\(M\) y\(R\) son la masa y radio de la Tierra y\(G\) es la constante gravitacional. El signo menos significa que la fuerza sobre los\(m\) puntos de masa en la dirección de la disminución\(x\). La aceleración aproximadamente constante\(g\) en la superficie terrestre corresponde al valor absoluto de\(F/m\) cuando\(x = 0\):
\[g=\frac{GM}{R^2},\nonumber\]y\(g\approx 9.8\text{ m/s}^2\). Así pues, la ley de Newton\(F = ma\) para la masa\(m\) viene dada por \[\begin{align}\frac{d^2x}{dt^2}&=-\frac{GM}{(R+x)^2}\nonumber \\ &=-\frac{g}{(1+x/R)^2},\label{eq:10}\end{align}\]donde se sabe que está el radio de la Tierra\(R\approx 6350\text{ km}\).
Un truco útil nos permite resolver esta ecuación diferencial de segundo orden como una ecuación de primer orden. Primero, tenga en cuenta eso\(d^2x/dt^2 = dv/dt\). Si escribimos\(v(t) = v(x(t))\) —considerando que la velocidad de la masa\(m\) es una función de su distancia sobre la Tierra— tenemos usando la regla de la cadena\[\begin{aligned}\frac{dv}{dt}&=\frac{dv}{dx}\frac{dx}{dt} \\ &=v\frac{dv}{dx},\end{aligned}\] donde hemos usado\(v = dx/dt\). Por lo tanto,\(\eqref{eq:10}\) se convierte en la oda de primer orden\[v\frac{dv}{dx}=-\frac{g}{(1+x/R)^2},\nonumber\] que puede resolverse asumiendo una velocidad inicial\(v(x = 0) = v_0\) cuando la masa se dispara verticalmente desde la superficie de la Tierra. Separando variables e integrando, obtenemos\[\int_{v_0}^v vdv=-g\int_0^x\frac{dx}{(1+x/R)^2}.\nonumber\]
La integral izquierda es\(\frac{1}{2}(v^2 − v_0^2)\), y la integral derecha se puede realizar usando la sustitución\(u = 1 + x/R\),\(du = dx/R\):
\[\begin{aligned}\int_0^x\frac{dx}{(1+x/R)^2}&=R\int_1^{1+x/R}\frac{du}{u^2} \\ &=-\left.\frac{R}{u}\right]_1^{1+x/R} \\ &=R-\frac{R^2}{x+R} \\ &=\frac{Rx}{x+R}.\end{aligned}\]
Por lo tanto,\[\frac{1}{2}(v^2-v_0^2)=-\frac{gRx}{x+R},\nonumber\] que al multiplicarse por\(m\) es una expresión de la conservación de la energía (el cambio de la energía cinética de la masa es igual al cambio en la energía potencial). Resolviendo para\(v^2\),\[v^2=v_0^2-\frac{2gRx}{x+R}.\nonumber\]
La velocidad de escape se define como la velocidad inicial mínima\(v_0\) tal que la masa puede escapar al infinito. Por lo tanto,\(v_0 = v_{\text{escape}}\) cuando\(v → 0\) como\(x → ∞\). Tomando este límite, tenemos\[\begin{aligned}v_{\text{escape}}^2&=\underset{x\to\infty}{\lim}\frac{2gRx}{x+R} \\ &=2gR.\end{aligned}\]
Con\(R\approx 6350\text{ km}\) y\(g = 127 008\text{ km/hr}^2\), determinamos\(v_{\text{escape}} = \sqrt{2gR}\approx 40 000\text{ km/hr}\). En comparación, la velocidad del hocico de un rifle moderno de alto rendimiento es\(4300\text{ km/hr}\), casi un orden de magnitud demasiado lenta para que una bala, disparada al cielo, pueda escapar de la gravedad de la Tierra.
Circuito RC
Considere una resistencia\(R\) y un condensador\(C\) conectados en serie como se muestra en la Fig. \(\PageIndex{1}\). Una batería que proporciona una fuerza electromotriz, o emf\(\mathcal{E}\), se conecta a este circuito mediante un interruptor. Inicialmente, no hay carga en el condensador. Cuando el interruptor se lanza a una, la batería se conecta y el condensador se carga. Cuando se lanza el interruptor a\(b\), la batería se desconecta y el condensador se descarga, con la energía disipada en la resistencia. Aquí, determinamos la caída de voltaje a través del condensador durante la carga y descarga.
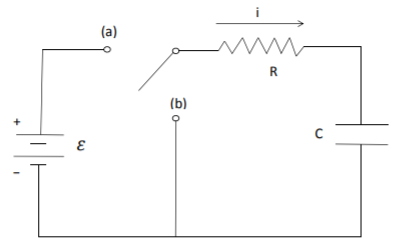
Las ecuaciones para las caídas de voltaje a través de un condensador y una resistencia están dadas por \[\label{eq:11} V_C=q/C,\quad V_R=iR,\]dónde\(C\) está la capacitancia y\(R\) es la resistencia. El cargo\(q\) y la corriente\(i\) están relacionados por \[\label{eq:12}i=\frac{dq}{dt}.\]
La ley de voltaje de Kirchhoff establece que la emf\(\mathcal{E}\) en cualquier bucle cerrado es igual a la suma de las caídas de voltaje en ese bucle. Aplicar la ley de voltaje de Kirchhoff cuando se lanza el interruptor a\(a\) resulta en \[\label{eq:13}V_R+V_C=\mathcal{E}.\]
Usando\(\eqref{eq:11}\) y\(\eqref{eq:12}\), la caída de voltaje a través de la resistencia se puede escribir en términos de la caída de voltaje a través del condensador como\[V_R=RC\frac{dV_C}{dt},\nonumber\] y se\(\eqref{eq:13}\) puede reescribir para producir la ecuación diferencial lineal de primer orden para VC dada por \[\label{eq:14}\frac{dV_C}{dt}+V_C/RC=\mathcal{E}/RC,\]con condición inicial \(V_C(0)=0.\)
El factor integrador para esta ecuación es\[\mu(t)=e^{t/RC},\nonumber\] y\(\eqref{eq:14}\) se integra\[V_C(t)=e^{-t/RC}\int_0^t(\mathcal{E}/RC)e^{t/RC}dt,\nonumber\] con la solución\[V_C(t)=\mathcal{E}\left(1-e^{-t/RC}\right).\nonumber\]
El voltaje comienza en cero y se eleva exponencialmente a\(\mathcal{E}\), con escala de tiempo característica dada por\(RC\).
Cuando se lanza el interruptor a\(b\), la aplicación de la ley de voltaje de Kirchhoff da como resultado la ecuación diferencial correspondiente\[V_R+V_C=0,\nonumber\]\[\frac{dV_C}{dt}+V_C/RC=0.\nonumber\]
Aquí, suponemos que la capacitancia está inicialmente completamente cargada de tal manera que\(V_C(0) =\mathcal{E}\). La solución, entonces, durante la fase de descarga viene dada por\[V_C(t)=\mathcal{E}e^{-t/RC}.\nonumber\]
El voltaje comienza en\(\mathcal{E}\) y decae exponencialmente a cero, nuevamente con la escala de tiempo característica dada por\(RC\).
La Ecuación Logística
Dejar\(N(t)\) ser el número de individuos en una población a la vez\(t\), y dejar\(b\) y\(d\) ser la tasa media de natalidad per cápita y la tasa de mortalidad, respectivamente. En poco tiempo\(∆t\), el número de nacimientos en la población es\(b\Delta tN\), y el número de muertes es\(d\Delta tN\). Entonces\(t + ∆t\) se determina que una ecuación para\(N\) en el tiempo es la\[N(t+\Delta t)=N(t)+b\Delta tN(t)-d\Delta tN(t),\nonumber\] que se puede reorganizar a\[\frac{N(t+\Delta t)-N(t)}{\Delta t}=(b-d)N(t);\nonumber\] y como\(\Delta t\to 0\), y con\(r=b-d\), tenemos\[\frac{dN}{dt}=rN.\nonumber\]
Este es el modelo de crecimiento maltusiano (Thomas Malthus, 1766-1834), y es la misma ecuación que nuestro modelo de interés compuesto.
Bajo un modelo de crecimiento maltusiano, el tamaño de la población crece exponencialmente como\[N(t)=N_0e^{rt},\nonumber\] donde\(N_0\) está el tamaño inicial de la población. Sin embargo, cuando el crecimiento poblacional está limitado por recursos limitados, una modificación heurística al modelo de crecimiento maltusiano da como resultado la ecuación de Verhulst, \[\label{eq:15}\frac{dN}{dt}=rN\left(1-\frac{N}{K}\right),\]donde\(K\) se llama la capacidad de carga del ambiente. Hacer\(\eqref{eq:15}\) adimensional usando\(\tau = rt\) y\(x = N/K\) conduce a la ecuación logística,\[\frac{dx}{d\tau}=x(1-x),\nonumber\] donde podemos asumir la condición inicial\(x(0) = x_0 > 0\). Separación de variables e integración\[\int_{x_0}^x\frac{dx}{x(1-x)}=\int_0^{\tau}d\tau .\nonumber\]
La integral en el lado izquierdo se puede hacer usando el método de fracciones parciales:
\[\frac{1}{x(1-x)}=\frac{a}{x}+\frac{b}{1-x},\nonumber\]y los rendimientos del método de encubrimiento\(a = b = 1\). Por lo tanto,\[\begin{aligned}\int_{x_0}^x\frac{dx}{x(1-x)}&=\int_{x_0}^x\frac{dx}{x}+\int_{x_0}^x\frac{dx}{(1-x)} \\ &=\ln\frac{x}{x_0}-\ln\frac{1-x}{1-x_0} \\ &=\ln\frac{x(1-x_0)}{x_0(1-x)} \\ &=\tau .\end{aligned}\]
Resolviendo para\(x\), primero exponenciamos ambos lados y luego aislamos\(x\):
\[\begin{align}\frac{x(1-x_0)}{x_0(1-x)}&=e^{\tau},\nonumber \\ x(1-x_0)&=x_0e^{\tau}-xx_0e^{\tau},\nonumber \\ x(1-x_0+x_0e^{\tau})&=x_0e^{\tau},\nonumber \\ x&=\frac{x_0}{x_0+(1-x_0)e^{-\tau}}.\label{eq:16}\end{align}\]
Observamos que para\(x_0 > 0\), tenemos\(\lim_{\tau\to\infty} x(\tau ) = 1\), correspondiente a\[\underset{t\to\infty}{\lim}N(t)=K.\nonumber\]
La población, por lo tanto, crece en tamaño hasta alcanzar la capacidad de carga de su entorno.