2.7: El tamaño de la cría de un gusano hermafrodita
- Page ID
- 117574
Caenorhabditis elegans, un gusano nematodo que habita\(1 \mathrm{~mm}\) en el suelo, es un organismo modelo ampliamente estudiado en biología. Con un cuerpo compuesto de aproximadamente
1000 células, es uno de los organismos multicelulares más simples bajo estudio. Los avances en la comprensión del desarrollo de este organismo multicelular llevaron a la concesión del premio Nobel de Fisiología o Medicina 2002 a los tres biólogos de C. elegans Sydney Brenner, H. Robert Horvitz y John E. Sulston.
El gusano C. elegans tiene dos sexos: los hermafroditas, que son esencialmente hembras que pueden producir espermatozoides internos y autofertilizar sus propios óvulos, y los machos, que deben aparearse con hermafroditas para producir descendencia. En cultivos de laboratorio, los machos son raros y los gusanos generalmente se propagan por autofertilización. Por lo general, un hermafrodita pone alrededor de óvulos\(250-350\) autofecundados antes de volverse infértil. Es razonable suponer que las fuerzas de selección natural han dado forma a la historia de vida de C. elegans, y que el número de crías producidas por un hermafrodita autofecundante debe ser en cierto sentido óptimo. Aquí, mostramos cómo un modelo estructurado por edad aplicado a C. elegans produce ideas teóricas sobre el tamaño de cría de un hermafrodita autofecundante.
Para desarrollar un modelo matemático para C. elegans, necesitamos conocer algunos detalles de su historia de vida. Como primera aproximación (Barker, 1992), en la Fig. 2.5 se muestra una línea de tiempo simplificada de la vida de un hermafrodita. El óvulo fertilizado se pone a la vez\(t=0\). Durante un periodo de crecimiento juvenil, el gusano inmaduro se desarrolla a través de cuatro estadios larvarios (L1-L4). Hacia el final de L4 y por poco tiempo después de su muda final a la edad adulta, el hermafrodita produce esperma, que luego se almacena para su uso posterior. Entonces la hermafrodita produce óvulos, los autofertiliza usando su esperma almacenado internamente, y los pone. En ausencia de machos, cesa la producción de óvulos después de que se utilicen todos los espermatozoides. Suponemos que el período de crecimiento juvenil ocurre durante\(0<t<g\), la espermatogénesis ocurre durante\(g<t<g+s\), y la producción de huevos, autofecundación y puesta de huevos ocurre durante\(g+s<t<g+s+e\).
Aquí, queremos entender por qué los hermafroditas limitan su producción de esperma. Los biólogos definen a machos y hembras a partir del tamaño y costo metabólico de sus gametos: los espermatozoides son pequeños y baratos y los óvulos son grandes y caros. Entonces a primera vista, es desconcertante por qué el número total de crías producidas por un hermafrodita está limitado por el número de espermatozoides producidos, más que por el número de óvulos. Debe haber un costo oculto para el hermafrodita de producir esperma adicional distinto al metabólico. Para entender la biología básica, es instructivo considerar dos casos limitantes: (1) no producción de esperma; (2) producción infinita de esperma. En ambos casos, el hermafrodita no produce descendencia en el primer caso porque no hay espermatozoides, y en el segundo porque no hay óvulos. El número de espermatozoides producidos por un hermafrodita antes de poner óvulos es por lo tanto un compromiso; aunque más espermatozoides significa más descendencia, más espermatozoides también significa retraso en la producción de óvulos.
Nuestra principal suposición teórica es que la selección natural favorecerá a los gusanos con la capacidad de establecer poblaciones con el mayor parámetro maltusiano\(r\). Los gusanos que contienen una mutación genética que resulta en un valor mayor para eventualmente\(r\) saldrán-
| \(g\) | periodo de crecimiento | \(72 \mathrm{~h}\) |
|---|---|---|
| \(s\) | período de producción de esperma | \(11.9 \mathrm{~h}\) |
| \(e\) | periodo de producción de huevos | \(65 \mathrm{~h}\) |
| \(p\) | tasa de producción de esperma | \(24 \mathrm{~h}^{-1}\) |
| \(m\) | tasa de producción de huevos | \(4.4 \mathrm{~h}^{-1}\) |
| \(B\) | tamaño de cría | 286 |
Cuadro 2.3: Parámetros en un modelo de historia de vida de C. elegans, con estimaciones experimentales.
numerar todos los demás gusanos.
Los parámetros que necesitamos para nuestro modelo matemático se listan en Tabla\(2.3\), junto con los valores experimentales estimados (Cutter, 2004). Además del periodo de crecimiento\(g\), periodo de producción de esperma y periodo\(s\) de producción de óvulos\(e\) (todo en unidades de horas), necesitamos la tasa de producción de esperma\(p\) y la tasa de producción de óvulos\(m\) (ambas en unidades de horas inversas). También definimos el tamaño de cría\(B\) como el número total de huevos fertilizados puestos por un hermafrodita autofecundante. El tamaño de la cría es igual al número de espermatozoides producidos, y también igual al número de óvulos puestos, de manera que
\[B=p s=m e \nonumber \]
Podemos utilizar (2.7.1) para eliminar\(s\) y\(e\) a favor de\(B\):
\[s=B / p, \quad e=B / m \nonumber \]
La ecuación continua de Euler-Lotka (2.6.7) para\(r\) requiere un modelo para\(f(a)=\)\(m(a) l(a)\), donde\(m(a)\) está la función de maternidad específica por edad y\(l(a)\) es la función de supervivencia específica por edad. La función\(l(a)\) satisface la ecuación diferencial (2.6.11), y aquí hacemos la suposición simplificadora de que la función de mortalidad específica por edad\(\mu(a)=d\), donde\(d\) es la tasa de mortalidad per cápita independiente de la edad. Implícitamente, estamos asumiendo que los gusanos no mueren de vejez durante la puesta de huevos, sino que mueren de depredación, inanición, enfermedad u otras causas independientes de la edad. Tal suposición es razonable ya que los gusanos pueden vivir en el laboratorio durante varias semanas después del agotamiento de los espermatozoides. Resolver\((2.6.11)\) con la condición inicial\(l(0)=1\) da como resultado
\[l(a)=\exp (-d \cdot a) \nonumber \]
La función de maternidad específica por edad\(m(a)\) se define de tal manera que\(m(a) \Delta a\) es el número esperado de crías producidas durante el intervalo de edad\(\Delta a\). Suponemos que un hermafrodita pone huevos a un ritmo constante a lo\(m\) largo de las edades\(g+s<a<g+s+e\); por lo tanto,
\[m(a)= \begin{cases}m & \text { for } g+s<a<g+s+e \\[4pt] 0 & \text { otherwise }\end{cases} \nonumber \]
Usando\((2.7.2),(2.7.3)\) y\((2.7.4)\), la ecuación continua de Euler-Lotka (2.6.7) para el parámetro maltusiano\(r\) se convierte en
\[\int_{g+B / p}^{g+B / p+B / m} m \exp [-(r+d) a] d a=1 \nonumber \]
Integrando,
\[\begin{aligned} 1 &=\int_{g+B / p}^{g+B / p+B / m} m \exp [-(r+d) a] d a \\[4pt] &=\frac{m}{r+d}\{\exp [-(g+B / p)(r+d)]-\exp [-(g+B / p+B / m)(r+d)]\} \\[4pt] &=\frac{m}{r+d} \exp [-(g+B / p)(r+d)]\{1-\exp [-(B / m)(r+d)]\} \end{aligned} \nonumber \]
que puede ser reescrito como
\[(r+d) \exp [(g+B / p)(r+d)]=m\{1-\exp [-(B / m)(r+d)]\} \nonumber \]
Con los parámetros\(d, g, p\), y\(m\) fijos, la ecuación integrada de Euler-Lotka (2.7.6) es una ecuación implícita para\(r=r(B)\).
Para demostrar que\(r=r(B)\) tiene un máximo a algún valor de\(B\), resolvemos numéricamente (2.7.6) para\(r\) con los valores de los parámetros de\(g, p\) y\(m\) obtenidos de Table\(2.3\). Ya que\(r+d\) es máximo al mismo valor de\(B\) eso\(r\) es máximo, y\(d\) sólo entra (2.7.6) en la forma\(r+d\), sin pérdida de generalidad podemos tomar\(d=0 .\) Para resolver (2.7.6), es mejor para hacer uso del método de Newton. Dejamos
\[F(r)=(r+d) \exp [(g+B / p)(r+d)]-m\{1-\exp [-(B / m)(r+d)]\} \nonumber \]
y diferenciarse con respecto\(r\) a obtener
\[F^{\prime}(r)=[1+(g+B / p)(r+d)] \exp [(g+B / p)(r+d)]-\frac{B}{m} \exp [-(B / m)(r+d)] . \nonumber \]
Para un dado\(B\), luego resolvemos\(F(r)=0\) iterando
\[r_{n+1}=r_{n}-\frac{F\left(r_{n}\right)}{F^{\prime}\left(r_{n}\right)} \nonumber \]
Usando valores de inicio apropiados para\(r\), la función\(r=r(B)\) puede ser calculada y se presenta en la Fig. 2.6. Evidentemente,\(r\) es máximo cerca del valor\(B=152\), que es\(53 \%\) del valor experimental para\(B\) mostrado en la Tabla\(2.3 .\)
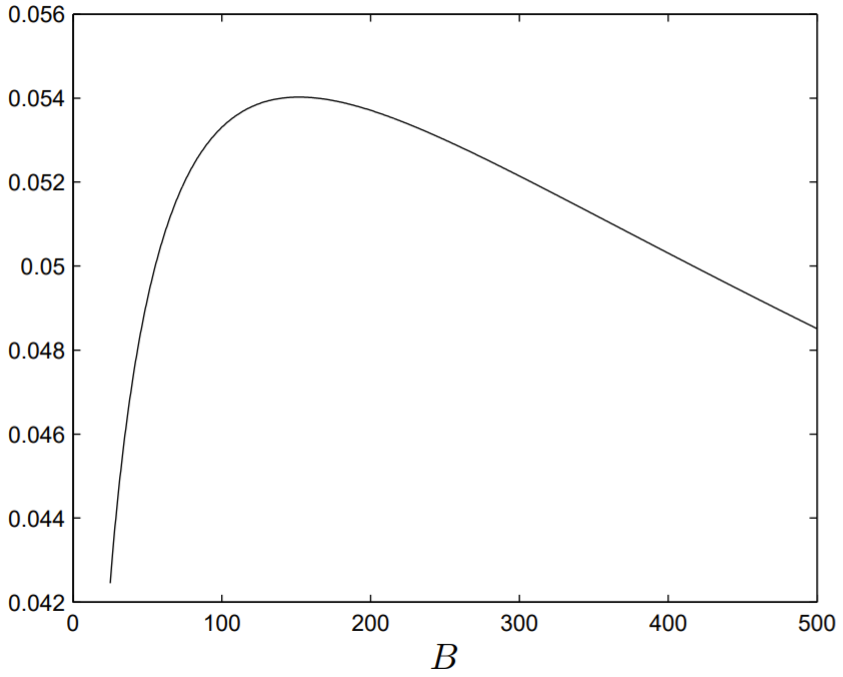
La ecuación (2.7.13) contiene los cuatro parámetros\(p, m, g\) y\(B\), que pueden reducirse aún más a tres parámetros mediante análisis dimensional. El tamaño de la cría ya\(B\) es adimensional. La velocidad\(m\) a la que se producen y ponen los óvulos se puede multiplicar por el período de producción de esperma\(s=B / p\) para formar el parámetro adimensional\(x=m B / p\). El parámetro\(x\) representa el número de óvulos olvidados debido al período de producción de esperma adulto y es una medida del costo de producción de esperma. De igual manera, se\(m\) puede multiplicar por el periodo de crecimiento larvario\(g\) para formar el parámetro adimensional\(y=m g\). El parámetro\(y\) representa el número de óvulos olvidados por el periodo de crecimiento juvenil y es una medida del costo de desarrollo. Con\(B, x\) y\(y\) como nuestros tres parámetros adimensionales,\((2.7.13)\) se convierte
\[\frac{1}{B}\left(1+\frac{B}{x}\right)^{\frac{x+y}{B}} \ln \left(1+\frac{B}{x}\right)=\frac{B}{B+x} . \nonumber \]
Dados valores para dos de los tres parámetros adimensionales\(x, y\) y\(B,(2.7.14)\) pueden resolverse para el parámetro restante, ya sea explícitamente para el caso de\(y=y(x, B)\), o por el método de Newton.
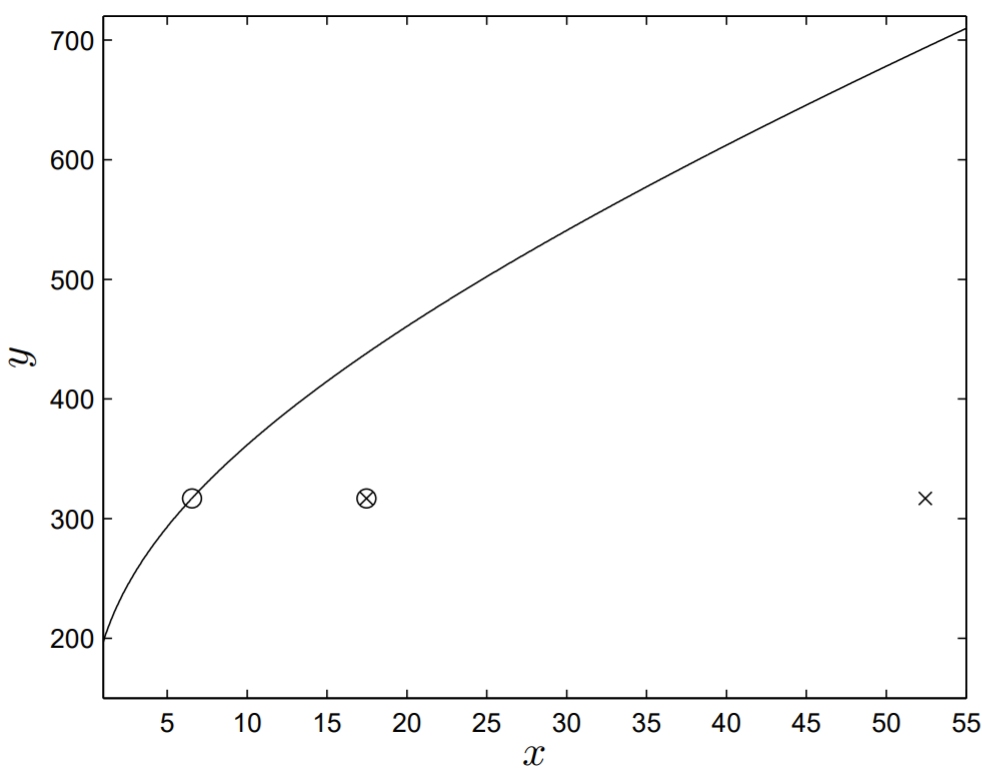
Los valores de\(x\) y\(y\) obtenidos de la Tabla\(2.3\) son\(x=52.5\) y\(y=317\). Con\(B=286\), la solución\(y=y(x)\) se muestra en la Fig. \(2.7\), con el valor experimental de\((x, y)\) trazado como un cruce.
El desacuerdo aparentemente grande entre el resultado teórico y los datos experimentales nos lleva a cuestionar los supuestos subyacentes del modelo. En efecto, Cutter (2004) sugirió por primera vez que el esperma producido de manera precoz como juvenil no retrasa la producción de óvulos y debe considerarse libre de costos. Una posibilidad es fijar el número absoluto de espermatozoides producidos de forma precoz y optimizar el número de espermatozoides producidos como adulto. Otra posibilidad es fijar la fracción de esperma producida de manera precoz y optimizar el número total de espermatozoides producidos. Esta última suposición la realizó Cutter (2004) y parece mejorar mejor la concordancia del modelo con los datos experimentales.
Por lo tanto, dividimos el periodo total de producción espermática\(s\) en juveniles y adultos
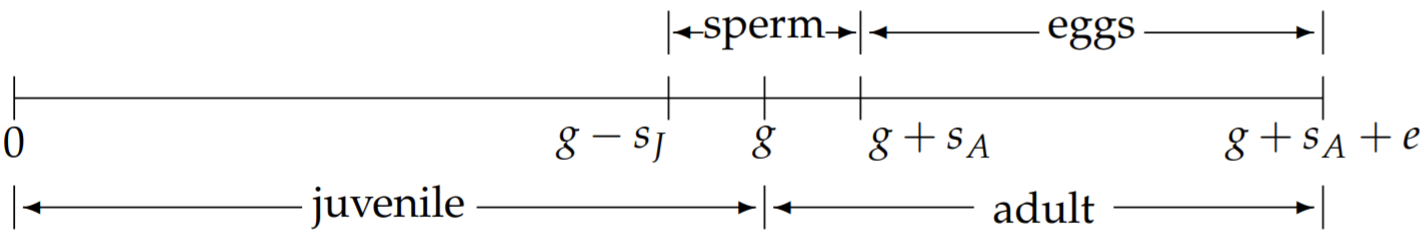
periodos de producción espermática\(s_{J}\) y\(s_{A}\), con\(s=s_{j}+s_{A} .\) La línea de tiempo revisada de la vida del hermafrodita ahora se muestra en la Fig. 2.8. Con la fracción de esperma producida como adulto denotada por\(f\), y la fracción producida como juvenil por\(1-f\), tenemos
\[s_{J}=(1-f) s, \quad s_{A}=f s . \nonumber \]
La ecuación (2.7.4) para la función de maternidad específica por edad se convierte
\[m(a)= \begin{cases}m & \text { for } g+s_{A}<a<g+s_{A}+e \\[4pt] 0 & \text { otherwise }\end{cases} \nonumber \]
con
\[s_{A}=f B / p . \nonumber \]
La ecuación de Euler-Lotka\((2.7.5)\) se cambia luego por la sustitución\(p \rightarrow p / f .\) Tras esta sustitución al resultado final dado por\((2.7.14)\) muestra que esta ecuación aún se mantiene (que de hecho es equivalente a (12) de Chasnov (2011)), pero con el ahora cambiado definición
\[x=m f B / p \nonumber \]
Un examen minucioso de los resultados mostrados en la Fig. \(2.7\)demuestra que se puede hacer un acuerdo casi perfecto entre los resultados del modelo teórico y los datos experimentales if\(f=1 / 8\) (mostrados como el círculo abierto en la Fig. 2.7). Cutter (2004) sugirió el valor de\(f=1 / 3\), y este resultado se muestra como un círculo abierto cruzado en la Fig. 2.7, aún en mucho mejor acuerdo con los datos experimentales que el círculo abierto correspondiente a\(f=1\). El modelado agregado de la producción precoz de esperma a través\(f\) del parámetro parece mejorar la verosimilitud del modelo con la biología subyacente.