6.2: Cinética enzimática

Las enzimas son catalizadores, generalmente proteínas, que ayudan a convertir otras moléculas llamadas sustratos en productos, pero a su vez no se modifican por la reacción. Cada enzima tiene alta especificidad para al menos una reacción, y puede acelerar esta reacción millones de veces. Sin enzimas, la mayoría de las reacciones bioquímicas son demasiado lentas para que la vida sea posible. Las enzimas son tan importantes para nuestras vidas que una mutación de un solo aminoácido en una enzima de las más de 2000 enzimas en nuestro cuerpo puede resultar en una enfermedad genética grave o letal.

Figura 6.1: Una reacción de Michaelis-Menten de dos sustratos que se convierten en un producto. (Dibujado por el usuario:IMEOWBOT, publicado bajo la Licencia de Documentación Libre de GNU.)

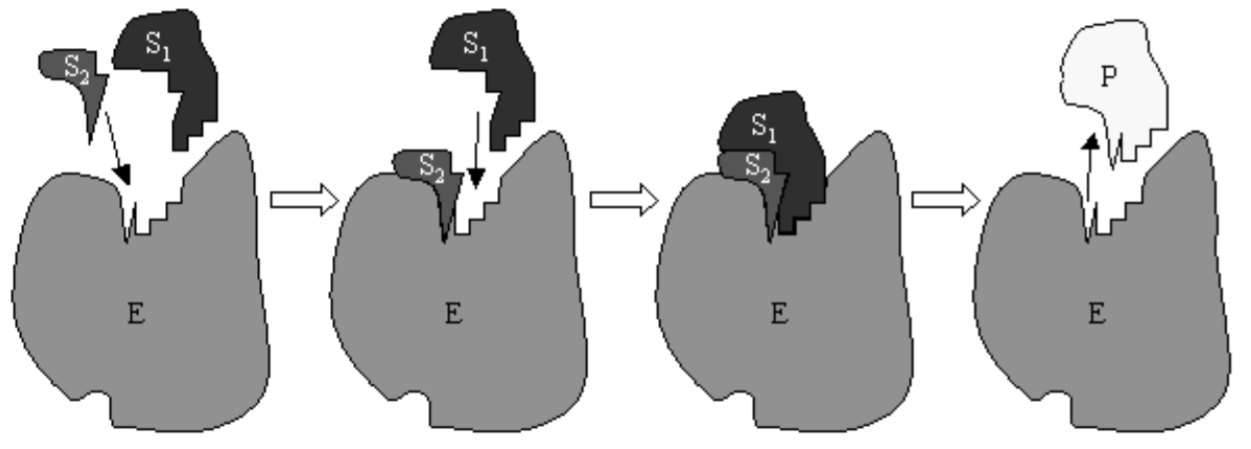
donde$C$ es un complejo formado por la enzima y el sustrato. En la Fig. 6.1 se muestra una caricatura de la reacción de Michaelis-Menten con una enzima que cataliza una reacción entre dos sustratos. Comúnmente, el sustrato se proporciona continuamente a la reacción y el producto se elimina continuamente. La eliminación del producto ha sido modelada al descuidar la reacción inversa$P+E \rightarrow C$. Una provisión continua de sustrato nos permite suponer que$S$ se mantiene a una concentración aproximadamente constante.

Las ecuaciones diferenciales para$C$ y se$P$ pueden obtener de la ley de acción de masas:

$$\begin{aligned} &d C / d t=k_{1} S E-\left(k_{-1}+k_{2}\right) C \\[4pt] &d P / d t=k_{2} C . \end{aligned} \nonumber$$

Los bioquímicos suelen querer determinar la velocidad de reacción$d P / d t$ en términos de la concentración de sustrato$S$ y la concentración total de enzimas$E_{0}$. Podemos eliminar$E$ a favor$E_{0}$ de la ley de conservación que se conserve la enzima, libre y unida; es decir

$$\frac{d(E+C)}{d t}=0 \quad \Longrightarrow \quad E+C=E_{0} \quad \Longrightarrow \quad E=E_{0}-C \nonumber$$

y podemos reescribir la ecuación para$d C / d t$ eliminar$E$:

$$\begin{align} \nonumber \frac{d C}{d t} &=k_{1} S\left(E_{0}-C\right)-\left(k_{-1}+k_{2}\right) C \\[4pt] &=k_{1} E_{0} S-\left(k_{-1}+k_{2}+k_{1} S\right) C \end{align} \nonumber$$

Debido a que$S$ se supone que se mantiene constante,$C$ se espera que el complejo esté en equilibrio, con la tasa de formación igual a la tasa de disociación. Con esta llamada aproximación cuasi-estable, podemos suponer que$C=0$ en$(6.3.4)$, y tenemos

$$C=\frac{k_{1} E_{0} S}{k_{-1}+k_{2}+k_{1} S} \nonumber$$

La velocidad de reacción viene dada por

$$\begin{align} \nonumber \frac{d P}{d t} &=k_{2} C \\[4pt] \nonumber &=\frac{k_{1} k_{2} E_{0} S}{k_{-1}+k_{2}+k_{1} S} \\[4pt] &=\frac{V_{m} S}{K_{m}+S} \end{align} \nonumber$$

donde se definen dos constantes fundamentales:

$$K_{m}=\left(k_{-1}+k_{2}\right) / k_{1}, \quad V_{m}=k_{2} E_{0} . \nonumber$$

La constante Michaelis-Menten o la constante Michaelis$K_{m}$ tiene unidades de concentración, y la velocidad máxima de reacción$V_{m}$ tiene unidades de concentración divididas por el tiempo. La interpretación de estas constantes se obtiene considerando los siguientes límites:

$$\begin{array}{ll} \text { as } S \rightarrow \infty, & C \rightarrow E_{0} \text { and } d P / d t \rightarrow V_{m} \\[4pt] \text { if } S=K_{m}, & C=\frac{1}{2} E_{0} \text { and } d P / d t=\frac{1}{2} V_{m} . \end{array} \nonumber$$

Por lo tanto,$V_{m}$ es la velocidad de reacción limitante obtenida saturando la reacción con sustrato de manera que cada enzima se une; y$K_{m}$ es la concentración$S$ a la que solo la mitad de las enzimas están unidas y la reacción avanza a la mitad velocidad máxima.