2.6: Tareas
- Page ID
- 113195
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Envíe la tarea por separado de este libro de trabajo y grapa todas las páginas juntas. (Un elemento básico para la presentación completa de toda la tarea de la unidad)
- Inicie un nuevo módulo en la parte frontal de una nueva página y escriba el número de módulo en la parte superior central de la página.
- Las respuestas sin apoyar el trabajo no recibirán crédito.
- Algunas soluciones se dan en el manual de soluciones.
- Puedes trabajar con compañeros de clase pero hacer tu propio trabajo.
Por cada dos conjuntos anotados, indique si los conjuntos coinciden o no. Si lo hacen, mostrar una coincidencia. Si no lo hacen, explique por qué no.
a. Pequeños bloques A azules y grandes bloques A rojos
b. bloques A amarillos y bloques A circulares
Describir una coincidencia entre el conjunto de números de conteo, {1, 2, 3,...} y el conjunto de múltiplos positivos de cinco, {5, 10, 15,...}.
Muestra cada correspondencia uno a uno posible entre los bloques A pequeños azules y los pequeños bloques A rojos. Usa abreviaturas o imágenes para denotar los bloques.
Convierte cada numeral a un numeral Hindu-Árabe Base Diez.
| a. apoplejía: | | | | | | | | | | | | | | | |
| b. Contador:\(\cancel{||||}\cancel{||||}\cancel{||||} |||\) |
| c. Romano: MCMLXII |
| d. romano: DCCXLIV |
| e. romano:\(\bar{\bar{\text{IV}}\text{CCX}}\) DLI |
|
f. Egipcio:  |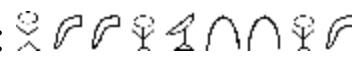
|
g. chino  |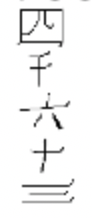
|
h. Maya  |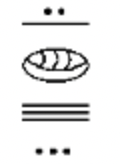
| i.\(4032_{\text{seven}}\) |
| j.\(T6W_{\text{thirteen}}\) |
| k.\(1 \ 111 \ 001 \ 011_{\text{two}}\) |
| l.\(507_{\text{nine}}\) |
Convierte 342 a un numeral en el sistema de numeración o base especificada.
| a. romano | b. Base Siete | c. Egipcio |
| d. Base Dos | e. Chino |
Convertir 838 a:
| a. Base Doce | b. Base Ocho |
| c. Base Cinco | d. Maya |
Convertir 13,595 a Base Doce
Convertir 120,258 a Maya
Cuenta de 620 a 630 en Base Cinco
Indique el número que viene justo antes:
| a.\(173 \ 425 \ 760_{\text{eleven}}\) | b.\(2 \ 010 \ 212 \ 000_{\text{four}}\) |
Indique el número que viene justo después de:
| a.\(539100TE_{\text{twelve}}\) | b.\(3 \ 102 \ 313 \ 444_{\text{five}}\) |
Responde verdadero o falso. Si es falso, explique por qué
| a.\(2_{\text{four}} = 2\) | b.\(3_{\text{four}} = 3_{\text{twelve}}\) | c.\(10_{\text{twelve}} = 10_{\text{five}}\) |
Usando Base Tres bloques, tenías 7 pisos, 10 largos y 5 unidades. ¿Qué número representa esto en
| a. ¿Base Tres? | b. ¿Base Diez? |
Escribe cada número mostrado en notación expandida como un numeral en la base especificada.
| a.\(3 \times 7^{8} + 6 \times 7^{5} + 4 \times 7^{4}\) a Base Siete |
| b.\(1 \times 3^{10} + 2 \times 3^{9} + 2 \times 3^{3}\) a la Base Tres |
Escribe cada número en notación expandida:
| a.\(200 \ 050 \ 030 \ 000_{\text{nine}}\) |
| b.\(1 \ 000 \ 100 \ 001 \ 000_{\text{two}}\) |
Escribe cada número en forma expandida. Después, convierte cada numeral a un número mixto Base Diez con la fracción simplificada.
| a.\(43.3_{\text{nine}}\) | b.\(35.12_{\text{six}}\) |
| c.\(121.21_{\text{three}}\) | d.\(333.333_{\text{five}}\) |
Reescribe de forma expandida a un numeral en la base apropiada.
| a.\(3 \times 4^{2} + 2 \times 4^{0} + 3 \times 4^{-1} + 1 \times 4^{-3}\) |
| b.\(5 \times 11^{3} + 10 \times 11^{1} + 8 \times 11^{-1} + 1 \times 11^{-2}\) |
| c.\(1 \times 2^{2} + 1 x\times 2^{0} + 1 \times 2^{-1} + 1 \times 2^{-4}\) |