3.2: Combinando
- Page ID
- 113200
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Necesitarás: Bloques Base (Tarjetas de Material 4-15)
Comenzaremos este ejercicio establecido averiguando cómo agregar en el sistema numérico egipcio. Te recuerdan los símbolos y sus equivalentes hindu-árabes a continuación:
| | (1) |
 (10) |
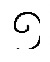 (100) |
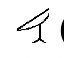 (1,000) |
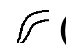 (10,000) |
 (100.000) |
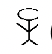 (1,000,000) |
Dado que el sistema de numeración egipcio es un sistema aditivo básico, la suma de dos números se forma simplemente combinando los símbolos de ambos números juntos. Debido a que es un sistema Base Diez, se puede realizar un intercambio cada vez que haya diez del mismo símbolo reemplazando diez de un símbolo por el siguiente símbolo superior. Para demostrar que se está realizando un intercambio, se puede dar un círculo, poner una caja alrededor o subrayar diez del mismo símbolo. En los ejemplos que siguen, los intercambios se indican poniendo una caja alrededor de un grupo de diez símbolos que van a ser reemplazados por un nuevo símbolo en el siguiente paso. Después de cada intercambio, puede ser necesario realizar otro intercambio. Estudie los siguientes ejemplos de problemas de adición egipcios. Intenta pensar en egipcio como haces esto simplemente siguiendo las reglas de combinar e intercambiar en lugar de pensar en qué números representa cada número en hindu-árabe. Después de trabajar en cada problema, siempre se puede volver atrás y verificar convirtiendo primero cada uno de los números que se están agregando (las adiciones) a hindu-árabe, sumarlos juntos y luego verificando que la suma concuerde con la respuesta obtenida en egipcio.
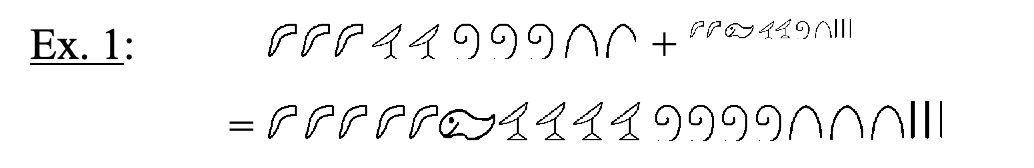 |
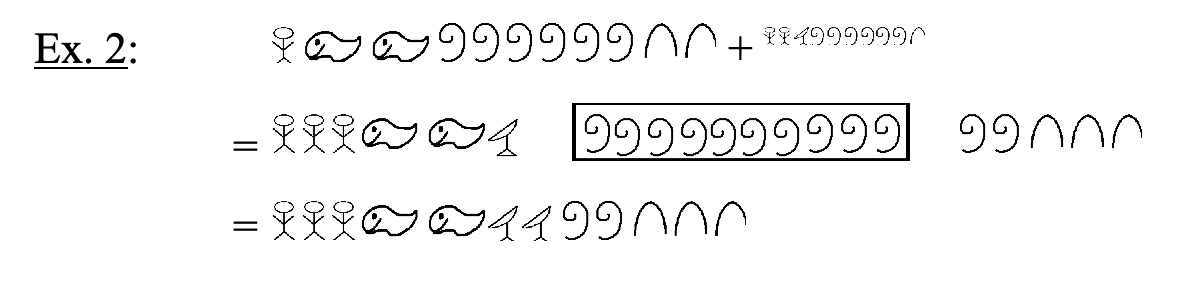 |
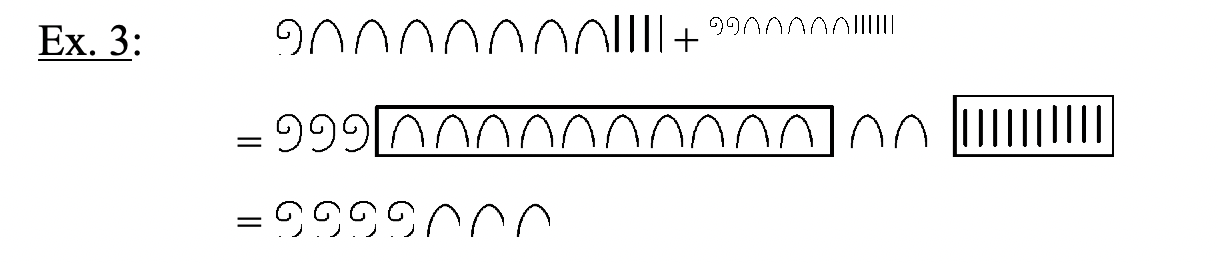 |
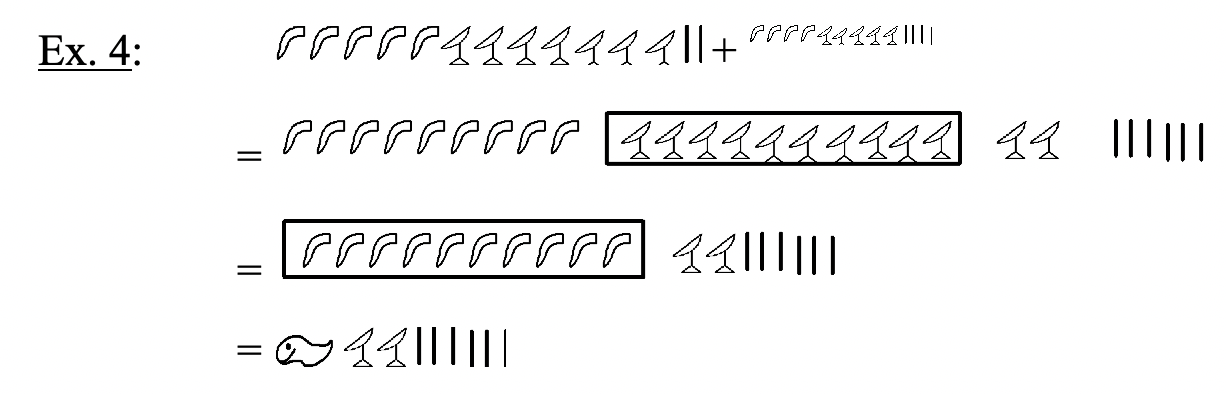 |
Añádese los siguientes números egipcios. Mostrar todos los pasos, indicando los cambios realizados. Nuevamente, trata de trabajar a través de estos pensando sólo en egipcio. Siempre puedes volver atrás y comprobar cuando termines haciéndolos en hindu-árabe. Informar tus propios problemas para la parte e y la parte f.
|
a. 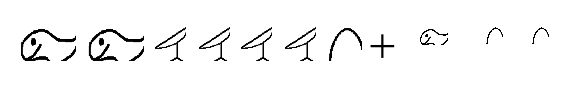 |
|
b. 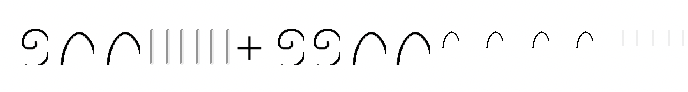 |
|
c. 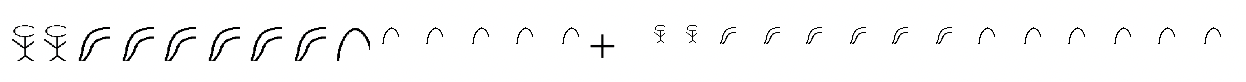 |
|
d. 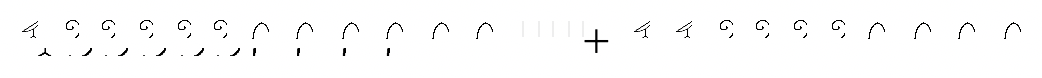 |
Pretendamos que nuestro sistema actual de dinero estaba estrictamente en Base Diez para que la única moneda que usábamos fueran centavos, diez centavos, billetes de un dólar, billetes de diez dólares, billetes de cien dólares, billetes de mil dólares y así sucesivamente. En lugar de dibujar dibujos del dinero, se utilizarán estas abreviaturas para cada tipo de moneda o billete: centavo (A), moneda de diez centavos (B), billete de un dólar (C), billete de diez dólares (D), billete de cien dólares (E), billete de mil dólares (F) y así sucesivamente. Dado que la mayoría de ustedes están considerando ingresar a la profesión docente, probablemente no necesitará manejar nada superior a un billete de mil dólares. Al menos ese es el caso ya que escribo esto en 1999 pero quién sabe lo que depara el futuro, ¿verdad?
Mostrar qué intercambios se podrían realizar para cada uno de los siguientes:
| a. AAAAAAAAAA = ____ | b. CCCCCCCCCC = ____ | c. FFFFFFFFFF = ____ |
Formar cada suma combinando los dos agregados en un solo bulto. Realizar los intercambios según sea necesario para que la suma esté representada por el menor número de monedas o billetes. Mostrar todos los pasos, indicando los cambios realizados.
| a. CCAADDDCB + BBBBBBBBBAAACC |
| b. AAAACCCCCCCCCEEE + CCCCBBA |
| c. EEEEEEEEAAAAAAAA + EEEAA |
| d. DDDDCCCCCBBBBB + DDDDDDCCCCBBBBB |
Para sumar en el sistema maya, el primer paso es combinar los símbolos de cada nivel juntos. Los símbolos de cada nivel deben combinarse por separado. Entonces, en cada nivel, mira para ver si se puede hacer algún intercambio. Un grupo de cinco puntos siempre se puede intercambiar por un segmento de línea. Los intercambios de un nivel a otro son un poco más complejos. Un grupo de 20 en un nivel puede negociarse por un punto en el siguiente nivel arriba excepto del segundo al tercer nivel donde un grupo de 18 en el segundo nivel puede negociarse por un punto en el tercer nivel. Estudie los siguientes ejemplos de números mayas de un nivel que se suman. Cada vez que se realiza un intercambio, se pondrá un círculo o caja alrededor de lo que se reemplazará en el siguiente paso. Se utilizará una flecha para indicar si se está realizando un intercambio de un nivel al siguiente nivel arriba. La flecha indica que un punto estará en el siguiente nivel arriba en el siguiente paso en lugar de la cantidad encajada en el nivel original. Ver ejemplo 2 a continuación: Del paso 2 al paso 3, los cuatro segmentos de línea en el nivel uno son reemplazados por un punto en el nivel dos.
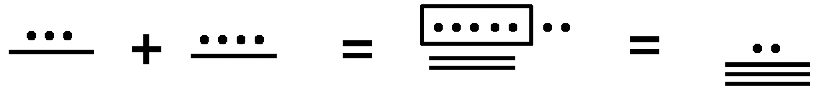
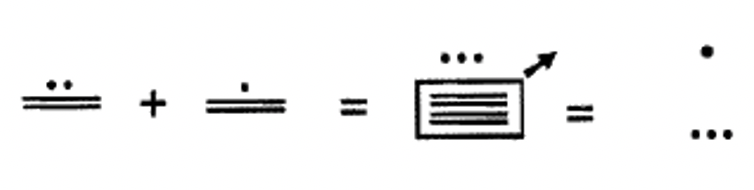

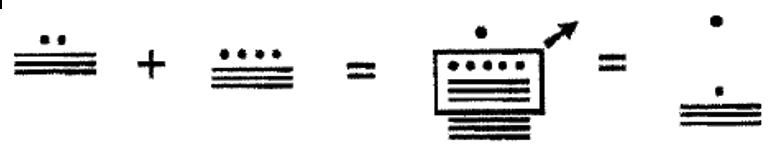
Sumar los siguientes números mayas de un solo nivel juntos. Realiza los intercambios necesarios y muestra todos los pasos.
|
a. 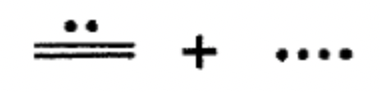 |
|
b. 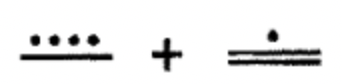 |
|
c. 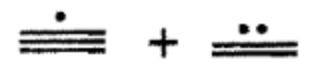 |
Estudie los siguientes ejemplos en esta y la siguiente página de sumar números mayas juntos. Todos estos son más de un nivel. Se utilizan espacios amplios para diferenciar entre los diferentes niveles. Intenta hacerlas tú mismo en tu propio papel.
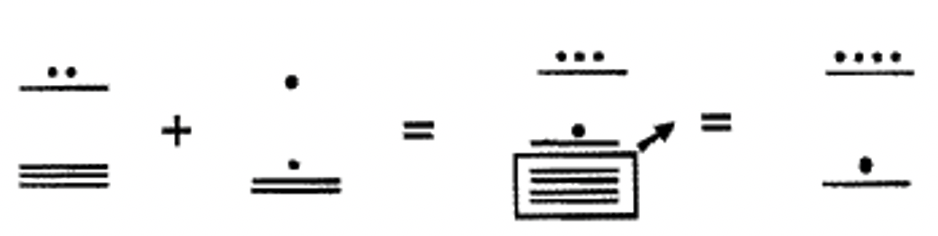


Recuerda, ¡un grupo de 18 en el segundo nivel se puede cambiar por un punto en el tercer nivel!
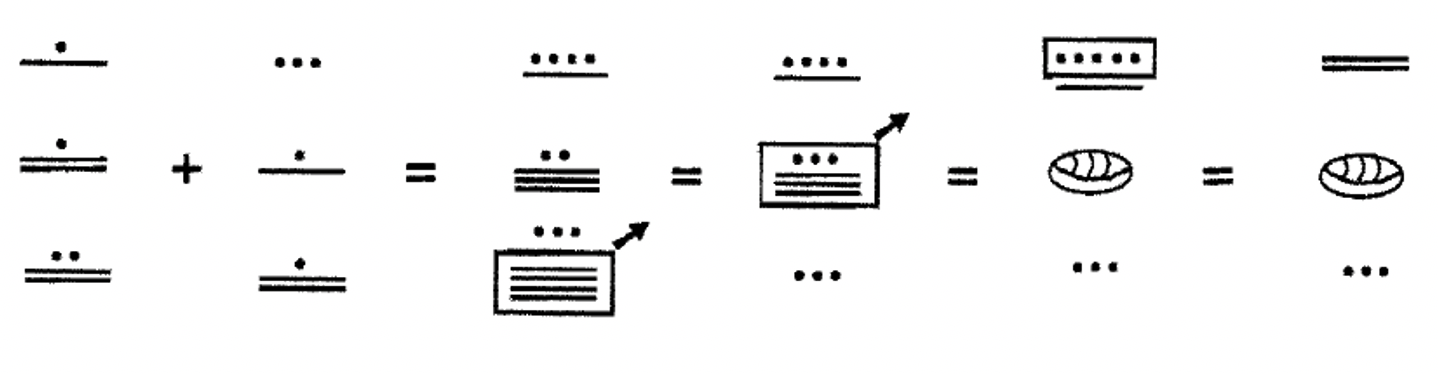
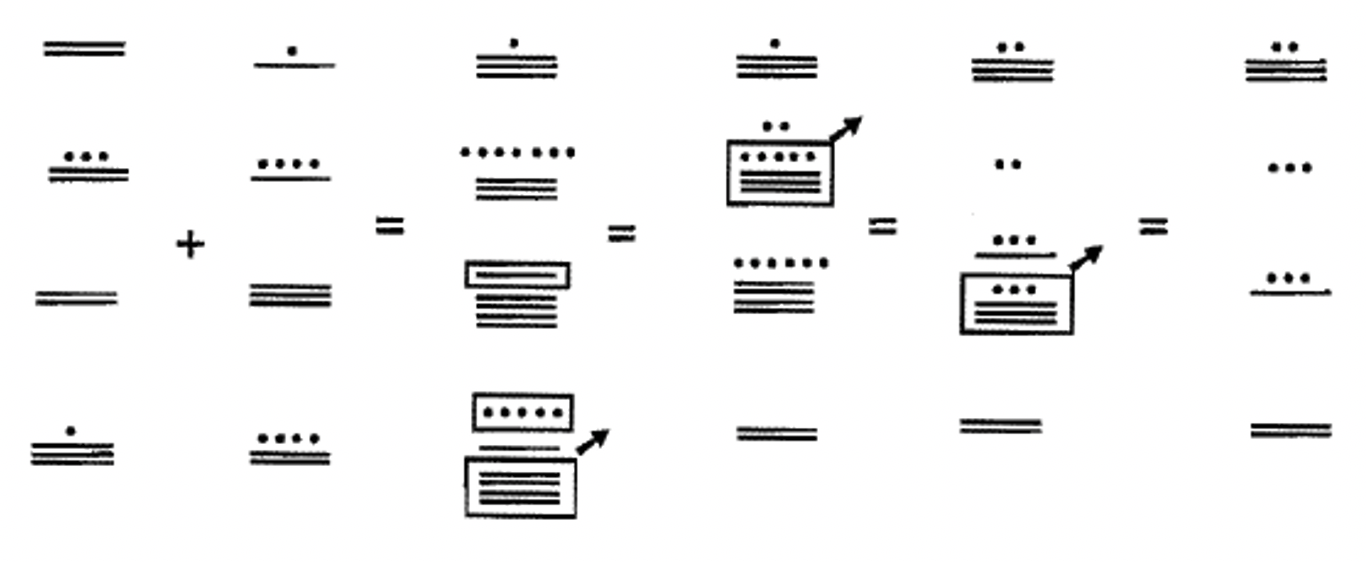
Después de hacer cada uno de los ejemplos anteriores únicamente en maya, verifiqué cada problema convirtiendo cada adenda al hindu-árabe, agregando en Base Diez, convirtiendo la suma en maya y asegurándose de que la respuesta coincidiera con la respuesta que había obtenido. Cuando comprobé el Ejemplo 5 (76,896 + 46,754 = 123,650), un problema bastante complicado, no se comprobó. Entonces rediseñé el problema hasta que lo hice bien. Es una buena idea revisar cuidadosamente tu trabajo a medida que avanzas lo cual requiere fuertes dosis de concentración, esfuerzo y paciencia. De lo contrario, es bastante fácil cometer uno o más errores durante el cómputo. Ten en cuenta que si todo lo que haces es convertir al Hindu-Árabe, agregar y volver a convertir al maya, no obtendrás crédito porque eso no mostraría todos los pasos involucrados, combinar, intercambiar, etc. que debes mostrar cuando haces los ejercicios. Pruebe cada uno de los ejemplos anteriores en una hoja de papel separada para asegurarse de que los está trabajando correctamente. Tenga en cuenta que la secuencia de pasos que se muestra para cada ejemplo podría no ser la única forma de llegar a la respuesta correcta.
Sumar los siguientes números mayas juntos. Realiza los intercambios necesarios y muestra todos los pasos. Es una muy buena idea revisar tu trabajo y eso no significa buscar la respuesta en las soluciones! Después de agregar en maya, convertir la respuesta a hindu-árabe. Después, convierte los dos números originales a Hindu-Árabe y sumar y ver si coincide con la respuesta.
|
a. 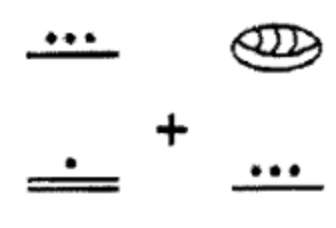 |
|
b. 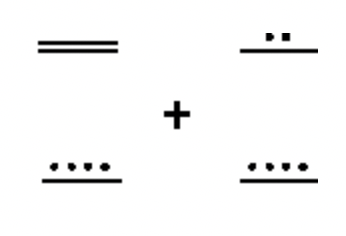 |
|
c. 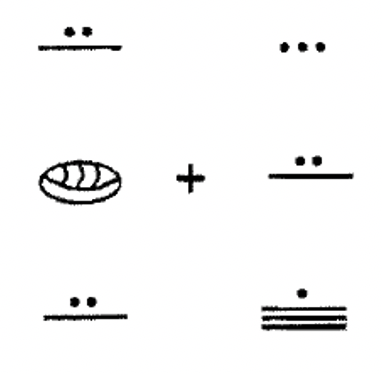 |
|
d. 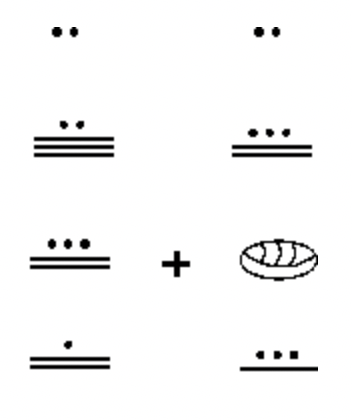 |
|
e.  |
Cuenta 15 bloques unitarios y realiza intercambios con base cuatro bloques. Ponlos en una pila, llamada Pila A, y GUARDA ESTA PILA. Ya que has realizado intercambios en la base cuatro, escribe 15 como un número base cuatro en el espacio proporcionado para la Pila A a continuación. Ahora, cuente 13 unidades más y realice intercambios con base cuatro bloques. Póngalos en una pila, llamada Pila B. Ya que has realizado intercambios en la base cuatro, escribe 13 como un numeral base cuatro en el espacio provisto para el Pila B a continuación. Para agregar, simplemente combina los bloques de la Pila A y la Pila B para formar una gran pila de bloques. ¡Estás formando la unión de Pila A y Pila B! Haga todos los intercambios posibles con bloques base cuatro y luego escriba el número de unidades en la pila combinada como un numeral base cuatro en el espacio provisto.
Combinar las dos pilas es lo mismo que formar la suma de los dos números. Acabas de sumar dos números juntos en una base diferente.
A continuación se muestra el problema de adición que acaba de realizar en Base Cuatro.
____________ + _____________ = ____________
Pila A Pila B Pila Combinada
Cuenta 15 bloques unitarios y realiza intercambios con base siete bloques. Ponlos en una pila, llamada Pila A, y GUARDA ESTA PILA. Ya que has realizado intercambios en base siete, escribe 15 como un número base siete en el espacio provisto para la Pila A a continuación. Ahora, cuente 13 unidades más y realice intercambios con base siete bloques. Póngalos en una pila, llamada Pila B. Ya que has realizado intercambios en base siete, escribe 13 como un número base siete en el espacio provisto para la Pila B a continuación. Para agregar, simplemente combina los bloques de la Pila A y la Pila B para formar una gran pila de bloques. ¡Estás formando la unión de Pila A y Pila B! Haga todos los intercambios posibles con bloques base siete y luego escriba el número de unidades en la pila combinada como un número base siete en el espacio que se proporciona a continuación.
Combinar las dos pilas es lo mismo que formar la suma de los dos números. Acabas de sumar dos números juntos en una base diferente.
A continuación se muestra el problema de adición que acaba de realizar en Base Siete
____________ + _____________ = ____________
Pila A Pila B Pila Combinada
Cuenta 15 bloques unitarios y realiza intercambios con base de dos bloques. Ponlos en una pila, llamada Pila A, y GUARDA ESTA PILA. Ya que has realizado intercambios en la base dos, escribe 15 como un número base dos en el espacio proporcionado para la Pila A a continuación. Ahora, cuente 13 unidades más y realice intercambios con base de dos bloques. Póngalos en una pila, llamada Pila B. Ya que has realizado intercambios en la base dos, escribe 13 como un número base dos en el espacio provisto para la Pila B a continuación. Para agregar, simplemente combina los bloques de la Pila A y la Pila B para formar una gran pila de bloques. ¡Estás formando la unión de Pila A y Pila B! Haga todos los intercambios posibles con bloques base dos y luego escriba el número de unidades en la pila combinada como un numeral base dos en el espacio provisto.
Combinar las dos pilas es lo mismo que formar la suma de los dos números. Acabas de sumar dos números juntos en una base diferente.
A continuación se muestra el problema de adición que acaba de realizar en Base Dos.
____________ + _____________ = ____________
Pila A Pila B Pila Combinada
Cuenta 15 bloques unitarios y realiza intercambios con base nueve bloques. Ponlos en una pila, llamada Pila A, y GUARDA ESTA PILA. Ya que has realizado intercambios en base nueve, escribe 15 como un número base nueve en el espacio proporcionado para la Pila A a continuación. Ahora, cuente 13 unidades más y realice intercambios con bloques base nueve. Ponlos en una pila, llamada Pila B. Ya que has realizado intercambios en la base nueve, escribe 13 como un numeral base nueve en el espacio provisto para la Pila B a continuación. Para agregar, simplemente combina los bloques de la Pila A y la Pila B para formar una gran pila de bloques. ¡Estás formando la unión de Pila A y Pila B! Haga todos los intercambios posibles con bloques base nueve y luego escriba el número de unidades en la pila combinada como un número base nueve en el espacio provisto.
Combinar las dos pilas es lo mismo que formar la suma de los dos números. Acabas de sumar dos números juntos en una base diferente.
A continuación se muestra el problema de adición que acaba de realizar en Base Nueve.
____________ + _____________ = ____________
Pila A Pila B Pila Combinada
Cuenta 15 bloques unitarios y realiza intercambios con base de tres bloques. Ponlos en una pila, llamada Pila A, y GUARDA ESTA PILA. Ya que has realizado intercambios en la base tres, escribe 15 como un número base tres en el espacio proporcionado para la Pila A a continuación. Ahora, cuente 13 unidades más y realice intercambios con base de tres bloques. Póngalos en una pila, llamada Pila B. Ya que has realizado intercambios en la base tres, escribe 13 como un numeral base tres en el espacio provisto para la Pila B a continuación. Para agregar, simplemente combina los bloques de la Pila A y la Pila B para formar una gran pila de bloques. ¡Estás formando la unión de Pila A y Pila B! Haga todos los intercambios posibles con bloques base tres y luego escriba el número de unidades en la pila combinada como un numeral base tres en el espacio que se proporciona a continuación.
Combinar las dos pilas es lo mismo que formar la suma de los dos números. Acabas de sumar dos números juntos en una base diferente.
A continuación se muestra el problema de adición que acaba de realizar en Base Tres
____________ + _____________ = ____________
Pila A Pila B Pila Combinada
Cuenta 15 bloques unitarios y realiza intercambios con ocho bloques base. Ponlos en una pila, llamada Pila A, y GUARDA ESTA PILA. Ya que has realizado intercambios en la base ocho, escribe 15 como un número base ocho en el espacio proporcionado para la Pila A a continuación. Ahora, cuente 13 unidades más y realice intercambios con bloques base ocho. Póngalos en una pila, llamada Pila B. Ya que has realizado intercambios en base ocho, escribe 13 como un numeral base ocho en el espacio provisto para el Pila B a continuación. Para agregar, simplemente combina los bloques de la Pila A y la Pila B para formar una gran pila de bloques. ¡Estás formando la unión de Pila A y Pila B! Haga todos los intercambios posibles con bloques base ocho y luego escriba el número de unidades en la pila combinada como un numeral base ocho en el espacio que se proporciona a continuación.
Combinar las dos pilas es lo mismo que formar la suma de los dos números. Acabas de sumar dos números juntos en una base diferente.
A continuación se muestra el problema de adición que acaba de realizar en Base Ocho.
____________ + _____________ = ____________
Pila A Pila B Pila Combinada
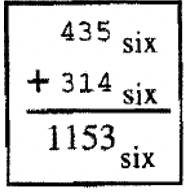
Escribe los seis problemas de suma de los ejercicios 6-11 en un formato vertical como el de Base Seis que se muestra a continuación. Estudie este problema de Base Seis así como los seis problemas de los seis ejercicios anteriores. Trate de encontrar una manera de hacer los problemas de adición usando papel y lápiz en lugar de usar los Bloques Base. En otras palabras, trata de idear tu propio algoritmo (método) para hacer suma en otras bases. Explica tu método y muestra algunos ejemplos. En el siguiente Conjunto de ejercicios, estarás aprendiendo algoritmos para sumar.
Vamos m < b y n < b. definamos la palabra “complemento” de un número,\(m_{b}\), en una base dada b para que sea el número,\(n_{b}\), tal\(m_{b} + n_{b} = 10_{b}\). (No lea 10b como “diez, base b”). En otras palabras, piense en mb como un número de unidades individuales menor que la base, b. Entonces el complemento, n b, sería el número de unidades individuales que se necesita para sumar a m b de tal manera que la suma de m b y n b podría ser negociado por exactamente un largo. Nota: ¡Complemento como se define aquí no tiene nada que ver con la palabra complemento como la definimos y la usamos en Teoría de Conjuntos! Los ejemplos de la página siguiente deberían aclarar esta definición.
A continuación se presentan algunos ejemplos de complementos. Se debe especificar la base.
En Base Diez: 3 y 7 son complementos ya que 3 + 7 = 10
4 y 6 son complementos ya que 4 + 6 = 10
8 es el complemento de 2 ya que 8 + 2 = 10
5 es el complemento de 5 desde 5 + 5 = 10
En Base Ocho: el complemento de\(5_{\text{eight}}\) es 3\(_{\text{eight}}\) ya que 5\(_{\text{eight}}\) + 3\(_{\text{eight}}\) = 10\(_{\text{eight}}\)
4\(_{\text{eight}}\) y 4\(_{\text{eight}}\) son complementos ya que 4\(_{\text{eight}}\) + 4\(_{\text{eight}}\) = 10\(_{\text{eight}}\)
2\(_{\text{eight}}\) y 6\(_{\text{eight}}\) son complementos ya que 2\(_{\text{eight}}\) + 6\(_{\text{eight}}\) = 10\(_{\text{eight}}\)
7\(_{\text{eight}}\) es el complemento de 1\(_{\text{eight}}\) ya que 7\(_{\text{eight}}\) + 1\(_{\text{eight}}\) = 10\(_{\text{eight}}\)
Escribe el complemento de cada número:
| a.\(7_{\text{nine}}\) | b.\(5_{\text{seven}}\) | c.\(2_{\text{tweleve}}\) |
| d.\(3_{\text{eleven}}\) | e.\(2_{\text{six}}\) | f.\(1_{\text{two}}\) |
| g.\(2_{\text{three}}\) | h.\(1_{\text{four}}\) | i.\(3_{\text{five}}\) |
Aunque no necesariamente un esfuerzo consciente, muchas personas utilizan complementos y la propiedad asociativa de adición para agregar. Por ejemplo, algunas personas utilizan la siguiente estrategia para agregar en Base Diez. Digamos que el problema era sumar 8 y 6. Una persona podría pensar “tengo 8 y solo se necesitan 2 más para llegar a 10. Si tomo 2 del 6 y lo agrego al 8, entonces tengo 10 + 4 que es 14" En otras palabras, el problema 8 + 6 se convierte en 8 + (2 + 4) = (8 + 2) + 4 = 10 + 4 = 14. Por supuesto, lo hacen de manera más automática de lo que parece cuando está escrito.
El mismo tipo de estrategia se puede utilizar en otras bases. Estudia los siguientes ejemplos. Podría ser útil si usas unidades y largos en los Bloques Base.
\(4_{\text{nine}} + 8_{\text{nine}} = 4_{\text{nine}} + (5_{\text{nine}} + 3_{\text{nine}}\))
= (\(4_{\text{nine}} + 5_{\text{nine}}) + 3_{\text{nine}}\)
=\(10_{\text{nine}} + 3_{\text{nine}}\)
=\(13_{\text{nine}}\) (que es 1 largo y 3 unidades en base nueve)
\(T_{\text{twelve}} + 9_{\text{twelve}} = T_{\text{twelve}} + (2_{\text{twelve}} + 7_{\text{twelve}}\))
= (\(T_{\text{twelve}} + 2_{\text{twelve}}) + 7_{\text{twelve}}\)
=\(10_{\text{twelve}} + 7_{\text{twelve}}\)
=\(17_{\text{twelve}}\) (que es 1 largo y 7 unidades en base doce)
\(4_{\text{six}} + 4_{\text{six}} = 4_{\text{six}} + (2_{\text{six}} + 2_{\text{six}}\))
= (\(4_{\text{six}} + 2_{\text{six}}) + 2_{\text{six}}\)
=\(10_{\text{six}} + 2_{\text{six}}\)
=\(12_{\text{six}}\) (que es 1 largo y 2 unidades en base seis)
Usa tus Bloques Base o la definición de complementos para hacer los siguientes problemas de adición:
| a.\(7_{\text{eleven}} + 8_{\text{eleven}}\) | b.\(4_{\text{five}} + 3_{\text{five}}\) |
| c.\(2_{\text{eight}} + 7_{\text{eight}}\) | d.\(9_{\text{thirteen}} + 5_{\text{thirteen}}\) |
| e.\(3_{\text{four}} + 3_{\text{four}}\) | f.\(6_{\text{seven}} + 4_{\text{seven}}\) |
| g.\(2_{\text{three}} + 2_{\text{three}}\) = | h.\(1_{\text{two}} + 1_{\text{two}}\) |
| i.\(3_{\text{six}} + 5_{\text{six}}\) | j.\(7_{\text{nine}} + 5_{\text{nine}}\) |
Ahora que puedes sumar números de un solo dígito en cualquier base, puedes componer tablas de suma. A continuación se presentan tablas de suma en Base Cinco y Base Ocho. Dado que la Base Cinco tiene cinco dígitos, su tabla de adiciones debe ser una cuadrícula de cinco por cinco y dado que la Base Ocho tiene ocho dígitos, su tabla de adiciones debe ser una cuadrícula de ocho por ocho. Observe cómo la simetría, la propiedad conmutativa y la propiedad que x + 0 = x para todos x hace que gran parte de la tabla sea fácil de rellenar. Al hacer tablas de suma (y posteriormente al hacer tablas de multiplicar) en diferentes bases, debes etiquetar qué tipo de tabla es. Si haces eso, entonces la convención será que no es necesario escribir la palabra para qué base está a la derecha de cada numeral.
Tabla\(\PageIndex{1}\): Tabla de Adición Base Cinco
| + | 0 | 1 | 2 | 3 | 4 |
| 0 | 0 | 1 | 2 | 3 | 4 |
| 1 | 1 | 2 | 3 | 4 | 10 |
| 2 | 2 | 3 | 4 | 10 | 11 |
| 3 | 3 | 4 | 10 | 11 | 12 |
| 4 | 4 | 10 | 11 | 12 | 13 |
Mesa\(\PageIndex{2}\): Mesa de Adición Base Ocho
| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 |
| 3 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 12 |
| 4 | 4 | 5 | 6 | 7 | 10 | 11 | 12 | 13 |
| 5 | 5 | 6 | 7 | 10 | 11 | 12 | 13 | 14 |
| 6 | 6 | 7 | 10 | 11 | 12 | 13 | 14 | 15 |
| 7 | 7 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
Componen mesas de suma en la base especificada.
| a. Mesa de Adición Base Tres |
| b. Tabla de Adición Base Seis |
| c. Tabla de Adición Base Dos |


