9.2: Números racionales
- Page ID
- 113272
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Materiales: Círculos de fracción, Matrices de Fracciones, Tiras Múltiples, Tiras
Usa tus círculos de fracciones marcadas para realizar estas primeras actividades.
Toma una cuña de cada círculo de fracción (1/2, 1/3, 1/4, 1/5, 1/6, 1/8, 1/9, 1/10 y 1/12). Una fracción es mayor que otra si cubre más espacio que la otra fracción. Compárelos y ponlos en orden de menor a mayor, y escríbelos en orden a continuación, usando el símbolo menor que (<).
De lo que descubriste en el ejercicio 1, circule la fracción mayor en cada caso.
| a. 1/90 ó 1/95 | b. 1/32 ó 1/33 |
Si tomas 5 de las piezas de fracción que dicen 1/8, entonces juntas tienes 5/8. Usa este hecho para hacer el siguiente ejercicio.
Utilice los círculos de fracción para comparar 5/6, 5/8, 5/9, 5/10 y 5/12. Póngalos en orden de menor a mayor usando el símbolo menor que (<).
De lo que descubriste en el ejercicio 3, circule la fracción mayor en cada caso.
| a. 15/37 ó 15/40 | b. 89/100 ó 89/200 |
Utilice la matriz de fracciones para ordenar estas fracciones: 4/5, 4/6, 4/7, 4/8, 4/9, 4/10, 4/11 y 4/12. Póngalos en orden de menor a mayor usando el símbolo menor que (<).
Explica el patrón que aprendiste al hacer los ejercicios 1-5.
Utilice círculos de fracciones para comparar estas fracciones: 1/2, 2/3, 3/4, 4/5, 5/6, 7/8, 8/9, 9/10 y 11/12. Póngalos en orden de menor a mayor usando el símbolo menor que (<).
Utilice la matriz de fracciones para ordenar estas fracciones: 1/2, 2/3, 3/4, 4/5, 5/6, 7/8, 8/9, 9/10, 11/12. Póngalos en orden de menor a mayor usando el símbolo menor que (<).
De lo que descubriste en los ejercicios 7 y 8, circule la fracción mayor en cada caso.
| a. 89/90 ó 94/95 | b. 56/57 ó 31/33 |
Ordene estas fracciones: 45/46, 71/72, 34/35, 99/100, 25/26, 13/14, 51/52. Póngalos en orden de menor a mayor usando el símbolo menor que (<).
Explica el patrón que aprendiste al hacer ejercicios 7 - 10.
Dibuja un modelo propio que ayudaría a convencer a alguien de por qué 4/5 era mayor que 2/3.
Un número racional es simplemente el nombre formal de una fracción. A continuación se muestra una definición formal de un número racional.
Un número racional es un número que se puede escribir como el cociente (ratio) de un entero,\(m\), y un entero distinto de cero\(n\),, que se escribe así:\(\frac{m}{n}\).
Cuando se escribe en esta forma,\(m\) se llama numerador y\(n\) se llama denominador. Si GCF (\(m,n\)) = 1 (es decir,\(m\) y no\(n\) tienen factores en común), entonces se dice que el número racional está en forma más simple (o reducida).
La siguiente es una forma de representar un número racional,\(\frac{m}{n}\).
Divida una unidad (definida) en un número igual de\(n\) partes o subconjuntos. Lo que significa que\(n\) las partes componen un todo. Cada una de estas partes (o subconjuntos) representa\(\frac{1}{n}\). Entonces,\(m\) de esas partes representa\(\frac{m}{n}\).
Para cada número racional,\(\frac{m}{n}\),
- Definir una unidad en términos de puntos. Afirma el valor de cada punto.
- Divida la unidad en un número igual (el denominador) de partes.
- Mostrar una representación de\(\frac{1}{n}\).
- Mostrar una representación de\(\frac{m}{n}\).
- Defina la unidad de manera diferente, y vuelva a hacer las tres partes (i, ii y iii).
|
a. Deje que una unidad esté definida por 8 puntos, como se muestra a continuación. Cada punto = 1/8 \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] i. La unidad se divide en 8 partes iguales, como se muestra a continuación.  ii. A continuación se muestra una representación de 1/8, que es una de las partes iguales que se muestran en la parte b. \[\boldsymbol{\cdot}\nonumber \] III.A continuación se muestra una representación de 3/8. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
b. Que una unidad esté definida por 16 puntos, como se muestra a continuación. Cada punto = 1/16 \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] i. La unidad se divide en 8 partes iguales, como se muestra a continuación.  ii. A continuación se muestra una representación de 1/8, que es una de las partes iguales que se muestran en la parte b. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] III.A continuación se muestra una representación de 3/8. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Observe que hay 3 puntos para la respuesta en la parte a, donde cada punto representa 1/8. Entonces, los 3 puntos representan el número 3/8. Para la parte b, la respuesta tiene 6 puntos. Dado que cada punto representa 1/16, esto también representa 6/16. Por lo tanto, 3/8 y 6/16 deben representar el mismo número. Dos fracciones que representan el mismo número se denominan fracciones equivalentes.
Es crucial definir tu unidad antes de comenzar cualquier ejercicio!!
|
a. Deje que una unidad esté definida por 5 puntos, como se muestra a continuación. Cada punto = 1/5 \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] i. La unidad se divide en 5 partes iguales, como se muestra a continuación.  ii. A continuación se muestra una representación de 1/5, que es una de las partes iguales que se muestran en la parte b. \[ \boldsymbol{\cdot} \nonumber \] III.A continuación se muestra una representación de 2/5. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
b. Que una unidad esté definida por 10 puntos, como se muestra a continuación. Cada punto = 1/10 \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] i. La unidad se divide en 5 partes iguales, como se muestra a continuación.  ii. A continuación se muestra una representación de 1/5, que es una de las partes iguales que se muestran en la parte b. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] III.A continuación se muestra una representación de 2/5 \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Observe que hay 2 puntos para la respuesta en la parte a, donde cada punto representa 1/5. Entonces, los 2 puntos representan el número 2/5. Para la parte b, la respuesta tiene 4 puntos. Dado que cada punto representa 1/10, esto también representa 4/10. Por lo tanto, 2/5 y 4/10 deben representar el mismo número. Dos fracciones que representan el mismo número se denominan fracciones equivalentes.
ES CRUCIAL DEFINIR TU UNIDAD ANTES DE COMENZAR CUALQUIER
Utilice el método en los dos últimos ejemplos para mostrar dos representaciones diferentes para 3/4.
Utilice sus matrices de fracciones para determinar todas las fracciones en la matriz de fracciones que son equivalentes a 1/2. Haga esto encontrando 1/2 en la matriz, y viendo qué otros números tienen la misma longitud.
Utilice sus matrices de fracciones para determinar todas las fracciones en la matriz de fracciones que son equivalentes a 2/3. Haga esto encontrando 2/3 en la matriz, y viendo qué otros números tienen la misma longitud.
Ahora usarás tus múltiples tiras para identificar fracciones equivalentes. Para usar tus tiras, necesitas cortar las tiras por filas. Para encontrar fracciones equivalentes a 3/7, alinee la tira 3 por encima de la tira 7 como se muestra a continuación:
| 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 |
| 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 |
Ahora, se pueden ver otras once fracciones equivalentes para 3/7:6/14, 9/21, 12/28, 15/35, 18/42, 21/49, 24/56, 27/63, 30/70, 33/77, y 36/84.
Usa tus múltiples tiras para escribir 6 fracciones equivalentes a 2/9
Usa tus múltiples tiras para escribir 6 fracciones equivalentes a 4/5
¿Cuál es la regla para encontrar una fracción equivalente a una fracción dada? Dé un ejemplo de cómo encontrar algunas fracciones que equivalen a 5/6.
Ahora vamos a trabajar de nuevo con modelos, usando puntos, para comparar dos fracciones, sumar dos fracciones, restar dos fracciones, o multiplicar o dividir dos fracciones. Para cada problema, es CRUCIAL que comiences cada problema declarando explícitamente lo siguiente:
1. Sea específico sobre lo que está utilizando para la unidad. Será más fácil si usas una matriz de puntos, donde el denominador de una fracción es el número de filas en la matriz, y el denominador de la otra fracción es el número de columnas en la matriz.
2. Indique el valor de cada punto, cada columna y cada fila.
Bien, pasemos a un ejemplo: Usa modelos para comparar 2/5 y 3/7.
|
Paso 1: Dejar 1 unidad = 5 filas de puntos por 7 columnas de puntos, para un total de 35 puntos, como se muestra a continuación. Ya que hay 35 puntos a una unidad, cada punto = 1/35 de una unidad. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Paso 2: Dado que hay 5 filas, la unidad se puede dividir en 5 partes iguales dando vueltas a las filas, como se muestra a continuación:  Por lo tanto, cada fila es 1/5 de una unidad. Observe que hay 7 puntos en 1/5 de una unidad: 1/5 =\[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Paso 3: Del mismo modo, dado que hay 7 columnas iguales, cada columna es 1/7 de una unidad: 1/7 =\[ \begin{matrix} \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \end{matrix} \nonumber \] |
|
Paso 4: Ahora que ya hemos definido correctamente la unidad, estamos listos para mostrar qué aspecto tiene 2/5. Dado que 1/5 es 1 fila de puntos, entonces 2/5 debe ser 2 filas de puntos. Por lo tanto, a continuación se muestra 2/5: \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] Observe que 2/5 contiene 14 puntos, lo que equivale a 14/35. |
Paso 5: De igual manera, podemos mostrar cómo se ve 3/7. Ya que 1/7 es 1 columna de puntos, entonces 3/7 debe ser 3 columnas de puntos. Por lo tanto, a continuación se muestra 3/7: \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] Observe que 3/7 contiene 15 puntos, lo que equivale a 15/35. |
Dado que 2/5 contiene menos puntos que 3/7, 2/5 debe ser menor que 3/7. Respuesta: 2/5 < 3/7.
Compara 3/4 y 4/5 usando modelos. Mostrar todos los pasos, y explicar el procedimiento como se muestra en el ejemplo anterior.
Bien, pasemos a un ejemplo de adición: Usa modelos para agregar 2/5 y 3/7.
|
Paso 1: Dejar 1 unidad = 5 filas de puntos por 7 columnas de puntos, para un total de 35 puntos, como se muestra a continuación. Ya que hay 35 puntos a una unidad, cada punto = 1/35 de una unidad. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Paso 2: Dado que hay 5 filas, la unidad se puede dividir en 5 partes iguales dando vueltas a las filas, como se muestra a continuación:  Por lo tanto, cada fila es 1/5 de una unidad. Observe que hay 7 puntos en 1/5 de una unidad: 1/5 =\[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Paso 3: Del mismo modo, dado que hay 7 columnas iguales, cada columna es 1/7 de una unidad: 1/7 =\[ \begin{matrix} \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \end{matrix} \nonumber \] |
|
Paso 4: Ahora que ya hemos definido correctamente la unidad, estamos listos para mostrar qué aspecto tiene 2/5. Dado que 1/5 es 1 fila de puntos, entonces 2/5 debe ser 2 filas de puntos. Por lo tanto, a continuación se muestra 2/5: \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] Observe que 2/5 contiene 14 puntos, lo que equivale a 14/35. |
Paso 5: Ahora, sumamos los dos modelos juntos, como se muestra a continuación. La respuesta es 29/35. \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] Observe que 3/7 contiene 15 puntos, lo que equivale a 15/35. |
Paso 5: Ahora, sumamos los dos modelos juntos, como se muestra a continuación. La respuesta es 29/35.
\[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} + \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} = 29 \text{ dots } = 29/35 \nonumber \]
Agrega 1/4 y 2/5 usando modelos. Mostrar todos los pasos, y explicar el procedimiento como se muestra en el ejemplo anterior.
Bien, pasemos a un ejemplo de resta: Usa modelos para hacer la siguiente resta: 3/7 — 2/5.
|
Paso 1: Dejar 1 unidad = 5 filas de puntos por 7 columnas de puntos, para un total de 35 puntos, como se muestra a continuación. Ya que hay 35 puntos a una unidad, cada punto = 1/35 de una unidad. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Paso 2: Dado que hay 5 filas, la unidad se puede dividir en 5 partes iguales dando vueltas a las filas, como se muestra a continuación:  Por lo tanto, cada fila es 1/5 de una unidad. Observe que hay 7 puntos en 1/5 de una unidad: 1/5 =\[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Paso 3: Del mismo modo, dado que hay 7 columnas iguales, cada columna es 1/7 de una unidad: 1/7 =\[ \begin{matrix} \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \end{matrix} \nonumber \] |
|
Paso 4: Ahora que ya hemos definido correctamente la unidad, estamos listos para mostrar qué aspecto tiene 2/5. Dado que 1/5 es 1 fila de puntos, entonces 2/5 debe ser 2 filas de puntos. Por lo tanto, a continuación se muestra 2/5: \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] Observe que 2/5 contiene 14 puntos, lo que equivale a 14/35. |
Paso 5: De igual manera, podemos mostrar cómo se ve 3/7. Ya que 1/7 es 1 columna de puntos, entonces 3/7 debe ser 3 columnas de puntos. Por lo tanto, a continuación se muestra 3/7: \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] Observe que 3/7 contiene 15 puntos, lo que equivale a 15/35. |
Ahora, restamos, como se muestra a continuación. La respuesta es 1/35.
\[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} - \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} = 1 \text{ dot } = 1/35 \nonumber \]
Haga la siguiente resta usando modelos: 7/8 — 2/3. Mostrar todos los pasos, y explicar el procedimiento como se muestra en el ejemplo anterior.
Multiplicar fracciones es un poco más complicado. El modelo de suma repetida no tiene sentido cuando se multiplican dos fracciones. Cuando veas dos fracciones multiplicadas juntas, como 2/5\(\cdot\) 3/7, piensa en esto como 2/5 DE 3/7. Es decir, hay que tomar 3/7 de una unidad, y luego hay que tomar 2/5 de esa. Ten en cuenta que tienes que representar la segunda fracción ANTES de poder hacer la multiplicación.
Bien, pasemos a un ejemplo de multiplicación: Usa modelos para hacer la siguiente multiplicación: 2/5\(\cdot\) 3/7.
|
Paso 1: Dejar 1 unidad = 5 filas de puntos por 7 columnas de puntos, para un total de 35 puntos, como se muestra a continuación. Ya que hay 35 puntos a una unidad, cada punto = 1/35 de una unidad. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Paso 2: Dado que hay 5 filas, la unidad se puede dividir en 5 partes iguales. Por lo tanto, cada fila es 1/5 de una unidad. Observe que hay 7 puntos en 1/5 de una unidad: 1/5 =\[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Paso 3: Del mismo modo, dado que hay 7 columnas iguales, cada columna es 1/7 de una unidad: 1/7 =\[ \begin{matrix} \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \end{matrix} \nonumber \] |
|
Paso 4: Ahora que hemos definido correctamente la unidad, primero tenemos que mostrar cómo se ve 3/7 (el segundo número en la multiplicación). Ya que 1/7 es 1 columna de puntos, entonces 3/7 debe ser 3 columnas de puntos. Por lo tanto, a continuación se muestra 3/7: \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Paso 5: Aquí es donde hay una diferencia en cómo procedes. Ahora necesitas encontrar 2/5 del 3/7 que se muestra en el paso 4. Dado que hay 5 filas de puntos en el paso 4, cada fila (de 3 puntos) representa 1/5. Entonces, solo quieres 2 filas de los puntos del paso 4, como se muestra a continuación. \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] Esta es la respuesta. Hay 6 puntos, por lo que esto representa 6/35. |
La multiplicación se puede mostrar toda en una unidad mostrando primero la unidad, segundo dando vueltas a la parte que representa la segunda fracción en la multiplicación, y luego dando vueltas a la parte que representa la primera fracción en la multiplicación. A continuación se muestra la secuencia de pasos para este problema.
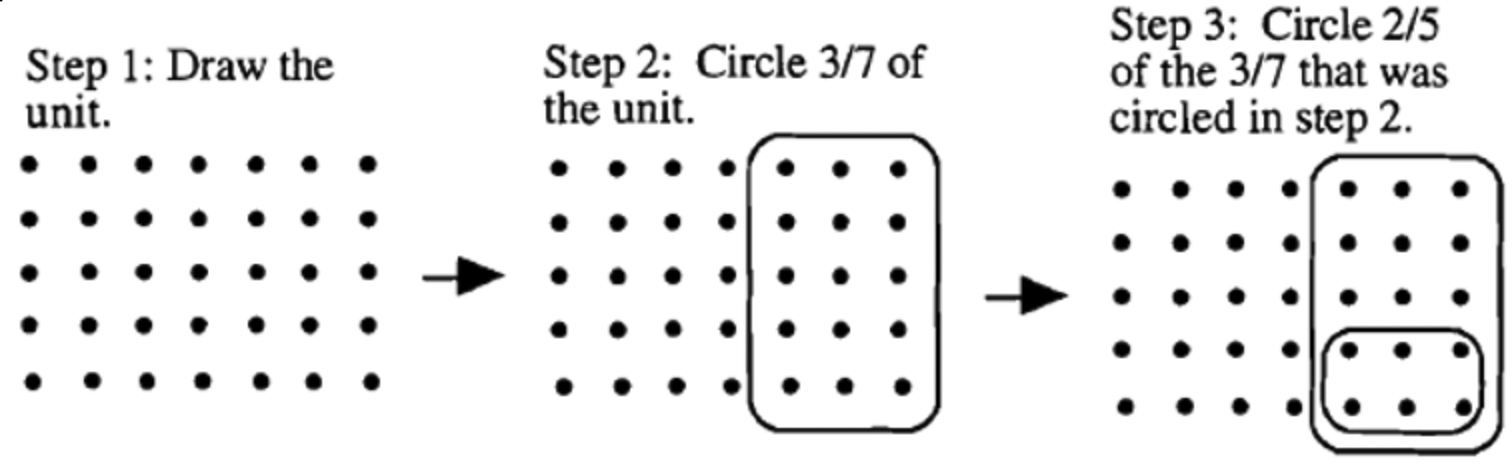
Bien, veamos cómo se ve si cambiamos el orden de las fracciones: Usa modelos para hacer la siguiente multiplicación:\(\bf 3/7 \cdot 2/5\).
|
Paso 1: Dejar 1 unidad = 5 filas de puntos por 7 columnas de puntos, para un total de 35 puntos, como se muestra a continuación. Hay 35 puntos a una unidad, por lo que cada punto = 1/35 de una unidad. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Paso 2: Dado que hay 5 filas, la unidad se puede dividir en 5 partes iguales. Por lo tanto, cada fila es 1/5 de una unidad. Observe que hay 7 puntos en 1/5 de una unidad: 1/5 =\[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Paso 3: Del mismo modo, dado que hay 7 columnas iguales, cada columna es 1/7 de una unidad: 1/7 =\[ \begin{matrix} \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \end{matrix} \nonumber \] |
|
Paso 4: Ahora que hemos definido correctamente la unidad, primero tenemos que mostrar qué aspecto tiene 2/5 (el segundo número en la multiplicación). Dado que 1/5 es 1 columna de puntos, entonces 2/5 debe ser 2 columnas de puntos. Por lo tanto, a continuación se muestra 2/5: \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Paso 5: Ahora necesitas encontrar 3/7 del 2/5 que se muestra en el paso 4. Dado que hay 7 columnas de puntos en el paso 4, cada columna (de 2 puntos) representa 1/7. Entonces, solo quieres 3 filas de los puntos del paso 4, como se muestra a continuación. \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] Esta es la respuesta. Hay 6 puntos, por lo que esto representa 6/35. |
Nuevamente, esta multiplicación puede mostrarse toda en una unidad mostrando primero la unidad, segundo dando vueltas a la parte que representa la segunda fracción en la multiplicación, y luego dando vueltas a la parte que representa la primera fracción en la multiplicación. A continuación se muestra la secuencia de pasos para este problema.
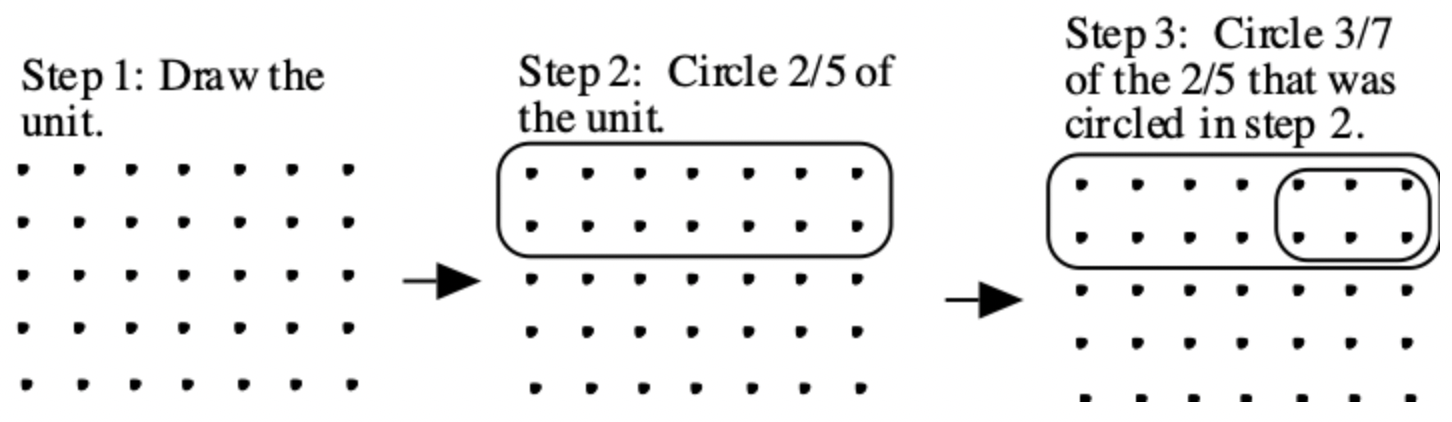
Si bien la respuesta es la misma para 3/7\(\cdot\) 2/5, y 2/5\(\cdot\) 3/7, la secuencia de pasos no lo es. Anote la diferencia entre el paso 3 anterior (3/7\(\cdot\) 2/5) y el paso 3 a continuación (2/5\(\cdot\) 3/7).
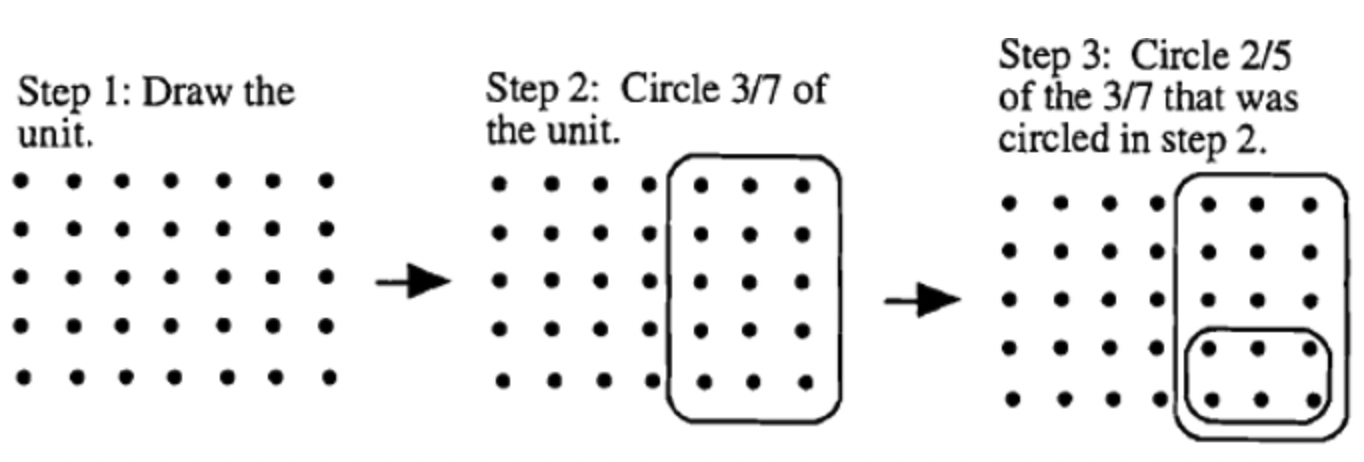
Haz las siguientes multiplicaciones usando modelos. Mostrar todos los pasos y explicar el procedimiento como se muestra en los ejemplos anteriores.
a. 4/5\(\cdot\) 2/3
b. 3/4\(\cdot\) 5/6
Al mirar el dibujo final alguien hizo para modelar una multiplicación de dos fracciones, determinar qué multiplicación se realizó, y luego exponer la respuesta. Círculo cuya multiplicación representa la elección correcta.
|
a. 5/6\(\cdot\) 2/3 O 2/3\(\cdot\) 5/6 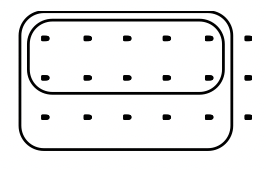 |
b. 1/2\(\cdot\) 7/8 O 7/8\(\cdot\) 1/2 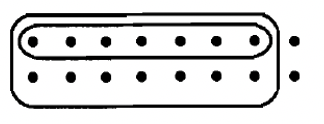 |
Si todos los puntos mostrados para cada problema representan 1 unidad, determine el problema de multiplicación que alguien hizo para obtener la respuesta, e indique la respuesta.
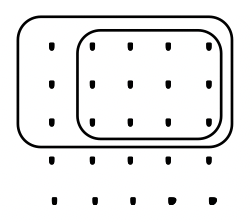 a. a. |
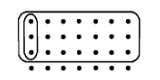 b. b. |
Otro modelo que puedes usar para hacer multiplicación son las tiras C, aunque es algo limitante.
Multiplicar\(3/4 \cdot 1/2\).
Solución
Esto significa 3/4 de 1/2 de una unidad. Entonces, tendremos que definir una unidad apropiada, primero tomar 1/2 de la unidad, y luego tomar 3/4 de la respuesta obtenida después de tomar 1/2. La opción para 1 unidad usando tiras en C es multiplicar los denominadores juntos para obtener la longitud de la varilla unitaria que necesita. En este caso, 4\(\cdot\) 2 = 8, así que elige la tira C Marrón como unidad.
Dejar 1 unidad = N. Primero, tomar 1/2 de Brown (N), que es púrpura (P). Después, toma 3/4 de púrpura, que es verde claro (L). La respuesta, L, representa 3/8, ya que la unidad C-tira fue N. Por lo tanto, 3/4\(\cdot\) 1/2 = 3/8.
Multiplicar\(1/2 \cdot 3/4\).
Solución
Esto significa 1/2 de 3/4 de una unidad. Entonces, tendremos que definir una unidad apropiada, primero tomar 3/4 de la unidad, y luego tomar 1/2 de la respuesta obtenida después de tomar 3/4. La opción para 1 unidad usando tiras en C es multiplicar los denominadores juntos para obtener la longitud de la varilla unitaria que necesita. En este caso, 4\(\cdot\) 2 = 8, así que elige la tira C Marrón como unidad.
Dejar 1 unidad = N. Primero, tomar 3/4 de Marrón (N), que es verde oscuro (D). Después, tomar 1/42 de verde oscuro (D), que es verde claro (L). La respuesta, L, representa 3/8, ya que la unidad C-tira fue N. Por lo tanto, 1/2\(\cdot\) 3/4 = 3/8.
Multiplicar\(2/3 \cdot 4/5\).
Solución
Esto significa 2/3 de 4/5 de una unidad. Entonces, tendremos que definir una unidad apropiada, primero tomar 4/5 de la unidad, y luego tomar 2/3 de la respuesta obtenida después de tomar 4/5. La opción para 1 unidad usando tiras en C es multiplicar los denominadores juntos para obtener la longitud de la varilla unitaria que necesita. En este caso, 3\(\cdot\) 5 = 15. No hay una tira en C tan larga, así que usa y naranja + amarillo como unidad.
Dejar 1 unidad = O + Y. Primero, tomar 4/5 de O + Y, que es rosa intenso (H). Después, tomar 2/3 de rosa fuerte (H), que es marrón (N). La respuesta, N, representa 8/15, ya que la unidad C-tira fue O + Y. Por lo tanto, 2/3\(\cdot\) 4/5 = 8/15.
Usa las tiras C para multiplicar 1/3\(\cdot\) 3/4. Explique los pasos.
El proceso de hacer multiplicación usando tiras en C se puede mostrar en un gráfico. He mostrado los pasos para los tres ejemplos anteriores en la página siguiente.
Rellene el gráfico mostrando cómo hacer las siguientes multiplicaciones usando tiras C. La multiplicación está en la primera columna. Anote una opción apropiada para la unidad (nombre una tira C, o la suma de dos tiras en C) en la segunda columna. Escribe la tira C obtenida después de la primera parte de la multiplicación (que es la segunda fracción como parte de la unidad) en la tercera columna. Después, haz la multiplicación final, y escribe la tira C obtenida en la cuarta columna. En la quinta columna, escribe una fracción usando tiras C poniendo la unidad final obtenida en la cuarta columna como numerador, y la unidad en el denominador. Después, en la última columna, escribe la respuesta como una fracción. No simplifique.
| Ejemplo | \(3/4 \cdot 1/2\) | N | P | L | \(\frac{L}{N}\) | \(\frac{3}{8}\) |
| Ejemplo | \(1/2 \cdot 3/4\) | N | D | L | \(\frac{L}{N}\) | \(\frac{3}{8}\) |
| Ejemplo | \(2/3 \cdot 4/5\) | O+Y | H | N | \(\frac{N}{O+R}\) | \(\frac{8}{15}\) |
| a. | \(1/3 \cdot 3/4\) | |||||
| b. | \(1/2 \cdot 1/4\) | |||||
| c. | \(3/2 \cdot 1/4\) | |||||
| d. | \(2/3 \cdot 1/2\) |
On to División con Números Racionales...
Recuerda que la respuesta a la división se\(\bf a \div b\) puede obtener respondiendo a esta pregunta: "¿Cuántos conjuntos de b están contenidos en a?”
Usemos esta idea para encontrar la respuesta al siguiente problema de división:
Utilice un modelo para calcular:\(\bf 3 \div 1/2\)
Solución
La respuesta a\(\bf 3 \div 1/2\) es la respuesta a esta pregunta: ¿Cuántos 1/2 están contenidos en 3? A continuación se presentan dos métodos posibles que puede utilizar para encontrar la solución.
Método 1: Dejar 1 unidad = 1 cuadrado. Después cuente cuántos 1/2 están contenidos en 3 cuadrados.
Dibuja tres cuadrados para representar 3. Luego, divida cada cuadrado en 1/2. Cuenta cuántas 1/2 hay en los 3 cuadrados. Del modelo, está claro que hay 6 1/2's en 3 cuadrados. Entonces la respuesta a 3\(\div\) 1/2 es 6.
Método 2: Que la unidad se defina de manera similar a como la hicimos para los problemas anteriores.Multiplique los denominadores juntos para determinar cuántos puntos hay en una unidad. En este caso, 3 es lo mismo que 3/1. Deje que la unidad = 1 fila de puntos por 2 columnas de puntos para un total de 2 puntos.
Unidad =\(\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix}\) Luego representar el número 3 con base en esta unidad, y el número 1/2 basado en esta unidad.
3 = 3 conjuntos de 2 puntos =\(\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix}\) y 1/2 = 1/2 de los 2 puntos =\(\boldsymbol{\cdot}\)
En el conjunto que representa 3, circule tantos conjuntos como sea posible que representen 1/2:\(\begin{matrix} \boldsymbol{\boxdot} & \boldsymbol{\boxdot} & \boldsymbol{\boxdot} & \boldsymbol{\boxdot} & \boldsymbol{\boxdot} & \boldsymbol{\boxdot} \end{matrix}\)
Cuenta cuántos 1/2 hay en 3. Hay 6 1/2 en 3, así que la respuesta es 6.
Método 3: Dejar 1 unidad = la tira C verde oscuro. Representan 3 y 1/2 como una tira en C basada en esta unidad. Desde 3 = 3 tiras C de color verde oscuro, luego 3 = la tira C naranja + marrón (o 3 verdes oscuros, o rosa fuerte + verde oscuro). Dado que 1/2 de la tira C verde oscuro es verde claro, entonces 1/2 = la tira C verde claro.
Tenemos que responder a la pregunta: ¿Cuántos 1/2 hay en 3? Dado que 1/2 = L, y 3 = O + N, cuente cuántas tiras en C de color verde claro conforman la longitud de la tira C O + N. Hay 6. Una vez más, la respuesta es 6.
| Unidad: | D |
|---|
| 3: | H | D |
|---|
| 1/2 | L |
|---|
Aquí te explicamos cómo obtener la respuesta. Mostrar cuántos verdes claros están contenidos rosa intenso + verde oscuro.
| L | L | L | L | L | L |
Observe que comienza definiendo una tira C de unidad y, a continuación, usa esa unidad para definir los dos números en el problema de división. Pero NO se refiere de nuevo a la unidad para calcular el problema de división. Simplemente cuenta cuántos del divisor (segunda tira C) hay en el dividendo (primera tira C).
Utilice un modelo para calcular:\(\bf 1/2 \div 1/4\).
Solución
La respuesta a\(\bf 1/2 \div 1/4\) es la respuesta a esta pregunta: ¿Cuántos 1/4 están contenidos en 1/2?
Dejar 1 unidad = 2 filas de puntos por 4 columnas de puntos:
\[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \]
Después representar el número 1/2 basado en esta unidad, y el número 1/4 basado en esta unidad.
1/2 =\( \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot}\end{matrix} \) y 1/4 =\(\begin{matrix} \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \end{matrix}\)
En el conjunto que representa 1/2, circule tantos conjuntos como sea posible que representen 1/4:
Cuenta cuántos 1/4 hay en 1/2. Hay 2 1/4 en 1/2, así que la respuesta es 2.
Esto también se puede hacer usando tiras en C. Dejar la unidad = N. Entonces 1/2 = P y 1/4 = R. Ya que hay 2 rojos en la tira C morada, 1/2\(\div\) 1/4 = 2.
Utilice un modelo para hacer la siguiente división: 1/5\(\div\) 1/10. Use cajas, puntos o tiras en C. Primero defina la unidad. Después explica y muestra todos los pasos.
Realice la siguiente división utilizando cada uno de los métodos (cajas, puntos, tiras en C):
1/3\(\div\) 1/9. Primero defina la unidad. Después explica y muestra todos los pasos.
Realice la siguiente división utilizando cada uno de los métodos (cajas, puntos, tiras en C):
2/3\(\div\) 1/6. Primero defina la unidad. Después explica y muestra todos los pasos.
Realice la siguiente división utilizando cada uno de los métodos (cajas, puntos, tiras en C):
3\(\div\) 1/4. Primero defina la unidad. Después explica y muestra todos los pasos.


