8.4: Probabilidad Condicional
- Page ID
- 113768
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En esta sección, aprenderás a:
- reconocer situaciones que implican probabilidad condicional
- calcular probabilidades condicionales
Supongamos que un amigo te pregunta la probabilidad de que hoy nieva.
Si estás en Boston, Massachusetts en invierno, la probabilidad de nieve hoy podría ser bastante sustancial. Si estás en Cupertino, California en verano, la probabilidad de nieve hoy es muy diminuta, esta probabilidad es prácticamente 0.
Dejar:
- \(\mathrm{A}\)= el suceso que hoy va a nevar
- \(\mathrm{B}\)= el evento que hoy estás en Boston en invierno
- \(\mathrm{C}\)= el evento que hoy estás en Cupertino en verano
Debido a que la probabilidad de nieve se ve afectada por la ubicación y época del año, no podemos simplemente escribir\(\mathrm{P(A)}\) para la probabilidad de nieve. Necesitamos indicar la otra información que conocemos -ubicación y época del año. Necesitamos usar probabilidad condicional.
El evento que nos interesa es evento\(\mathrm{A}\) para nieve. El otro evento se llama la condición, representando la ubicación y época del año en este caso.
Representamos probabilidad condicional usando una línea vertical | que significa “si”, o “dado eso”, o “si sabemos eso”. El evento de interés aparece a la izquierda del |. El estado aparece en el lado derecho del |.
La probabilidad de que nieva dado que (si) estás en Boston en el invierno está representado por\(\mathbf{P} \left( \mathbf{A} | \mathbf{B}\right) \). En este caso, la condición es\(\mathrm{B}\).
La probabilidad de que nieva dado que (si) estás en Cupertino en el verano está representada por\(\mathbf{P}(\mathbf{A} | \mathbf{C})\). En este caso, la condición es\(\mathrm{C}\).
Ahora, examinemos una situación en la que podamos calcular algunas probabilidades.
Supongamos que usted y un amigo juegan un juego que implica elegir una sola carta de una baraja bien barajada. Tu amigo te reparte una carta, boca abajo, de la baraja y te ofrece el siguiente trato: Si la carta es un rey, te pagará $5, de lo contrario, tú le pagas $1. ¿Deberías jugar el juego?
Razón de la siguiente manera. Dado que hay cuatro reyes en la baraja, la probabilidad de obtener un rey es 4/52 o 1/13. Entonces, la probabilidad de no obtener un rey es 12/13. Esto implica que la relación entre tu ganancia y pérdida es de 1 a 12, mientras que la relación de pagos es de solo $1 a $5. Por lo tanto, determinas que no debes jugar.
Pero considera el siguiente escenario. Mientras tu amigo estaba repartiendo la tarjeta, por casualidad te la echaste un vistazo y notaste que la tarjeta era una tarjeta facial. ¿Deberías, ahora, jugar el juego?
Dado que hay 12 cartas de cara en la baraja, los elementos totales en el espacio de muestra ya no son 52, sino solo 12. Esto significa que la probabilidad de obtener un rey es 4/12 o 1/3. Entonces tu probabilidad de ganar es 1/3 y de perder 2/3. Esto hace que su relación ganador/perdedor sea de 1 a 2, que le va mucho mejor con la relación de pagos de $1 a $5. Esta vez, determinas que debes jugar.
En la segunda parte del ejemplo anterior, estábamos encontrando la probabilidad de obtener un rey sabiendo que se había mostrado una carta facial. Este es un ejemplo de probabilidad condicional. Siempre que estamos encontrando la probabilidad de un evento\(\mathrm{E}\) bajo la condición de que\(\mathrm{F}\) haya ocurrido otro evento, estamos encontrando probabilidad condicional.
El símbolo\(\mathrm{P(E | F)}\) denota el problema de encontrar la probabilidad de\(\mathrm{E}\) dado que\(\mathrm{F}\) ha ocurrido. Leemos\(\mathrm{P(E | F)}\) como “la probabilidad de\(\mathrm{E}\), dada”\(\mathrm{F}\).
Una familia tiene tres hijos. Encuentra la probabilidad condicional de tener dos hijos y una niña dado que el primogénito es un niño.
Solución
Que el evento\(\mathrm{E}\) sea que la familia tenga dos hijos y una niña, y\(\mathrm{F}\) que el primogénito sea un niño.
Primero, tenemos el espacio muestral para una familia de tres hijos de la siguiente manera.
\[S = \{BBB, BBG, BGB, BGG, GBB, GBG, GGB, GGG\} \nonumber \]
Como sabemos que el primogénito es un niño, nuestras posibilidades se reducen a cuatro resultados: BBB, BBG, BGB y BGG.
Entre los cuatro, BBG y BGB representan a dos niños y una niña.
Por lo tanto,\(\mathrm{P(E | F)}\) = 2/4 o 1/2.
Un troquel de seis lados se enrolla una vez.
- Encuentra la probabilidad de que el resultado sea parejo.
- Encuentra la probabilidad de que el resultado sea incluso dado que el resultado sea mayor a tres.
Solución
El espacio muestral es\(\mathrm{S} = {1,2,3,4,5,6}\)
Que evento\(\mathrm{E}\) sea que el resultado sea parejo y\(\mathrm{T}\) sea que el resultado sea mayor a 3.
a.\(\mathrm{P(E)}\) = 3/6 porque\(\mathrm{E} = {2,4,6}\)
b. Porque\(T = {4,5,6}\) sabemos que 1, 2, 3 no puede ocurrir; solo los resultados 4, 5, 6 son posibles. Por lo tanto de los valores en\(\mathrm{E}\), sólo 4, 6 son posibles.
Por lo tanto,\(\mathrm{P(E|T)}\) = 2/3
Una moneda justa es tirada dos veces.
- Encuentra la probabilidad de que el resultado sea de dos cabezas.
- Encuentra la probabilidad de que el resultado sea de dos cabezas dado que se obtiene al menos una cabeza.
Solución
El espacio muestral es \(S = {HH, HT, TH, TT}\)
\(\mathrm{E}\)Sea el evento que se obtengan las dos cabezas y\(\mathrm{F}\) se obtenga al menos una cabeza
a.\(\mathrm{P(E)}\) = 1/4 porque\(\mathrm{E} = {HH}\) y el espacio muestral\(\mathrm{S}\) tiene 4 resultados.
b\(\mathrm{F} = {HH, HT, TH}\). Dado que se obtuvo al menos una cabeza, no se presentó TT.
Estamos interesados en el evento de probabilidad\(\mathrm{E}={HH}\) de los 3 resultados en el espacio muestral reducido F.
Por lo tanto,\(\mathrm{P(E|F)}\) = 1/3
Desarrollemos ahora una fórmula para la probabilidad condicional\(\mathrm{P(E | F)}\).
Supongamos que un experimento consiste en eventos\(n\) igualmente probables. Supongamos además que hay\(m\) elementos en\(\mathrm{F}\), y\(c\) elementos en\(\mathrm{E} \cap \mathrm{F}\), como se muestra en el siguiente diagrama de Venn.
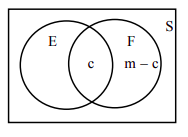
Si el evento\(\mathrm{F}\) ha ocurrido, el conjunto de todos los resultados posibles ya no es el espacio muestral completo, sino el subconjunto\(\mathrm{F}\). Por lo tanto, solo miramos al set\(\mathrm{F}\) y a nada fuera de\(\mathrm{F}\). Ya que\(\mathrm{F}\) tiene\(m\) elementos, el denominador en el cálculo de\(\mathrm{P(E | F)}\) es\(m\). Podemos pensar que el numerador para nuestra probabilidad condicional es el número de elementos en\(\mathrm{E}\). Pero claramente no podemos considerar los elementos de\(\mathrm{E}\) que no están en\(\mathrm{F}\). Sólo podemos contar los elementos de\(\mathrm{E}\) que están en\(\mathrm{F}\), es decir, los elementos en\(\mathrm{E} \cap \mathrm{F}\). Por lo tanto,
\[\mathrm{P}(\mathrm{E} | \mathrm{F})=\frac{\mathrm{c}}{\mathrm{m}} \nonumber \]
Dividiendo tanto el numerador como el denominador por\(n\), obtenemos
\[\mathrm{P(E | F)}=\frac{c / n}{m / n} \nonumber \]
Pero\(c/n = \mathrm{P}(\mathrm{E} \cap \mathrm{F})\), y\(m/n = \mathrm{P}(\mathrm{F})\).
Sustituyendo, derivamos la siguiente fórmula para\(\mathrm{P}(\mathrm{E} | \mathrm{F})\).
Para dos eventos\(\mathrm{E}\) y\(\mathrm{F}\), la probabilidad de "\(\mathrm{E}\)Dado\(\mathrm{F}\)" es
\[\mathbf{P}(\mathbf{E} | \mathbf{F})=\frac{\mathbf{P}(\mathbf{E} \cap \mathbf{F})}{\mathbf{P}(\mathbf{F})} \nonumber \]
Se enrolla una sola matriz. Utilice la fórmula anterior para encontrar la probabilidad condicional de obtener un número par dado que se ha mostrado un número mayor a tres.
Solución
\(\mathrm{E}\)Sea el evento que muestra un número par, y\(\mathrm{F}\) ser el evento que muestra un número mayor a tres. Nosotros queremos\(\mathrm{P}(\mathrm{E} | \mathrm{F})\).
\(\mathrm{E} = {2, 4, 6}\)y\(\mathrm{F} = {4, 5, 6}\). Lo que implica,\(\mathrm{E} \cap \mathrm{F} = { 4, 6}\)
Por lo tanto,\(\mathrm{P}(\mathrm{F})\) = 3/6, y\(\mathrm{P}(\mathrm{E} \cap \mathrm{F})\) = 2/6
\[P(E | F)=\frac{P(E \cap F)}{P(F)}=\frac{2 / 6}{3 / 6}=\frac{2}{3} \nonumber. \nonumber \]
En la siguiente tabla se muestra la distribución por género de los estudiantes de un colegio comunitario que toman el transporte público y los que conducen a la escuela.
| Macho (M) | Hembra (F) | Total | |
| Transporte Público (T) | 8 | 13 | 21 |
| Accionamiento (D) | 39 | 40 | 79 |
| Total | 47 | 53 | 100 |
Los eventos\(\mathrm{M}, \mathrm{F}, \mathrm{T}\), y\(\mathrm{D}\) son autoexplicativos. Encuentra las siguientes probabilidades.
- \(\mathrm{P}(\mathrm{D} | \mathrm{M})\)
- \(\mathrm{P}(\mathrm{F} | \mathrm{D})\)
- \(\mathrm{P}(\mathrm{M} | \mathrm{T})\)
Solución 1
Las probabilidades condicionales a menudo se pueden encontrar directamente de una tabla de contingencia. Si la condición corresponde a una sola fila o a una sola columna de la tabla, entonces puede ignorar el resto de la tabla y leer la probabilidad condicional directamente desde la fila o columna indicada por la condición.
- La condición es evento\(\mathrm{M}\); podemos mirar solo la columna “Male” de la tabla e ignorar el resto de la mesa:\(\mathrm{P}(\mathrm{D} | \mathrm{M})=\frac{39}{47}\).
- La condición es evento\(\mathrm{D}\); podemos mirar solo la fila “Drive” de la mesa e ignorar el resto de la mesa:\(\mathrm{P}(\mathrm{F} | \mathrm{D})=\frac{40}{79}\).
- La condición es evento\(\mathrm{T}\); podemos mirar solo la fila “Transporte Público” de la mesa e ignorar el resto de la mesa:\(\mathrm{P}(\mathrm{M} | \mathrm{T})=\frac{8}{21}\).
Solución 2
Utilizamos la fórmula de probabilidad condicional\(\mathrm{P}(\mathrm{E} | \mathrm{F})=\frac{\mathrm{P}(\mathrm{E} \cap \mathrm{F})}{\mathrm{P(F)}}\).
- \[P(D | M)=\frac{P(D \cap M)}{P(M)}=\frac{39 / 100}{47 / 100}=\frac{39}{47} \nonumber . \nonumber \]
- \[P(F | D)=\frac{P(F \cap D)}{P(D)}=\frac{40 / 100}{79 / 100}=\frac{40}{79} \nonumber . \nonumber \]
- \[\mathrm{P}(\mathrm{M} | \mathrm{T})=\frac{P(M \cap T)}{P(T)}=\frac{8 / 100}{21 / 100}=\frac{8}{21} \nonumber \]
Dado\(\mathrm{P(E)}\) = .5,\(\mathrm{P}(\mathrm{F})\) = .7, y\(\mathrm{P}(\mathrm{E} \cap \mathrm{F})\) = .3. Encuentra lo siguiente:
- \(\mathrm{P}(\mathrm{E} | \mathrm{F})\)
- \(\mathrm{P}(\mathrm{F} | \mathrm{E})\)
Solución
Utilizamos la fórmula de probabilidad condicional.
- \(P(E | F)=\frac{P(E \cap F)}{P(F)}=\frac{3}{7}=\frac{3}{7}\)
- \(P(F | E)=\frac{P(E \cap F)}{P(E)}=.3 / .5=3 / 5 \)
\(\mathrm{E}\)y\(\mathrm{F}\) son eventos mutuamente excluyentes tales que\(\mathrm{P(E)}\) = .4,\(\mathrm{P(F)}\) = .9. Encuentra\(\mathrm{P(E | F)}\).
Solución
\(\mathrm{E}\)y\(\mathrm{F}\) son mutuamente excluyentes, por lo que\(\mathrm{P}(\mathrm{E} \cap \mathrm{F})\) = 0.
Por lo tanto\(\mathrm{P}(\mathrm{E} | \mathrm{F})=\frac{\mathrm{P}(\mathrm{E} \cap \mathrm{F})}{\mathrm{P}(\mathrm{F})}=\frac{0}{9}=0\).
Dado\(\mathrm{P}(\mathrm{F} | \mathrm{E})\) = .5, y\(\mathrm{P}(\mathrm{E} \cap \mathrm{F})\) = .3. Encuentra\(\mathrm{P}(\mathrm{E})\).
Solución
Usando la fórmula de probabilidad condicional\(\mathrm{P}(\mathrm{E} | \mathrm{F})=\frac{\mathrm{P}(\mathrm{E} \cap \mathrm{F})}{\mathrm{P}(\mathrm{F})}\), obtenemos
\[\mathrm{P}(\mathrm{F} | \mathrm{E})=\frac{\mathrm{P}(\mathrm{E} \cap \mathrm{F})}{\mathrm{P}(\mathrm{E})} \nonumber \]
Sustitución y resolución:
\[.5=\frac{.3}{\mathrm{P}(\mathrm{E})} \quad \text { or } \quad \mathrm{P}(\mathrm{E})=3 / 5 \nonumber \]
En una familia de tres hijos, encuentra la probabilidad condicional de tener dos hijos y una niña, dado que la familia tiene al menos dos niños.
Solución
Que el evento\(\mathrm{E}\) sea que la familia tenga dos hijos y una niña, y que\(\mathrm{F}\) sea la probabilidad de que la familia tenga al menos dos niños. Nosotros queremos\(\mathrm{P}(\mathrm{E} | \mathrm{F})\).
Enumeramos el espacio de muestra junto con los eventos\(\mathrm{E}\) y\(\mathrm{F}\).
\ begin {alineado}
&\ mathrm {S} =\ {\ mathrm {BBB},\ mathrm {BBG},\ mathrm {BGB},\ mathrm {BGG},\ mathrm {GBB},\ mathrm {GBG},\ mathrm {GGB},\ mathrm {GGG}\}\\
&\ mathrm {E} =\ {\ mathrm rm {BBG},\ mathrm {BGB},\ mathrm {GBB}\}\ texto {y}\ mathrm {F} =\ {\ mathrm {BBB},\ mathrm {BBG},\ mathrm {BGB},\ mathrm {GBB}\}\\
&\ mathrm {E}\ cap\ mathrm {F} =\ {\ mathrm {BBG},\ mathrm {BGB},\ mathrm {GBB}\}
\ end {alineado}
Por lo tanto,\(\mathrm{P}(\mathrm{F})\) = 4/8, y\(\mathrm{P}(\mathrm{E} \cap \mathrm{F})\) = 3/8, y
\[\mathrm{P}(\mathrm{E} | \mathrm{F})=\frac{\mathrm{P}(\mathrm{E} \cap \mathrm{F})}{\mathrm{P}(\mathrm{E})} =\frac{3/8}{4/8} =\frac{3}{4} \nonumber. \nonumber \]
En un colegio comunitario el 65% de los estudiantes se suscribe a Amazon Prime, el 50% se suscribe a Netflix y el 20% se suscribe a ambos. Si un alumno es elegido al azar, encuentra las siguientes probabilidades:
- el estudiante se suscribe a Amazon Prime dado que se suscribe a Netflix
- el estudiante se suscribe a Netflix dado que se suscribe a Amazon Prime
Solución
\(\mathrm{A}\)Sea el evento que el estudiante suscriba a Amazon Prime, y\(\mathrm{N}\) sea el evento que el estudiante suscriba a Netflix.
Primero identificar las probabilidades y eventos dados en el problema.
\(\mathrm{P}\)(estudiante se suscribe a Amazon Prime) =\(\mathrm{P(A)}\) = 0.65
\(\mathrm{P}\)(estudiante se suscribe a Netflix) =\(\mathrm{P(N)}\) = 0.50
\(\mathrm{P}\)(estudiante se suscribe tanto a Amazon Prime como a Netflix) =\(\mathrm{P(A \cap N)}\) = 0.20
Luego usa la regla de probabilidad condicional:
- \(\mathrm{P}(\mathrm{A} | \mathrm{N})=\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{N})}{\mathrm{P}(\mathrm{N})} = \frac{.20}{.50} = \frac{2}{5}\)
- \(\mathrm{P}(\mathrm{N} | \mathrm{A})=\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{N})}{\mathrm{P}(\mathrm{A})} = \frac{.20}{.65} = \frac{4}{13}\)


