7.2: Interés Compuesto
- Page ID
- 113090
Con simple interés, estábamos asumiendo que nos embolsamos el interés cuando lo recibimos. En una cuenta bancaria estándar, cualquier interés que ganemos se agrega automáticamente a nuestro saldo, y ganamos intereses sobre ese interés en años futuros. Esta reinversión de intereses se llama capitalización.
Supongamos que depositamos $1,000 en una cuenta bancaria ofreciendo 3% de interés, compuesto mensualmente. ¿Cómo crecerá nuestro dinero?
El interés del 3% es una tasa porcentual anual (TAE) — el interés total a pagar durante el año. Dado que los intereses se pagan mensualmente, cada mes, ganaremos\(\dfrac{3 \%}{12} = 0.25 \%\) por mes.
En el primer mes,
\(P_0 = $1000\)
\(r = 0.0025 (0.25\%) \)
\(I = $1000 (0.0025) = $2.50\)
\(A = $1000 + $2.50 = $1,002.5\)
En el primer mes, ganaremos $2.50 en intereses, elevando el saldo de nuestra cuenta a $1,002.50. En el segundo mes,
\(P_0 = $1,002.50\)
\(I = $1002.50 (0.0025) = $2.51\)(redondeado)
\(A = $1002.50 + $2.51 = $1005.01\)
Observe que en el segundo mes ganamos más intereses que en el primer mes. Esto se debe a que ganamos intereses no solo sobre los $1,000 originales que depositamos, sino que también ganamos intereses sobre los $2.50 de intereses que ganamos el primer mes. Esta es la ventaja clave que nos da la capitalización de intereses.
Calculando unos meses más:
| Mes | Saldo inicial | Intereses devengados | Saldo final |
|---|---|---|---|
| 1 | 1000.00 | 2.50 | 1002.50 |
| 2 | 1002.50 | 2.50 | 1005.01 |
| 3 | 1005.01 | 2.51 | 1007.52 |
| 4 | 1007.52 | 2.52 | 1010.04 |
| 5 | 1010.04 | 2.53 | 1012.57 |
| 6 | 1012.57 | 2.53 | 1015.10 |
| 7 | 1015.10 | 2.54 | 1017.64 |
| 8 | 1017.64 | 2.54 | 1020.18 |
| 9 | 1020.18 | 2.55 | 1022.73 |
| 10 | 1022.73 | 2.56 | 1025.29 |
| 11 | 1025.29 | 2.56 | 1027.85 |
| 12 | 1027.85 | 2.57 | 1030.42 |
Para encontrar una ecuación que represente esto, si\(P_m\) representa la cantidad de dinero después de\(m\) meses, entonces podríamos escribir la ecuación recursiva:
\(P_0 = $1000\)
\(P_m = (1+0.0025)P_{m-1}\)
Probablemente reconozcas esto como la forma recursiva de crecimiento exponencial. Si no, podríamos pasar por los pasos para construir una ecuación explícita para el crecimiento:
\(P_0 = $1000\)
\(P_1 = 1.0025P_0 = 1.0025 (1000)\)
\(P_2 = 1.0025P_1 = 1.0025 (1.0025 (1000)) = 1.0025 2 (1000)\)
\(P_3 = 1.0025P_2 = 1.0025 (1.00252 (1000)) = 1.00253 (1000)\)
\(P_4 = 1.0025P_3 = 1.0025 (1.00253 (1000)) = 1.00254 (1000)\)
Observando un patrón, podríamos concluir
\(P_m = (1.0025)^m($1000)\)
Observe que los $1000 en la ecuación era\(P_0\), el monto inicial. Encontramos 1.0025 al sumar uno a la tasa de crecimiento dividida por 12 ya que estábamos componiendo 12 veces al año. Generalizando nuestro resultado, podríamos escribir
\[P_m = P_0 \left(1 + \dfrac{r}{k} \right)^m \nonumber \]
En esta fórmula:
- \(m\)es el número de periodos compuestos (meses en nuestro ejemplo)
- \(r\)es la tasa de interés anual
- \(k\)es el número de compuestos por año.
Si bien esta fórmula funciona bien, es más común usar una fórmula que involucre el número de años, en lugar del número de períodos compuestos. Si\(N\) es el número de años, entonces\(m=Nk\). Hacer este cambio nos da la fórmula estándar para el interés compuesto.
\[P_N = P_0 \left(1 + \dfrac{r}{k} \right)^{Nk} \nonumber \]
- \(P_N\)es el saldo en la cuenta después de\(N\) años.
- \(P_0\)es el saldo inicial de la cuenta (también llamado depósito inicial, o principal)
- \(r\)es la tasa de interés anual en forma decimal
- \(k\)es el número de períodos compuestos en un año.
Si la composición se realiza anualmente (una vez al año),\(k = 1\).
Si la capitalización se realiza trimestralmente,\(k = 4\).
Si la composición se realiza mensualmente,\(k = 12\).
Si la composición se realiza diariamente,\(k = 365\).
Lo más importante a recordar sobre el uso de esta fórmula es que supone que ponemos dinero en la cuenta una vez y dejamos que se quede ahí ganando intereses.
Un certificado de depósito (CD) es un instrumento de ahorro que muchos bancos ofrecen. Por lo general, da una tasa de interés más alta, pero no puede acceder a su inversión por un período de tiempo específico. Supongamos que deposita $3000 en un CD pagando 6% de interés, compuesto mensualmente. ¿Cuánto tendrá en la cuenta después de 20 años?
Solución
En este ejemplo,
El depósito inicial:
\(P_0 = $3000\)
6% anual:
\(r = 0.06\)
12 meses en 1 año:
\(k = 12\)
Ya que estamos buscando cuánto tendremos después de 20 años
\(N = 20\)
Entonces,
\(P_{20} = 3000 \left(1 + \dfrac{0.06}{12} \right)^{20 \times 12} = $9930.61\)(redondea tu respuesta al centavo más cercano)
Permítanos comparar la cantidad de dinero ganado por la capitalización con la cantidad que ganaría con intereses simples.
| Años | Interés Simple ($15 por mes) | 6% compuesto mensual = 0.5% cada mes. |
|---|---|---|
| 5 | $3900 | $4046.55 |
| 10 | $4800 | $5458.19 |
| 15 | $5700 | $7362.28 |
| 20 | $6600 | $9930.61 |
| 25 | $7500 | $13394.91 |
| 30 | $8400 | $18067.73 |
| 35 | $9300 | $24370.65 |
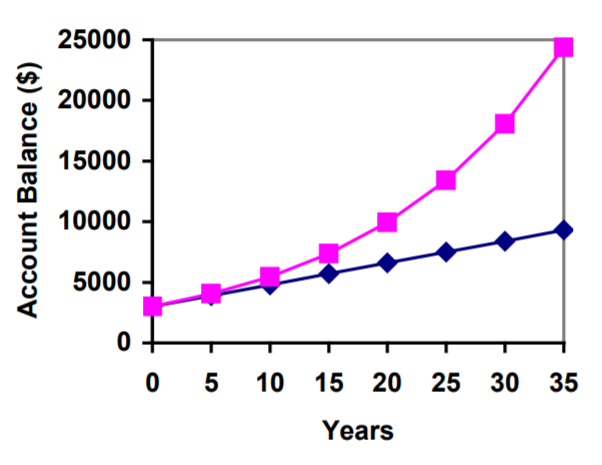
Como puede ver, durante un largo periodo de tiempo, la capitalización hace una gran diferencia en el saldo de la cuenta. Se puede reconocer esto como la diferencia entre el crecimiento lineal y el crecimiento exponencial.
Cuando necesitamos calcular algo así como\(5^3\) es bastante fácil de simplemente multiplicar\(5 \cdot 5 \cdot 5=125\). Pero cuando necesitamos calcular algo así\(1.0052^{40}\), ¡sería muy tedioso calcular esto multiplicando\(1.005\) por sí mismo los\(240\) tiempos! Entonces, para facilitar las cosas, podemos aprovechar el poder de nuestras calculadoras científicas.
La mayoría de las calculadoras científicas tienen un botón para exponentes. Por lo general, se etiqueta como:
\(^\),\(y^x\), o\(x^y\)
Para evaluar\(1.0052^{40}\) escribiríamos\(1.0052\)\(^\)\(40\), o\(1.0052\)\(y^x\)\(40\). Pruébalo - deberías conseguir algo alrededor\(3.3102044758\).
Sabes que necesitarás 40 mil dólares para la educación de tu hijo en 18 años. Si tu cuenta gana 4% compuesto trimestralmente, ¿cuánto necesitarías depositar ahora para alcanzar tu meta?
Solución
En este ejemplo, estamos buscando\(P_0\).
4%:
\(r = 0.04\)
4 trimestres en 1 año:
\(k = 4\)
Ya que conocemos el saldo en 18 años:
\(N = 18\)
La cantidad que tenemos en 18 años:
\(P_{18} = $40000\)
En este caso, vamos a tener que configurar la ecuación y resolver para\(P_0\).
\(40000 = P_0 \left(1 + \dfrac{0.04}{4} \right)^{18 \times 4}\)
\(40000 = P_0 \left( 2.0472 \right)\)
\(P_0 = \dfrac{40000}{2.0472} = $19539.84\)
Entonces, necesitarías depositar\($19,539.84\) ahora para tener\($40,000\) en\(18\) años.
Es importante tener mucho cuidado al redondear a la hora de calcular las cosas con exponentes. En general, quieres mantener tantos decimales durante los cálculos como puedas. Asegúrese de mantener al menos 3 dígitos significativos (números después de los ceros a la cabeza). Redondear 0.00012345 a 0.000123 generalmente te dará una respuesta “lo suficientemente cercana”, pero mantener más dígitos siempre es mejor.
La razón por la que no deberíamos “sobre-redondear” se muestra en este ejemplo. Supongamos que estuvo invirtiendo $1,000 al 5% de interés compuesto mensualmente por 30 años.
Solución
El depósito inicial:
\(P_0 = $1000\)
5%:
\(r = 0.05\)
12 meses en 1 año:
\(k = 12\)
Ya que estamos buscando la cantidad después de 30 años:
\(N = 30\)
Si primero calculamos\(\dfrac{r}{k}\), encontramos\(\dfrac{0.05}{12} = 0.00416666666667\)
Aquí está el efecto de redondear esto a diferentes valores:
| \(\dfrac{r}{k}\)redondeado a: | Da\(P_{30}\) a ser: | Error |
|---|---|---|
| \ (\ dfrac {r} {k}\) redondeado a: ">0.004 | \ (P_ {30}\) ser: ">$4208.59 | $259.15 |
| \ (\ dfrac {r} {k}\) redondeado a: ">0.0042 | \ (P_ {30}\) ser: ">$4521.45 | 53,71$ |
| \ (\ dfrac {r} {k}\) redondeado a: ">0.00417 | \ (P_ {30}\) a ser: ">$4473.09 | $5.35 |
| \ (\ dfrac {r} {k}\) redondeado a: ">0.004167 | \ (P_ {30}\) ser: ">$4468.28 | $0.54 |
| \ (\ dfrac {r} {k}\) redondeado a: ">0.0041667 | \ (P_ {30}\) a ser: ">$4467.80 | $0.06 |
| \ (\ dfrac {r} {k}\) redondeado a: ">Sin redondeo | \ (P_ {30}\) a ser: ">$4467.74 |
Si estás trabajando en un banco, claro que no redondearías en absoluto. Para nuestros propósitos, la respuesta que obtuvimos redondeando a\(0.00417\), tres dígitos significativos, está lo suficientemente cerca -\($5\) off of\($4,500\) no está tan mal. Desde luego, mantener ese cuarto decimal no habría lastimado.
Uso de tu calculadora En muchos casos, puedes evitar redondear completamente por la forma en que ingresas las cosas en tu calculadora. Por ejemplo, en el ejemplo anterior, necesitábamos calcular
\(P_{30} = 1000 \left(1 + \dfrac{0.05}{12} \right)^{12 \times 30}\)
Podemos calcular rápidamente\(12 \times 30 = 360\), dando\(P_{30} = 1000 \left(1 + \dfrac{0.05}{12} \right)^{360}\)
Ahora podemos usar la calculadora.
| Escriba Esto | La calculadora muestra |
|---|---|
| \(0.05\; ÷ \;12 \;= \) | 0.00416666666667 |
| \(+\; 1\; =\) | 1.00416666666667 |
| \(y^x\; 360\; = \) | 4.46774431400613 |
| \(\times \; 1000 \;=\) | 4467.74431400613 |
Los pasos anteriores eran suponer que tienes una calculadora de “una operación a la vez”; una calculadora más avanzada a menudo te permitirá escribir toda la expresión a evaluar. Si tienes una calculadora como esta, probablemente solo necesitarás ingresar:
\(1000 \; \times \; (1\; +\; 0.05\; ÷ \;12)\; y^x \;360\; =\)