1.6: Uso cuidadoso del lenguaje en matemáticas
( \newcommand{\kernel}{\mathrm{null}\,}\)
Esta sección puede parecer un poco desviada de la idea de resolver problemas, pero de hecho no lo es. La matemática es un esfuerzo social. No solo resolvemos problemas y luego los dejamos a un lado. La resolución de problemas tiene (al menos) tres componentes:
- Resolviendo el problema. Esto implica mucho papel rascar y pensar cuidadosamente.
- Convencerse de que su solución es completa y correcta. Esto implica mucho autochequeo y hacerse preguntas.
- Convencer a otra persona de que su solución es completa y correcta. Esto suele implicar escribir el problema con cuidado o explicar tu trabajo en una presentación.
Si no eres capaz de hacer ese último paso, entonces realmente no has resuelto el problema. Hablaremos más sobre cómo redactar una solución pronto. Antes de hacer eso, tenemos que pensar en cómo los matemáticos usan el lenguaje (que es, resulta, un poco diferente de cómo se usa el lenguaje en el resto de la vida).
Declaraciones matemáticas
Una declaración matemática es una oración completa que es verdadera o falsa, pero no ambas a la vez.
Entonces una “declaración” en matemáticas no puede ser una pregunta, un comando, o una cuestión de opinión. Es una oración completa, gramaticalmente correcta (con un sujeto, verbo y generalmente un objeto). Es importante que la afirmación sea verdadera o falsa, ¡aunque quizá no sepas cuál! (Parte del trabajo de un matemático es averiguar qué oraciones son verdaderas y cuáles son falsas).
Para cada frase en inglés a continuación, decide si es una declaración matemática o no. Si es así, ¿la afirmación es verdadera o falsa (o no está seguro)? Si no es una declaración matemática, ¿de qué manera falla?
- El azul es el color más bonito.
- 60 es un número par.
- ¿Tu perro es amigable?
- Honolulu es la capital de Hawái.
- Esta frase es falsa.
- Todas las rosas son rojas.
- UH Manoa es la mejor universidad del mundo.
- 1/2 = 2/4.
- Vete a la cama.
- Hay un total de 204 cuadrados en un tablero de ajedrez de 8 × 8.
Ahora escribe tres declaraciones matemáticas y tres oraciones en inglés que no logran ser declaraciones matemáticas.
Observe que “1/2 = 2/4” es una afirmación matemática perfectamente buena. No parece una frase en inglés, sino que la lee en voz alta. El tema es “1/2”. El verbo es “igual”. Y el objeto es “2/4”. Esta es una muy buena prueba cuando escribes matemáticas: intenta leerla en voz alta. Incluso las ecuaciones deberían leerse naturalmente, como las oraciones en inglés.
El enunciado (5) es diferente de los demás. Se le llama paradoja: una afirmación que es autocontradictoria. Si es cierto, entonces concluimos que es falso. (¿Por qué?) Si es falso, entonces concluimos que es cierto. (¿Por qué?) Las paradojas no sirven como afirmaciones matemáticas, porque no puede ser verdad y no puede ser falsa.
Y/o
Considera esta frase:
Después del trabajo, iré a la playa, o haré mis compras de comestibles.
En inglés cotidiano, eso probablemente signifique que si voy a la playa, no iré de compras. Voy a hacer una u otra, pero no ambas actividades. Esto se llama un “o exclusivo”.
Por lo general, podemos decir desde el contexto si un hablante significa “uno o el otro o ambos”, o si quiere decir “uno o el otro pero no ambos”. (Algunas personas usan la incómoda frase “y/o” para describir la primera opción).
Recuerda que en la comunicación matemática, sin embargo, tenemos que ser muy precisos. No podemos confiar en el contexto o en las suposiciones sobre lo que está implícito o entendido.
En matemáticas, la palabra “o” siempre significa “uno u otro o ambos”.
La palabra “y” siempre significa “ambos son verdaderos”.
Para cada oración a continuación:
- Decidir si la elección x = 3 hace que la declaración sea verdadera o falsa.
- Elegir un valor diferente de que haga que la afirmación sea verdadera (o decir por qué eso no es posible).
- Elegir un valor diferente de que haga que la declaración sea falsa (o decir por qué eso no es posible).
- x es impar o x es par.
- x es impar y x es par.
- x es primo o x impar.
- x > 5 o x < 5.
- x > 5 y x < 5.
- x + 1 = 7 o x — 1 = 7.
- x ·1 = x o x ·0 = x.
- x ·1 = x y x ·0 = x.
- x ·1 = x o x ·0 = 0.
Cuantificadores
Se le entrega un sobre lleno de dinero, y se le dice “Cada factura de este sobre es una factura de $100”.
- ¿Qué te convencería más allá de toda duda de que la sentencia es cierta? ¿Cómo podrías convencer a alguien más de que la sentencia es verdadera?
- ¿Qué te convencería más allá de toda duda de que la sentencia es falsa? ¿Cómo podrías convencer a alguien más de que la sentencia es falsa?
Supongamos que se le dio una frase diferente: “Hay un billete de 100 dólares en este sobre”.
- ¿Qué te convencería más allá de toda duda de que la sentencia es cierta? ¿Cómo podrías convencer a alguien más de que la sentencia es verdadera?
- ¿Qué te convencería más allá de toda duda de que la sentencia es falsa? ¿Cómo podrías convencer a alguien más de que la sentencia es falsa?
¿Cuál es la diferencia entre las dos frases? ¿Cómo afecta esa diferencia a tu método para decidir si la afirmación es verdadera o falsa?
Algunas declaraciones matemáticas tienen esta forma:
- “Cada vez...”
- “Para todos los números.”.
- “Para cada elección.”.
- “Siempre es cierto eso”.
Se trata de declaraciones universales. Tales afirmaciones afirman que algo siempre es cierto, pase lo que pase.
- Para probar que una afirmación universal es falsa, hay que encontrar un ejemplo donde falla. A esto se le llama contraejemplo a la declaración.
- Para probar que una afirmación universal es cierta, debes verificar cada caso individual, o debes encontrar una razón lógica por la que sería verdad. (A veces la primera opción es imposible, porque puede haber infinitamente muchos casos por verificar. ¡Nunca terminarías!)
Algunas declaraciones matemáticas tienen esta forma:
- “A veces...”
- “Hay algún número”.
- “Para alguna elección.”.
- “Al menos una vez...”
Se trata de declaraciones existenciales. Tales afirmaciones afirman que hay algún ejemplo donde la afirmación es verdadera, pero puede que no siempre sea cierta.
- Para probar que una afirmación existencial es cierta, es posible que solo encuentres el ejemplo donde funciona.
- Para probar que una afirmación existencial es falsa, debes o demostrar que falla en cada caso, o debes encontrar una razón lógica por la que no puede ser verdad. (¡A veces la primera opción es imposible!)
Para cada declaración a continuación, haga lo siguiente:
- Decidir si se trata de una declaración universal o de una declaración existencial. (Esto puede ser complicado porque en algunas declaraciones el cuantificador está “oculto” en el significado de las palabras).
- Decide si la declaración es verdadera o falsa, y haz todo lo posible para justificar tu decisión.
- Cada número impar es primo.
- Cada número primo es impar.
- Para todos los números positivosx,x3>x.
- Hay algún númerox tal quex3=x.
- Los puntos (1, 1), (2, 1) y (3, 0) se encuentran todos en la misma línea.
- La suma (de números reales) es conmutativa.
- La división (de números reales) es conmutativa.
Mira hacia atrás sobre tu trabajo. probablemente encontrarás que algunos de tus argumentos son sólidos y convincentes mientras que otros lo son menos. En algunos casos es posible que “conozca” la respuesta pero no pueda justificarla. ¡Eso está bien por ahora! Divide tus respuestas en cuatro categorías:
- Confío en que la justificación que di es buena.
- No confío en la justificación que di.
- Confío en que la justificación que di no es buena, o no podría dar una justificación.
- No pude decidir si la declaración era verdadera o falsa.
Declaraciones condicionales
Tienes una baraja de cartas donde cada carta tiene una letra en un lado y un número en el otro lado. Tu amigo afirma: “Si una tarjeta tiene una vocal en un lado, entonces tiene un número par en el otro lado”.
Estas tarjetas están sobre una mesa.
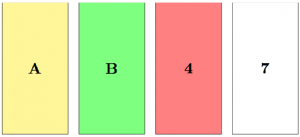
¿Qué cartas debes voltear para estar seguro de que tu amigo está diciendo la verdad?
Después de haber pensado en el problema por tu cuenta por un tiempo, discute tus ideas con un compañero. ¿Estás de acuerdo en qué tarjetas debes verificar? Trate de llegar a un acuerdo sobre una respuesta que ambos creen.
Aquí hay otro problema muy similar, sin embargo, la gente parece tener un tiempo más fácil resolviendo este:
Estás a cargo de una fiesta donde hay jóvenes. Algunos están bebiendo alcohol, otros refrescos. Algunos tienen la edad suficiente para beber alcohol legalmente, otros son menores de edad. Usted es responsable de asegurarse de que no se violen las leyes sobre el consumo de alcohol, por lo que ha pedido a cada persona que ponga su identificación con foto sobre la mesa. En una mesa, hay cuatro jóvenes:
- Una persona tiene una lata de cerveza, otra tiene una botella de Coca-Cola, pero sus identificaciones pasan a estar boca abajo por lo que no se pueden ver sus edades.
- Se pueden, sin embargo, ver las identificaciones de las otras dos personas. Uno es menor de la edad para beber, el otro está por encima de ella. Ambos tienen bebidas transparentes gaseosas en vasos, y no estás seguro de si están tomando agua de soda o gin-tonic.
¿Qué identificaciones y/o bebidas necesitas verificar para asegurarte de que nadie está infringiendo la ley?
Después de haber pensado en el problema por tu cuenta por un tiempo, discute tus ideas con un compañero. ¿Estás de acuerdo en qué tarjetas debes verificar? Compara estos dos problemas. ¿Qué pregunta es más fácil y por qué?
Una declaración condicional se puede escribir en la forma
Si alguna declaración entonces alguna declaración.
Donde el primer enunciado es la hipótesis y el segundo enunciado es la conclusión.
Estas son cada una de las declaraciones condicionales, aunque no todas están declaradas en forma “si/entonces”. Identificar la hipótesis de cada enunciado. (Es posible que desee reescribir la oración como una declaración equivalente “si/entonces”).
- Si los tomates son rojos, entonces están listos para comer.
Los tomates son rojos./Los tomates están listos para comer. - Un entero n es incluso si es un múltiplo de 2.
n es par./n es un múltiplo de 2. - Si n es impar, entonces n es primo.
n es impar. /n es primo. - El equipo gana cuando juega JJ.
El equipo gana./JJ juega.
Recuerde que una afirmación matemática debe tener un valor de verdad definido. Es verdadero o falso, sin área gris (aunque no estemos seguros de cuál es el caso). ¿Cómo se puede saber si una declaración condicional es verdadera o falsa? Seguramente, depende de si la hipótesis y la conclusión son verdaderas o falsas. Pero, ¿cómo, exactamente, puedes decidir?
La clave es pensar en una declaración condicional como una promesa, y preguntarse: ¿bajo qué condición (s) habré roto mi promesa?
Aquí hay una declaración condicional:
Si gano la lotería, entonces le daré a cada uno de mis alumnos $1,000.
Hay cuatro cosas que pueden suceder:
- Hipótesis verdadera, conclusión verdadera: Yo gano la lotería, y les doy a todos en clase $1,000. Cumplí mi promesa, por lo que la declaración condicional es VERDADERA.
- Cierta hipótesis, falsa conclusión: Yo gano la lotería, pero decido no dar a todos en clase mil dólares. Rompí mi promesa, por lo que la declaración condicional es FALSA.
- Falsa hipótesis, verdadera conclusión: Yo no gano la lotería, pero soy sumamente generosa, así que sigo adelante y les doy a todos en clase mil dólares. ¡No rompí mi promesa! (¿Ves por qué?) Entonces la declaración condicional es VERDADERA.
- Falsa hipótesis, falsa conclusión: Yo no gano la lotería, así que no le doy a todos en clase mil dólares. ¡No rompí mi promesa! (¿Ves por qué?) Entonces la declaración condicional es VERDADERA.
¿Qué podemos concluir de esto? Una declaración condicional es falsa sólo cuando la hipótesis es verdadera y la conclusión es falsa. En todos los demás casos, la promesa (por así decirlo) no se ha roto. Si una afirmación matemática no es falsa, debe ser cierta.
Aquí hay otra declaración condicional:
Si vives en Honolulu, entonces vives en Hawaii.
¿Esta afirmación es verdadera o falsa? Parece que debería depender de a quién se refiere el pronombre “tú”, y de si esa persona vive en Honolulu o no. Pensémoslo a través de:
- Sookim vive en Honolulu, por lo que la hipótesis es cierta. Desde que Honolulu está en Hawai, vive en Hawai. El enunciado es cierto sobre Sookim, ya que tanto la hipótesis como la conclusión son ciertas.
- DeeDee vive en Los Ángeles. La afirmación es cierta sobre DeeDee ya que la hipótesis es falsa.
Entonces, de hecho, ¡no importa! La afirmación es cierta de cualquier manera. La manera correcta de entender tal afirmación es como una declaración universal: “Todos los que viven en Honolulu viven en Hawai”.
Esta afirmación es cierta, y así es como podrías justificarla: “Elige a una persona al azar que viva en Honolulu. Esa persona vive en Hawai (ya que Honolulu está en Hawai), por lo que la afirmación es cierta para esa persona. No necesito considerar a las personas que no viven en Honolulu. El enunciado es automáticamente cierto para esas personas, ¡porque la hipótesis es falsa!”
¿Cómo mostramos que una declaración condicional (universal) es falsa?
Es necesario dar una instancia específica donde la hipótesis sea verdadera y la conclusión sea falsa. Por ejemplo:
Si eres un buen nadador, entonces eres un buen surfista.
¿Conoces a alguien para quien la hipótesis es cierta (esa persona es un buen nadador) pero la conclusión es falsa (la persona no es un buen surfista)? ¡Entonces la declaración es falsa!
Por cada declaración condicional, decida si es verdadera o falsa. Justifica tu respuesta.
- Si2×2=4 entonces1+1=3.
- Si2×2=5 entonces1+1=3.
- Siπ>3 entonces todos los números impares son primos.
- Siπ<3 entonces todos los números impares son primos.
- Si un número tiene un 4 en el lugar del uno, entonces el número es par.
- Si un número es par, entonces el número tiene un 4 en el lugar del uno.
- Si el producto de dos números es 0, entonces uno de los números es 0.
- Si la suma de dos números es 0, entonces uno de los números es 0.
Por su cuenta, llegar a dos declaraciones condicionales que sean verdaderas y una que sea falsa. Comparte tus tres afirmaciones con un compañero, pero no digas cuáles son verdaderas y cuáles son falsas. ¡Mira si tu pareja puede resolverlo!

