Saltar al contenido principal
LibreTexts Español

6.10: Banco de Problemas

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    112811

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Problema 28

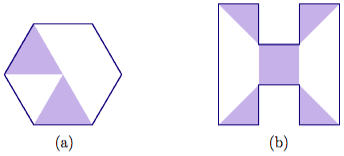
    Exprese la porción sombreada de cada figura tanto como fracción como decimal. Justifica tus respuestas.

    problem17.png

    Problema 29

    ¿Qué número es mayor: 0.135 o 0.14? Justifica tu respuesta.

    Problema 30

    Organice los dígitos 1, 2, 3 y 4 en las casillas para crear la suma más pequeña posible. Usa cada dígito exactamente una vez. Justifica que tu respuesta sea lo más pequeña posible.

    \[\frac{\Box}{\Box} + \frac{\Box}{\Box} \nonumber \]

    Problema 31

    Organice los dígitos 1, 2, 3 y 4 en las casillas para crear la menor diferencia posible (positiva). Usa cada dígito exactamente una vez. Justifica que tu respuesta sea lo más pequeña posible.

    \[\frac{\Box}{\Box} - \frac{\Box}{\Box} \nonumber \]

    Problema 32

    Usa el modelo “Dots & Boxes” para mostrar eso\(\frac{1}{9} = 0. \bar{1}\). Entonces usa este hecho para responder a estas preguntas y justificar tus respuestas.

    1. ¿Qué fracción viene dada por\(0. \bar{2}\)?
    2. ¿Qué fracción viene dada por\(0. \bar{5}\)?
    3. ¿Qué fracción viene dada por\(0. \bar{6}\)?
    4. ¿Qué fracción viene dada por\(0. \bar{8}\)?
    5. ¿Qué fracción viene dada por\(0. \bar{9}\)?

    Problema 33

    En este problema, te enfocarás en el cálculo

    \[170 \times \Box \ldotp \nonumber \]

    Tu objetivo es conseguir un producto que esté cerca de 200.

    1. ¿Multiplicarás 170 por un número mayor o menor que 1? ¿Mayor o menor que 2? Justifica tus respuestas.
    2. Supongamos que puede usar solo una posición decimal. Rellena la casilla con un número que se acerque lo más posible a 200.
    3. Supongamos que solo puedes usar dos decimales. Rellena la casilla con un número que se acerque lo más posible a 200.
    4. Supongamos que solo puedes usar tres decimales. Rellena la casilla con un número que se acerque lo más posible a 200.

    Problema 34

    Haga cada cálculo a continuación sin usar una calculadora. Explica tu pensamiento.

    1. $$ (23\ times 0.1) + (0.001\ times 55)\ ldotp$$
    2. $$18.45\ div (0.63\ div 0.7)\ ldotp$$
    3. $$22.65 - (0.03\ cdot 10)\ ldotp$$

    Problema 35

    Sin realmente calcular nada (¡solo usa tu sentido numérico!) , ordene x, y y z de menor a mayor. Explique su pedido.

    \[\begin{split} x &= 0.07 + 0.000001 \\ y &= 0.07 \times 0.000001 \\ z &= 0.07 \div 0.000001 \end{split} \nonumber \]

    Problema 36

    Para cada pregunta a continuación, elija el cálculo correcto y explique su elección. Después estime la respuesta (no la calcule exactamente) y explique por qué su estimación es buena.

    1. Una pizza grande tiene ocho rebanadas y cuesta $15.95. ¿Cuánto cuesta cada porción de pizza? ¿Deberías calcular 15.95 × 8 o 15.95 ÷ 8?
    2. Hay 2.54 centímetros en una pulgada. Una hoja estándar de papel para cuaderno mide\(8 \frac{1}{2}\) pulgadas de ancho y 11 pulgadas de largo. ¿Cuántos centímetros de ancho tiene la página? ¿Debe calcular 8.5 × 2.54 o 11 × 2.54 o 8.5 ÷ 2.54 o 11 ÷ 2.54?
    3. En un juego de tren modelo, 1.38 pulgadas representa un pie en la vida real. La altura del One World Trade Center en la ciudad de Nueva York es de 1776 pies. ¿Qué tan alto sería una maqueta del edificio? ¿Debería calcular 1776 × 1.38 o 1776 ÷ 1.38?
    4. Ocho décimas de un jumprope mide 1.75 metros de largo. ¿Cuánto dura toda la cuerda? ¿Debe calcular 0.8 × 1.75 o 0.8 ÷ 1.75 o 1.75 ÷ 0.8?

    Problema 37

    Kaimi no tenía nada de dinero cuando cobró su cheque de pago. Al salir de la orilla, compró una pieza de caramelo por una moneda de cinco centavos de una máquina. Posteriormente, se dio cuenta de que el dinero en su bolsillo equivalía al doble de su sueldo. Después de un cálculo rápido, se dio cuenta de lo que pasó: el cajero cambió accidentalmente los dólares y centavos. ¿Cuánto se suponía que debía pagar a Kaimi y qué le dio el cajero? Justifica tu respuesta.

    Problema 38

    Aquí están las reglas para un juego de cartas. Lea las reglas cuidadosamente y luego responda las preguntas a continuación.

    • Cada jugador comienza con 10 puntos. El objetivo es anotar lo más cerca posible de los 100 puntos sin rebasar.
    • En tu turno: saca dos cartas, cada una de las cuales tendrá un número decimal sobre ellas. Usando estimación (sin cálculo), puedes elegir multiplicar o dividir tu puntaje actual por uno de los números decimales.
    • Después de decidir, calcule su nueva puntuación exactamente usando una calculadora. Si tu nueva puntuación supera los 100, pierdes. Si no, el otro jugador toma un turno.
    • Al final de tu turno, podrás decidir terminar el juego. Si lo haces, el otro jugador obtiene un turno más. Entonces, el jugador con la puntuación más cercana a 100 sin rebasar gana el juego.

    Aquí están las preguntas:

    1. En tu turno, tu puntuación es de 50. Se robas las cartas 0.2 y 1.75. Recuerda que tus opciones son: $$\ begin {split} &\ text {divide por}\; 0.2\ qquad\ text {multiplicar por}\; 0.2\\ &\ text {divide por}\; 1.75\ qquad\ text {multiplicar por}\; 1.75\ ldotp\ end {split} $$ ¿Cuál es tu mejor jugada y por qué?
    2. En tu turno, tu puntuación es de 88. Se dibuja 1.3 y 0.6. ¿Cuál es tu mejor jugada y por qué?
    3. Tu pareja tiene una puntuación de 57, y tu puntuación es 89. En su turno, tu pareja dibuja 0.8 y 1.8. Dice que quiere terminar el juego. En tu turno final, empatas 0.7 y 1.2. Si ambos hacen la mejor jugada posible, ¿quién ganará el juego? Justifica tu respuesta.

    This page titled 6.10: Banco de Problemas is shared under a CC BY-SA 4.0 license and was authored, remixed, and/or curated by Michelle Manes via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.