11.4: Resolviendo Ecuaciones de la Forma ax = b y x/a = b

Última actualización
Guardar como PDF

Page ID: 116353

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

Objetivos de aprendizaje

estar familiarizado con la propiedad de multiplicación/división de la igualdad
ser capaz de resolver ecuaciones de la forma$ax = b$ y$\dfrac{x}{a} = b$
ser capaz de utilizar técnicas combinadas para resolver ecuaciones

Multiplicación/ División Propiedad de Igualdad

Recordemos que el signo igual de una ecuación indica que el número representado por la expresión en el lado izquierdo es el mismo que el número representado por la expresión en el lado derecho. A partir de esto, podemos sugerir la propiedad de multiplicación/división de la igualdad.

Multiplicación/División Propiedad de la Igualdad
Dada cualquier ecuación,

Podemos obtener una ecuación equivalente multiplicando ambos lados de la ecuación por el mismo número distinto de cero, es decir, if$c \ne 0$. then$a = b$ es equivalente a
$a \cdot c = b \cdot c$
Podemos obtener una ecuación equivalente dividiendo ambos lados de la ecuación por el mismo número distinto de cero, es decir, si$c \ne 0$, entonces$a = b$ es equivalente a
$\dfrac{a}{c} = \dfrac{b}{c}$

La propiedad multiplicación/división de igualdad se puede utilizar para deshacer una asociación con un número que multiplica o divide la variable.

Conjunto de Muestras A

Utilice la propiedad multiplicación/división de la igualdad para resolver cada ecuación.

$6y = 54$

Solución

6 se asocia con y por multiplicación. Deshacer la asociación dividiendo ambos lados por 6

$\begin{array} {rcl} {\dfrac{6y}{6}} & = & {\dfrac{54}{6}} \\ {\dfrac{\cancel{6} y}{\cancel{6}}} & = & {\dfrac{\begin{array} {c} {^9} \\ {\cancel{54}} \end{array}}{\cancel{6}}} \\ {y} & = & {9} \end{array}$

Comprobar: Cuándo$y = 9$

$6y = 54$

se convierte

$¿6 veces 9 es igual a 54? Sí.$

una declaración verdadera.

La solución a$6y = 54$ es$y = 9$.

Conjunto de Muestras A

$\dfrac{x}{-2} = 27$.

Solución

-2 está asociado con$x$ por división. Deshacer la asociación multiplicando ambos lados por -2.

$(-2) \dfrac{x}{-2} = (-2) 27$

$(\cancel{-2}) \dfrac{x}{\cancel{-2}} = (-2) 27$

$x = -54$

Comprobar: Cuándo$x = -54$.

$\dfrac{x}{-2} = 27$

se convierte

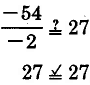
$¿El negativo 54 sobre el 2 negativo es igual a 27? Sí.$

una declaración verdadera.

La solución$\dfrac{x}{-2} = 27$ es$x = -54$

Conjunto de Muestras A

$\dfrac{3a}{7} = 6$.

Solución

Examinaremos dos métodos para resolver ecuaciones como esta.

Método 1: Uso de dividir factores comunes.

$\dfrac{3a}{7} = 6$

7 está asociado con$a$ por división. Deshacer la asociación multiplicando ambas partes por 7.

$7 \cdot \dfrac{3a}{7} = 7 \cdot 6$

Dividir los 7's

$\cancel{7} \cdot \dfrac{3a}{\cancel{7}} = 42$

$3a = 42$

3 se asocia con$a$ por multiplicación. Deshacer la asociación dviding ambas partes por 3.

$\dfrac{3a}{3} = \dfrac{42}{3}$

$\dfrac{\cancel{3} a}{\cancel{3}} = 14$

$a = 14$

Comprobar: Cuándo$a = 14$.

$\dfrac{3a}{7} = 6$

se convierte

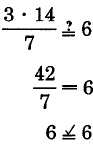
$¿La cantidad 3 por 14, dividida por 7 es igual a 6? Sí.$

una declaración verdadera.

La solución a$\dfrac{3a}{7} = 6$ es$a = 14$.

Método 2: Uso de reciprocales

Recordemos que si el producto de dos números es 1, los números son recíprocos. Así$\dfrac{3}{7}$ y$\dfrac{7}{3}$ son recíprocos.

$\dfrac{3a}{7} = 6$

Multiplique ambos lados de la ecuación por$\dfrac{7}{3}$, el recíproco de$\dfrac{3}{7}$.

$\dfrac{7}{3} \cdot \dfrac{3a}{7} = \dfrac{7}{3} \cdot 6$

$\dfrac{\begin{array} {c} {^1} \\ {\cancel{7}} \end{array}}{\begin{array} {c} {\cancel{3}} \\ {^1} \end{array}} \cdot \dfrac{\begin{array} {c} {^1} \\ {\cancel{3} a} \end{array}}{\begin{array} {c} {\cancel{7}} \\ {^1} \end{array}} = \dfrac{7}{\begin{array} {c} {\cancel{3}} \\ {^1} \end{array}} \cdot \dfrac{\begin{array} {c} {^2} \\ {\cancel{6}} \end{array}}{1}$

$1 \cdot a = 14$

$a = 14$

Observe que obtenemos la misma solución usando cualquiera de los dos métodos.

Conjunto de Muestras A

$-8x = 24$.

Solución

-8 se asocia con$x$ por multiplicación. Deshacer la asociación dividiendo ambos lados por -8.

$\dfrac{-8x}{-8} = \dfrac{24}{-8}$

$x = -3$

Comprobar: Cuándo$x = -3$.

$-8x = 24$

se convierte

$¿El negativo 8 veces negativo 3 es igual a 24? Sí.$

una declaración verdadera.

Conjunto de Muestras A

$-x = 7$.

Solución

Ya que$-x$ es en realidad$-1 \cdot x$ y$(-1)(-1) = 1$. Podemos aislar$x$ multiplicando ambos lados de la ecuación por -1.

$(-1)(-x) = -1 \cdot 7$.

$x = -7$

Comprobar: Cuándo$x= 7$.

$-x = 7$

se convierte

La solución a$-x = 7$ es$x = -7$.

Conjunto de práctica A

Utilice la propiedad de multiplicación/división de la igualdad para resolver cada ecuación. Asegúrese de verificar cada solución.

$7x = 21$

Responder: $x = 3$

Conjunto de práctica A

$-5x = 65$

Responder: $x = -13$

Conjunto de práctica A

$\dfrac{x}{4} = -8$

Responder: $x = -32$

Conjunto de práctica A

$\dfrac{3x}{8} = 6$

Responder: $x = 16$

Conjunto de práctica A

$-y = 3$

Responder: $y = -3$

Conjunto de práctica A

$-k = -2$

Responder: $k = 2$

Combinar técnicas en la resolución de ecuaciones

Habiendo examinado la resolución de ecuaciones utilizando los principios de sución/resta y multiplicación/división de igualdad, podemos combinar estas técnicas para resolver ecuaciones más complicadas.

Al comenzar a resolver una ecuación como$6x - 4 = -16$, es útil saber qué propiedad de igualdad usar primero, sución/resta o multiplicación/división. Recordando que en la resolución de ecuaciones estamos tratando de aislar la variable (desasociar números de ella), es útil señalar lo siguiente.

Para asociar números y letras, utilizamos el orden de las operaciones.

Multiplicar/dividir
Añadir/restar

Para deshacer una asociación entre números y letras, utilizamos el orden de las operaciones a la inversa.

Añadir/restar
Multiplicar/dividir

Conjunto de Muestras B

Resuelve cada ecuación. (En estos problemas de ejemplo, no vamos a mostrar los cheques.)

$6x - 4 = -16$

Solución

-4 se asocia con xx por resta. Deshacer la asociación agregando 4 a ambos lados.

$6x - 4 + 4 = -16 + 4$

$6x = -12$

6 se asocia con$x$ por multiplicación. Deshacer la asociación dividiendo ambos lados por 6

$\dfrac{6x}{6} = \dfrac{-12}{6}$

$x = -2$

Conjunto de Muestras B

$-8k + 3 = -45$

Solución

3 se asocia con$k$ por adición. Deshacer la asociación restando 3 de ambos lados.

$-8k + 3 - 3 = -45 - 3$

$-8k = -48$

-8 se asocia con$k$ por multiplicación. Deshacer la asociación dividiendo ambos lados por -8.

$\dfrac{-8k}{-8} = \dfrac{-48}{-8}$

$k = 6$

Conjunto de Muestras B

$5m - 6 - 4m = 4m - 8 + 3m$.

Solución

Comience por resolver esta ecuación combinando términos similares.

$m - 6 = 7m - 8$Elija un lado en el que aislar m. Dado que 7 es mayor que 1, aislaremos m en el lado derecho.
Restar m de ambos lados.

$-m - 6 - m = 7m - 8 - m$

$-6 = 6m - 8$

8 se asocia con m por resta. Deshacer la asociación agregando 8 a ambos lados.

$-6 + 8 = 6m - 8 + 8$

$2 = 6m$

6 se asocia con m por multiplicación. Deshacer la asociación dividiendo ambos lados por 6.

$\dfrac{2}{6} = \dfrac{6m}{6}$Reducir,

$\dfrac{1}{3} = m$

Observe que si hubiéramos optado por aislar m en el lado izquierdo de la ecuación en lugar del lado derecho, habríamos procedido de la siguiente manera:

$m - 6 = 7m - 8$

Restar$7m$ de ambos lados.

$m - 6 - 7m = 7m - 8 - 7m$

$-6m - 6 = -8$

Añadir 6 a ambos lados,

$-6m - 6 + 6 = -8 + 6$

$-6m = -2$

Divide ambos lados por -6.

$\dfrac{-6m}{-6} = \dfrac{-2}{-6}$

$m = \dfrac{1}{3}$

Este es el mismo resultado que con el enfoque anterior.

Conjunto de Muestras B

$\dfrac{8x}{7} = -2$

Solución

7 está asociado con$x$ por división. Deshacer la asociación multiplicando ambas partes por 7.

$\cancel{7} \cdot \dfrac{8x}{\cancel{7}} = 7(-2)$

$7 \cdot \dfrac{8x}{7} = -14$

$8x = -14$

8 se asocia con$x$ por multiplicación. Deshacer la asociación dividiendo ambos lados por 8.

$\dfrac{\cancel{8} x}{\cancel{8}} = \dfrac{-7}{4}$

$x = \dfrac{-7}{4}$

Set de práctica B

Resuelve cada ecuación. Asegúrese de verificar cada solución.

$5m + 7 = -13$

Responder: $m = -4$

Set de práctica B

$-3a - 6 = 9$

Responder: $a = -5$

Set de práctica B

$2a + 10 - 3a = 9$

Responder: $a = 1$

Set de práctica B

$11x - 4 - 13x = 4x + 14$

Responder: $x = -3$

Set de práctica B

$-3m + 8 = -5m + 1$

Responder: $m = -\dfrac{7}{2}$

Set de práctica B

$5y + 8y - 11 = -11$

Responder: $y = 0$

Ejercicios

Resuelve cada ecuación. Asegúrese de verificar cada resultado.

Ejercicio$\PageIndex{1}$

$7x = 42$

Responder: $x = 6$

Ejercicio$\PageIndex{2}$

$8x = 81$

Ejercicio$\PageIndex{3}$

$10 x = 120$

Responder: $x = 12$

Ejercicio$\PageIndex{4}$

$11 x = 121$

Ejercicio$\PageIndex{5}$

$-6a = 48$

Responder: $a = -8$

Ejercicio$\PageIndex{6}$

$-9y = 54$

Ejercicio$\PageIndex{7}$

$-3y = -42$

Responder: $y = 14$

Ejercicio$\PageIndex{8}$

$-5a = -105$

Ejercicio$\PageIndex{9}$

$2m = -62$

Responder: $m = -31$

Ejercicio$\PageIndex{10}$

$3m = -54$

Ejercicio$\PageIndex{11}$

$\dfrac{x}{4} = 7$

Responder: $x = 28$

Ejercicio$\PageIndex{12}$

$\dfrac{y}{3} = 11$

Ejercicio$\PageIndex{13}$

$\dfrac{-z}{6} = -14$

Responder: $z = 84$

Ejercicio$\PageIndex{14}$

$\dfrac{-w}{5} = 1$

Ejercicio$\PageIndex{1}$

$3m - 1 = -13$

Responder: $m = -4$

Ejercicio$\PageIndex{15}$

$4x + 7 = -17$

Ejercicio$\PageIndex{1}$

$2 + 9x = -7$

Responder: $x = -1$

Ejercicio$\PageIndex{16}$

$5 - 11x = 27$

Ejercicio$\PageIndex{17}$

$32 = 4y + 6$

Responder: $y = \dfrac{13}{2}$

Ejercicio$\PageIndex{18}$

$-5 + 4 = -8m + 1$

Ejercicio$\PageIndex{19}$

$3k + 6 = 5k + 10$

Responder: $k = -2$

Ejercicio$\PageIndex{20}$

$4a + 16 = 6a + 8a + 6$

Ejercicio$\PageIndex{21}$

$6x + 5 + 2x - 1 = 9x - 3x + 15$

Responder: $x = \dfrac{11}{2}$o$5 \dfrac{1}{2}$

Ejercicio$\PageIndex{22}$

$-9y - 8 + 3y + 7 = -7y + 8y - 5y + 9$

Ejercicio$\PageIndex{23}$

$-3a = a + 5$

Responder: \ (a = -\ dfrac {5} {4})

Ejercicio$\PageIndex{24}$

$5b = -2b + 8b + 1$

Ejercicio$\PageIndex{25}$

$-3m + 2 - 8m - 4 = -14m + m - 4$

Responder: $m = -1$

Ejercicio$\PageIndex{26}$

$5a + 3 = 3$

Ejercicio$\PageIndex{27}$

$7x + 3x = 0$

Responder: $x = 0$

Ejercicio$\PageIndex{28}$

$7g + 4 - 11g = -4g + 1 + g$

Ejercicio$\PageIndex{29}$

$\dfrac{5a}{7} = 10$

Responder: $a = 14$

Ejercicio$\PageIndex{30}$

$\dfrac{2m}{9} = 4$

Ejercicio$\PageIndex{31}$

$\dfrac{3x}{4} = \dfrac{9}{2}$

Contestar: $x = 6$

Ejercicio$\PageIndex{32}$

$\dfrac{8k}{3} = 32$

Ejercicio$\PageIndex{33}$

$\dfrac{3a}{8} - \dfrac{3}{2} = 0$

Contestar: $a = 4$

Ejercicio$\PageIndex{34}$

$\dfrac{5m}{6} - \dfrac{25}{3} = 0$

Ejercicios para la revisión

Ejercicio$\PageIndex{35}$

Usar la propiedad distributiva para calcular$40 \cdot 28$

Contestar: $40(30 - 2) = 1200 - 80 = 1120$

Ejercicio$\PageIndex{36}$

Aproximando$\pi$ por 3.14, encuentra la circunferencia aproximada del círculo.

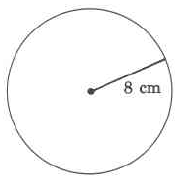
$Un círculo con radio de 8cm.$

Ejercicio$\PageIndex{37}$

Encuentra el área del paralelogramo.

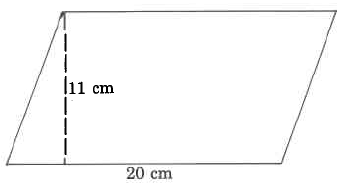
$Un paralelogramo con base 20cm y altura 11cm.$

Contestar: 220 cm cuadrados

Ejercicio$\PageIndex{38}$

Encuentra el valor de$\dfrac{-3(4 - 15) - 2}{-5}$

Ejercicio$\PageIndex{39}$

Resuelve la ecuación$x - 14 + 8 = -2$.

Contestar: $x = 4$