2.2: Sumando enteros

Última actualización
Guardar como PDF

Page ID: 113445

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Al igual que nuestro trabajo con los números enteros, la adición de enteros se explica mejor a través del uso de diagramas de líneas numéricas. Sin embargo, antes de comenzar, tomemos un momento para discutir el concepto de vector.

Vectores

Un vector es un objeto matemático que posee dos cualidades de importación: (1) magnitud o longitud, y (2) directon.

Los vectores son una herramienta fundamental para resolver problemas en matemáticas, ciencias e ingeniería. En física, los vectores se utilizan para representar fuerzas, posición, velocidad y aceleración, mientras que los ingenieros utilizan vectores para representar fuerzas internas y externas en estructuras, como puentes y edificios. En este curso, y en esta sección en particular, nos concentraremos en el uso de vectores para ayudar a explicar la adición de enteros.

Vectores en la Línea Numérica

Considera la recta numérica en la Figura$\PageIndex{1}$.

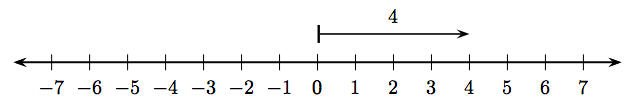
Screen Shot 2019-08-13 a las 8.51.19 PM.png — Figura$\PageIndex{1}$: Un vector que representa cuatro positivos.

Por encima de la línea hemos dibujado un vector con cola comenzando en el entero 0 y punta de flecha terminando en el entero 4. Hay dos cosas importantes a tener en cuenta sobre este vector:

La magnitud (longitud) del vector en la Figura$\PageIndex{1}$ es cuatro.
El vector en la Figura$\PageIndex{1}$ apunta a la derecha.

Estaremos de acuerdo en que el vector en la Figura$\PageIndex{1}$ representa cuatro positivos. No es importante que el vector comience en el origen. Consideremos, por ejemplo, el vector que se muestra en la Figura$\PageIndex{2}$.

Screen Shot 2019-08-13 a las 8.52.57 PM.png — Figura$\PageIndex{2}$: Un vector que representa cuatro positivos.

Nuevamente, hay que hacer dos observaciones importantes:

La magnitud (longitud) del vector en la Figura$\PageIndex{2}$ es cuatro.
El vector en la Figura$\PageIndex{2}$ apunta a la derecha.

Ojalá tengas la idea. Cualquier vector que tenga longitud 4 y puntos a la derecha representará cuatro positivos, independientemente de su punto inicial o final. Por el contrario, considere el vector en la Figura$\PageIndex{3}$, que comienza en el entero 4 y termina en el entero −3.

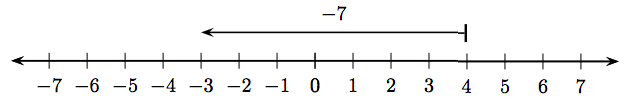
Screen Shot 2019-08-13 a las 8.53.51 PM.png — Figura$\PageIndex{3}$: Un vector que representa siete negativos.

Dos observaciones:

La magnitud (longitud) del vector en la Figura$\PageIndex{3}$ es siete.
El vector en la Figura$\PageIndex{3}$ apunta a la izquierda.

Estaremos de acuerdo en que el vector en la Figura$\PageIndex{3}$ representa siete negativos. Podríamos seleccionar diferentes puntos de inicio y finalización para nuestro vector, pero siempre y cuando el vector tenga longitud siete y puntos a la izquierda, representa el entero −7.

Observación Importante

Un vector que apunta a la derecha representa un número positivo. Un vector que apunta a la izquierda representa un número negativo.

Magnitud y Valor Absoluto

En Figura$\PageIndex{1}$ y Figura$\PageIndex{2}$, los vectores representados representan el entero positivo cuatro. Obsérvese que el valor absoluto de cuatro es cuatro; es decir, |4| = 4. Obsérvese también que este valor absoluto es la magnitud o longitud de los vectores que representan el entero positivo cuatro en la Figura$\PageIndex{1}$ y la Figura$\PageIndex{2}$.

En la Figura$\PageIndex{3}$, el vector representado representa el entero −7. Tenga en cuenta que | − 7| = 7. Esto demuestra que el valor absoluto representa la magnitud o longitud del vector que representa −7.

Magnitud y Valor Absoluto

Si a es un entero, entonces | a | da la magnitud o longitud del vector que representa el entero a.

Agregar números enteros con signos similares

Debido a que los enteros positivos también son números enteros, ya hemos visto cómo agregarlos en la Sección 1.2.

Ejemplo 1

Encuentra la suma 3 + 4.

Solución

Para sumar los enteros positivos 3 y 4, proceda de la siguiente manera.

Comienza en el entero 0, luego dibuja un vector de 3 unidades de longitud apuntando a la derecha, como se muestra en la Figura$\PageIndex{4}$. Esta flecha tiene magnitud (longitud) tres y representa el entero positivo 3.
Dibuja un segundo vector de longitud cuatro que apunte a la derecha, comenzando por el final del primer vector que representa el entero positivo 3. Esta flecha tiene magnitud (longitud) cuatro y representa el entero positivo 4.
La suma de los enteros positivos 3 y 4 podría estar representada por un vector que comienza en el entero 0 y termina en el entero positivo 7. Sin embargo, preferimos marcar esta suma en la recta numérica como un punto sólido en el entero positivo 7. Este entero representa la suma de los enteros positivos 3 y 4.

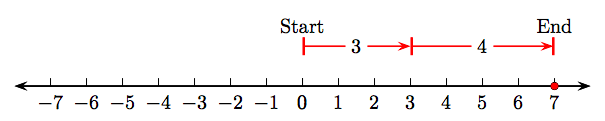
Screen Shot 2019-08-13 a las 8.57.49 PM.png — Figura$\PageIndex{4}$: Sumando dos enteros positivos en la recta numérica.

Así, 3 + 4 = 7

Ejercicio

Utilice un diagrama de líneas numéricos para mostrar la suma 5 + 7.

Contestar: 12

Los enteros negativos se agregan de manera similar.

Ejemplo 2

Encuentra la suma −3+ (−4).

Solución

Para sumar los números enteros negativos −3 y −4, proceda de la siguiente manera.

Comienza en el entero 0, luego dibuja un vector de 3 unidades de longitud apuntando a la izquierda, como se muestra en la Figura$\PageIndex{5}$. Esta flecha tiene magnitud (longitud) tres y representa el entero negativo −3.
Dibuja un segundo vector de longitud cuatro que apunte a la izquierda, comenzando por el final del primer vector que representa el entero negativo −3. Esta flecha tiene magnitud (longitud) cuatro y representa el entero negativo −4.
La suma de los números enteros negativos −3 y −4 podría representarse por un vector que comienza en el entero 0 y termina en el entero negativo −7. Sin embargo, preferimos marcar esta suma en la recta numérica como un punto sólido en el entero negativo −7. Este número entero representa la suma de los números enteros negativos −3 y −4.

Screen Shot 2019-08-13 a las 8.59.54 PM.png — Figura$\PageIndex{5}$: Sumando dos enteros positivos en la recta numérica.

Así, −3+ (−4) = −7.

Dibujo a partir de la intuición física. Imagina que estás “caminando por la recta numérica” en la Figura$\PageIndex{5}$. Empiezas en el origen (cero) y tomas 3 pasos a la izquierda. A continuación, caminas cuatro pasos adicionales hacia la izquierda, aterrizando en el número −7

Ejercicio

Utilice un diagrama de líneas numéricos para mostrar la suma −7+ (−3).

Contestar: −10

No debería sorprendernos que el procedimiento utilizado para sumar dos enteros negativos comprende dos pasos.

Sumando dos enteros negativos

Para sumar dos enteros negativos, proceda de la siguiente manera:

Suma las magnitudes de los enteros.
Prefijo el signo negativo común

Ejemplo 3

Encuentra las sumas: (a) −4+ (−5), (b) −12 + (−9) y (c) −2+ (−16).

Solución

Examinaremos tres enfoques separados pero equivalentes, como se discutió en la narrativa anterior.

a) El esquema de las líneas numéricas

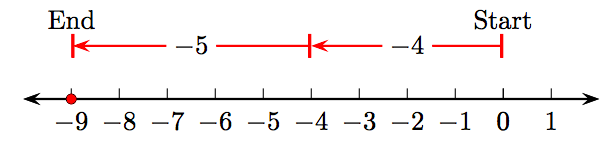
$Screen Shot 2019-08-14 at 9.32.52 AM.png$

muestra que (−4) + (−5) = −9.

b) Basándose en la intuición física, comenzar en cero, caminar 12 unidades hacia la izquierda, luego 9 unidades adicionales a la izquierda. Deberías encontrarte 21 unidades a la izquierda del origen (cero). De ahí que −12 + (−9) = −21.

c) Siguiendo el algoritmo anterior en “Sumando dos enteros negativos”, primero agregue las magnitudes de −2 y −16; es decir, 2+16 = 18. Ahora prefiera el signo común. Por lo tanto, −2+ (−16) = −18.

Ejercicio

Encuentra la suma: −5+ (−9).

Contestar: −14

Agregar números enteros con signos diferentes

Agregar enteros con signos diferentes no es más difícil que agregar enteros con signos similares.

Ejemplo 4

Encuentra la suma −8 + 4.

Solución

Para encontrar la suma −8 + 4, proceda de la siguiente manera:

Comienza en el entero 0, luego dibuja un vector de ocho unidades de longitud apuntando a la izquierda, como se muestra en la Figura$\PageIndex{6}$. Esta flecha tiene magnitud (longitud) ocho y representa el entero negativo −8.
Dibuja un segundo vector de longitud cuatro que apunte a la derecha, comenzando por el final del primer vector que representa el entero negativo −8. Esta flecha (también mostrada en la Figura$\PageIndex{6}$) tiene magnitud (longitud) cuatro y representa el entero positivo 4.
La suma de los números enteros negativos −8 y 4 podría representarse por un vector que comienza en el entero 0 y termina en el entero negativo −4. Sin embargo, preferimos marcar esta suma en la recta numérica como un punto sólido en el entero negativo −4. Este número entero representa la suma de los números enteros −8 y 4.

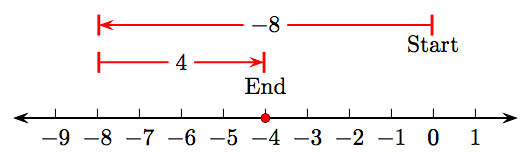
Screen Shot 2019-08-14 a las 9.38.02 AM.png — Figura$\PageIndex{6}$: Sumando −8 y 4 en la recta numérica.

Así, −8+4= −4.

Dibujo a partir de la intuición física. Imagina que estás “caminando por la recta numérica en la Figura$\PageIndex{6}$. Empiezas en el origen (cero) y caminas ocho pasos hacia la izquierda. A continuación, dar la vuelta y caminar cuatro pasos a la derecha, aterrizando sobre el número −4.

Ejercicio

Utilice un diagrama de líneas numéricos para mostrar la suma −9 + 2.

Contestar: −7

Tenga en cuenta que sumar enteros con signos diferentes es un proceso sustractivo. Esto se debe a la inversión de dirección experimentada en el dibujo de la Figura$\PageIndex{6}$ en el Ejemplo 4.

Agregar dos enteros con signos diferentes

Para agregar dos enteros con signos diferentes, proceda de la siguiente manera:

Restar la magnitud menor de la magnitud mayor.
Prefije el signo del número con la magnitud mayor.

Por ejemplo, para encontrar la suma −8 + 4 del Ejemplo 4, notaríamos que los enteros −8 y 4 tienen magnitudes 8 y 4, respectivamente. Entonces aplicaríamos el proceso descrito en “Agregar dos enteros con signos diferentes”.

Restar la magnitud menor de la magnitud mayor; es decir, 8 − 4 = 4.
Prefije el signo del número con la magnitud mayor. Debido a que −8 tiene la magnitud mayor y su signo es negativo, predecimos un signo negativo a la diferencia de las magnitudes. Así, −8+4= −4.

Ejemplo 5

Encuentra las sumas: (a) 5+ (−8), (b) −12+ 16, y (c) −117+115.

Solución

Examinaremos tres enfoques separados pero equivalentes, como se discutió en la narrativa anterior.

a) El esquema de las líneas numéricas

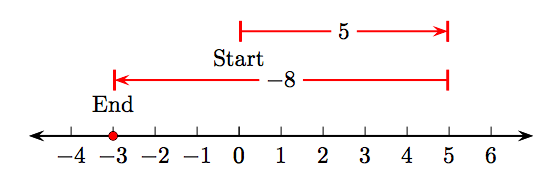
$Screen Shot 2019-08-14 a las 9.44.03 AM.png$

muestra que 5 + (−8) = −3.

b) Basándose en la intuición física, comenzar en cero, caminar 12 unidades a la izquierda, luego dar la vuelta y caminar 16 unidades a la derecha. Deberías encontrarte 4 unidades a la derecha del origen (cero). De ahí que −12 + 16 = 4.

c) Siguiendo el algoritmo en “Sumando dos enteros con signos diferentes”, restar la magnitud menor de la magnitud mayor, por lo tanto 117−115 = 2. Debido a que −117 tiene la magnitud mayor y su signo es negativo, predecimos un signo negativo a la diferencia de las magnitudes. Así, −117 + 115 = −2.

Ejercicio

Utilice un diagrama de líneas numéricos para mostrar la suma 5 + (−11).

Contestar: −6

Propiedades de la adición de números enteros

Te complacerá saber que las propiedades de suma para números enteros también se aplican a la suma de enteros.

La propiedad conmutativa de la adición

Que a y b representen dos números enteros. Entonces,

\[a + b = b + a.\nonumber \]

Ejemplo 6

Mostrar que 5 + (−7) = −7 + 5.

Solución

El esquema de la línea numérico

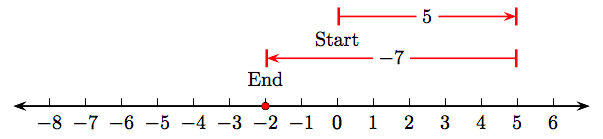
$Screen Shot 2019-08-14 a las 9.46.36 AM.png$

muestra que 5 + (−7) = −2. Por otro lado, el esquema de la recta numérica

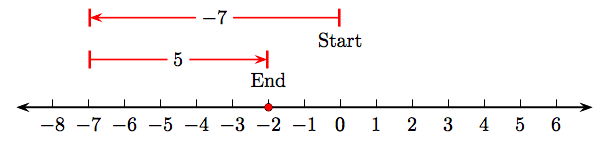
alt $Screen Shot 2019-08-14 a las 9.46.44 AM.png$

muestra que −7+5= −2. Por lo tanto, 5 + (−7) = −7 + 5.

Ejercicio

Utilice un diagrama de líneas numéricas para mostrar que −8 + 6 es lo mismo que 6 + (−8).

La suma de enteros también es asociativa.

La propiedad asociativa de la adición

Que a, b y c representen números enteros. Entonces,

\[(a + b) + c = a + (b + c)\nonumber \].

Ejemplo 7

Mostrar que (−9 + 6) + 2 = −9 + (6 + 2).

Solución

A la izquierda, los símbolos de agrupación exigen que sumemos −9 y 6 primero. Así,

\[ \begin{aligned} (−9 + 6) + 2 & = −3+2 \\ ~ & = −1. \end{aligned}\nonumber \]

A la derecha, los símbolos de agrupación exigen que primero sumemos 6 y 2. Así,

\[ \begin{aligned} −9 + (6 + 2) & = −9+8 \\ ~ & = −1. \end{aligned}\nonumber \]

Ambos lados simplifican a −1. Por lo tanto, (−9 + 6) + 2 = −9 + (6 + 2).

Ejercicio

Mostrar que la expresión (−8 + 5) + 3 es la misma que −8 + (5 + 3) simplificando cada una de las dos expresiones de forma independiente.

La propiedad de identidad aditiva

El número entero cero se llama la identidad aditiva. Si a es cualquier número entero, entonces

a +0= a y 0 + a = a.

Así, por ejemplo, −8+0= −8 y 0 + (−113) = −113.

Finalmente, cada entero tiene un opuesto único, llamado su inverso aditivo.

La propiedad inversa aditiva

Dejar a representar cualquier entero. Luego hay un entero único − a, llamado el inverso opuesto o aditivo de a, tal que

a + (− a) = 0 y − a + a = 0.

Ejemplo 8

Mostrar que 5 + (−5) = 0.

Solución

El esquema de la línea numérico

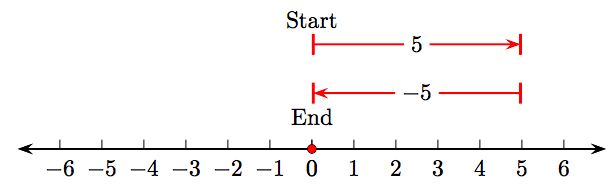
$Screen Shot 2019-08-14 a las 9.59.15 AM.png$

muestra claramente que 5 + (−5) = 0.

Ejercicio

Utilice un diagrama de líneas numéricas para mostrar que 9 + (−9) = 0.

Observación Importante

Hemos utilizado varias frases equivalentes para pronunciar el entero − a. Hemos utilizado “lo contrario de a”,” negativo a” y “el inverso aditivo de a”. Todas son pronunciaciones equivalentes.

Agrupación para la Eficiencia

El orden de las operaciones requiere que realicemos todas las adiciones a medida que ocurren, trabajando de izquierda a derecha.

Ejemplo 9

Simplifica −7+8+ (−9) + 12.

Solución

Realizamos las adiciones a medida que ocurren, trabajando de izquierda a derecha.

\[ \begin{aligned} =7 + 8 + (-9) +12 = 1 + (-9) +12 ~ & \textcolor{red}{ \text{ Working left to right, } -7 + 8 = 1.} \\ = -8 + 12 ~ & \textcolor{red}{ \text{ Working left to right, } 1 + (-9_ = -8.} \\ =4 ~ & \textcolor{red}{ ~ -8 + 12 = 4} \end{aligned}\nonumber \]

Así, −7+8+ (−9) + 12 = 4.

Ejercicio

Simplifica: −8+9+ (−4) + 2.

Contestar: −1

La propiedad conmutativa de la adición nos dice que cambiar el orden de adición no cambia la respuesta. La propiedad asociativa de suma nos dice que una suma no se ve afectada por el reagrupamiento. Trabajemos nuevamente el Ejemplo 9, primero agrupando números positivos y negativos juntos.

Ejemplo 10

Simplifica −7+8+ (−9) + 12.

Solución

Las propiedades conmutativas y asociativas nos permiten cambiar el orden de adición y reagrupación.

\[ \begin{aligned} -7 + 8 + (-9) + 12 = -7 + (-9) + 8 + 12 ~ & \textcolor{red}{ \text{ Use the commutative property to change the order.}} \\ = [-7+(-9)] + [8+12] ~ & \textcolor{red}{ \text{ Use the associative property to regroup.}} \\ =-16 + 20 ~ & \textcolor{red}{ \text{ Add the negatives. Add the positives.}} \\ =4 ~ & \textcolor{red}{ \text{ One final addition.}} \end{aligned}\nonumber \]

Así, −7+8+ (−9) + 12 = 4.

Ejercicio

Simplificar: −11 + 7 + (−12) + 3.

Contestar: −13

A primera vista, parece que no hay ninguna ventaja en utilizar la técnica del Ejemplo 10 sobre la técnica utilizada en el Ejemplo 9. No obstante, la técnica del Ejemplo 10 es mucho más rápida en la práctica, particularmente si se eliminan algunos de los pasos explicativos.

Agrupación eficiente

Cuando se le pide encontrar la suma de un número de enteros, es más eficiente agregar primero todos los enteros positivos, luego agregar los negativos, luego agregar los resultados.

Ejemplo 11

Simplifica −7+8+ (−9) + 12.

Solución

Agregue primero los enteros positivos, luego los negativos, luego agregue los resultados.

\[ \begin{aligned} -7 + 8 + (-9) +12 = 20 + (-16) ~ & \textcolor{red}{ \text{ Add the positives: } 8 + 12 = 20.} \\ ~ & \textcolor{red}{ \text{ Add the negatives: } -7 + (-9) = -16.} \\ =4 ~ & \textcolor{red}{ \text{ Add the results: } 20 + (-16) = 4.} \end{aligned}\nonumber \]

Así, −7+8+ (−9) + 12 = 4.

Ejercicio

Simplificar: −11 + 3 + (−2) + 7.

Contestar: −7

Uso de la notación correcta

¡Nunca escribas +−! Es decir, la notación

9 +−4 y − 8 +−6

no deben ser utilizados. En su lugar, use símbolos de agrupación de la siguiente manera:

9+ (−4) y −8+ (−6)

Ejercicios

En los Ejercicios 1-12, ¿qué entero está representado por el vector dado?

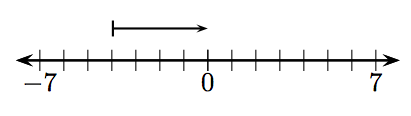
$Screen Shot 2019-08-14 a las 10.20.26 AM.png$

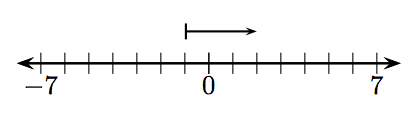
$Screen Shot 2019-08-14 a las 10.20.59 AM.png$

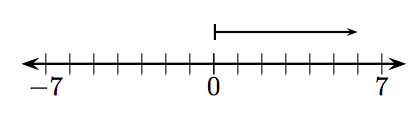
$Screen Shot 2019-08-14 a las 10.21.28 AM.png$

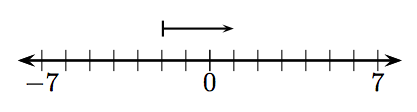
$Screen Shot 2019-08-14 a las 10.21.56 AM.png$

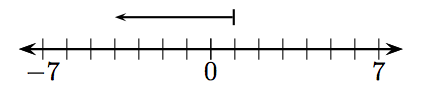
$Screen Shot 2019-08-14 a las 10.22.22 AM.png$

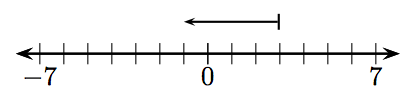
$Screen Shot 2019-08-14 a las 10.22.47 AM.png$

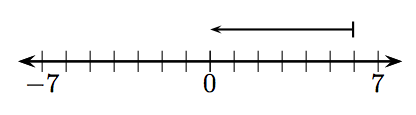
$Screen Shot 2019-08-14 a las 10.23.12 AM.png$

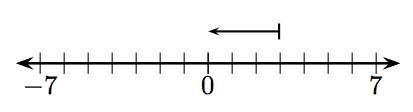
$Screen Shot 2019-08-14 a las 10.23.34 AM.png$

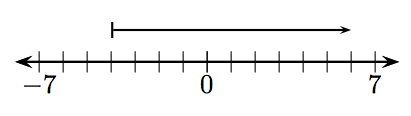
$Screen Shot 2019-08-14 a las 10.24.03 AM.png$

10.

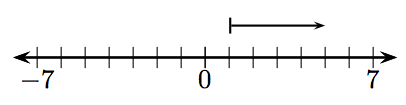
$Screen Shot 2019-08-14 a las 10.24.35 AM.png$

11.

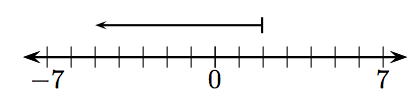
$Screen Shot 2019-08-14 a las 10.24.59 AM.png$

12.

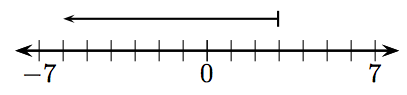
$Screen Shot 2019-08-14 a las 10.25.19 AM.png$

En los Ejercicios 13-36, encuentra la suma de los enteros dados.

13. −15 + 1

14. −1 + 18

15. 18 + (−10)

16. 2+ (−19)

17. −10 + (−12)

18. −1+ (−7)

19. 5 + 10

20. 1 + 12

21. 2+5

22. 14 + 1

23. 19 + (−15)

24. 20 + (−17)

25. −2+ (−7)

26. −14 + (−6)

27. −6 + 16

28. −2 + 14

29. −11 + (−6)

30. −7+ (−8)

31. 14 + (−9)

32. 5+ (−15)

33. 10 + 11

34. 14 + 11

35. −13 + 1

36. −8+2

En los Ejercicios 37-52, declarar la propiedad de adición representada por la identidad dada.

37. −1 + (3 + (−8)) = (−1 + 3) + (−8)

38. −4 + (6 + (−5)) = (−4 + 6) + (−5)

39. 7+ (−7) = 0

40. 14 + (−14) = 0

41. 15 + (−18) = −18 + 15

42. 14 + (−8) = −8 + 14

43. −15 + 0 = −15

44. −11 + 0 = −11

45. −7 + (1 + (−6)) = (−7 + 1) + (−6)

46. −4 + (8 + (−1)) = (−4 + 8) + (−1)

47. 17 + (−2) = −2 + 17

48. 5+ (−13) = −13 + 5

49. −4+0= −4

50. −7+0= −7

51. 19 + (−19) = 0

52. 5+ (−5) = 0

En los Ejercicios 53-64, indica la inversa aditiva del entero dado.

53. 18

54. 10

55. 12

56. 15

57. −16

58. −4

59. 11

60. 13

61. −15

62. −19

63. −18

64. −9

En Ejercicios 65-80, encuentra la suma de los enteros dados.

65. 6+ (−1) + 3 + (−4)

66. 6+ (−3) + 2 + (−7)

67. 15 + (−1) + 2

68. 11 + (−16) + 16

69. −17 + 12 + 3

70. −5+ (−3) + 2

71. 7 + 20 + 19

72. 14 + (−14) + (−20)

73. 4+ (−8) + 2 + (−5)

74. 6+ (−3) + 7 + (−2)

75. 7+ (−8) + 2 + (−1)

76. 8+ (−9) + 5 + (−3)

77. 9+ (−3) + 4 + (−1)

78. 1+ (−9) + 7 + (−6)

79. 9 + 10 + 2

80. −6 + 15 + (−18)

81. Cuenta Bancaria. Gerry abrió una nueva cuenta bancaria, depositando un cheque por 215 dólares. Luego realizó varios retiros de $40, 75 y $20 antes de depositar otro cheque por $185. ¿Cuánto hay ahora en la cuenta de Gerry?

82. Hundimiento del Mar Muerto. Debido al movimiento de las placas tectónicas, el Mar Muerto se hunde aproximadamente 1 metro cada año. Si actualmente es −418 metros ahora, ¿cuál será la elevación del Mar Muerto en 5 años? Escribir una expresión que modele esta situación y calme el resultado.

83. Ganancias y Pérdidas. Las ganancias y pérdidas correspondientes a los primeros seis meses del ejercicio fiscal para una pequeña empresa se muestran en el siguiente gráfico de barras. Suma las ganancias y pérdidas de cada mes. ¿Hubo una ganancia o pérdida neta durante el sexenio? ¿Cuánto?

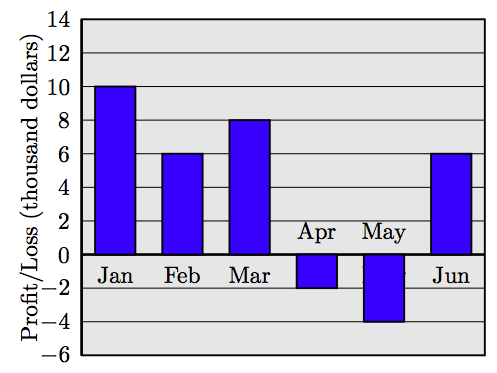
$Screen Shot 2019-08-14 at 10.31.07 AM.png$

84. Ganancias y Pérdidas. Las ganancias y pérdidas correspondientes a los primeros seis meses del ejercicio fiscal para una pequeña empresa se muestran en el siguiente gráfico de barras. Suma las ganancias y pérdidas de cada mes. ¿Hubo una ganancia o pérdida neta durante el sexenio? ¿Cuánto?

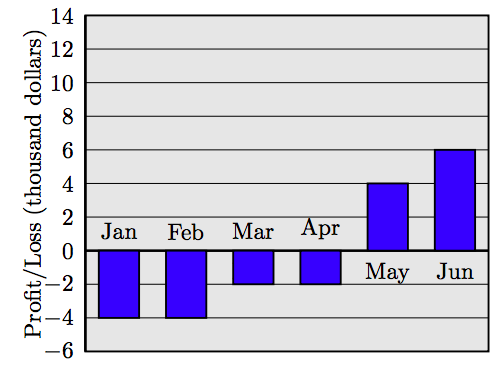
$Screen Shot 2019-08-14 at 10.31.14 AM.png$

RESPUESTAS

1. 4

3. 6

5. −5

7. −6

9. 10

11. −7

13. −14

15. 8

17. −22

19. 15

21. 7

23. 4

25. −9

27. 10

29. −17

31. 5

33. 21

35. −12

37. Propiedad asociativa de adición

39. Propiedad inversa aditiva

41. Propiedad conmutativa de adición

43. Propiedad de identidad aditiva

45. Propiedad asociativa de adición

47. Propiedad conmutativa de adición

49. Propiedad de identidad aditiva

51. Propiedad inversa aditiva

53. −18

55. −12

57. 16

59. −11

61. 15

63. 18

65. 4

67. 16

69. −2

71. 46

73. −7

75. 0

77. 9

79. 21

81. $265

83. Beneficio Neto: $24,000

Search

Text Color

Text Size

Margin Size

Font Type