2.6: Resolver ecuaciones
- Page ID
- 113440
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Recordemos (ver Sección 1.6) que una variable es un símbolo (generalmente una letra) que representa un valor que varía. Si una variable en una ecuación es reemplazada por un número y resulta una declaración verdadera, entonces ese número se llama una solución de la ecuación.
Ejemplo 1
¿Es −6 una solución de la ecuación 2x +5= −7?
Solución
Sustituye −6 por x en la ecuación.
\[ \begin{aligned} 2x + 5 = 7 ~ & \textcolor{red}{ \text{ Original equation.}} \\ 2(-6)+5 = -7 ~ & \textcolor{red}{ \text{ Substitute } -6 \text{ for } x.} \\ -12 + 5 = -7 ~ & \textcolor{red}{ \text{ On the left, multiply first.}} \\ -7 = -7 ~ & \textcolor{red}{ \text{ On the left, add.}} \end{aligned}\nonumber \]
Debido a que la última declaración es una declaración verdadera, −6 es una solución de la ecuación.
Ejercicio
¿−4 es una solución de 8 − 2 x = 5?
- Contestar
-
No
Sumando o restando la misma cantidad
Dos ecuaciones que tienen el mismo conjunto de soluciones son equivalentes. Por ejemplo, 2 x +5 = −7 y x = −6 tienen las mismas soluciones. Por lo tanto, son ecuaciones equivalentes. Ciertas operaciones algebraicas producen ecuaciones equivalentes.
Producción de ecuaciones equivalentes
Agregar la misma cantidad a ambos lados de una ecuación. Si empezamos con la ecuación
\[a = b,\nonumber \]
luego agregar c a ambos lados de la ecuación produce la ecuación equivalente
\[ a + c = b + c.\nonumber \]
Restar la Misma Cantidad de Ambos Lados de una Ecuación. Si empezamos con la ecuación
\[a = b,\nonumber \]
luego restar c de ambos lados de la ecuación produce la ecuación equivalente
\[a − c = b − c.\nonumber \]
Es decir, sumar o restar la misma cantidad de ambos lados de una ecuación no cambiará las soluciones de la ecuación.
Ejemplo 2
Resuelve para x: x + 3= −7.
Solución
Para deshacer el efecto de sumar 3, resta 3 de ambos lados de la ecuación.
\[ \begin{aligned} x + 3 = -7 ~ & \textcolor{red}{ \text{ Original equation.}} \\ x + 3 - 3 = -7 -3 ~ & \textcolor{red}{ \text{ Subtract 3 from both sides.}} \\ x = -7 + (-3) ~ & \begin{array}{l} \textcolor{red}{ \text{ Simplify the left hand side. On the right,}} \\ \textcolor{red}{ \text{ express subtractions as adding the opposite.}} \end{array} \\ x = -10 \end{aligned}\nonumber \]
Para verificar la solución, sustituya −10 por x en la ecuación original y simplifique.
\[ \begin{aligned} x + 3 = -7 ~ & \textcolor{red}{ \text{ Original equation.}} \\ -10 + 3 = -7 ~ & \textcolor{red}{ \text{ Substitute } -10 \text{ for } x.} \\ =7 = -7 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
Dado que la última línea de la comprobación es una declaración verdadera, esto confirma que −10 es una solución.
Ejercicio
Resuelve para x: x + 9 = -11.
- Contestar
-
x = −20
Ejemplo 3
Resolver para x: x − 8 = −11.
Solución
Para deshacer el efecto de restar 8, suma 8 a ambos lados de la ecuación.
\[ \begin{aligned} x - 8 = -11 ~ & \textcolor{red}{ \text{ Original equation.}} \\ x - 8 + 8 = -11+ 8 ~ & \textcolor{red}{ \text{ Add 8 to both sides.}} \\ x = -3 ~ & \textcolor{red}{ \text{ Simplify both equations.}} \end{aligned}\nonumber \]
Para verificar la solución, sustituya −3 por x en la ecuación original y simplifique.
\[ \begin{aligned} x - 8 = -11 ~ & \textcolor{red}{ \text{ Original equation.}} \\ -3 - 8 = -11 ~ & \textcolor{red}{ \text{ Substitute } -3 \text{ for } x.} \\ -11 = -11 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
Dado que la última línea de la comprobación es una declaración verdadera, esto confirma que −3 es una solución.
Ejercicio
Resolver para x: x − 2 = −7
- Contestar
-
x = −5
A veces hay un poco de simplificación en orden antes de iniciar el proceso de solución.
Ejemplo 4
Resolver para y: −8+2= y − 11 (−4).
Solución
Primero, simplificar ambos lados de la ecuación.
\[ \begin{aligned} -8 + 2 = y -11(-4) ~ & \textcolor{red}{ \text{ Original equation.}} \\ -6 = y -(-44) ~ & \begin{array}{l} \textcolor{red}{ \text{ Simplify. On the left, } -8 + 2 = -6.} \\ \textcolor{red}{ \text{ On the right, } 11(-4) = -44.} \end{array} \\ -6 = y + 44 - 44 ~ & \textcolor{red}{ \text{ Subtract 44 from both sides of the equation.}} \\ -6 + (-44) = y ~ & \textcolor{red}{ \text{ Express subtraction as addition. Simplify on the right.}} \\ -50 = y \end{aligned}\nonumber \]
Para verificar la solución, sustituya −50 por y en la ecuación original y simplifique.
\[ \begin{aligned} -8 + 2 = y -11(-4) ~ & \textcolor{red}{ \text{ Original equation.}} \\ -8 + 2 = -50 -11 (-4) ~ & \textcolor{red}{ \text{ Substitute } -50 \text{ for } y.} \\ -6 = -50 -(-44) ~ & \textcolor{red}{ \text{ Express subtraction on the right as addition.}} \\ -6 = -6 ~ & \textcolor{red}{ \text{ On the right, add: } -50 + 44 = -6.} \end{aligned}\nonumber \]
Dado que la última línea de la comprobación es una declaración verdadera, esto confirma que −50 es una solución.
Ejercicio
Resolver para y: y + 2 (−4) = −8+6
- Contestar
-
y = 6
Multiplicar o dividir por la misma cantidad
Sumar y restar no es la única manera de producir una ecuación equivalente.
Producción de ecuaciones equivalentes
Multiplicar ambos lados de una ecuación por la misma cantidad. Si empezamos con la ecuación
\[a = b,\nonumber \]
luego multiplicar ambos lados de la ecuación por c produce la ecuación equivalente
\[ a \cdot c = b \cdot c, \text{ or equivalently, } ac = bc,\nonumber \]
siempre c ≠ 0.
Dividiendo ambos lados de una ecuación por la misma cantidad. Si empezamos con la ecuación
\[ a = b,\nonumber \]
luego dividir ambos lados de la ecuación por c produce la ecuación equivalente
\[ \frac{a}{c} = \frac{b}{c},\nonumber \]
siempre c ≠ 0.
Es decir, multiplicar o dividir ambos lados de una ecuación por la misma cantidad no cambiará las soluciones de la ecuación.
Ejemplo 5
Resolver para x: −3 x = 30.
Solución
Para deshacer el efecto de multiplicar por −3, divida ambos lados de la ecuación por −3.
\[ \begin{aligned} -3x = 30 ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{-3x}{-3} = \frac{30}{-3} ~ & \textcolor{red}{ \text{ Divide both sides by }-3.} \\ x = -10 ~ & \begin{array}{l} \textcolor{red}{ \text{ On the left, } -3 \text{ times } x, \text{ divided by } -3 \text{ is } x.} \\ \textcolor{red}{ \text{ On the right, } 30/(-3)=-10.} \end{array} \end{aligned}\nonumber \]
Para verificar la solución, sustituya −10 por x en la ecuación original y simplifique.
\[ \begin{aligned} -3x = 30 ~ & \textcolor{red}{ \text{ Original equation.}} \\ -3(-10) = 30 ~ & \textcolor{red}{ \text{ Substitute } -10 \text{ for } x.} \\ 30 - 30 ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Debido a que la última línea de la comprobación es una declaración verdadera, esto confirma que −10 es una solución.
Ejercicio
Resolver para z: −4z = −28
- Contestar
-
z = 7
Ejemplo 6
Resolver para x:\( \frac{x}{-2} = -20\).
Solución
Para deshacer el efecto de dividir por −2, multiplique ambos lados de la ecuación por −2.
\[ \begin{aligned} \frac{x}{-2} = -20 ~ & \textcolor{red}{ \text{ Original equation.}} \\ -2 \left( \frac{x}{-2} \right) - -2 (-20) ~ & \textcolor{red}{ \text{ Multiply both sides by } -2.} \\ x = 40 ~ & \begin{array}{l} \textcolor{red}{ \text{ On the left, } x \text{ divided by } -2, \text{ multiplied by } -2,} \\ \textcolor{red}{ \text{ the result is } x. \text{ On the right, } -2(-20) = 40.} \end{array} \end{aligned}\nonumber \]
Para verificar la solución, sustituya 40 por x en la ecuación original y simplifique.
\[ \begin{aligned} \frac{x}{-2} = -20 ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{40}{-2} = -20 ~ & \textcolor{red}{ \text{ Substitute 40 for } x.} \\ -20 = -20 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
Debido a que la última línea del cheque es una afirmación verdadera, esto confirma que 40 es una solución.
Combinando Operaciones
Recordemos la discusión “Envolver” y “Desenvolver” de la Sección 1.6. Para envolver un regalo nosotros: (1) colocamos el papel de regalo, (2) colocamos la cinta adhesiva y (3) colocamos el lazo decorativo. Para desenvolver el regalo, debemos “deshacer” cada uno de estos pasos en orden inverso. De ahí que para desenvolver el regalo: (1) quitamos el lazo decorativo, (2) quitamos la cinta y (3) quitamos el papel de regalo.
Ahora, imagina una máquina que toma su entrada, entonces: (1) multiplica la entrada por 2, y (2) agrega 3 al resultado. Esta máquina se muestra a la izquierda en la Figura 2.16.
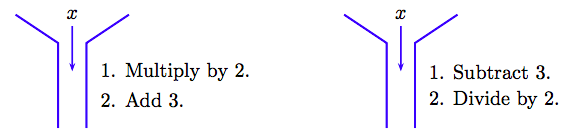
Para “desenvolver” el efecto de la máquina a la izquierda, necesitamos una máquina que “deshaga” cada uno de los pasos de la primera máquina, pero en orden inverso. La máquina de “desenvolver” se muestra a la derecha en la Figura 2.16. Primero restará tres de su entrada, luego dividirá el resultado por 2. Obsérvese que cada una de estas operaciones “deshace” la operación correspondiente de la primera máquina, pero en orden inverso.
Por ejemplo, coloque el entero 7 en la primera máquina a la izquierda en la Figura 2.16. Primero, doblamos 7, luego agregamos 3 al resultado. El resultado es 2 (7) + 3 = 17.
Ahora, para “desenvolver” este resultado, caemos 17 en la segunda máquina. Primero restamos 3, luego dividimos por 2. El resultado es (17 − 3) /2 = 7, la entrada entera original en la primera máquina.
Ahora, considere la ecuación
\[2x +3=7.\nonumber \]
A la izquierda, el orden de las operaciones exige que primero multipliquemos x por 2, luego sumemos 3. Para resolver esta ecuación para x, debemos “deshacer” cada una de estas operaciones en orden inverso. Así, (1) restaremos tres de ambos lados de la ecuación, luego (2) dividiremos ambos lados de la ecuación resultante por 2.
\[ \begin{aligned} 2x + 3 - 3 = 7 - 3 ~ & \textcolor{red}{ \text{ Subtract 3 from both sides.}} \\ 2x = 4 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ \frac{2x}{2} = \frac{4}{2} ~ & \textcolor{red}{ \text{ Divide both sides by 2.}} \\ x = 2 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
Los lectores deben verificar esta solución en la ecuación original.
Ejemplo 7
Resolver para x:\(\frac{x}{4} - 3 = -7\).
Solución
A la izquierda, el orden de operaciones exige que primero dividamos x por 4, luego restemos 3. Para resolver esta ecuación para x, debemos “deshacer” cada una de estas operaciones en orden inverso. Así, (1) agregaremos 3 a ambos lados de la ecuación, luego (2) multiplicaremos ambos lados de la ecuación resultante por 4.
\[ \begin{aligned} \frac{x}{4} - 3 = -7 ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{x}{4} - 3 + 3 = -7 + 3 ~ & \textcolor{red}{ \text{ Add 3 to both sides.}} \\ \frac{x}{4} = -4 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ 4 \left( \frac{x}{4} \right) = 4 (-4) ~ & \textcolor{red}{ \text{ Multiply both sides by 4.}} \\ x = -16 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
Cheque
Sustituye −16 por x en la ecuación original.
\[ \begin{aligned} \frac{x}{4} - 3 = 7 ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{-16}{4} - 3 = -7 ~ & \textcolor{red}{ \text{ Substitute } -16 \text{ for } x.} \\ -4 -3 = -7 ~ & \textcolor{red}{ \text{ Divide first: } -16/4 = -4.} \\ -7 = - 7 ~ & \textcolor{red}{ \text{ Subtract: } -4 -3 = -7.} \end{aligned}\nonumber \]
Debido a que la última línea de la comprobación es una declaración verdadera, −16 es una solución de la ecuación original.
Ejercicio
Resolver para x:
\[ \frac{x}{2} + 6 = 4\nonumber \]
- Contestar
-
x = -4
Ejemplo 8
Resolver para t: 0=8 − 2 t.
Solución
A la derecha, el orden de las operaciones exige que primero multipliquemos t por −2, luego sumemos 8. Para resolver esta ecuación para t, debemos “deshacer” cada una de estas operaciones en orden inverso. Así, (1) restaremos 8 de ambos lados de la ecuación, luego (2) dividiremos ambos lados de la ecuación resultante por −2.
\[ \begin{aligned} 0 = 8 -2t ~ & \textcolor{red}{ \text{ Original equation.}} \\ 0 - 8 = 8 - 2t - 8 ~ & \textcolor{red}{ \text{ Subtract 8 from both sides.}} \\ -8 = -2t ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ \frac{-8}{-2} = \frac{-2t}{-2} ~ & \textcolor{red}{ \text{ Divide both sides by 2.}} \\ 4 = t ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
Cheque
Sustituye 4 por t en la ecuación original.
\[ \begin{aligned} 0 = 8 - 2t ~ & \textcolor{red}{ \text{ Original equation.}} \\ 0 = 8 - 2(4) ~ & \textcolor{red}{ \text{ Substitute 4 for } t.} \\ 0 = 8-8 ~ & \textcolor{red}{ \text{ Multiply first: 2(4) = 8.}} \\ 0 = 0 ~ & \textcolor{red}{ \text{ Subtract: } 8-8=0.} \end{aligned}\nonumber \]
Debido a que la última línea del cheque es una declaración verdadera, 4 es una solución de la ecuación original.
Ejercicio
Resolver para r: 0 = 9 + 3 r
- Contestar
-
r = -3
Ejemplo 9
Resolver para p:\(-12 + 3 = -8+4 + \frac{p}{-3}.\)
Solución
Siempre simplifique cuando sea posible.
\[ \begin{aligned} -12+3= -8+4+ \frac{p}{-3} ~ & \textcolor{red}{ \text{ Origianl equation.}} \\ -9 = -4 + \frac{p}{-3} ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
A la derecha, el orden de las operaciones exige que primero dividamos p por −3, luego sumemos −4. Para resolver esta ecuación para p, debemos “deshacer” cada una de estas operaciones en orden inverso. Así, (1) agregaremos un 4 positivo a ambos lados de la ecuación, luego (2) multiplicaremos ambos lados de la ecuación resultante por −3.
\[ \begin{aligned} -9+-4 = -4+ \frac{p}{-3} + 4~ & \textcolor{red}{ \text{ Add 4 to both sides.}} \\ -5 = \frac{p}{-3} ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ -3(-5) = -3 \left( \frac{p}{-3} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by } -3.} \\ 15 = p ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
Cheque
Sustituye 15 por p en la ecuación original.
\[ \begin{aligned} -12 + 3 = =8 + 4 + \frac{p}{-3} ~ & \textcolor{red}{ \text{ Original equation.}} \\ -12 + 3 = -8 + 4 + \frac{15}{-3} ~ & \textcolor{red}{ \text{ Substitute 15 for } p.} \\ -9 = -8 + 4 + (-5) ~ & \begin{aligned} \textcolor{red}{ \text{ On the left, add: } -12 + 3 = -9. \text{ On the }} \\ \textcolor{red}{ \text{ right, divide: } 15/(-3) = -5.} \end{aligned} \\ -9 = -4 + (-5) ~ & \textcolor{red}{ \text{ On the right, } -8 + 4 = -4.} \\ -9 = -9 ~ & \textcolor{red}{ \text{ On the right, add: } -4 + (-5) = -9.} \end{aligned}\nonumber \]
Debido a que la última línea del cheque es una afirmación verdadera, 15 es una solución de la ecuación original.
Ejercicio
Resolver para q:
\[ \frac{q}{-2} -9 = -8+3\nonumber \]
- Contestar
-
q = −8
Aplicaciones
Veamos algunas aplicaciones de ecuaciones que involucran números enteros. Primero, recordamos a los lectores que una solución de un problema de palabras debe incorporar cada uno de los siguientes pasos.
Requisitos para soluciones de problemas de Word
- Configura un Diccionario de Variables. Debes dejar saber a tus lectores qué representa cada variable en tu problema. Esto se puede lograr de varias maneras:
- Declaraciones como “Que P represente el perímetro del rectángulo”.
- Etiquetar valores desconocidos con variables en una tabla.
- Etiquetar cantidades desconocidas en un boceto o diagrama.
- Configura una Ecuación. Toda solución a un problema de palabras debe incluir una ecuación cuidadosamente elaborada que describa con precisión las restricciones en la declaración del problema.
- Resuelve la Ecuación. Siempre debes resolver la ecuación establecida en el paso anterior.
- Responda a la Pregunta. Este paso se pasa por alto fácilmente. Por ejemplo, el problema podría preguntar por la edad de Jane, pero la solución de tu ecuación da la edad de la hermana de Jane, Liz. Asegúrate de responder la pregunta original hecha en el problema. Su solución debe escribirse en una oración con las unidades correspondientes.
- Mira hacia atrás. Es importante señalar que este paso no implica que simplemente deba verificar su solución en su ecuación. Después de todo, es posible que tu ecuación modele incorrectamente la situación del problema, por lo que podrías tener una solución válida a una ecuación incorrecta. La pregunta importante es: “¿Tiene sentido tu respuesta con base en las palabras de la declaración original del problema”.
Ejemplo 10
La cuenta bancaria de un estudiante está sobregirada. Después de hacer una su cuenta, Allen descubre que está sobregirado por 15 dólares. ¿Cuál era el saldo de su cuenta antes de su retiro? depósito de 120 dólares, encuentra que su cuenta sigue sobregirada por un monto de 75 dólares. ¿Cuál era su saldo antes de hacer su depósito?
Solución
En nuestra solución, abordamos cada paso de los Requisitos para Soluciones de Problemas de Word.
1. Configura un Diccionario de Variables. En este caso, lo desconocido es el saldo original en la cuenta del alumno. Que B represente este saldo original.
2. Configura una Ecuación. Un entero positivo representa un saldo saludable, mientras que un número negativo representa una cuenta que está sobregirada. Después del depósito del alumno, la cuenta sigue siendo sobregirada por 75 dólares. Diremos que este saldo es de −$75. Por lo tanto,
\[ \begin{array}{c c c c c} \colorbox{cyan}{Original Balance} & \text{plus} & \colorbox{cyan}{Student Deposit} & \text{equals} & \colorbox{cyan}{Current Balance} \\ B & + & $120 & = & -$75 \end{array}\nonumber \]
3. Resuelve la Ecuación. Para “deshacer” la suma, resta 120 de ambos lados de la ecuación.
\[ \begin{aligned} B + 120 = -75 ~ & \textcolor{red}{ \text{ Original equation.}} \\ B + 120 - 120 = -75 - 120 ~ & \textcolor{red}{ \text{ Subtract 120 from both sides.}} \\ B = -195 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
4. Responda a la Pregunta. El saldo original fue sobregirado por la suma de 195 dólares.
5. Mira hacia atrás. Si el saldo original fue sobregirado por 195 dólares, entonces dejamos que −$195 represente este saldo. El alumno realiza un depósito de $120. Agregue esto al saldo original para obtener −$195 + $120 = −$75, el saldo actual correcto.
Ejercicio
Después de retirar 125 dólares de su cuenta, Allen descubre que está sobregirado por 15 dólares. ¿Cuál era el saldo de su cuenta antes de su retiro?
- Contestar
-
$110
Ejemplo 11
Tres más del doble de un cierto número es −11. Encuentra el número desconocido.
Solución
En nuestra solución, abordamos cada paso de los Requisitos para Soluciones de Problemas de Word.
1. Configura un Diccionario de Variables. Que x represente el número desconocido. 2. Configura una Ecuación. “Tres más del doble de un número determinado” se convierte en:
\[ \begin{array}{c c c c c} \colorbox{cyan}{Three} & \text{more than} & \colorbox{cyan}{Twice a Certain Number} & \text{is} & \colorbox{cyan}{-11} \\ 3 & + & 2x & = & 11 \end{array}\nonumber \]
3. Resuelve la Ecuación. A la izquierda, el orden de las operaciones requiere que primero multipliquemos x por 2, luego sumemos 3. Para resolver esta ecuación para x, debemos “deshacer” cada una de estas operaciones en orden inverso. Así, (1) restaremos 3 de ambos lados de la ecuación, luego (2) dividiremos ambos lados de la ecuación resultante por 2.
\[ \begin{aligned} 3 + 2x = -11 ~ & \textcolor{red}{ \text{ Original equation.}} \\ 3 + 2x - 3 = -11 - 3 ~ & \textcolor{red}{ \text{ Subtract 3 from both sides.}} \\ 2x = -14 ~ & \textcolor{red}{ \text{ Simplify both sides.}} ~ \\ \frac{2x}{2} = \frac{-14}{2} ~ & \textcolor{red}{ \text{ Divide both sides by 2.}} \\ x = -7 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
4. Responda a la Pregunta. El número desconocido es −7.
5. Mira hacia atrás. ¿La respuesta satisface las limitaciones del problema? Tres más de dos veces −7 es tres más de −14, o −11. Entonces la solución es correcta.
Ejercicio\(\PageIndex{1}\)
Cinco menos del doble de un cierto número es −7. Encuentra el número desconocido.
- Contestar
-
−1
Ejercicios
1. ¿−11 es una solución de 2x +3= −19?
2. ¿−8 es una solución de 2x +7= −9?
3. ¿6 es una solución de 3x + 1 = 19?
4. ¿−6 es una solución de 2x +7= −5?
5. ¿12 es una solución de 4x +5= −8?
6. ¿Es −8 una solución de −3x + 8 = 18?
7. ¿15 es una solución de 2x +6= −9?
8. ¿3 es una solución de −4x +1= −20?
9. ¿−15 es una solución de −3x +6= −17?
10. ¿Es −18 una solución de −3x +9= −9?
11. ¿Es −6 una solución de −2x + 3 = 15?
12. ¿7 es una solución de −3x +5= −16?
En los Ejercicios 13-28, resuelve la ecuación dada para x.
13. x − 13 = 11
14. x − 6 = 12
15. x − 3=6
16. x − 3 = −19
17. x + 10 = 17
18. x +3=9
19. x − 6=1
20. x − 10 = 12
21. x − 15 = −12
22. x − 2 = 13
23. x + 11 = −19
24. x + 3 = 17
25. x +2=1
26. x +2= −20
27. x +5= −5
28. x + 14 = −15
En los Ejercicios 29-44, resuelve la ecuación dada para x.
29. −x = −20
30. 5x = −35
31. \(\frac{x}{−7}\)= 10
32. \(\frac{x}{−6}\)= −20
33. \(\frac{x}{−10}\)= 12
34. \(\frac{x}{2}\)= 11
35. \(\frac{x}{9}\)= −16
36. \(\frac{x}{−3}\)= −7
37. −10x = 20
38. −17x = −85
39. 14x = 84
40. −10x = −40
41. −2x = 28
42. −14x = 42
43. \(\frac{x}{−10}\)= 15
44. \(\frac{x}{−8}\)= −1
En Ejercicios 45-68, resuelve la ecuación dada para x.
45. −4x − 4 = 16
46. −6x − 14 = 4
47. 4x − 4 = 76
48. −5x − 15 = 45
49. 5x − 14 = −79
50. 15x − 2 = 43
51. −10x − 16 = 24
52. 2x − 7 = −11
53. 9x +5= −85
54. 8x +8= −16
55. 7x + 15 = −55
56. 2x +2= −38
57. −x + 8 = 13
58. −5x + 20 = −50
59. 12x − 15 = −3
60. −19x − 17 = −36
61. 4x − 12 = −56
62. 7x − 16 = 40
63. 19x + 18 = 113
64. −6x + 20 = −64
65. −14x + 12 = −2
66. −9x + 5 = 104
67. 14x + 16 = 44
68. −14x + 10 = −60
69. Dos menos de ocho veces un número desconocido es −74. Encuentra el número desconocido.
70. Seis menos de tres veces un número desconocido es 21. Encuentra el número desconocido.
71. Ocho más de dos veces un número desconocido es 0. Encuentra el número desconocido.
72. Cinco más de ocho veces un número desconocido es −35. Encuentra el número desconocido.
73. El número −6 es 2 más que un número desconocido. Encuentra el número desconocido.
74. El número −4 es 7 más que un número desconocido. Encuentra el número desconocido.
75. Tres más de ocho veces un número desconocido es −29. Encuentra el número desconocido.
76. Cuatro más de nueve veces un número desconocido es 85. Encuentra el número desconocido.
77. Los puntajes de Alan en sus tres primeros exámenes son 79, 61 y 54. ¿Qué debe puntuar Alan en su próximo examen para promediar 71 para los cuatro exámenes?
78. Los puntajes de Benny en sus tres primeros exámenes son 54, 68 y 54. ¿Qué debe anotar Benny en su próximo examen para promediar 61 para los cuatro exámenes?
79. El cociente de dos enteros es 5. Uno de los números enteros es −2. Encuentra el otro entero.
80. El cociente de dos enteros es 3. Uno de los números enteros es −7. Encuentra el otro entero.
81. El cociente de dos enteros es 9. Uno de los números enteros es −8. Encuentra el otro entero.
82. El cociente de dos enteros es 9. Uno de los números enteros es −2. Encuentra el otro entero.
83. El número −5 es 8 más que un número desconocido. Encuentra el número desconocido.
84. El número −6 es 8 más que un número desconocido. Encuentra el número desconocido.
85. La cuenta bancaria de un estudiante está sobregirada. Después de hacer un depósito de 260 dólares, encuentra que su cuenta aún está sobregirada por un monto de 70 dólares. ¿Cuál era su saldo antes de hacer su depósito?
86. La cuenta bancaria de un estudiante está sobregirada. Después de hacer un depósito de 300 dólares, encuentra que su cuenta aún está sobregirada por un monto de 70 dólares. ¿Cuál era su saldo antes de hacer su depósito?
87. La cuenta bancaria de un estudiante está sobregirada. Después de hacer un depósito de 360 dólares, encuentra que su cuenta aún está sobregirada por un monto de 90 dólares. ¿Cuál era su saldo antes de hacer su depósito?
88. La cuenta bancaria de un estudiante está sobregirada. Después de hacer un depósito de 260 dólares, encuentra que su cuenta aún está sobregirada por un monto de 50 dólares. ¿Cuál era su saldo antes de hacer su depósito?
89. El número −10 es −5 veces mayor que un número desconocido. Encuentra el número desconocido.
90. El número −3 es −3 veces mayor que un número desconocido. Encuentra el número desconocido. 91. El número −15 es −5 veces mayor que un número desconocido. Encuentra el número desconocido.
92. El número −16 es 4 veces mayor que un número desconocido. Encuentra el número desconocido.
93. Dos menos de nueve veces un número desconocido es 7. Encuentra el número desconocido.
94. Cuatro menos de dos veces un número desconocido es 8. Encuentra el número desconocido.
95. Los puntajes de Mark en sus tres primeros exámenes son 79, 84 y 71. ¿Qué puntaje debe marcar en su próximo examen para promediar 74 para los cuatro exámenes?
96. Los puntajes de Alan en sus tres primeros exámenes son 85, 90 y 61. ¿Qué debe puntuar Alan en su próximo examen para promediar 77 para los cuatro exámenes?
RESPUESTAS
1. Sí
3. Sí
5. No
7. No
9. No
11. Sí
13. 24
15. 9
17. 7
19. 7
21. 3
23. −30
25. −1
27. −10
29. 20
31. −70
33. −120
35. −144
37. −2
39. 6
41. −14
43. −150
45. −5
47. 20
49. −13
51. −4
53. −10
55. −10
57. −5
59. 1
61. −11
63. 5
65. 1
67. 2
69. −9
71. −4
73. −8
75. −4
77. 90
79. −10
81. −72
83. −13
85. −330 $
87. −$450
89. 2
91. 3
93. 1
95. 62


