4.2: Fracciones Equivalentes
- Page ID
- 113462
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En esta sección tratamos fracciones, números o expresiones de la forma a/b.
Definición: Fracciones
Un número de la forma
\[ \dfrac{a}{b}\nonumber \]
donde\(a\) y\(b\) son números se llama fracción. Al número\(a\) se le llama numerador de la fracción, mientras que al número\(b\) se le llama denominador de la fracción.
Cerca del final de esta sección, veremos que el numerador y denominador de una fracción también pueden ser expresiones algebraicas, pero por el momento restringimos nuestra atención a fracciones cuyos numeradores y denominadores son enteros. Comenzamos nuestro estudio de fracciones con la definición de fracciones equivalentes.
Fracciones Equivalentes
Dos fracciones son equivalentes si representan el mismo valor numérico.
Pero, ¿cómo podemos saber si dos fracciones representan el mismo número? Bueno, una técnica implica algunas visualizaciones simples. Considere la imagen mostrada en la Figura 4.1, donde la región sombreada representa 1/3 del área total de la figura (una de las tres regiones iguales está sombreada).

En la Figura 4.2, hemos sombreado 2/6 de toda la región (dos de seis regiones iguales están sombreadas).

En la Figura 4.3, hemos sombreado 4/12 de toda la región (cuatro de doce regiones iguales están sombreadas).
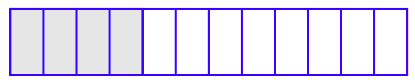
Tomemos los diagramas de la Figura 4.1, la Figura 4.2 y la Figura 4.3 y los apilemos uno encima del otro, como se muestra en la Figura 4.4.
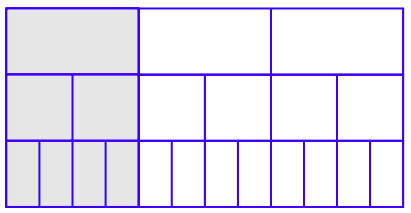
La Figura 4.4 proporciona evidencia visual sólida de que las siguientes fracciones son equivalentes.
\[ \dfrac{1}{3} = \dfrac{2}{6} = \dfrac{4}{12}\nonumber \]
Observaciones clave
1. Si empezamos con la fracción 1/3, luego multiplicamos tanto el numerador como el denominador por 2, obtenemos el siguiente resultado.
\[ \begin{aligned} \dfrac{1}{3} = \dfrac{1 \cdot 2}{3 \cdot 2} ~ & \textcolor{red}{ \text{ Multiply the numerator and denominator by 2.}} \\ = \dfrac{2}{6} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
Esto es precisamente lo mismo que sucede pasando de la Figura 4.1 a 4.2, donde duplicamos el número de cajas disponibles (pasando de 3 disponibles a 6 disponibles) y duplicamos el número de cajas sombreadas (pasando de 1 sombreada a 2 sombreada).
2. Si empezamos con la fracción 1/3, luego multiplicamos tanto el numerador como el denominador por 4, obtenemos el siguiente resultado.
\[ \begin{aligned} = \dfrac{1}{3} = \dfrac{1 \cdot 4}{3 \cdot 4} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 4.}} \\ = \dfrac{4}{12} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
Esto es precisamente lo mismo que sucede pasando de la Figura 4.1 a 4.3, donde multiplicamos el número de cajas disponibles por 4 (pasando de 3 disponibles a 12 disponibles) y multiplicamos el número de cajas sombreadas por 4 (pasando de 1 sombreada a 4 sombreada).
La discusión anterior motiva el siguiente resultado fundamental.
Creación de fracciones equivalentes
Si comienzas con una fracción, entonces multiplica tanto su numerador como su denominador por el mismo número, la fracción resultante es equivalente (tiene el mismo valor numérico) a la fracción original. En símbolos,
\[ \dfrac{a}{b} = \dfrac{a \cdot x}{b \cdot x}\nonumber \]
Argumentar a la inversa
Revertir el argumento anterior también es cierto.
1. Si empezamos con la fracción 2/6, luego dividimos tanto el numerador como el denominador por 2, obtenemos el siguiente resultado.
\[ \begin{aligned} \dfrac{2}{6} = \dfrac{2 \div 2}{6 \div 2} ~ & \textcolor{red}{ \text{ Divide numerator and denominator by 2.}} \\ = \dfrac{1}{3} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
Esto es precisamente lo mismo que sucede yendo hacia atrás de la Figura 4.2 a 4.1, donde dividimos el número de cajas disponibles por 2 (pasando de 6 disponibles a 3 disponibles) y dividiendo el número de cajas sombreadas por 2 (pasando de 2 sombreadas a 1 sombreadas).
2. Si empezamos con la fracción 4/12, luego dividimos tanto el numerador como el denominador por 4, obtenemos el siguiente resultado.
\[ \begin{aligned} \dfrac{4}{12} = \dfrac{4 \div 4}{12 \div 4} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 4.}} \\ = \dfrac{1}{3} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
Esto es precisamente lo mismo que sucede yendo hacia atrás de la Figura 4.3 a 4.1, donde dividimos el número de cajas disponibles por 4 (pasando de 12 disponibles a 3 disponibles) y dividimos la alineación numérica de cajas sombreadas por 4 (pasando de 4 sombreadas a 1 sombreadas).
La discusión anterior motiva el siguiente resultado fundamental.
Creación de fracciones equivalentes
Si comienzas con una fracción, entonces divide tanto su numerador como su denominador por el mismo número, la fracción resultante es equivalente (tiene el mismo valor numérico) a la fracción original. En símbolos,
\[ \dfrac{a}{b} = \dfrac{a \div x}{b \div x}.\nonumber \]
El mayor divisor común
Necesitamos un poco más de terminología.
Divisor
Si d y a son números naturales, decimos que “d divide a” si y sólo si cuando a se divide por d, el resto es cero. En este caso, decimos que “d es un divisor de a”.
Por ejemplo, cuando 36 se divide por 4, el resto es cero. En este caso, decimos que “4 es un divisor de 36”. Por otro lado, cuando 25 se divide por 4, el resto no es cero. En este caso, decimos que “4 no es un divisor de 25”.
Divisor común más grande
Que a y b sean números naturales. Los divisores comunes de a y b son aquellos números naturales que dividen tanto a como b. El divisor más común es el más grande de estos divisores comunes.
Ejemplo 1
Encuentra el mayor divisor común de 18 y 24.
Solución
Primero enumere los divisores de cada número, los números que dividen cada número con cero resto.
Divisores de 18:1, 2, 3, 6, 9 y 18
Divisores de 24:1, 2, 3, 4, 6, 8, 12 y 24
Los divisores comunes son:
Divisores comunes: 1, 2, 3 y 6
El divisor más común es el más grande de los divisores comunes. Es decir,
Divisor común más grande = 6.
Es decir, el mayor número que divide tanto 18 como 24 es el número 6.
Ejercicio
Encuentra el mayor divisor común de 12 y 18.
- Contestar
-
6
Reducción de una Fracción a los Términos más bajos
Primero, una definición.
Términos más bajos
Se dice que una fracción se reduce a términos más bajos si el divisor más común tanto del numerador como del denominador es 1.
Así, por ejemplo, 2/3 se reduce a términos más bajos debido a que la mayor división común de 2 y 3 es 1. Por otro lado, 4/6 no se reduce a términos más bajos debido a que el mayor divisor común de 4 y 6 es 2.
Ejemplo 2
Reducir la fracción 18/24 a los términos más bajos.
Solución
Una técnica que funciona bien es dividir tanto el numerador como el denominador por el mayor divisor común del numerador y denominador. En el Ejemplo 1, vimos que el mayor divisor común de 18 y 24 es 6. Dividimos tanto el numerador como el denominador entre 6 para obtener
\[ \begin{aligned} \dfrac{18}{24} = \dfrac{18 \div 6}{24 \div 6} ~ & \textcolor{red}{ \text{ Divide numerator and denominator by 6.}} \\ = \dfrac{3}{4} ~ & \textcolor{red}{ \text{ Simplify numerator and dice.}} \end{aligned}\nonumber \]
Tenga en cuenta que el mayor divisor común de 3 y 4 es ahora 1. Así, 3/4 se reduce a los términos más bajos.
Hay una segunda manera de mostrar división del numerador y denominador por 6. Primero, factoriza tanto el numerador como el denominador de la siguiente manera:
\[ \begin{aligned} \dfrac{18}{24} = \dfrac{3 \cdot 6}{4 \cdot 6} ~ & \textcolor{red}{ \text{ Factor out a 6.}} \end{aligned}\nonumber \]
Entonces puedes mostrar “división” tanto del numerador como del denominador por 6 “tachando” o “cancelando” un 6 en el numerador para un 6 en el denominador, así:
\[ \begin{aligned} = \dfrac{3 \cdot \cancel{6}}{4 \cdot \cancel{6}} ~ & \textcolor{red}{ \text{ Cancel common factor.}} \\ = \dfrac{3}{4} \end{aligned}\nonumber \]
Tenga en cuenta que obtenemos la misma fracción equivalente, reducida a términos más bajos, es decir 3/4.
Ejercicio
Reducir la fracción 12/18 a los términos más bajos.
- Contestar
-
2/3
Punto Importante
En el Ejemplo 2 vimos que 6 era tanto un divisor como un factor de 18. Las palabras divisor y factor son equivalentes.
Utilizamos la siguiente técnica en nuestra segunda solución en el Ejemplo 2.
Regla de Cancelación
Si expresas numerador y denominador como producto, entonces puedes cancelar factores comunes del numerador y denominador. El resultado será una fracción equivalente.
Debido a la “regla de cancelación”, una de las formas más efectivas de reducir una fracción a términos más bajos es primero encontrar factorizaciones primos tanto para el numerador como para el denominador, luego cancelar todos los factores comunes.
Ejemplo 3
Reducir la fracción 18/24 a los términos más bajos.
Solución
Utilice árboles de factores para cebar el numerador de factores y el denominador.
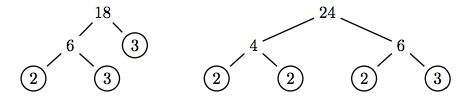
Una vez que hemos factorizado el numerador y el denominador, cancelamos los factores comunes.
\[ \begin{aligned} \dfrac{18}{24} = \dfrac{2 \cdot 3 \cdot 3}{2 \cdot 2 \cdot 2 \cdot 3} ~ & \textcolor{red}{ \text{ Prime factor numerator and denominator.}} \\ = \dfrac{ \cancel{2} \cdot \cancel{3} \cdot 3}{ \cancel{2} \cdot 2 \cdot 2 \cdot \cancel{3}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \dfrac{3}{2 \cdot 2} ~ & \textcolor{red}{ \text{ Remaining factors.}} \\ = \dfrac{3}{4} ~ & \textcolor{red}{ \text{ Simplify denominator.}} \end{aligned}\nonumber \]
Así, 18/24 = 3/4.
Ejercicio\(\PageIndex{1}\)
Reducir la fracción 28/35 a los términos más bajos.
- Contestar
-
4/5
Ejemplo 4
Reducir la fracción 28/42 a los términos más bajos.
Solución
Utilice árboles de factores para cebar el numerador de factores y el denominador.
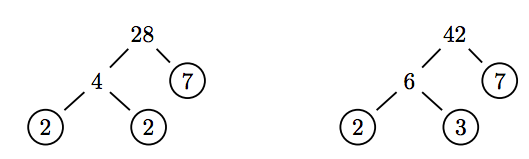
Ahora podemos cancelar factores comunes.
\[ \begin{aligned} \dfrac{28}{42} = \dfrac{2 \cdot 2 \cdot 7}{2 \cdot 3 \cdot 7} ~ & \textcolor{red}{ \text{ Prime factor numerator and denominator.}} \\ = \dfrac{ \cancel{2} \cdot 2 \cdot \cancel{7}}{ \cancel{2} \cdot 3 \cdot \cancel{7}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \dfrac{2}{3} \end{aligned}\nonumber \]
Así, 28/42 = 2/3.
Ejercicio
Reducir la fracción 36/60 a los términos más bajos.
- Contestar
-
3/5
Reducción de Fracciones con Variables
Utilizamos exactamente la misma técnica para reducir fracciones cuyos numeradores y denominadores contienen variables.
Ejemplo 5
Reducir
\[ \dfrac{56x^2y}{60xy^2}\nonumber \]
a los términos más bajos.
Solución
Utilice árboles de factores para factorizar los coeficientes de numerador y denominador.

Ahora cancela factores comunes.
\[ \begin{aligned} \dfrac{56x^2y}{60xy^2} = \dfrac{2 \cdot 2 \cdot 2 \cdot 7 \cdot x \cdot x \cdot y}{2 \cdot 2 \cdot 3 \cdot 5 \cdot x \cdot y \cdot y} ~ & \textcolor{red}{ \text{ Prime factor numerator and denominator.}} \\ = \dfrac{ \cancel{2} \cdot \cancel{2} \cdot 2 \cdot 7 \cdot \cancel{x} \cdot x \cdot \cancel{y}}{ \cancel{2} \cdot \cancel{2} \cdot 3 \cdot 5 \cdot \cancel{x} \cdot y \cdot \cancel{y}} ~ & \textcolor{red}{ \text{ Cancel cmmon factors.}} \\ = \dfrac{2 \cdot 7 \cdot x}{3 \cdot 5 \cdot y} ~ & \textcolor{red}{ \text{ Remaining factors.}} \\ = \dfrac{14x}{15y} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
Así, 56x 2 y/ (60xy 2) = 14x/ (15y).
Ejercicio
Reducir:
\[ \dfrac{25a^3b}{40a^2b^3}\nonumber \]
- Contestar
-
\[ \dfrac{5a}{8b^2}\nonumber \]
Una palabra sobre notación matemática
Hay dos tipos de notación matemática: (1) notación matemática en línea y (2) notación matemática mostrada.
Notación matemática en línea
La notación 14 x/(15 y) se denomina notación matemática inline. Cuando la misma expresión se centra en su propia línea, como en
\[ \dfrac{14x}{15y},\nonumber \]
este tipo de notación se llama notación matemática visualizada.
Cuando se trabaja un problema a mano, usando cálculos a lápiz y papel, el formato preferido es la notación mostrada, como la notación mostrada utilizada para simplificar la expresión dada en el Ejemplo 5. Sin embargo, las computadoras y calculadoras requieren que ingrese sus expresiones usando notación matemática en línea. Por lo tanto, es extremadamente importante que seas igualmente competente ya sea con notación matemática: visualizada o inline.
Por cierto, el orden de las operaciones, cuando se aplica a la expresión inline 14x/ (15y), requiere que primero realicemos la multiplicación dentro de los paréntesis. Entonces debemos realizar multiplicaciones y divisiones a medida que ocurren, a medida que avanzamos de izquierda a derecha a través de la expresión. Es por eso que la notación en línea 14x/ (15y) es equivalente a la notación mostrada
\[ \dfrac{14x}{15y}.\nonumber \]
No obstante, la expresión 14x/15y es una bestia diferente. No hay paréntesis, por lo que realizamos multiplicación y división a medida que ocurren, moviéndonos de izquierda a derecha a través de la expresión. Así, primero debemos tomar el producto de 14 y x, dividir el resultado por 15, luego multiplicar por y. En la notación mostrada, este resultado es equivalente a
\[ \dfrac{14x}{15} \cdot y,\nonumber \]
que es un resultado diferente.
Algunos lectores podrían preguntarse por qué no usamos la notación (14x)/(15y) para describir la solución en el Ejemplo 5. Después de todo, esta notación en línea también es equivalente a la notación mostrada
\[ \dfrac{14x}{15y}.\nonumber \]
No obstante, el punto es que no necesitamos hacerlo, ya que orden de operaciones ya requiere que tomemos el producto de 14 y x antes de dividirlo por 15y. Si esto le está lastimando la cabeza, sepa que es bastante aceptable usar la notación equivalente (14x)/(15y) en lugar de 14x/ (15y). Ambos son correctos.
Fracciones Equivalentes en Términos Superiores
En ocasiones surge la necesidad de encontrar una fracción equivalente con un denominador diferente, mayor.
Ejemplo 6
Expresar 3/5 como fracción equivalente que tiene denominador 20.
Solución
La clave aquí es recordar que multiplicar numerador y denominador por un mismo número produce una fracción equivalente. Para obtener una fracción equivalente con un denominador de 20, tendremos que multiplicar el numerador y denominador de 3/5 por 4.
\[ \begin{aligned} \dfrac{3}{5} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 4.}} \\ = \dfrac{12}{20} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
Por lo tanto, 3/5 equivale a 12/20.
Ejercicio
Expresar 2/3 como fracción equivalente que tiene denominador 21.
- Contestar
-
14/21
Ejemplo 7
Expresar 8 como fracción equivalente que tiene denominador 5.
Solución
La clave aquí es señalar que
\[ \begin{aligned} 8 = \dfrac{8}{1} ~ & \textcolor{red}{ \text{ Understood denominator is 1.}} \end{aligned}\nonumber \]
Para obtener una fracción equivalente con un denominador de 5, tendremos que multiplicar el numerador y denominador de 8/1 por 5.
\[ \begin{aligned} = \dfrac{8 \cdot 5}{1 \cdot 5} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 5.}} \\ = \dfrac{40}{5} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
Por lo tanto, 8 equivale a 40/5.
Ejercicio
Expresar 5 como fracción equivalente que tiene denominador 7.
- Contestar
-
35/7
Ejemplo 8
Expresar 2/9 como fracción equivalente que tiene denominador 18 a.
Solución
Para obtener una fracción equivalente con un denominador de 18 a, tendremos que multiplicar el numerador y denominador de 2/9 por 2 a.
\[ \begin{aligned} \dfrac{2}{9} = \dfrac{2 \cdot 2a}{9 \cdot 2a} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by } 2a.} \\ = \dfrac{4a}{18a} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
Por lo tanto, 2/9 equivale a 4 a/(18 a), o equivalentemente, (4 a)/(18 a).
Ejercicio
Expresar 3/8 como fracción equivalente que tiene denominador 24 a.
- Contestar
-
\[ \dfrac{9a}{24a}\nonumber \]
Fracciones Negativas
También tenemos que lidiar con fracciones que son negativas. Primero, hablemos de la colocación del signo negativo.
- Positivo dividido por negativo es negativo, entonces
\[ \dfrac{3}{-5} = - \dfrac{3}{5}.\nonumber \]
- Pero también es cierto que negativo dividido por positivo es negativo. Así,
\[ \dfrac{−3}{5} = \dfrac{−3}{5}.\nonumber \]
Estas dos observaciones implican que las tres fracciones siguientes son equivalentes (el mismo número):
\[ \dfrac{3}{-5} = - \dfrac{3}{5} = \dfrac{-3}{5}.\nonumber \]
Tenga en cuenta que hay tres posibles colocaciones para el signo negativo: (1) el denominador, (2) la barra de fracciones, o (3) el numerador. Cualquiera de estas colocaciones produce una fracción equivalente.
Fracciones y Signos Negativos
Sea a y b cualquier número entero. Las tres fracciones siguientes son equivalentes (mismo número):
\[ \dfrac{a}{-b} = - \dfrac{a}{b} = \dfrac{-a}{b}.\nonumber \]
Los matemáticos prefieren colocar el signo negativo ya sea en el numerador o en la barra de fracciones. Se desaconseja el uso de un signo negativo en el denominador.
Ejemplo 9
Reducir:
\[ \dfrac{50x^3}{-75x^5}\nonumber \]
a los términos más bajos.
Solución
Numerador de factor primo y denominador y cancelar.
\[ \begin{aligned} \dfrac{50x^3}{-75x^5} &= \dfrac{2 \cdot 5 \cdot 5 \cdot x \cdot x \cdot x}{-3 \cdot 5 \cdot 5 \cdot x \cdot x \cdot x \cdot x \cdot x} \\ &= \dfrac{2 \cdot \cancel{5} \cdot \cancel{5} \cdot \cancel{x} \cdot \cancel{x} \cdot \cancel{x}}{-3 \cdot \cancel{5} \cdot \cancel{5} \cdot \cancel{x} \cdot \cancel{x} \cdot \cancel{x} \cdot x \cdot x} \\ &= \dfrac{2}{-3 \cdot x \cdot x} \\ &= \dfrac{2}{-3x^2} \end{aligned}\nonumber \]
No obstante, se prefiere que no haya signos negativos en el denominador, así que coloquemos el signo negativo en la barra de fracciones (el numerador también le convendría). Así,
\[ \dfrac{50x^3}{-75x^5} = - \dfrac{2}{3x^2}\nonumber \]
También tenemos el siguiente resultado.
Fracciones y Signos Negativos
Dejar\(a\) y\(b\) ser cualquier número entero. Entonces,
\[ \dfrac{-a}{-b} = \dfrac{a}{b}.\nonumber \]
Ejemplo 10
Reducir:
\[ \dfrac{-12xy^2}{-18x^2y}\nonumber \]
Solución
A diferencia del Ejemplo 9, a algunos les gusta cuidar primero el signo de la respuesta.
\[ \dfrac{-12xy^2}{-18x^2y} = \dfrac{12xy^2}{18x^2y}\nonumber \]
Ahora podemos factorizar numerador y denominador y cancelar factores comunes.
\[ \begin{aligned} &= \dfrac{2 \cdot 2 \cdot 3 \cdot x \cdot y \cdot y}{2 \cdot 3 \cdot 3 \cdot x \cdot x \cdot y} \\ &= \dfrac{ \cancel{2} \cdot 2 \cancel{3} \cdot \cancel{x} \cdot y \cdot \cancel{y}}{ \cancel{2} \cdot \cancel{3} \cdot 3 \cdot \cancel{x} \cdot x \cdot \cancel{y}} &= \dfrac{2y}{3x} \end{aligned}\nonumber \]
Así,
\[ \dfrac{-12xy^2}{-18x^2y} = \dfrac{2y}{3x}.\nonumber \]
Ejercicio
Reducir:
\[ \dfrac{-21a^2b^3}{-56a^3b}\nonumber \]
- Contestar
-
\[ \dfrac{3b^2}{8a}\nonumber \]
Ejercicios
En Ejercicios 1-12, encuentra el GCD de los números dados.
1. 72, 8
2. 76, 52
3. 52, 20
4. 56, 96
5. 36, 63
6. 63, 21
7. 72, 44
8. 10, 40
9. 16, 56
10. 54, 66
11. 84, 24
12. 75, 45
En los Ejercicios 13-28, reducir la fracción dada a los términos más bajos.
13. \(\dfrac{22}{98}\)
14. \(\dfrac{28}{56}\)
15. \(\dfrac{93}{15}\)
16. \(\dfrac{90}{39}\)
17. \(\dfrac{69}{21}\)
18. \(\dfrac{74}{62}\)
19. \(\dfrac{74}{12}\)
20. \(\dfrac{66}{10}\)
21. \(\dfrac{66}{57}\)
22. \(\dfrac{34}{30}\)
23. \(\dfrac{33}{99}\)
24. \(\dfrac{20}{58}\)
25. \(\dfrac{69}{24}\)
26. \(\dfrac{18}{96}\)
27. \(\dfrac{46}{44}\)
28. \(\dfrac{92}{24}\)
29. Expresar 3 como fracción equivalente que tiene denominador 24. 30. Expresar 3 como fracción equivalente que tiene denominador 8. 31. Expresar\(\dfrac{25}{19}\) como fracción equivalente teniendo denominador 57. 32. Expresar\(\dfrac{29}{22}\) como fracción equivalente teniendo denominador 44. 33. Expresar 2 como fracción equivalente que tiene denominador 2. 34. Expresar 2 como fracción equivalente que tiene denominador 8. 35. Expresar\(\dfrac{18}{19}\) como fracción equivalente teniendo denominador 95. 36. Expresar\(\dfrac{17}{22}\) como fracción equivalente teniendo denominador 44. 37. Expresar\(\dfrac{1}{3}\) como fracción equivalente teniendo denominador 24. 38. Expresar\(\dfrac{15}{19}\) como fracción equivalente que tiene denominador 95. 39. Expresar 16 como fracción equivalente que tiene denominador 4. 40. Expresar 5 como fracción equivalente que tiene denominador 2.
En los Ejercicios 41-56, reducir la fracción dada a los términos más bajos.
41. \(\dfrac{34}{−86}\)
42. \(\dfrac{−48}{14}\)
43. \(\dfrac{−72}{−92}\)
44. \(\dfrac{27}{−75}\)
45. \(\dfrac{−92}{82}\)
46. \(\dfrac{−44}{−62}\)
47. \(\dfrac{−21}{33}\)
48. \(\dfrac{57}{−99}\)
49. \(\dfrac{22}{−98}\)
50. \(\dfrac{−33}{69}\)
51. \(\dfrac{42}{−88}\)
52. \(\dfrac{−100}{48}\)
53. \(\dfrac{94}{−6}\)
54. \(\dfrac{−36}{−38}\)
55. \(\dfrac{10}{−86}\)
56. \(\dfrac{−100}{−46}\)
57. Expresar\(\dfrac{3}{2}\) como fracción equivalente que tiene denominador 62n.
58. Expresar\(\dfrac{6}{25}\) como fracción equivalente que tiene denominador 50a.
59. Expresar\(\dfrac{13}{10}\) como fracción equivalente teniendo denominador 60m.
60. Expresar\(\dfrac{1}{16}\) como fracción equivalente que tiene denominador 80p.
61. Expresar\(\dfrac{3}{2}\) como fracción equivalente que tiene denominador 50n.
62. Expresar\(\dfrac{43}{38}\) como fracción equivalente que tiene denominador 76a.
63. Expresar 11 como fracción equivalente que tiene denominador 4m. 64. Express 13 como fracción equivalente que tiene denominador 6n.
65. Express 3 como fracción equivalente que tiene denominador 10m.
66. Expresar 10 como fracción equivalente que tiene denominador 8b.
67. Expresar 6 como fracción equivalente que tiene denominador 5n.
68. Expresar 16 como fracción equivalente que tiene denominador 2y.
En los Ejercicios 69-84, reducir la fracción dada a los términos más bajos.
69. \(\dfrac{82y^5}{−48y}\)
70. \(\dfrac{−40y^5}{−55y}\)
71. \(\dfrac{−77x^5}{44x^4}\)
72. \(\dfrac{−34x^6}{−80x}\)
73. \(\dfrac{−14y^5}{54y^2}\)
74. \(\dfrac{96y^4}{−40y^2}\)
75. \(\dfrac{42x}{81x^3}\)
76. \(\dfrac{26x^2}{32x^6}\)
77. \(\dfrac{−12x^5}{14x^6}\)
78. \(\dfrac{−28y^4}{72y^6}\)
79. \(\dfrac{−74x}{22x^2}\)
80. \(\dfrac{56x^2}{26x^3}\)
81. \(\dfrac{−12y^5}{98y^6}\)
82. \(\dfrac{96x^2}{14x^4}\)
83. \(\dfrac{18x^6}{−54x^2}\)
84. \(\dfrac{32x^6}{62x^2}\)
En los Ejercicios 85-100, reducir la fracción dada a los términos más bajos.
85. \(\dfrac{26y^2x^4}{−62y^6x^2}\)
86. \(\dfrac{6x^2y^3}{40x^3y^2}\)
87. \(\dfrac{−2y^6x^4}{−94y^2x^5}\)
88. \(\dfrac{90y^6x^3}{39y^3x^5}\)
89. \(\dfrac{30y^5x^5}{−26yx^4}\)
90. \( \dfrac{74x^6y^4}{−52xy^3}\)
91. \(\dfrac{36x^3y^2}{−98x^4y^5}\)
92. \(\dfrac{84x^3y}{16x^4y^2}\)
93. \(\dfrac{−8x^6y^3}{54x^3y^5}\)
94. \( \dfrac{70y^5x^2}{16y^4x^5}\)
95. \(\dfrac{34yx^6}{−58y^5x^4}\)
96. \(\dfrac{99y^2x^3}{88y^6x}\)
97. \(\dfrac{−36y^3x^5}{51y^2x}\)
98. \(\dfrac{44y^5x^5}{−88y^4x}\)
99. \(\dfrac{91y^3x^2}{−28y^5x^5}\)
100. \(\dfrac{−76y^2x}{−57y^5x^6}\)
101. Huracanes. Según la Administración Nacional Atmosférica y Oceánica, en 2008 hubo 16 tormentas nombradas, de las cuales 8 crecieron en huracanes y 5 fueron mayores.
i) ¿Qué fracción de tormentas nombradas se convirtió en huracanes? Reduzca su respuesta a los términos más bajos.
ii) ¿Qué fracción de tormentas nombradas fueron huracanes mayores? Reduzca su respuesta a los términos más bajos.
iii) ¿Qué fracción de huracanes fueron mayores? Reduzca su respuesta a los términos más bajos.
102. Tigres. Los tigres están en crítico declive debido a la invasión humana, la pérdida de más de nueve décimas partes de su hábitat y el creciente comercio de pieles de tigre y partes del cuerpo. Associated Press-Times-Standard 01/24/10 Monturas de presión para salvar al tigre.
i) Escribir la pérdida de hábitat como una fracción.
ii) Describir con palabras lo que representa el numerador y denominador de esta fracción.
iii) Si la fracción representa la pérdida de todo el hábitat original, ¿cuánto del hábitat original queda?
RESPUESTAS
1. 8
3. 4
5. 9
7. 4
9. 8
11. 12
13. \(\dfrac{11}{49}\)
15. \(\dfrac{31}{5}\)
17. \(\dfrac{23}{7}\)
19. \(\dfrac{37}{6}\)
21. \(\dfrac{22}{19}\)
23. \(\dfrac{1}{3}\)
25. \(\dfrac{23}{8}\)
27. \(\dfrac{23}{22}\)
29. \(\dfrac{72}{24}\)
31. \(\dfrac{75}{57}\)
33. \(\dfrac{4}{2}\)
35. \(\dfrac{90}{95}\)
37. \(\dfrac{8}{24}\)
39. \(\dfrac{64}{4}\)
41. \(\dfrac{−17}{43}\)
43. \(\dfrac{18}{23}\)
45. \(\dfrac{−46}{41}\)
47. \(\dfrac{− 7}{11}\)
49. \(\dfrac{−11}{49}\)
51. \(\dfrac{−21}{44}\)
53. \(\dfrac{−47}{3}\)
55. \(\dfrac{− 5}{43}\)
57. \(\dfrac{93 n}{62 n}\)
59. \(\dfrac{78 m}{60 m}\)
61. \(\dfrac{75 n}{50 n}\)
63. \(\dfrac{44 m}{4 m}\)
65. \(\dfrac{30 m}{10 m}\)
67. \(\dfrac{30 n}{5 n}\)
69. \(\dfrac{−41 y^4}{24}\)
71. \(\dfrac{− 7x}{4}\)
73. \(− \dfrac{7 y^3}{27}\)
75. \(\dfrac{14}{27 x^2}\)
77. \(− \dfrac{6}{7x}\)
79. \(− \dfrac{37}{11 x}\)
81. \(− \dfrac{6}{49 y}\)
83. \(− \dfrac{x^4}{3}\)
85. \(− \dfrac{13 x^2}{31 y^4}\)
87. \(\dfrac{y^4}{47 x}\)
89. \(− \dfrac{15 y^4 x}{13}\)
91. \(− \dfrac{18}{49xy^3}\)
93. \(− \dfrac{4 x^3}{27 y^2}\)
95. \(−\dfrac{17 x^2}{29 y^4}\)
97. \(− \dfrac{12yx^4}{17}\)
99. \(− \dfrac{13}{4y^2x^3}\)
101.
i)\(\dfrac{1}{2}\)
ii)\(\dfrac{5}{16}\)
iii)\(\dfrac{5}{8}\)


