4.5: Sumando y restando fracciones

Última actualización
Guardar como PDF

Page ID: 113461

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Paul y Tony ordenan una pizza que ha sido cortada en ocho rebanadas iguales. Así, cada rebanada es 1/8 de la pizza entera. Paul come dos rebanadas (sombreadas en gris claro en la Figura$\PageIndex{1}$), o 2/8 de toda la pizza. Tony come tres rebanadas (sombreadas en rojo claro (o un tono más oscuro de gris en impresión en blanco y negro) en la Figura$\PageIndex{1}$), o 3/8 de toda la pizza.

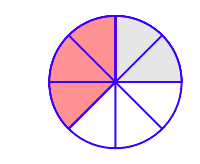
Screen Shot 2019-08-30 at 4.09.40 PM.png — Figura$\PageIndex{1}$: Paul se come dos rebanadas (2/8) y Tony se come tres rebanadas (3/8).

Debe quedar claro que juntos Paul y Tony comen cinco rebanadas, o 5/8 de toda la pizza. Esto refleja el hecho de que

\[ \frac{2}{8} + \frac{3}{8} = \frac{5}{8}.\nonumber \]

Esto demuestra cómo sumar dos fracciones con un denominador común (mismo). Conservar el denominador común y sumar los numeradores. Es decir,

\[ \begin{align*} \frac{2}{8} + \frac{3}{8} &= \frac{2 + 3}{8} ~ && \textcolor{red}{ \text{ Keep denominator; add numerators.}} \\ &= \frac{5}{8} ~ && \textcolor{red}{ \text{ Simplify numerator.}} \end{align*} \]

Sumando Fracciones con Denominadores Comunes

Dejar a/c y b/c sean dos fracciones con un denominador común (mismo). Su suma se define como

\[ \frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}\nonumber \]

Es decir, para sumar dos fracciones que tengan denominadores comunes, mantener el denominador común y sumar sus numeradores.

Una regla similar se mantiene para la resta.

Restar fracciones con denominadores comunes

Dejar a/c y b/c sean dos fracciones con un denominador común (mismo). Su diferencia se define como

\[ \frac{a}{c} - \frac{b}{c} = \frac{a-b}{c}.\nonumber \]

Es decir, restar dos fracciones que tienen denominadores comunes, mantener el denominador común y restar sus numeradores.

Ejemplo$\PageIndex{1}$

Encuentra la suma de 4/9 y 3/9.

Solución

Conservar el denominador común y sumar los numeradores.

\[ \begin{aligned} \frac{4}{9} + \frac{3}{9} &= \frac{4+3}{9} ~ & \textcolor{red}{ \text{ Keep denominator; add numerators.}} \\ &= \frac{7}{9} ~ & \textcolor{red}{ \text{ Simplify numerator.}} \end{aligned}\nonumber \]

Ejercicio$\PageIndex{1}$

Agregar:

\[ \frac{1}{8} + \frac{2}{8}\nonumber \]

Contestar: 3/8

Ejemplo$\PageIndex{2}$

Restar 5/16 de 13/16.

Solución

Mantener el denominador común y restar los numeradores.

\[ \begin{aligned} \frac{13}{16} - \frac{5}{16} &= \frac{13-5}{16} ~ & \textcolor{red}{ \text{ Keep denominator; subtract numerators.}} \\ &=\frac{8}{16} ~ & \textcolor{red}{ \text{ Simplify numerator.}} \end{aligned}\nonumber \]

Por supuesto, como aprendimos en la Sección 4.1, siempre debemos reducir nuestra respuesta final a los términos más bajos. Una forma de lograrlo en este caso es dividir el numerador y el denominador por 8, el mayor divisor común de 8 y 16.

\[ \begin{aligned} = \frac{8 \div 8}{16 \div 8} ~ & \textcolor{red}{ \text{ Divide numerator and denominator by 8.}} \\ = \frac{1}{2} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]

Ejercicio$\PageIndex{2}$

Restar:

\[ \frac{11}{12} - \frac{7}{12}\nonumber \]

Contestar: 1/3

Ejemplo$\PageIndex{3}$

Simplificar:

\[ \frac{3}{x} - \left( - \frac{7}{x} \right) .\nonumber \]

Solución

Ambas fracciones comparten un denominador común.

\[ \begin{aligned} \frac{3}{x} - \left( - \frac{7}{x} \right) &= \frac{3}{x} + \frac{7}{x} ~ & \textcolor{red}{ \text{ Add the opposite.}} \\ &= \frac{3+7}{x} ~ & \textcolor{red}{ \text{ Keep denominator, add numerators.}} \\ &= \frac{10}{x} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

Sumando fracciones con diferentes denominadores

Considera la suma

\[ \frac{4}{9} + \frac{1}{6}.\nonumber \]

No podemos sumar estas fracciones porque no tienen un denominador común. Entonces, ¿qué hacer?

Goles

Para sumar dos fracciones con diferentes denominadores, necesitamos:

Encuentra un denominador común para las fracciones dadas.
Hacer fracciones con el denominador común que sean equivalentes a las fracciones originales.

Si logramos los dos ítems en el “Objetivo”, podremos encontrar la suma de las fracciones dadas.

Entonces, ¿cómo empezar? Necesitamos encontrar un denominador común, pero no cualquier denominador común. Vamos a estar de acuerdo en que queremos mantener los números lo más pequeños posible y encontrar un mínimo denominador común.

Definición: Mínimo denominador común

El mínimo denominador común (LCD) para un conjunto de fracciones es el número más pequeño divisible por cada uno de los denominadores de las fracciones dadas.

Consideremos nuevamente la suma que deseamos encontrar:

\[ \frac{4}{9} + \frac{1}{6} .\nonumber \]

Los denominadores son 9 y 6. Deseamos encontrar un mínimo denominador común, el número más pequeño que sea divisible tanto por 9 como por 6. Se me vienen a la mente varios candidatos: 36, 54 y 72 son todos divisibles por 9 y 6, por mencionar algunos. Pero el número más pequeño que es divisible tanto por 9 como por 6 es 18. Este es el mínimo denominador común para 9 y 6.

Pasamos ahora al segundo ítem en “Gol”. Necesitamos hacer fracciones que tengan 18 como denominador que sean equivalentes a 4/9 y 1/6. En el caso de 4/9, si multiplicamos tanto el numerador como el denominador por 2, obtenemos

\[ \begin{aligned} \frac{4}{9} &= \frac{4 \cdot 2}{9 \cdot 2} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 2.}} \\ &= \frac{8}{18}. ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]

En el caso de 1/6, si multiplicamos tanto el numerador como el denominador por 3, obtenemos

\[ \begin{aligned} \frac{1}{6} &= \frac{1 \cdot 3}{6 \cdot 3} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 3.}} \\ &= \frac{3}{18}. ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]

Normalmente, organizaremos nuestro trabajo de la siguiente manera.

\[ \begin{aligned} \frac{4} + \frac{1}{6} &= \frac{4 \cdot \textcolor{red}{2}}{9 \cdot \textcolor{red}{2}} + \frac{1 \cdot \textcolor{red}{3}}{6 \cdot \textcolor{red}{3}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = 18.}} \\ &= \frac{8}{18} + \frac{3}{18} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ &= \frac{8+3}{18} ~ & \textcolor{red}{ \text{ Keep common denominator; add numerators.}} \\ &= \frac{11}{18} ~ & \textcolor{red}{ \text{ Simplify numerator.}} \end{aligned}\nonumber \]

Resumimos el procedimiento.

Sumando o restando fracciones con diferentes denominadores

Encuentra el LCD, el número más pequeño divisible por todos los denominadores de las fracciones dadas.
Crea fracciones usando la LCD como denominador que sean equivalentes a las fracciones originales.
Sumar o restar las fracciones equivalentes resultantes. Simplificar, incluida la reducción de la respuesta final a los términos más bajos.

Ejemplo$\PageIndex{4}$

Simplificar:$ \displaystyle \frac{3}{5} - \frac{2}{3}$.

Solución

El número más pequeño divisible por 5 y 3 es 15.

\[ \begin{aligned} \frac{3}{5} - \frac{2}{3} &= \frac{3 \cdot \textcolor{red}{3}}{5 \cdot \textcolor{red}{3}} - \frac{2 \cdot \textcolor{red}{5}}{3 \cdot \textcolor{red}{5}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = 15.}} \\ &= \frac{9}{15} - \frac{10}{15} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ &= \frac{9-10}{15} ~ & \textcolor{red}{ \text{ Keep LCD; subtract numerators.}} \\ &= \frac{-1}{15} ~ & \textcolor{red}{ \text{ Simplify numerator.}} \end{aligned}\nonumber \]

Si bien esta respuesta es perfectamente aceptable, negativa dividida por positiva nos da una respuesta negativa, por lo que también podríamos escribir

\[ = - \frac{1}{15}.\nonumber \]

Ejercicio$\PageIndex{4}$

Resta:

\[ \frac{3}{4} - \frac{7}{5}\nonumber \]

Contestar: -13/20

Ejemplo$\PageIndex{5}$

Simplificar:$-\frac{1}{4} - \frac{5}{6}$.

Solución

El número más pequeño divisible por 4 y 6 es 12.

\[ \begin{aligned} -\frac{1}{4} - \frac{5}{6} &= - \frac{1 \cdot \textcolor{red}{3}}{4 \cdot \textcolor{red}{3}} - \frac{5 \cdot \textcolor{red}{2}}{6 \cdot \textcolor{red}{2}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD =12.}} \\ &= - \frac{3}{12} - \frac{10}{12} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ &= \frac{-3-10}{12} ~ & \textcolor{red}{ \text{ Keep LCD; subtract numerators.}} \\ &= \frac{-13}{12} ~ & \textcolor{red}{ \text{ Simplify numerator.}} \end{aligned}\nonumber \]

Ejercicio$\PageIndex{5}$

Restar:$-\frac{3}{8} - \frac{1}{12}$

Contestar: -11/24

Ejemplo$\PageIndex{6}$

Simplificar:$\frac{5}{x} + \frac{3}{4}$.

Solución

El número más pequeño divisible tanto por 4 como por x es 4x.

\[ \begin{aligned} \frac{5}{x} + \frac{3}{4} = \frac{5 \cdot \textcolor{red}{4}}{x \cdot \textcolor{red}{4}} + \frac{3 \cdot \textcolor{red}{x}}{4 \cdot \textcolor{red}{x}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = }4x.} \\ = = \frac{20}{4x} + \frac{3x}{4x} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ = \frac{20 + 3x}{4x} ~ & \textcolor{red}{ \text{ Keep LCD; add numerators.}} \end{aligned}\nonumber \]

Ejercicio$\PageIndex{6}$

Agregar:

\[ \frac{5}{z} + \frac{2}{3}\nonumber \]

Contestar: \[ \frac{15+2z}{3z}\nonumber \]

Ejemplo$\PageIndex{7}$

Simplificar:$\frac{2}{3}- \frac{x}{5}$.

Solución

El número más pequeño divisible por 3 y 5 es 15.

\[ \begin{aligned} \frac{2}{3} - \frac{x}{5} = \frac{2 \cdot \textcolor{red}{5}}{3 \cdot \textcolor{red}{5}} - \frac{x \cdot \textcolor{red}{3}}{5 \cdot \textcolor{red}{3}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = 15.}} \\ = \frac{10}{15} - \frac{3x}{15} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ = \frac{10 - 3x}{15} ~ & \textcolor{red}{ \text{ Keep LCD; subtract numerators.}} \end{aligned}\nonumber \]

Múltiple menos común

Primero definimos el múltiplo de un número.

Definición: Multiples

Los múltiplos de un número d son 1 d, 2 d, 3 d, 4 d, etc. es decir, los múltiplos de d son los números nd, donde n es un número natural.

Por ejemplo, los múltiplos de 8 son 1 · 8, 2 · 8, 3 · 8, 4 · 8, etc., o equivalentemente, 8, 16, 24, 32, etc.

Definición: Mínimo Común Múltiple

El múltiplo menos común (LCM) de un conjunto de números es el número más pequeño que es un múltiplo de cada número del conjunto dado. El procedimiento para encontrar un MCM sigue:

Enumere todos los múltiplos de cada número en el conjunto de números dado.
Enumere los múltiplos que tienen en común.
Escoge el menor de los múltiplos que tienen en común.

Ejemplo$\PageIndex{7}$

Encuentra el múltiplo menos común (MCM) de 12 y 16.

Solución

Enumere los múltiplos de 12 y 16.

Multiplos de 12:12, 24, 36, 48, 60, 72, 84, 96,...

Multiplos de 16:16, 32, 48, 64, 80, 96, 112,...

Elige los múltiplos comunes.

Multiplos Comunes: 48, 96,...

El LCM es el menor de los múltiplos comunes.

MCM (12,16) = 48

Ejercicio$\PageIndex{7}$

Encuentra el mínimo denominador común de 6 y 9.

Contestar: 18

Observación Importante

El mínimo común denominador es el mínimo común múltiplo de los denominadores.

Por ejemplo, supongamos que su problema es 5/12 + 5/16. El LCD es el número más pequeño divisible tanto por 12 como por 16. Ese número es 48, que también es el LCM de 12 y 16. Por lo tanto, el procedimiento para encontrar el LCM también se puede utilizar para encontrar la pantalla LCD.

Múltiple menos común mediante factorización principal

También puedes encontrar el LCM usando factorización prima.

Factorización de LCM por Prime

Para encontrar un LCM para un conjunto de números, siga este procedimiento:

Anote la factorización prima para cada número en forma compacta usando exponentes.
El LCM se encuentra anotando cada factor que aparece en el paso 1 a la potencia más alta de ese factor que aparece.

Ejemplo$\PageIndex{8}$

Usa la factorización de primos para encontrar el mínimo común múltiplo encuentra el mínimo común denominador de 18 y 24. (LCM) de 12 y 16.

Solución

Factor primo 12 y 16.

\[ \begin{aligned} 12 = 2 \cdot 2 \cdot 3 \\ 16 = 2 \cdot 2 \cdot 2 \cdot 2 \end{aligned}\nonumber \]

Escribe las factorizaciones principales en forma compacta usando exponentes.

\[ \begin{aligned} 12 = 2^2 \cdot 3^1 \\ 16 = 2^4 \end{aligned}\nonumber \]

Para encontrar el LCM, anote cada factor que aparezca a la mayor potencia de ese factor que aparece. Los factores que aparecen son 2 y 3. El poder más alto de 2 que aparece es 2 ⁴. El poder más alto de 3 que aparece es 3 ¹.

\[ \begin{aligned} \text{LCM} = 2^4 \cdot 3^1 ~ & \textcolor{red}{ \text{ Keep highest power of each factor.}} \end{aligned}\nonumber \]

Ahora ampliamos esta última expresión para obtener nuestro LCM.

\[ \begin{aligned} = 16 \cdot 3 ~ & \textcolor{red}{ \text{ Expand: } 2^4 = 16 \text{ and } 3^1 = 3.} \\ = 48. ~ & \textcolor{red}{ \text{ Multiply.}} \end{aligned}\nonumber \]

Tenga en cuenta que esta respuesta es idéntica a la LCM que se encuentra en el Ejemplo 8 que se encontró al enumerar múltiplos y elegir el múltiplo más pequeño en común.

Ejercicio$\PageIndex{8}$

Usa la factorización prima para encontrar el mínimo denominador común de 18 y 24.

Contestar: 72

Ejemplo$\PageIndex{10}$

Simplificar:$\frac{5}{28} + \frac{11}{42}$.

Solución

Factorizar los denominadores en forma compacta usando exponentes.

28 = 2 · 2 · 7=2 ² · 7

42 = 2 · 3 · 7=2 ¹ · 3 ¹ · 7 ¹

Para encontrar la pantalla LCD, anote cada factor que aparezca a la mayor potencia de ese factor que aparece. Los factores que aparecen son 2, 3 y 7. El poder más alto de 2 que aparece es 2 ². El poder más alto de 3 que aparece es 3 ¹. El poder más alto de 7 que aparece es 7 ¹.

\[ \begin{aligned} \text{LCM} = 2^2 \cdot 3^1 \cdot 7^1 ~ & \textcolor{red}{ \text{ Keep highest power of each factor.}} \\ = 4 \cdot 3 \cdot 7 ~ & \textcolor{red}{ \text{ Expand: } 2^2 = 4, ~ 3^1 = 3, ~ 7^1 = 7.} \\ = 84 ~ & \textcolor{red}{ \text{ Multiply.}} \end{aligned}\nonumber \]

Crea fracciones equivalentes con la nueva pantalla LCD, luego agrega.

\[ \begin{aligned} \frac{5}{28} + \frac{11}{42} = \frac{5 \cdot \textcolor{red}{3}}{28 \cdot \textcolor{red}{3}} + \frac{11 \cdot \textcolor{red}{2}}{42 \cdot \textcolor{red}{2}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = 84.}} \\ = \frac{15}{84} + \frac{22}{84} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ = \frac{37}{84} ~ & \textcolor{red}{ \text{ Keep LCD; add numerators.}} \end{aligned}\nonumber \]

Ejercicio$\PageIndex{10}$

Simplificar:$ \frac{5}{24} + \frac{5}{36}$

Contestar: 25/72

Ejemplo$\PageIndex{11}$

Simplificar:$- \frac{11}{24} - \frac{1}{18}$.

Solución

Factorizar los denominadores en forma compacta usando exponentes.

24 = 2 · 2 · 2 · 3=2 ³ · 3 ¹

18 = 2 · 3 · 3=2 ¹ · 3 ²

Para encontrar la pantalla LCD, anote cada factor que aparezca a la mayor potencia de ese factor que aparece. Los factores que aparecen son 2 y 3. El poder más alto de 2 que aparece es 2 ³. El poder más alto de 3 que aparece es 3 ².

\[ \begin{aligned} \text{LCM} = 2^3 \cdot 3^2 ~ & \textcolor{red}{ \text{ Keep highest power of each factor.}} \\ = 8 \cdot 9 ~ & \textcolor{red}{ \text{ Expand: } 2^3 = 8 \text{ and } 3^2 = 9.} \\ = 72. ~ & \textcolor{red}{ \text{ Multiply.}} \end{aligned}\nonumber \]

Crea fracciones equivalentes con la nueva LCD, luego resta.

\[ \begin{aligned} - \frac{11}{24} - \frac{1}{18} = - \frac{11 \cdot \textcolor{red}{3}}{24 \cdot \textcolor{red}{3}} - \frac{1 \cdot \textcolor{red}{4}}{18 \cdot \textcolor{red}{4}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = 72.}} \\ = - \frac{33}{72} - \frac{4}{72} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ = \frac{-33-4}{72} ~ & \textcolor{red}{ \text{ Keep LCD; subtract numerators.}} \\ = \frac{-37}{72} ~ & \textcolor{red}{ \text{ Simplify numerator.}} \end{aligned}\nonumber \]

Por supuesto, negativo dividido por positivo arroja una respuesta negativa, por lo que también podemos escribir nuestra respuesta en la forma

\[ - \frac{11}{24} - \frac{1}{18} = - \frac{37}{72}.\nonumber \]

Ejercicio$\PageIndex{11}$

Simplificar:$ - \frac{5}{24} - \frac{11}{36}$

Contestar: −37/72

Comparando Fracciones

La forma más sencilla de comparar fracciones es crear fracciones equivalentes.

Ejemplo$\PageIndex{12}$

Organice las fracciones −1/2 y −4/5 en una recta numérica, luego compárelas usando el símbolo de desigualdad apropiado.

Solución

El mínimo denominador común para 2 y 5 es el número 10. Primero, hacer fracciones equivalentes con una LCD igual a 10.

\[ \begin{array}{c} - \frac{1}{2} = - \frac{1 \cdot \textcolor{red}{5}}{2 \cdot \textcolor{red}{5}} = - \frac{5}{10} \\ - \frac{4}{5} = - \frac{4 \cdot \textcolor{red}{2}}{5 \cdot \textcolor{red}{2}} = - \frac{8}{10} \end{array}\nonumber \]

Para trazar décimas, subdivida el intervalo entre −1 y 0 en diez incrementos iguales.

$Screen Shot 2019-08-30 a las 9.06.17 PM.png$

Porque −4/5 se encuentra a la izquierda de −1/2, tenemos que −4/5 es menor que −1/2, entonces escribimos

\[ - \frac{4}{5} < - \frac{1}{2}.\nonumber \]

Ejercicio$\PageIndex{12}$

Compara −3/8 y −1/2.

Contestar: \[ - \frac{1}{2} < - \frac{3}{8}\nonumber \]

Ejercicios

En los Ejercicios 1-10, enumere los múltiplos los números dados, luego enumere los múltiplos comunes. Seleccione el LCM de la lista de múltiplos comunes.

1. 9 y 15

2. 15 y 20

3. 20 y 8

4. 15 y 6

5. 16 y 20

6. 6 y 10

7. 20 y 12

8. 12 y 8

9. 10 y 6

10. 10 y 12

En los Ejercicios 11-20, para los números dados, calcular el LCM usando factorización prima.

11. 54 y 12

12. 108 y 24

13. 18 y 24

14. 36 y 54

15. 72 y 108

16. 108 y 72

17. 36 y 24

18. 18 y 12

19. 12 y 18

20. 12 y 54

En los Ejercicios 21-32, suma o resta las fracciones, como se indica, y simplifica tu resultado.

21. $\frac{7}{12} − \frac{1}{12}$

22. $\frac{3}{7} − \frac{5}{7}$

23. $\frac{1}{9} + \frac{1}{9}$

24. $\frac{1}{7} + \frac{3}{7}$

25. $\frac{1}{5} − \frac{4}{5}$

26. $\frac{3}{5} − \frac{2}{5}$

27. $\frac{3}{7} − \frac{4}{7}$

28. $\frac{6}{7} − \frac{2}{7}$

29. $\frac{4}{11} + \frac{9}{11}$

30. $\frac{10}{11} + \frac{4}{11}$

31. $\frac{3}{11} + \frac{4}{11}$

32. $\frac{3}{7} + \frac{2}{7}$

En los Ejercicios 33-56, suma o resta las fracciones, como se indica, y simplifica tu resultado.

33. $\frac{1}{6} − \frac{1}{8}$

34. $\frac{7}{9} − \frac{2}{3}$

35. $\frac{1}{5} + \frac{2}{3}$

36. $\frac{7}{9} + \frac{2}{3}$

37. $\frac{2}{3} + \frac{5}{8}$

38. $\frac{3}{7} + \frac{5}{9}$

39. $\frac{4}{7} − \frac{5}{9}$

40. $\frac{3}{5} − \frac{7}{8}$

41. $\frac{2}{3} − \frac{3}{8}$

42. $\frac{2}{5} − \frac{1}{8$

43. $\frac{6}{7} − \frac{1}{6}$

44. $\frac{1}{2} − \frac{1}{4}$

45. $\frac{1}{6} + \frac{2}{3}$

46. $\frac{4}{9} + \frac{7}{8}$

47. $\frac{7}{9} + \frac{1}{8}$

48. $\frac{1}{6} + \frac{1}{7}$

49. $\frac{1}{3} + \frac{1}{7}$

50. $\frac{5}{6} + \frac{1}{4}$

51. $\frac{1}{2} − \frac{2}{7}$

52. $\frac{1}{3} − \frac{1}{8}$

53. $\frac{5}{6} − \frac{4}{5}$

54. $\frac{1}{2} − \frac{1}{9}$

55. $\frac{1}{3} + \frac{1}{8}$

56. $\frac{1}{6} + \frac{7}{9}$

En los Ejercicios 57-68, sumar o restar las fracciones, como se indica, usando primero la factorización de primos para encontrar el mínimo denominador común.

57. $\frac{7}{36} + \frac{11}{54}$

58. $\frac{7}{54} + \frac{7}{24}$

59. $\frac{7}{18} − \frac{5}{12}$

60. $\frac{5}{54} − \frac{7}{12}$

61. $\frac{7}{36} + \frac{7}{54}$

62. $\frac{5}{72} + \frac{5}{108}$

63. $\frac{7}{24} − \frac{5}{36}$

64. $\frac{11}{54} + \frac{7}{72}$

65. $\frac{11}{12} + \frac{5}{18}$

66. $\frac{11}{24} + \frac{11}{108}$

67. $\frac{11}{54} − \frac{5}{24}$

68. $\frac{7}{54} − \frac{5}{24}$

En los Ejercicios 69-80, suma o resta las fracciones, como se indica, y simplifica tu resultado.

69. $\frac{−3}{7} + \left( \frac{−3}{7} \right)$

70. $\frac{−5}{9} + \left( \frac{−1}{9} \right)$

71. $\frac{7}{9} − \left( \frac{−1}{9} \right) $

72. $\frac{8}{9} − \left( \frac{−4}{9} \right)$

73. $\frac{7}{9} + \left( \frac{−2}{9} \right)$

74. $ \frac{2}{3} + \left( \frac{−1}{3} \right)$

75. $\frac{−3}{5} − \frac{4}{5}$

76. $\frac{−7}{9} − \frac{1}{9}$

77. $\frac{−7}{8} + \frac{1}{8}$

78. $\frac{−2}{3} + \(\frac{1}{3}$

79. $\frac{−1}{3} − \left( \frac{−2}{3} \right)$

80. $\frac{−7}{8} − \left( \frac{−5}{8} \right)$

En los Ejercicios 81-104, suma o resta las fracciones, como se indica, y simplifica tu resultado.

81. $\frac{−2}{7}$+\ frac {4} {5}\)

82. $\frac{−1}{4} + \frac{2}{7}$

83. $\frac{−1}{4} − \left( \frac{−4}{9} \right)$

84. $\frac{−3}{4} −left( \frac{−1}{8} \right)$

85. $\frac{−2}{7} + \frac{3}{4}$

86. $\frac{−1}{3} + \frac{5}{8}$

87. $\frac{−4}{9} − \frac{1}{3}$

88. $\frac{−5}{6} − \frac{1}{3}$

89. $\frac{−5}{7} − \left( \frac{−1}{5} \right)$

90. $\frac{−6}{7} − \left( \frac{−1}{8} \right)$

91. $\frac{1}{9} + \left( \frac{−1}{3} \right)$

92. $\frac{1}{8} + \left( \frac{−1}{2} \right)$

93. $\frac{2}{3} + \left( \frac{−1}{9} \right)$

94. $\frac{3}{4} + \left( \frac{−2}{3} \right)$

95. $\frac{−1}{2} + \left( \frac{−6}{7} \right)$

96. $\frac{−4}{5} + \left( \frac{−1}{2} \right)$

97. $\frac{−1}{2} + \left( \frac{−3}{4} \right)$

98. $\frac{−3}{5} + \left( \frac{−1}{2} \right)$

99. $\frac{−1}{4} − \frac{1}{2}$

100. $\frac{−8}{9} − \frac{2}{3}$

101. $\frac{5}{8} − \left( \frac{−3}{4} \right)$

102. $\frac{3}{4} − \left( \frac{−3}{8} \right)$

103. $\frac{1}{8} − \left( \frac{−1}{3} \right)$

104. $\frac{1}{2} − \left( \frac{−4}{9} \right)$

En Ejercicios 105-120, suma o resta las fracciones, como se indica, y escribe tu respuesta es términos más bajos.

105. $\frac{1}{2} + \frac{3q}{5}$

106. $\frac{4}{7} − \frac{b}{3}$

107. $\frac{4}{9} − \frac{3a}{4}$

108. $\frac{4}{9} − \frac{b}{2}$

109. $\frac{2}{s} + \frac{1}{3}$

110. $\frac{2}{s} + \frac{3}{7}$

111. $\frac{1}{3} − \frac{7}{b}$

112. $\frac{1}{2} − \frac{9}{s}$

113. $\frac{4b}{7} + \frac{2}{3}$

114. $\frac{2a}{5} + \frac{5}{8}$

115. $\frac{2}{3} − \frac{9}{t}$

116. $\frac{4}{7} − \frac{1}{y}$

117. $\frac{9}{s} + \frac{7}{8}$

118. $\frac{6}{t} − \frac{1}{9}$

119. $\frac{7b}{8} − \frac{5}{9}$

120. $\frac{3p}{4} − \frac{1}{8}$

En los Ejercicios 121-132, determinar cuál de las dos afirmaciones dadas es verdadera.

121. $\frac{−2}{3} < \frac{−8}{7}$o$\frac{− 2}{3} > \frac{−8}{7}$

122. $\frac{−1}{7} < \frac{−8}{9}$o$\frac{− 1}{7} > \frac{−8}{9}$

123. $\frac{6}{7} < \frac{7}{3}$o$\frac{6}{7} > \frac{7}{3}$

124. $\frac{1}{2} < \frac{2}{7}$o$\frac{1}{2} > \frac{2}{7}$

125. $\frac{−9}{4} < \frac{−2}{3}$o\ frac {− 9} {4} >\ frac {−2} {3}\)

126. $\frac{−3}{7} < \frac{−9}{2}$o$\frac{− 3}{7} > \frac{−9}{2}$

127. $\frac{5}{7} < \frac{5}{9}$o\ frac {5} {7} >\ frac {5} {9}\)

128. $\frac{1}{2} < \frac{1}{3}$o$\frac{1}{2} > \frac{1}{3}$

129. $\frac{−7}{2} < \frac{−1}{5}$o$\frac{− 7}{2} > \frac{−1}{5}$

130. $\frac{−3}{4} < \frac{−5}{9}$o$\frac{− 3}{4} > \frac{−5}{9}$

131. $\frac{5}{9} < \frac{6}{5}$o$\frac{5}{9} > \frac{6}{5}$

132. $\frac{3}{2} < \frac{7}{9}$o$\frac{3}{2} > \frac{7}{9}$

RESPUESTAS

1. 45

3. 40

5. 80

7. 60

9. 30

11. 108

13. 72

15. 216

17. 72

19. 36

21. $\frac{1}{2}$

23. $\frac{2}{9}$

25. $\frac{−3}{5}$

27. $\frac{−1}{7}$

29. $\frac{13}{11}$

31. $\frac{7}{11}$

33. $\frac{1}{24}$

35. $\frac{13}{15}$

37. $\frac{31}{24}$

39. $\frac{1}{63}$

41. $\frac{7}{24}$

43. $\frac{29}{42}$

45. $\frac{5}{6}$

47. $\frac{65}{72}$

49. $\frac{10}{21}$

51. $\frac{3}{14}$

53. $\frac{1}{30}$

55. $\frac{11}{24}$

57. $\frac{43}{108}$

59. $\frac{−1}{36}$

61. $\frac{35}{108}$

63. $\frac{11}{72}$

65. $\frac{43}{36}$

67. $\frac{−1}{216}$

69. $\frac{−6}{7}$

71. $\frac{8}{9}$

73. $\frac{5}{9}$

75. $\frac{− 7}{5}$

77. $\frac{− 3}{4}$

79. $\frac{1}{3}$

81. $\frac{18}{35}$

83. $\frac{7}{36}$

85. $\frac{13}{28}$

87. $\frac{− 7}{9}$

89. $\frac{−18}{35}$

91. $\frac{− 2}{9}$

93. $\frac{5}{9}$

95. $\frac{−19}{14}$

97. $\frac{− 5}{4}$

99. $\frac{− 3}{4}$

101. $\frac{11}{8}$

103. $\frac{11}{24}$

105. $\frac{5+6 q}{10}$

107. $\frac{16 − 27 a}{36}$

109. $\frac{6 + s}{3 s}$

111. $\frac{b − 21}{3b}$

113. $\frac{12 b + 14}{21}$

115. $\frac{2 t − 27}{3t}$

117. $\frac{72 + 7 s}{8 s}$

119. $\frac{63 b − 40}{72}$

121. $\frac{− 2}{3} > \(\frac{− 8}{7}$

123. $\frac{6}{7} < \frac{7}{3}$

125. $\frac{− 9}{4} < \frac{− 2}{3}$

127. $\frac{5}{7} > \frac{5}{9}$

129. $\frac{− 7}{2 } < \frac{− 1}{5}$

131. $\frac{5}{9} < \frac{6}{5}$

Search

Text Color

Text Size

Margin Size

Font Type