Saltar al contenido principal
LibreTexts Español

1.E: Números Enteros (Ejercicios)

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    114225

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    1.1 - Introducción a los números enteros

    Identificar números de conteo y números enteros

    En los siguientes ejercicios, determinar cuáles de los siguientes números son (a) contando números (b) números enteros.

    1. 0, 2, 99
    2. 0, 3, 25
    3. 0, 4, 90
    4. 0, 1, 75

    Números enteros del modelo

    En los siguientes ejercicios, modele cada número usando bloques base-10 y luego muestre su valor usando notación de valor posicional.

    1. 258
    2. 104

    Identificar el valor posicionar de un dígito

    En los siguientes ejercicios, encuentra el valor posicional de los dígitos dados.

    1. 472,981

    a) 8 b) 4 c) 1 d) 7 e) 2

    1. 12,403,295

    (a) 4 (b) 0 (c) 1 (d) 9 (e) 3

    Usar el valor positorio para nombrar números enteros

    En los siguientes ejercicios, nombra cada número en palabras.

    1. 5,280
    2. 204,614
    3. 5,012,582
    4. 31,640,976

    Usar valor posicionar para escribir números enteros

    En los siguientes ejercicios, escribe cada número como un número entero usando dígitos.

    1. seiscientos dos
    2. quince mil doscientos cincuenta y tres
    3. trescientos cuarenta millones novecientos doce mil sesenta y uno
    4. dos mil millones, cuatrocientos noventa y dos millones, setecientos once mil, dos

    Números Redondos Enteros

    En los siguientes ejercicios, redondea al diez más cercano.

    1. 412
    2. 648
    3. 3,556
    4. 2,734

    En los siguientes ejercicios, redondea al centenar más cercano.

    1. 38,975
    2. 26,849
    3. 81,486
    4. 75,992

    1.2 - Agregar números enteros

    Usar notación de adición

    En los siguientes ejercicios, traduzca lo siguiente de la notación matemática a las palabras.

    1. 4 + 3
    2. 25 + 18
    3. 571 + 629
    4. 10,085 + 3,492

    Adición de modelos de números enteros

    En los siguientes ejercicios, modelar la adición.

    1. 6 + 7
    2. 38 + 14

    Agregar números enteros

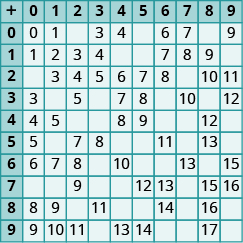
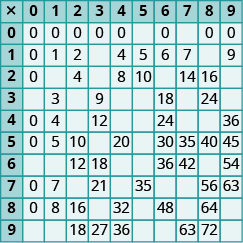
    En los siguientes ejercicios, rellena los valores que faltan en cada gráfico.

    1. Una mesa con 11 filas hacia abajo y 11 filas de ancho. La primera fila y la primera columna son encabezados e incluyen los números del 0 al 9 tanto a través como hacia abajo, con un signo más en la primera celda. Los números cruzados en la segunda fila hacia abajo aparecen de la siguiente manera: 0,0, 1, nulo, 3, 4, nulo, 6, 7, nulo, 9. Los números cruzados en la tercera fila hacia abajo aparecen de la siguiente manera: 1, 1, 2, 3, 4, nulo, nulo, 7, 8, 9, nulo. Los números en la cuarta fila hacia abajo aparecen de la siguiente manera: 2, null, 3, 4, 5, 6, 7, 8, 8, 8, null, 10, 11. Los números cruzados en la quinta fila hacia abajo aparecen de la siguiente manera: 3, 3, nulo, 5, nulo, 7, 8, nulo, 10, nulo 12. Los números cruzados en la sexta fila hacia abajo aparecen de la siguiente manera: 4, 4, 5, nulo, nulo, 8, 9, nulo, nulo, 12, nulo. Los números cruzados en la séptima fila hacia abajo aparecen de la siguiente manera: 5, 5, nulo, 7, 8, nulo nulo, 11, nulo, 13, nulo. Los números cruzados en la octava fila hacia abajo aparecen de la siguiente manera: 6, 6, 7, 8, nulo, 10, nulo, nulo, 13, nulo, 15. Los números cruzados en la novena fila hacia abajo aparecen de la siguiente manera: nulo, nulo, 9, nulo, nulo, 12, 13, nulo, 15, 16. Los números cruzados en la décima fila hacia abajo aparecen de la siguiente manera: 8,8,9, nulos, 11, nulos, nulos, 14, nulos, undécima fila abajo aparecen de la siguiente manera: 9, 9, 10, 11, nulo, 13, 14, nulo, nulo, 17, nulo.
    2. Esta tabla es de 5 filas y 8 columnas. La fila superior es una fila de encabezado e incluye los números del 3 al 9, un número para cada celda. Las filas hacia abajo incluyen 6, 7, 8 y 9. Hay un signo más en la primera celda. Todas las celdas son nulas.

    En los siguientes ejercicios, agregue.

    1. (a) 0 + 19 (b) 19 + 0
    2. (a) 0 + 480 (b) 480 + 0
    3. (a) 7 + 6 (b) 6 + 7
    4. (a) 23 + 18 (b) 18 + 23
    5. 44 + 35
    6. 63 + 29
    7. 96 + 58
    8. 375 + 591
    9. 7,281 + 12,546
    10. 5,280 + 16,324 + 9,731

    Traducir frases de palabras a notación matemática

    En los siguientes ejercicios, traduzca cada frase a notación matemática y luego simplifique.

    1. la suma de 30 y 12
    2. 11 aumentado en 8
    3. 25 más de 39
    4. total de 15 y 50

    Agregar números enteros en aplicaciones

    En los siguientes ejercicios, resuelve.

    1. Al comprar una entrevista Nathan compró una camisa, corbata y pantalones nuevos para usar en una entrevista de trabajo. La camisa costó 24 dólares, la corbata 14 dólares y los pantalones 38 dólares. ¿Cuál fue el costo total de Nathan?
    2. Correr Jackson corrió 4 millas el lunes, 12 millas el martes, 1 milla el miércoles, 8 millas el jueves y 5 millas el viernes. ¿Cuál fue el número total de millas que Jackson corrió?

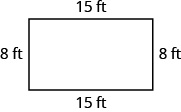
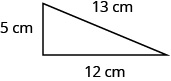
    En los siguientes ejercicios, encuentra el perímetro de cada figura.

    1. Una imagen de un rectángulo que mide 8 pies de alto y 15 pies de ancho.
    2. Imagen de un triángulo rectángulo que tiene una base de 12 centímetros, una altura de 5 centímetros, y una hipotenusa diagonal de 13 centímetros.

    1.3 - Restar números enteros

    Usar notación de resta

    En los siguientes ejercicios, traduzca lo siguiente de la notación matemática a las palabras.

    1. 14 − 5
    2. 40 − 15
    3. 351 − 249
    4. 5,724 − 2,918

    Modelo de resta de números enteros

    En los siguientes ejercicios, modele la resta.

    1. 18 − 4
    2. 41 − 29

    Restar números enteros

    En los siguientes ejercicios, restar y luego verificar sumando.

    1. 8 − 5
    2. 12 − 7
    3. 23 − 9
    4. . 46 − 21
    5. 82 − 59
    6. 110 − 87
    7. 539 − 217
    8. 415 − 296
    9. 1,020 − 640
    10. 8,355 − 3,947
    11. 10,000 − 15
    12. 54,925 − 35,647

    Traducir frases de palabras a notación matemática

    En los siguientes ejercicios, traduzca y simplifique.

    1. la diferencia de diecinueve y trece
    2. restar sesenta y cinco de cien
    3. setenta y cuatro disminuyeron en ocho
    4. veintitrés menos de cuarenta y uno

    Restar números enteros en aplicaciones

    En los siguientes ejercicios, resuelve.

    1. Temperatura La temperatura alta en Peoria un día fue de 86 grados Fahrenheit y la temperatura baja fue de 28 grados Fahrenheit. ¿Cuál fue la diferencia entre las temperaturas altas y bajas?
    2. Ahorros Lynn quiere ir en un crucero que cuesta $2,485. Tiene 948 dólares en su cuenta de ahorro vacacional. ¿Cuánto más necesita ahorrar para poder pagar el crucero?

    1.4 - Multiplicar números enteros

    Usar notación de multiplicación

    En los siguientes ejercicios, traduzca de la notación matemática a las palabras.

    1. 8 × 5
    2. 6 • 14
    3. (10) (95)
    4. 54 (72)

    Modelo de multiplicación de números enteros

    En los siguientes ejercicios, modelar la multiplicación.

    1. 2 × 4
    2. 3 × 8

    Multiplicar números enteros

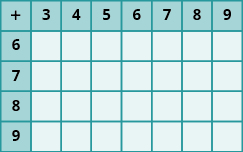
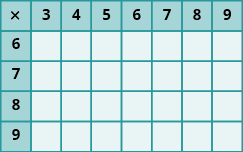
    En los siguientes ejercicios, rellena los valores que faltan en cada gráfico.

    1. Una mesa con 10 filas hacia abajo y 10 filas de ancho. La primera fila y la primera columna son encabezados e incluyen los números del 0 al 9 tanto a través como hacia abajo, con un signo más en la primera celda. Los números cruzados en la segunda fila hacia abajo aparecen de la siguiente manera: 0, 0, 0, 0, 0, nulo, 0, nulo, 0,0. Los números cruzados en la tercera fila hacia abajo aparecen de la siguiente manera: 1, 0, 1, 2, nulo, 4, 5, 6, 7, nulo, 9. Los números cruzados en la cuarta fila hacia abajo aparecen de la siguiente manera: 2, 0, nulo, 4, nulo, 8, 10, nulo, 14, 16, nulo. Los números cruzados en la quinta fila hacia abajo aparecen de la siguiente manera: 3, nulo, 3, nulo, 9, nulo, nulo, 18, nulo, 24, nulo. Los números cruzados en la sexta fila hacia abajo aparecen de la siguiente manera: 4, 0, 4, 0, 12, nulo, nulo, 24, nulo, nulo, 36. Los números cruzados en la séptima fila hacia abajo aparecen de la siguiente manera: 5, 0, 5, 10, nulo, 20, nulo, 30, 35, 40, 45. Los números cruzados en la octava fila hacia abajo aparecen de la siguiente manera: 6, nulo, nulo, 12, 18, nulo, nulo, 36, 42, nulo, 54. Los números cruzados en la novena fila hacia abajo aparecen de la siguiente manera: 7, 0, 7, nulo, 21, nulo, 35, nulo, nulo, 56, 63. Los números en la décima fila hacia abajo aparecen de la siguiente manera: 8, 0, 8, 16, nulo, 32, nulo, 48, nulo, 64, nulo. Los números en la undécima fila hacia abajo aparecen de la siguiente manera: 9, nulo, nulo, 18, 27, 36, nulo, nulo, 63, 72, nulo.
    2. Imagen de una mesa con 8 columnas y 5 filas. Las celdas de la primera fila y la primera columna están sombreadas más oscuras que las otras celdas. La primera fila tiene los valores “x; 3; 4; 5; 6; 7; 8; 9”. La primera columna tiene los valores “x; 6; 7; 8; 9”. Todas las demás celdas son nulas.

    En los siguientes ejercicios, multiplicar.

    1. 0 • 14
    2. (256) 0
    3. 1 • 99
    4. (4,789) 1
    5. (a) 7 • 4 (b) 4 • 7
    6. (25) (6)
    7. 9,261 × 3
    8. 48 • 76
    9. 64 • 10
    10. 1,000 (22)
    11. 162 × 493
    12. (601) (943)
    13. 3,624 × 517
    14. 10,538 • 22

    Traducir frases de palabras a notación matemática

    En los siguientes ejercicios, traduzca y simplifique.

    1. el producto de 15 y 28
    2. noventa y cuatro veces treinta y tres
    3. dos veces 575
    4. diez por doscientos sesenta y cuatro

    Multiplicar números enteros en aplicaciones

    En los siguientes ejercicios, resuelve.

    1. Jardinería Geniece compró 8 paquetes de caléndulas para plantar en su patio. Cada paquete tiene 6 flores. ¿Cuántas caléndulas compró Geniece?
    2. Cocinar Ratika es hacer arroz para una cena. El número de tazas de agua es el doble del número de tazas de arroz. Si Ratika planea usar 4 tazas de arroz, ¿cuántas tazas de agua necesita?
    3. Multiplex Hay doce teatros en el multiplex y cada teatro tiene 150 asientos. ¿Cuál es el número total de asientos en el multiplex?
    4. Techos Lewis necesita poner tejas nuevas en su techo. El techo es un rectángulo, 30 pies por 24 pies. ¿Cuál es el área del techo?

    1.5 - Dividir números enteros

    Usar notación de división

    Traducir de la notación matemática a las palabras.

    1. 54 ÷ 9
    2. 42/7
    3. \(\dfrac{72}{8}\)
    4. \(6 \overline{\smash{)}48}\)

    División Modelo de Números Enteros

    En los siguientes ejercicios, modelar.

    1. 8 ÷ 2
    2. \(3 \overline{\smash{)}12}\)

    Dividir números enteros

    En los siguientes ejercicios, divide. Después verifica multiplicando.

    1. 14 ÷ 2
    2. \(\dfrac{32}{8}\)
    3. 52 ÷ 4
    4. \(26 \overline{\smash{)}26}\)
    5. \(\dfrac{97}{1}\)
    6. 0 ÷ 52
    7. 100 ÷ 0
    8. \(\dfrac{355}{5}\)
    9. 3828 ÷ 6
    10. \(31 \overline{\smash{)}1,519}\)
    11. \(\dfrac{7505}{25}\)
    12. 5,166 ÷ 42

    Traducir frases de palabras a notación matemática

    En los siguientes ejercicios, traduzca y simplifique.

    1. el cociente de 64 y 16
    2. el cociente de 572 y 52

    Dividir números enteros en aplicaciones

    En los siguientes ejercicios, resuelve.

    1. Cinta Un carrete de cinta mide 27 pies. Lizbeth usa 3 pies de cinta por cada canasta de regalo que envuelve. ¿Cuántas canastas de regalo puede envolver Lizbeth de un carrete de cinta?
    2. Jugo Una caja de jugo de fruta es de 128 onzas. ¿Cuántas tazas de 4 onzas puede llenar Shayla de una caja de jugo?

    PRUEBA DE PRÁCTICA

    1. Determine cuáles de los siguientes números son (a) contando números (b) números enteros. $$0, 4, 87$$
    2. Encuentra el valor posicional de los dígitos dados en el número 549,362.

    a) 9 b) 6 c) 2 d) 5

    1. Escribe cada número como un número entero usando dígitos.

    a) seiscientos trece b) cincuenta y cinco mil doscientos ocho

    1. Vuelta 25,849 al cien más cercano.

    Simplificar.

    1. 45 + 23
    2. 65 − 42
    3. 85 ÷ 5
    4. 1,000 × 8
    5. 90 − 58
    6. 73 + 89
    7. (0) (12,675)
    8. 634 + 255
    9. \(\dfrac{0}{9}\)
    10. \(8 \overline{\smash{)}128}\)
    11. 145 − 79
    12. 299 + 836
    13. 7 • 475
    14. 8,528 + 704
    15. 35 (14)
    16. \(\dfrac{26}{0}\)
    17. 733 − 291
    18. 4,916 − 1,538
    19. 495 ÷ 45
    20. 52 × 983

    Traduzca cada frase a notación matemática y luego simplifique.

    1. La suma de 16 y 58
    2. El producto de 9 y 15
    3. La diferencia de 32 y 18
    4. El cociente de 63 y 21
    5. Dos veces 524
    6. 29 más de 32
    7. 50 menos de 300

    En los siguientes ejercicios, resuelve.

    1. LaVelle compra una bolsa jumbo de 84 caramelos para hacer bolsas de favor para la fiesta de su hijo. Si quiere hacer 12 bolsas, ¿cuántos caramelos debe poner en cada bolsa?
    2. El mes pasado, el pago para llevar a casa de Stan fue de $3,816 y sus gastos fueron de $3,472. ¿Cuánto de su paga para llevar a casa le quedaba a Stan después de pagar sus gastos?
    3. Cada clase en Greenville School cuenta con 22 niños matriculados. La escuela cuenta con 24 clases. ¿Cuántos niños están matriculados en Greenville School?
    4. Clayton caminó 12 cuadras hasta la casa de su madre, 6 cuadras hasta el gimnasio y 9 cuadras hasta la tienda de abarrotes antes de caminar las últimas 3 cuadras a casa. ¿Cuál fue el número total de cuadras que Clayton caminó?

    Colaboradores y Atribuciones

    This page titled 1.E: Números Enteros (Ejercicios) is shared under a not declared license and was authored, remixed, and/or curated by OpenStax.