1.8: Multiplicar números enteros (Parte 2)
- Page ID
- 114210
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Traducir frases de palabras a notación matemática
Anteriormente en esta sección, traducimos la notación matemática en palabras. Ahora invertiremos el proceso y traduciremos frases de palabras a notación matemática. Algunas de las palabras que indican multiplicación se dan en Tabla\(\PageIndex{3}\).
| Operación | Frase de palabras | Ejemplo | Expresión |
|---|---|---|---|
| Multiplicación | tiempos | 3 times 8 | 3 × 8, 3 • 8, (3) (8), |
| producto | el producto de 3 y 8 | (3) 8, o 3 (8) | |
| dos veces | dos veces 4 | 2 • 4 |
Traducir y simplificar: el producto de\(12\) y\(27\).
Solución
La palabra producto nos dice que nos multipliquemos. Las palabras de\(12\) y\( 27\) nos dicen los dos factores.
| el producto de 12 y 27 | |
| Traducir. | 12 • 27 |
| Multiplicar. | 324 |
Traducir y simplificar el producto de\(13\) y\(28\).
- Contestar
-
\(13 · 28\);\(364\)
Traducir y simplificar el producto de\(47\) y\(14\).
- Contestar
-
\(47 · 14\);\(658\)
Traducir y simplificar: dos veces doscientos once.
Solución
La palabra dos veces nos dice que multipliquemos por\(2\).
| dos veces doscientos once | |
| Traducir. | 2 (211) |
| Multiplicar. | 422 |
Traducir y simplificar: dos veces ciento sesenta y siete.
- Contestar
-
\(2(167)\);\(334\)
Traducir y simplificar: dos veces doscientos cincuenta y ocho.
- Contestar
-
\(2(258)\);\(516\)
Multiplicar números enteros en aplicaciones
Utilizaremos la misma estrategia que antes usábamos para resolver aplicaciones de multiplicación. Primero, tenemos que determinar lo que estamos buscando. Entonces escribimos una frase que da la información para encontrarla. Luego traducimos la frase a notación matemática y simplificamos para obtener la respuesta. Por último, escribimos una frase para responder a la pregunta.
Humberto compró\(4\) hojas de sellos. Cada hoja tenía\(20\) sellos. ¿Cuántos sellos compró Humberto?
Solución
Se nos pide encontrar el número total de sellos.
| Escribe una frase para el total. | el producto de 4 y 20 |
| Traducir a notación matemática. | 4 • 20 |
| Multiplicar. |  |
| Escribe una oración para responder a la pregunta. | Humberto compró 80 sellos. |
Valia donó agua para el snack bar en el juego de béisbol de su hijo. Ella trajo\(6\) cajas de botellas de agua. Cada caja tenía botellas\(24\) de agua. ¿Cuántas botellas de agua donó Valia?
- Contestar
-
Valia donó botellas de\(144\) agua.
Vanessa trajo\(8\) paquetes de perritos calientes a una reunión familiar. Cada paquete tiene perritos\(10\) calientes. ¿Cuántos perritos calientes trajo Vanessa?
- Contestar
-
Vanessa compró perritos\(80\) calientes.
Cuando Rena cocina el arroz, usa el doble de agua que el arroz. ¿Cuánta agua necesita para cocinar\(4\) tazas de arroz?
Solución
Se nos pide que encontremos cuánta agua necesita Rena.
| Escribir como frase. | el doble de 4 tazas |
| Traducir a notación matemática. | 2 • 4 |
| Multiplicar para simplificar. | 8 |
| Escribe una oración para responder a la pregunta. | Rena necesita 8 tazas de agua para tazas de arroz. |
Erin está planeando su jardín de flores. Ella quiere plantar el doble de dalias que girasoles. Si planta\(14\) girasoles, ¿cuántas dalias necesita?
- Contestar
-
Erin necesita\(28\) dalias.
Un coro universitario tiene el doble de mujeres que de hombres. Hay\(18\) hombres en el coro. ¿Cuántas mujeres hay en el coro?
- Contestar
-
Hay\(36\) mujeres en el coro.
Van planea construir un patio. Tendrá\(8\) filas de azulejos, con\(14\) azulejos en cada fila. ¿Cuántos azulejos necesita para el patio?
Solución
Se nos pide encontrar el número total de mosaicos.
| Escribir como frase. | el producto de 8 y 14 |
| Traducir a notación matemática. | 8 • 14 |
| Multiplicar para simplificar. | 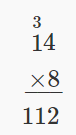 |
| Escribe una oración para responder a la pregunta. | Van necesita 112 azulejos para su patio. |
Jane está embaldosando el piso de su sala de estar. Ella necesitará\(16\) filas de baldosas, con\(20\) azulejos en cada fila. ¿Cuántos azulejos necesita para el piso de la sala?
- Contestar
-
Jane necesita\(320\) azulejos.
Yousef está poniendo tejas en el techo de su cochera. Necesitará\(24\) filas de tejas, con\(45\) tejas en cada fila. ¿Cuántas tejas necesita para el techo de la cochera?
- Contestar
-
Yousef necesita\(1,080\) azulejos.
Si queremos saber el tamaño de una pared que necesita ser pintada o un piso que necesita ser alfombrado, necesitaremos encontrar su área. El área es una medida de la cantidad de superficie que está cubierta por la forma. El área se mide en unidades cuadradas. A menudo usamos pulgadas cuadradas, pies cuadrados, centímetros cuadrados o millas cuadradas para medir el área. Un centímetro cuadrado es un cuadrado que es de un centímetro (cm.) en un lado. Una pulgada cuadrada es un cuadrado que es una pulgada en cada lado, y así sucesivamente.
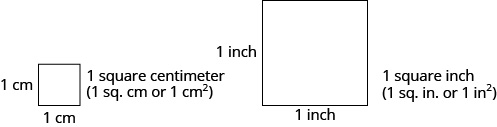
Figura\(\PageIndex{2}\)
Para una figura rectangular, el área es producto de la longitud y la anchura. La figura\(\PageIndex{3}\) muestra una alfombra rectangular con un largo de\(2\) pies y un ancho de\(3\) pies. Cada cuadrado es de\(1\) pie de ancho por\(1\) pie de largo, o pie\(1\) cuadrado. La alfombra está hecha de\(6\) cuadrados. El área de la alfombra es de pies\(6\) cuadrados.
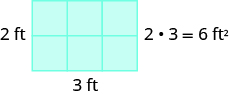
Figura\(\PageIndex{3}\): El área de un rectángulo es producto de su longitud y su anchura, o 6 pies cuadrados.
El techo de la cocina de Jen es un rectángulo que mide\(9\) pies de largo por\(12\) pies de ancho. ¿Cuál es el área del techo de la cocina de Jen?
Solución
Se nos pide encontrar el área del techo de la cocina.
| Escribir como frase. | el producto de 9 y 12 |
| Traducir a notación matemática. | 9 • 12 |
| Multiplicar para simplificar. | 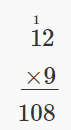 |
| Escribe una oración para responder a la pregunta. | El área del techo de la cocina de Jen es de 108 pies cuadrados. |
Zoila compró una alfombra rectangular. La alfombra mide\(8\) pies de largo por\(5\) pies de ancho. ¿Cuál es el área de la alfombra?
- Contestar
-
El área de la alfombra es de pies\(40\) cuadrados.
El camino de entrada de René es un rectángulo\(45\) pies de largo por\(20\) pies de ancho. ¿Cuál es la zona del camino de entrada?
- Contestar
-
El área de la entrada es de pies\(900\) cuadrados
Acceda a recursos adicionales en línea
Conceptos clave
| Operación | Notación | Expresión | Leer como | Resultado |
|---|---|---|---|---|
- Propiedad de multiplicación de cero
- El producto de cualquier número y\(0\) es\(0\).
- El producto de cualquier número y\(0\) es\(0\).
- Identidad Propiedad de la Multiplicación
- El producto de cualquier número y\(1\) es el número.
- El producto de cualquier número y\(1\) es el número.
- Propiedad conmutativa de la multiplicación
- Cambiar el orden de los factores no cambia su producto.
- Cambiar el orden de los factores no cambia su producto.
- Multiplica dos números enteros para encontrar el producto.
- Escribe los números para que cada valor posicional se aleje verticalmente.
- Multiplique los dígitos en cada valor posicional.
- Trabajar de derecha a izquierda, comenzando por los que se colocan en el número inferior.
- Multiplique el número inferior por el dígito unos en el número superior, luego por el dígito de las decenas, y así sucesivamente.
- Si un producto en un valor posicional es mayor que\(9\), lleve al siguiente valor posicional.
- Escribe los productos parciales, alineando los dígitos en los valores posicionados con los números anteriores. Repita para el lugar de las decenas en el número inferior, el lugar de los cientos, y así sucesivamente.
- Inserte un cero como marcador de posición con cada producto parcial adicional.
- Agregar los productos parciales.
Glosario
- producto
-
El producto es el resultado de multiplicar dos o más números.
La práctica hace la perfección
Usar notación de multiplicación
En los siguientes ejercicios, traduzca de la notación matemática a las palabras.
- 4 × 7
- 8 × 6
- 5 • 12
- 3 • 9
- (10) (25)
- (20) (15)
- 42 (33)
- 39 (64)
Modelo de multiplicación de números enteros
En los siguientes ejercicios, modelar la multiplicación.
- 3 × 6
- 4 × 5
- 5 × 9
- 3 × 9
Multiplicar números enteros
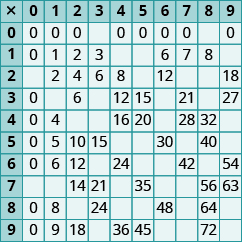
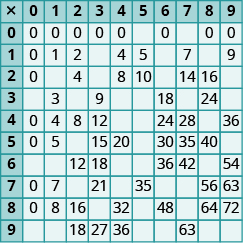
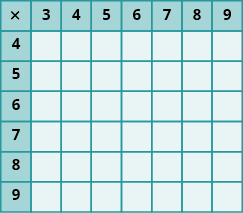
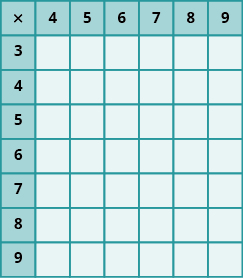
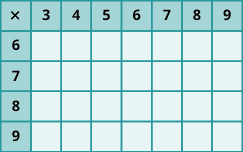
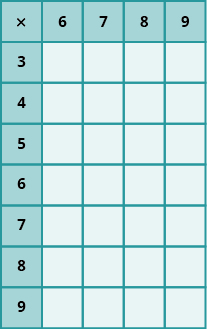
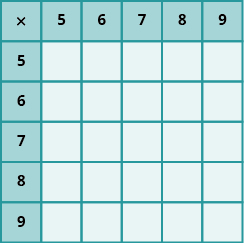
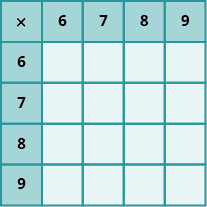
En los siguientes ejercicios, rellena los valores que faltan en cada gráfico.
En los siguientes ejercicios, multiplicar.
- 0 • 15
- 0 • 41
- (99) 0
- (77) 0
- 1 • 43
- 1 • 34
- (28) 1
- (65) 1
- 1 (240,055)
- 1 (189,206)
- (a) 7 • 6 (b) 6 • 7
- (a) 8 × 9 (b) 9 × 8
- (79) (5)
- (58) (4)
- 275 • 6
- 638 • 5
- 3,421 × 7
- 9,143 × 3
- 52 (38)
- 37 (45)
- 96 • 73
- 89 • 56
- 27 × 85
- 53 × 98
- 23 • 10
- 19 • 10
- (100) (36)
- (100) (25)
- 1,000 (88)
- 1,000 (46)
- 50 × 1,000,000
- 30 × 1,000,000
- 247 × 139
- 156 × 328
- 586 (721)
- 472 (855)
- 915 • 879
- 968 • 926
- (104) (256)
- (103) (497)
- 348 (705)
- 485 (602)
- 2,719 × 543
- 3,581 × 724
Traducir frases de palabras a notación matemática
En los siguientes ejercicios, traduzca y simplifique.
- el producto de 18 y 33
- el producto de 15 y 22
- cincuenta y uno por sesenta y siete
- cuarenta y ocho por setenta y uno
- dos veces 249
- dos veces 589
- diez por trescientos setenta y cinco
- diez por doscientos cincuenta y cinco
Práctica Mixta
En los siguientes ejercicios, simplifique.
- 38 × 37
- 86 × 29
- 415 − 267
- 341 − 285
- 6,251 + 4,749
- 3,816 + 8,184
- (56) (204)
- (77) (801)
- 947 • 0
- 947 + 0
- 15,382 + 1
- 15,382 • 1
En los siguientes ejercicios, traduzca y simplifique.
- la diferencia de 50 y 18
- la diferencia de 90 y 66
- dos veces 35
- dos veces 140
- 20 más de 980
- 65 más de 325
- el producto de 12 y 875
- el producto de 15 y 905
- restar 74 de 89
- restar 45 de 99
- la suma de 3,075 y 950
- la suma de 6,308 y 724
- 366 menos de 814
- 388 menos de 925
Multiplicar números enteros en aplicaciones
En los siguientes ejercicios, resuelve.
- Suministros para fiestas Tim trajo 9 paquetes de seis refresco a una fiesta en un club. ¿Cuántas latas de refresco trajo Tim?
- Coser Kanisha es hacer una colcha. Ella compró 6 tarjetas de botones. Cada tarjeta tenía cuatro botones en ella. ¿Cuántos botones compró Kanisha?
- Excursión Siete autobuses escolares dejan salir a sus alumnos frente a un museo en Washington, DC. Cada autobús escolar contaba con 44 alumnos. ¿Cuántos alumnos había?
- Jardinería Kathryn compró 8 pisos de impatiens para su lecho de flores. Cada piso tiene 24 flores. ¿Cuántas flores compró Kathryn?
- Charity Rey donó 15 doce paquetes de camisetas a un refugio para personas sin hogar. ¿Cuántas playeras donó?
- Escuela Hay 28 aulas en la escuela primaria Anna C. Scott. Cada aula cuenta con 26 escritorios para estudiantes. ¿Cuál es el número total de escritorios de estudiantes?
- Receta Stephanie está haciendo ponche para una fiesta. En la receta se pide el doble de jugo de frutas que el refresco club. Si usa 10 tazas de refresco club, ¿cuánto jugo de frutas debe usar?
- Jardinería Hiroko está poniendo en un huerto. Quiere tener el doble de plantas de lechuga que las plantas de tomate. Si compra 12 plantas de tomate, ¿cuántas plantas de lechuga debería obtener?
- Gobierno El Senado de Estados Unidos tiene el doble de senadores que estados en Estados Unidos. Hay 50 estados. ¿Cuántos senadores hay en el Senado de Estados Unidos?
- Receta Andrea está haciendo ensalada de papa para un almuerzo buffet. La receta dice que el número de porciones de ensalada de papa será el doble del número de libras de papa. Si compra 30 libras de papas, ¿cuántas porciones de ensalada de papa habrá?
- Pintar a Jane es pintar una pared de su sala de estar. La pared es rectangular, 13 pies de ancho por 9 pies de alto. ¿Cuál es el área de la pared?
- La decoración del hogar Shawnte compró una alfombra para el salón de su departamento. La alfombra mide 3 pies de ancho por 18 pies de largo. ¿Cuál es el área de la alfombra?
- Tamaño de la habitación La sala de reuniones en un centro para personas mayores es rectangular, con longitud 42 pies y ancho 34 pies. ¿Cuál es el área de la sala de reuniones?
- Jardinería June tiene un huerto en su patio. El jardín es rectangular, con longitud 23 pies y ancho 28 pies. ¿Cuál es la zona del jardín?
- Basquetbol de la NCAA Según la normativa de la NCAA, las dimensiones de una cancha rectangular de basquetbol deben ser de 94 pies por 50 pies. ¿Cuál es el área de la cancha de basquetbol?
- Fútbol de la NCAA De acuerdo con la normativa de la NCAA, las dimensiones de un campo de fútbol rectangular deben ser de 360 pies por 160 pies. ¿Cuál es el área del campo de fútbol?
Matemáticas cotidianas
- Bolsa Javier posee 300 acciones de acciones en una sola compañía. El martes, el precio de las acciones subió 12 dólares por acción. ¿Cuánto dinero ganó la cartera de Javier?
- Sueldo Carlton obtuvo un aumento de $200 en cada cheque de pago. Se le paga 24 veces al año. ¿Cuánto más alto es su nuevo sueldo anual?
Ejercicios de escritura
- ¿Qué tan seguro se siente acerca de su conocimiento de los hechos de multiplicación? Si no tienes plena confianza, ¿qué harás para mejorar tus habilidades?
- ¿Cómo has usado modelos para ayudarte a conocer los hechos de la multiplicación?
Autocomprobación
(a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.
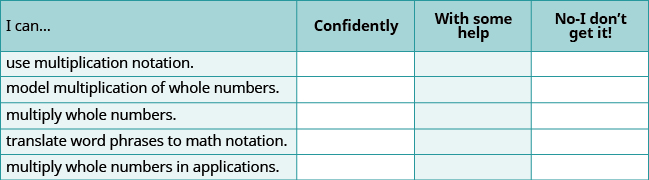
b) En una escala del 1 al 10, ¿cómo calificaría su dominio de esta sección a la luz de sus respuestas en la lista de verificación? ¿Cómo se puede mejorar esto?