1.S: Números Enteros (Resumen)

Última actualización
Guardar como PDF

Page ID: 114215

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Términos Clave

coordinar	Un número emparejado con un punto en una recta numérica.
contar números	Los números de conteo son los números 1, 2, 3,...
diferencia	El resultado de restar dos o más números.
dividendo	El número se divide al dividir dos números.
divisor	El número que divide el dividendo al dividir dos números.
línea numérica*	Se utiliza una línea numérica para visualizar números. Los números en la recta numérica se hacen más grandes a medida que van de izquierda a derecha, y más pequeños a medida que van de derecha a izquierda.
origen	El punto etiquetado como 0 en una recta numérica.
sistema de valor posicionar	Nuestro sistema numérico se llama sistema de valor posicional porque el valor de un dígito depende de su posición, o lugar, en un número.
producto	El resultado de multiplicar dos o más números.
cociente	El resultado de dividir dos números.
redondeo	El proceso de aproximación de un número.
suma	El resultado de sumar dos o más números.
números enteros	Los números enteros son los números 0, 1, 2, 3,...

Conceptos clave

1.1 - Introducción a los números enteros

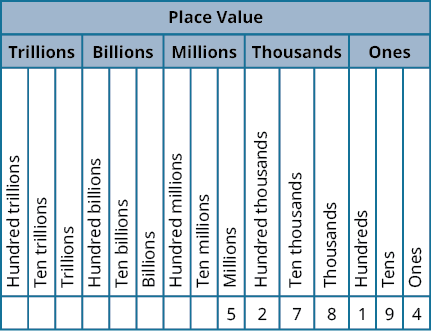
$Un gráfico titulado 'Valor posible' con quince columnas y 4 filas, con las columnas divididas en cinco grupos de tres. La fila de encabezado muestra Trillones, Miles de millones, millones, miles y unos. La siguiente fila tiene los valores 'Cien trillones', 'Diez trillones', 'billones', 'cien mil millones', 'diez mil millones', 'mil millones', 'cien millones', 'diez millones', 'millones', 'cien miles', 'diez miles', 'miles', 'cientos', 'decenas', y 'unos'. Los primeros 8 valores de la siguiente fila están en blanco. A partir de la novena columna, los valores son '5', '2', '7', '8', '1', '9' y '4'.$

Nombra un número entero en palabras.
1. Comenzando por el dígito de la izquierda, nombra el número en cada periodo, seguido del nombre del período. No incluya el nombre del período para los.
2. Use comas en el número para separar los puntos.
Usa el valor posicionar para escribir un número entero.
1. Identificar las palabras que indican periodos. (Recuerde que el período de unos nunca se nombra.)
2. Dibuja tres espacios en blanco para indicar el número de lugares necesarios en cada periodo.
3. Nombra el número en cada periodo y coloca los dígitos en la posición correcta del valor posicional.
Redondear un número entero a un valor posicional específico.
1. Localizar el valor positorio dado. Todos los dígitos a la izquierda de ese valor posicional no cambian.
2. Subrayar el dígito a la derecha del valor posicional dado.
3. Determina si este dígito es mayor o igual a 5. Si es así, agregue 1 al dígito en el valor posicional dado. Si no, no cambie el dígito en el valor posicional dado.
4. Reemplazar todos los dígitos a la derecha del valor posicional dado por ceros.

1.2 - Agregar números enteros

• Notación de Adición: Para describir la suma, podemos usar símbolos y palabras.

Operación	Notación	Expresión	Leer como	Resultado
Adición	+	3 + 4	tres más cuatro	la suma de 3 y 4

Identidad Propiedad de Adición: La suma de cualquier número a y 0 es el número. $$\ begin {split} a + 0 &= a\\ 0 + a &= a\ end {split} $$
Propiedad Conmutativa de Adición: Cambiar el orden de las adiciones a y b no cambia su suma. $$a + b = b + a\ ldotp$$
Sumar números enteros.

Escribe los números para que cada valor posicional se alinee verticalmente.
Suma los dígitos en cada valor positorio. Trabajar de derecha a izquierda comenzando por el lugar de unos. Si una suma en un valor posicional es superior a 9, lleve al siguiente valor posicional.
Continuar agregando cada valor posicional de derecha a izquierda, agregando cada valor posicional y llevando si es necesario.

1.3 - Restar números enteros

Operación	Notación	Expresión	Leer como	Resultado
Resta	-	7 - 3	siete menos tres	la diferencia de 7 y 3

Restar números enteros.

Escribe los números para que cada valor posicional se alinee verticalmente.
Restar los dígitos en cada valor posicionar. Trabajar de derecha a izquierda comenzando por el lugar de unos. Si el dígito en la parte superior es menor que el dígito de abajo, tome prestado según sea necesario
Continuar restando cada valor posicional de derecha a izquierda, tomando prestado si es necesario.
Verifique agregando.

1.4 - Multiplicar números enteros

Operación	Notación	Expresión	Leer como	Resultado
Multiplicación	×	3 × 8	tres por ocho	el producto de 3 y 8
	•	3 • 8
	()	3 (8)

Propiedad de Multiplicación de Cero: El producto de cualquier número y 0 es 0. $$\ begin {split} a\ cdot 0 &= 0\\ 0\ cdot a &= 0\ end {split} $$
Identidad Propiedad de Multiplicación: El producto de cualquier número y 1 es el número. $$\ begin {split} 1\ cdot a &= a\\ a\ cdot 1 &= a\ end {split} $$
Propiedad conmutativa de la multiplicación: Cambiar el orden de los factores no cambia su producto. $$a\ cdot b = b\ cdot a\ ldotp$$
Multiplica dos números enteros para encontrar el producto.

Escribe los números para que cada valor posicional se alinee verticalmente.
Multiplique los dígitos en cada valor positorio.
Trabajar de derecha a izquierda, comenzando por los que se colocan en el número inferior.
Multiplique el número inferior por el dígito unos en el número superior, luego por el dígito de las decenas, y así sucesivamente.
Si un producto en un valor posicional es superior a 9, lleve al siguiente valor posicional.
Escribe los productos parciales, alineando los dígitos en los valores posicionales con los números anteriores. Repita para el lugar de las decenas en el número inferior, el lugar de los cientos, y así sucesivamente.
Inserte un cero como marcador de posición con cada producto parcial adicional.
Agregar los productos parciales.

1.5 - Dividir números enteros

Operación	Notación	Expresión	Leer como	Resultado
División	÷	12 ÷ 4	Doce dividido por cuatro	el cociente de 12 y 4
	$\dfrac{a}{b}$	$\dfrac{12}{4}$
	$b \overline{) a}$	$4 \overline{\smash{)}12}$
	a/b	12/4

Propiedades de División de Uno:
- Cualquier número (excepto 0) dividido por sí mismo es uno. $$a\ div a = 1$$
- Cualquier número dividido por uno es el mismo número. $$a\ div 1 = a$$
Propiedades de División de Cero:
- El cero dividido por cualquier número es 0. $$0\ div a = 0 $$
- Dividir un número por cero no está definido. $$a\ div 0 = indefinido$$
Dividir números enteros.

Dividir el primer dígito del dividendo por el divisor. Si el divisor es mayor que el primer dígito del dividendo, divida los dos primeros dígitos del dividendo por el divisor, y así sucesivamente.
Escribe el cociente por encima del dividendo.
Multiplique el cociente por el divisor y escriba el producto bajo el dividendo.
Restar ese producto del dividendo.
Bajar el siguiente dígito del dividendo.
Repita desde el Paso 1 hasta que no haya más dígitos en el dividendo para derribar.
Verifique multiplicando el cociente por el divisor.