4.2: Visualizar fracciones (Parte 2)

Última actualización
Guardar como PDF

Page ID: 114257

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Fracciones Equivalentes Modelo

Pensemos de nuevo en Andy y Bobby y su comida favorita. Si Andy come$\dfrac{1}{2}$ de una pizza y Bobby come$\dfrac{2}{4}$ de la pizza, ¿han comido la misma cantidad de pizza? En otras palabras, ¿no$\dfrac{1}{2} = \dfrac{2}{4}$? Podemos usar fichas de fracción para averiguar si Andy y Bobby han comido partes equivalentes de la pizza.

Definición: Fracciones Equivalentes

Las fracciones equivalentes son fracciones que tienen el mismo valor.

Las baldosas de fracción sirven como modelo útil de fracciones equivalentes. Es posible que desee utilizar fichas de fracción para realizar la siguiente actividad. O podrías hacer una copia de la Figura 4.3 y extenderla para incluir octavos, décimos y doceavos.

Comience con un$\dfrac{1}{2}$ azulejo. ¿Cuántas cuartas partes son la mitad? ¿Cuántas de las$\dfrac{1}{4}$ baldosas cubren exactamente la$\dfrac{1}{2}$ baldosa?

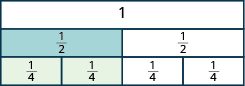
$Se muestra un rectángulo largo indiviso. Debajo hay un rectángulo dividido verticalmente en dos piezas, cada una etiquetada como una mitad. Debajo de eso hay un rectángulo dividido verticalmente en cuatro piezas, cada una etiquetada como una cuarta.$

Figura$\PageIndex{7}$

Ya que dos$\dfrac{1}{4}$ baldosas cubren la$\dfrac{1}{2}$ baldosa, vemos que$\dfrac{2}{4}$ es lo mismo que$\dfrac{1}{2}$, o$\dfrac{2}{4} = \dfrac{1}{2}$.

¿Cuántas de las$\dfrac{1}{6}$ baldosas cubren la$\dfrac{1}{2}$ baldosa?

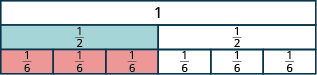
$Se muestra un rectángulo largo indiviso. Debajo hay un rectángulo dividido verticalmente en dos piezas, cada una etiquetada como una mitad. Debajo de eso hay un rectángulo dividido verticalmente en seis piezas, cada una etiquetada como una sexta parte.$

Figura$\PageIndex{8}$

Ya que tres$\dfrac{1}{6}$ baldosas cubren la$\dfrac{1}{2}$ baldosa, vemos que$\dfrac{3}{6}$ es lo mismo que$\dfrac{1}{2}$. Entonces,$\dfrac{3}{6} = \dfrac{1}{2}$. Las fracciones son fracciones equivalentes.

Ejemplo$\PageIndex{13}$: equivalent fractions

Usa fichas de fracciones para encontrar fracciones equivalentes. Muestra tu resultado con una figura.

¿Cuántos octavos son la mitad?
¿Cuántas décimas son la mitad?
¿Cuantos doceravos es igual a la mitad?

Solución

Se necesitan cuatro$\dfrac{1}{8}$ baldosas para cubrir exactamente la$\dfrac{1}{2}$ baldosa, entonces$\dfrac{4}{8} = \dfrac{1}{2}$.

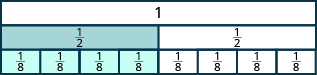
$Se muestra un rectángulo largo indiviso, etiquetado como 1. Debajo hay un rectángulo idéntico dividido verticalmente en dos piezas, cada una etiquetada 1 mitad. Debajo de eso hay un rectángulo idéntico dividido verticalmente en ocho piezas, cada una etiquetada 1 octava.$

Se necesitan cinco$\dfrac{1}{10}$ fichas para cubrir exactamente la$\dfrac{1}{2}$ baldosa, entonces$\dfrac{5}{10} = \dfrac{1}{2}$.

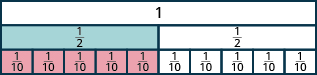
$Se muestra un rectángulo largo indiviso. Debajo hay un rectángulo dividido verticalmente en dos piezas, cada una etiquetada como una mitad. Debajo de eso hay un rectángulo dividido verticalmente en diez piezas, cada una etiquetada como una décima parte.$

Se necesitan seis$\dfrac{1}{12}$ baldosas para cubrir exactamente la$\dfrac{1}{2}$ baldosa, entonces$\dfrac{6}{12} = \dfrac{1}{2}$.

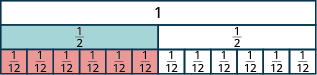
$Se muestra un rectángulo largo indiviso. Debajo hay un rectángulo dividido verticalmente en dos piezas, cada una etiquetada como una mitad. Debajo de eso hay un rectángulo dividido verticalmente en doce piezas, cada una etiquetada como una doceava.$

Supongamos que tenía mosaicos marcados$\dfrac{1}{20}$. ¿Cuántos de ellos se necesitaría para igualar$\dfrac{1}{2}$? ¿Estás pensando en diez fichas? Si lo eres, tienes razón, porque$\dfrac{10}{20} = \dfrac{1}{2}$.

Eso lo hemos demostrado$\dfrac{1}{2}, \dfrac{2}{4}, \dfrac{3}{6}, \dfrac{4}{8}, \dfrac{5}{10}, \dfrac{6}{12}$, y$\dfrac{10}{20}$ son todas fracciones equivalentes.

Ejercicio$\PageIndex{25}$

Usa fichas de fracciones para encontrar fracciones equivalentes: ¿Cuántos octavos equivalen a un cuarto?

Contestar: $2$

Ejercicio$\PageIndex{26}$

Usa fichas de fracciones para encontrar fracciones equivalentes: ¿Cuántas doceavos equivalen a una cuarta parte?

Contestar: $3$

Buscar Fracciones Equivalentes

Utilizamos fichas de fracción para mostrar que hay muchas fracciones equivalentes a$\dfrac{1}{2}$. Por ejemplo,$\dfrac{2}{4}, \dfrac{3}{6}$, y$\dfrac{4}{8}$ son todos equivalentes a$\dfrac{1}{2}$. Cuando alineamos las baldosas de fracción, se necesitaron cuatro de las$\dfrac{1}{8}$ baldosas para hacer la misma longitud que una$\dfrac{1}{2}$ baldosa. Esto demostró que$\dfrac{4}{8} = \dfrac{1}{2}$. Ver Ejemplo$\PageIndex{13}$.

Podemos mostrar esto con pizzas, también. La figura$\PageIndex{9a}$ muestra una sola pizza, cortada en dos trozos iguales con$\dfrac{1}{2}$ sombreado. En la figura se$\PageIndex{9b}$ muestra una segunda pizza del mismo tamaño, cortada en ocho trozos con$\dfrac{4}{8}$ sombra.

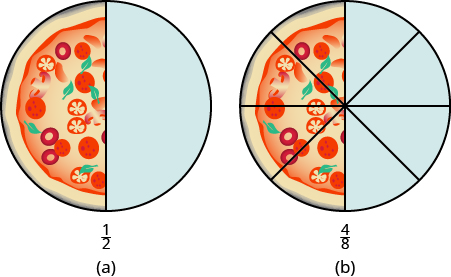
$Se muestran dos pizzas. La pizza de la izquierda se divide en 2 piezas iguales. 1 pieza está sombreada. La pizza de la derecha se divide en 8 piezas iguales. 4 piezas están sombreadas.$

Figura$\PageIndex{9}$

Esta es otra forma de demostrar que$\dfrac{1}{2}$ es equivalente a$\dfrac{4}{8}$. ¿Cómo podemos usar las matemáticas para$\dfrac{1}{2}$ cambiarnos$frac{4}{8}$? ¿Cómo podrías tomar una pizza que se corta en dos trozos y cortarla en ocho trozos? ¡Podrías cortar cada una de las dos piezas más grandes en cuatro piezas más pequeñas! La pizza entera se cortaría entonces en ocho trozos en lugar de sólo dos. Matemáticamente, lo que hemos descrito podría escribirse como:

\[\dfrac{1 \cdot \textcolor{blue}{4}}{2 \cdot \textcolor{blue}{4}} = \dfrac{4}{8} \nonumber \]

Estos modelos llevan a la Propiedad de Fracciones Equivalentes, que establece que si multiplicamos el numerador y denominador de una fracción por el mismo número, el valor de la fracción no cambia.

Definición: Propiedad de Fracciones Equivalentes

Si$a$,$b$, y$c$ son números donde$b ≠ 0$ y$c ≠ 0$, entonces

\[\dfrac{a}{b} = \dfrac{a \cdot c}{b \cdot c}\]

Cuando se trabaja con fracciones, a menudo es necesario expresar la misma fracción en diferentes formas. Para encontrar formas equivalentes de una fracción, podemos usar la Propiedad de Fracciones Equivalentes. Por ejemplo, considere la fracción la mitad.

\[\begin{split} \dfrac{1 \cdot \textcolor{blue}{3}}{2 \cdot \textcolor{blue}{3}} = \dfrac{3}{6} \; & so \; \dfrac{1}{2} = \dfrac{3}{6} \\ \dfrac{1 \cdot \textcolor{blue}{2}}{2 \cdot \textcolor{blue}{2}} = \dfrac{2}{4} \; & so \; \dfrac{1}{2} = \dfrac{2}{4} \\ \dfrac{1 \cdot \textcolor{blue}{10}}{2 \cdot \textcolor{blue}{10}} = \dfrac{10}{20} \; & so \; \dfrac{1}{2} = \dfrac{10}{20} \end{split} \nonumber \]

Entonces, decimos eso$\dfrac{1}{2}, \dfrac{2}{4}, \dfrac{3}{6}$, y$\dfrac{10}{20}$ son fracciones equivalentes.

Ejemplo$\PageIndex{14}$: equivalent fractions

Encuentra tres fracciones equivalentes a$\dfrac{2}{5}$.

Solución

Para encontrar una fracción equivalente a$\dfrac{2}{5}$, multiplicamos el numerador y denominador por el mismo número (pero no por cero). Multipliquémoslos por$2$,$3$, y$5$.

\[\dfrac{2 \cdot \textcolor{blue}{2}}{5 \cdot \textcolor{blue}{2}} = \dfrac{4}{10} \qquad \dfrac{2 \cdot \textcolor{blue}{3}}{5 \cdot \textcolor{blue}{3}} = \dfrac{6}{15} \qquad \dfrac{2 \cdot \textcolor{blue}{5}}{5 \cdot \textcolor{blue}{5}} = \dfrac{10}{25} \nonumber \]

Entonces,$\dfrac{4}{10}, \dfrac{6}{15}$, y$\dfrac{10}{25}$ son equivalentes a$\dfrac{2}{5}$.

Ejercicio$\PageIndex{27}$

Encuentra tres fracciones equivalentes a$\dfrac{3}{5}$.

Contestar: Las respuestas correctas incluyen$\dfrac{6}{10}, \dfrac{9}{15}$ y$\dfrac{12}{20}$

Ejercicio$\PageIndex{28}$

Encuentra tres fracciones equivalentes a$\dfrac{4}{5}$.

Contestar: Las respuestas correctas incluyen$\dfrac{8}{10}, \dfrac{12}{15}$ y$\dfrac{16}{20}$

Ejemplo$\PageIndex{15}$: equivalent fractions

Encuentra una fracción con un denominador de 21 que sea equivalente a$\dfrac{2}{7}$.

Solución

Para encontrar fracciones equivalentes, multiplicamos el numerador y el denominador por el mismo número. En este caso, necesitamos multiplicar el denominador por un número que resulte en$21$.

Ya que podemos$3$ multiplicar$7$ por para obtener$21$, podemos encontrar la fracción equivalente multiplicando tanto el numerador como el denominador por$3$.

\[\dfrac{2}{7} = \dfrac{2 \cdot \textcolor{blue}{3}}{7 \cdot \textcolor{blue}{3}} = \dfrac{6}{21} \nonumber \]

Ejercicio$\PageIndex{29}$

Encontrar una fracción con un denominador de$21$ que sea equivalente a$\dfrac{6}{7}$.

Contestar: $\dfrac{18}{21}$

Ejercicio$\PageIndex{30}$

Encontrar una fracción con un denominador de$100$ que sea equivalente a$\dfrac{3}{10}$.

Contestar: $\dfrac{30}{100}$

Localizar fracciones y números mixtos en la línea numérica

Ahora estamos listos para trazar fracciones en una recta numérica. Esto nos ayudará a visualizar fracciones y comprender sus valores.

Localicemos$\dfrac{1}{5}, \dfrac{4}{5}, 3, 3 \dfrac{1}{3}, \dfrac{7}{4}, \dfrac{9}{2}, 5$, y$\dfrac{8}{3}$ en la línea numérica. Empezaremos con los números enteros$3$ y$5$ porque son los más fáciles de trazar.

$Se muestra una línea numérica con los números 3, 4 y 5. Hay puntos rojos a las 3 y a las 5.$

Las fracciones propias listadas son$\dfrac{1}{5}$ y$\dfrac{4}{5}$. Sabemos que las fracciones propiamente dichas tienen valores menores a uno, por lo que$\dfrac{1}{5}$ y$\dfrac{1}{5}$ se ubican entre los números enteros$0$ y$1$. Los denominadores son ambos$5$, por lo que necesitamos dividir el segmento de la recta numérica entre$0$ y$1$ en cinco partes iguales. Podemos hacer esto dibujando cuatro marcas igualmente espaciadas en la recta numérica, que luego podemos etiquetar como$\dfrac{1}{5}, \dfrac{2}{5}, \dfrac{3}{5}$, y$\dfrac{4}{5}$. Ahora trazar puntos en$\dfrac{1}{5}$ y$\dfrac{4}{5}$.

$Se muestra una línea numérica. Muestra 0, 1 quinto, 2 quintos, 3 quintos, 4 quintos y 1. Hay puntos rojos a la 1 quinta y a las 4 quintas partes.$

El único número mixto para trazar es$3 \dfrac{1}{3}$. ¿Entre qué hay dos números enteros$3 \dfrac{1}{3}$? Recuerda que un número mixto es un número entero más una fracción propia, entonces$3 \dfrac{1}{3} > 3$. Ya que es mayor que$3$, pero no una unidad entera mayor,$3 \dfrac{1}{3}$ es entre$3$ y$4$. Necesitamos dividir la porción de la línea numérica entre$3$ y$4$ en tres partes iguales (tercios) y trazar$3 \dfrac{1}{3}$ en la primera marca.

$Se muestra una línea numérica con el número entero del 0 al 5. Entre 3 y 4, se etiquetan 3 y 1 tercio y 3 y 2 tercios. Hay un punto rojo en 3 y 1 tercio.$

Por último, mira las fracciones impropias$\dfrac{7}{4}, \dfrac{9}{2}$, y$\dfrac{8}{3}$. Ubicar estos puntos será más fácil si cambias cada uno de ellos a un número mixto.

\[\dfrac{7}{4} = 1 \dfrac{3}{4}, \qquad \dfrac{9}{2} = 4 \dfrac{1}{2}, \qquad \dfrac{8}{3} = 2 \dfrac{2}{3} \nonumber \]

Aquí está la recta numérica con todos los puntos trazados.

$Se muestra una línea numérica con números enteros del 0 al 6. Entre 0 y 1, se etiquetan 1 quinto y 4 quintos y se muestran con puntos rojos. Entre 1 y 2, 7 cuartos se etiquetan y se muestran con un punto rojo. Entre 2 y 3, 8 tercios se etiquetan y se muestran con un punto rojo. Entre 3 y 4, 3 y 1 tercio se etiqueta y se muestra con un punto rojo. Entre 4 y 5, 9 mitades se etiquetan y se muestran con un punto rojo.$

Ejemplo$\PageIndex{16}$: locate and label

Localice y etiquete lo siguiente en una línea numérica:$\dfrac{3}{4}, \dfrac{4}{3}, \dfrac{5}{3}, 4 \dfrac{1}{5}$, y$\dfrac{7}{2}$.

Solución

Comience por localizar la fracción adecuada$\dfrac{3}{4}$. Es entre$0$ y$1$. Para ello, divida la distancia entre$0$ y$1$ en cuatro partes iguales. Después, trazar$\dfrac{3}{4}$.

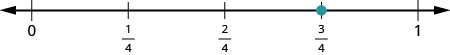
$Se muestra una línea numérica. Muestra 0, 1 cuarto, 2 cuartos, 3 cuartos y 1. Hay un punto rojo a las 3 cuartas partes.$

A continuación, localice el número mixto$4 \dfrac{1}{5}$. Está entre$4$ y$5$ en la recta numérica. Divida la línea numérica entre$4$ y$5$ en cinco partes iguales, y luego trazar$4 \dfrac{1}{5}$ una quinta parte del camino entre$4$ y$5$.

$Se muestra una línea numérica. Muestra 4, 4 y 1 quinto, 4 y 2 quintos, 4 y 3 quintos, 4 y 4 quintos, y 5. Hay un punto rojo en 4 y 1 quinto.$

Ahora localice las fracciones impropias$\dfrac{4}{3}$ y$\dfrac{5}{3}$. Es más fácil trazarlos si primero los convertimos a números mixtos.

\[\dfrac{4}{3} = 1 \dfrac{1}{3}, \qquad \dfrac{5}{3} = 1 \dfrac{2}{3} \nonumber\]

Divide la distancia entre$1$ y$2$ en tercios.

$Se muestra una línea numérica. Muestra 1, 1 y 1 tercio, 1 y 2 tercios, y 2. Debajo de 1 dice 3 tercios. Por debajo de 1 y 1 tercio dice 4 tercios. Por debajo de 1 y 2 tercios dice 5 tercios. Debajo de 2 dice 6 tercios. Hay puntos rojos en 1 y 1 tercio y 1 y 2 tercios.$

A continuación vamos a trazar$\dfrac{7}{2}$. Lo escribimos como un número mixto,$\dfrac{7}{2} = 3 \dfrac{1}{2}$. Trazarlo entre$3$ y$4$.

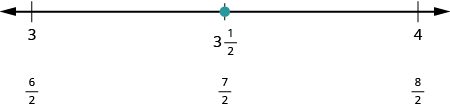
$Se muestra una línea numérica. Se muestran 3, 3 y 1 mitad, y 4. Debajo de 3 dice 6 mitades. Por debajo de 3 y 1 mitad dice 7 mitades. Debajo de 4 dice 8 mitades. Hay un punto rojo a las 3 y 1 mitad.$

La línea numérica muestra todos los números ubicados en la recta numérica.

$Se muestra una línea numérica. Muestra los números enteros del 0 al 5. Entre 2 números cualesquiera hay 10 marcas de verificación. Entre 0 y 1, entre la 7ª y la 8ª marca de verificación, se etiquetan 3 cuartos y se muestran con un punto rojo. Entre 1 y 2, 4 tercios y 5 tercios se etiquetan y se muestran con puntos rojos. Entre 3 y 4, se etiquetan 7 mitades y se muestran con un punto rojo. Entre 4 y 5, 4 y 1 quinto se etiqueta y se muestra con un punto rojo.$

Ejercicio$\PageIndex{31}$

Localice y etiquete lo siguiente en una recta numérica:$\dfrac{1}{3}, \dfrac{5}{4}, \dfrac{7}{4}, 2 \dfrac{3}{5}, \dfrac{9}{2}$.

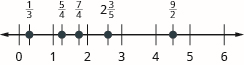
Contestar: $Ejercicio 4.1.31.png$

Ejercicio$\PageIndex{32}$

Localice y etiquete lo siguiente en una recta numérica:$\dfrac{2}{3}, \dfrac{5}{2}, \dfrac{9}{4}, \dfrac{11}{4}, 3 \dfrac{2}{5}$.

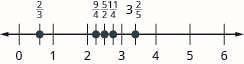
Contestar: $Ejercicio 4.1.32.png$

En Introducción a los enteros, definimos lo contrario de un número. Es el número que está a la misma distancia de cero en la recta numérica pero en el lado opuesto de cero. Vimos, por ejemplo, que lo contrario de$7$ es$−7$ y lo contrario de$−$ 7 es$7$.

$Se muestra una línea numérica. Se muestran los números negativos 7, 0 y 7. Hay puntos rojos en negativo 7 y 7. El espacio entre 7 y 0 negativo se etiqueta como 7 unidades. El espacio entre 0 y 7 está etiquetado como 7 unidades.$

Las fracciones también tienen opuestos. Lo contrario de$\dfrac{3}{4}$ es$− \dfrac{3}{4}$. Es la misma distancia de$0$ en la recta numérica, pero en el lado opuesto de$0$.

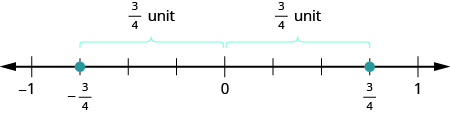
$Se muestra una línea numérica. Muestra los números negativos 1, negativos 3 cuartos, 0, 3 cuartos y 1. Hay puntos rojos en 3 cuartos y 3 cuartos negativos. El espacio entre 3 cuartos y 0 negativos se etiqueta como 3 cuartos de una unidad. El espacio entre 0 y 3 cuartos está etiquetado como 3 cuartos de una unidad.$

Pensar en las fracciones negativas como lo contrario de las fracciones positivas nos ayudará a ubicarlas en la recta numérica. Para ubicar$− \dfrac{15}{8}$ en la recta numérica, primero piense en dónde$\dfrac{15}{8}$ se encuentra. Es una fracción impropia, por lo que primero la convertimos al número mixto$1 \dfrac{7}{8}$ y vemos que estará entre$1$ y$2$ en la recta numérica. Entonces su opuesto,$− \dfrac{15}{8}$, será entre$−1$ y$−2$ en la recta numérica.

$Se muestra una línea numérica. Muestra los números negativos 2, negativos 1, 0, 1 y 2. Entre negativo 2 y negativo 1, negativo 1 y 7 octavos está etiquetado y marcado con un punto rojo. La distancia entre negativo 1 y 7 octavos y 0 se marca como 15 octavos unidades. Entre 1 y 2, 1 y 7 octavos está etiquetado y marcado con un punto rojo. La distancia entre 0 y 1 y 7 octavos se marca como 15 octavos unidades.$

Ejemplo$\PageIndex{17}$: locate and label

Localice y etiquete lo siguiente en la línea numérica:$\dfrac{1}{4}, − \dfrac{1}{4}, 1 \dfrac{1}{3}, −1 \dfrac{1}{3}, \dfrac{5}{2}$, y$− \dfrac{5}{2}$.

Solución

Dibuja una recta numérica. Marcar$0$ en el medio y luego marcar varias unidades a izquierda y derecha.

Para ubicar$\dfrac{1}{4}$, divida el intervalo entre$0$ y$1$ en cuatro partes iguales. Cada parte representa un cuarto de la distancia. Así que trama$\dfrac{1}{4}$ a la primera marca.

$Se muestra una línea numérica. Se muestran los números negativos 4, negativo 3, negativo 2, negativo 1, 0, 1, 2, 3 y 4. Hay 4 marcas de verificación entre el 1 y el 0 negativo. Hay 4 marcas de verificación entre 0 y 1. La primera marca entre 0 y 1 está etiquetada como 1 cuarta y marcada con un punto rojo.$

Para ubicar$− \dfrac{1}{4}$, divida el intervalo entre$0$ y$−1$ en cuatro partes iguales. Parcela$− \dfrac{1}{4}$ en la primera marca a la izquierda de$0$.

Dado que$1 \dfrac{1}{3}$ es entre$1$ y$2$, dividir el intervalo entre$1$ y$2$ en tres partes iguales. Trazar$1 \dfrac{1}{3}$ a la primera marca a la derecha de$1$. Entonces ya que$−1 \dfrac{1}{3}$ es lo contrario de$1 \dfrac{1}{3}$ que es entre$−1$ y$−2$. Divida el intervalo entre$−1$ y$−2$ en tres partes iguales. Parcela$−1 \dfrac{1}{3}$ en la primera marca a la izquierda de$−1$.

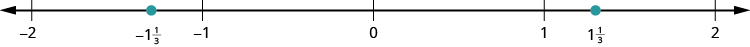
$Se muestra una línea numérica. Se etiquetan los números enteros de 2 a 2 negativos. Entre negativo 2 y negativo 1, negativo 1 y 1 tercio se etiqueta y se marca con un punto rojo. Entre 1 y 2, 1 y 1 tercio está etiquetado y marcado con un punto rojo.$

Para ubicar$\dfrac{5}{2}$ y$− \dfrac{5}{2}$, puede ser útil reescribirlos como los números mixtos$2 \dfrac{1}{2}$ y$−2 \dfrac{1}{2}$. Dado que$2 \dfrac{1}{2}$ es entre$2$ y$3$, dividir el intervalo entre$2$ y$3$ en dos partes iguales. Trama$\dfrac{5}{2}$ en la marca. Entonces ya que$−2 \dfrac{1}{2}$ es entre$−2$ y$−3$, dividir el intervalo entre$−2$ y$−3$ en dos partes iguales. Trama$− \dfrac{5}{2}$ en la marca.

$Se muestra una línea numérica. Se etiquetan los números enteros de 4 a 4 negativos. Entre negativo 3 y negativo 2, se etiquetan 5 mitades negativas y se marcan con un punto rojo. Entre 2 y 3, 5 mitades está etiquetada y marcada con un punto rojo.$

Ejercicio$\PageIndex{33}$

Localice y etiquete cada una de las fracciones dadas en una recta numérica:$\dfrac{2}{3}, − \dfrac{2}{3}, 2 \dfrac{1}{4}, −2 \dfrac{1}{4}, \dfrac{3}{2}, − \dfrac{3}{2}$

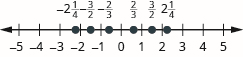
Contestar: $Ejercicio 4.1.33.png$

Ejercicio$\PageIndex{34}$

Localice y etiquete cada una de las fracciones dadas en una recta numérica:$\dfrac{3}{4}, − \dfrac{3}{4}, 1 \dfrac{1}{2}, −1 \dfrac{1}{2}, \dfrac{7}{3}, − \dfrac{7}{3}$

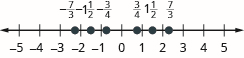
Contestar: $Ejercicio 4.1.34.png$

Fracciones de orden y números mixtos

Podemos usar los símbolos de desigualdad para ordenar fracciones. Recuerda que$a > b$ significa que$a$ está a la derecha de$b$ en la recta numérica. A medida que nos movemos de izquierda a derecha en una recta numérica, los valores aumentan.

Ejemplo$\PageIndex{18}$: order

Ordene cada uno de los siguientes pares de números, usando$<$ o$>$:

$− \dfrac{2}{3}$____$−1$
$−3 \dfrac{1}{2}$____$−3$
$− \dfrac{3}{7}$____$− \dfrac{3}{8}$
$−2$____$− \dfrac{16}{9}$

Solución

$− \dfrac{2}{3} > −1$

$Se muestra una línea numérica. Se etiquetan los números enteros de 3 a 3 negativos. El negativo 1 está marcado con un punto rojo. Entre los negativos 1 y 0, se etiquetan 2 tercios negativos y se marcan con un punto rojo.$

$−3 \dfrac{1}{2} < −3$

$Se muestra una línea numérica. Se etiquetan los números enteros de 4 a 4 negativos. Hay un punto rojo en negativo 3. Entre negativo 4 y negativo 3, negativo 3 y medio se etiqueta y se marca con un punto rojo.$

$− \dfrac{3}{7} < − \dfrac{3}{8}$

$Se muestra una línea numérica. Los números negativos 3, negativos 2, negativos 1, 0, 1, 2 y 3 están etiquetados. Entre los negativos 1 y 0, los 3 séptimos negativos y los 3 octavos negativos se etiquetan y se marcan con puntos rojos.$

$−2 < − \dfrac{16}{9}$

$Se muestra una línea numérica. Los números negativos 3, negativos 2, negativos 1, 0, 1, 2 y 3 están etiquetados. Hay un punto rojo en negativo 2. Entre negativo 2 y negativo 1, negativo 16 sobre 9 se etiqueta y se marca con un punto rojo.$

Ejercicio$\PageIndex{35}$

Ordene cada uno de los siguientes pares de números, usando$<$ o$>$:

$− \dfrac{1}{3}$__$−1$
$−1 \dfrac{1}{2}$__$− 2$
$− \dfrac{2}{3}$__$− \dfrac{1}{3}$
$−3$__$− \dfrac{7}{3}$

Contestar a: $>$
Respuesta b: $>$
Respuesta c: $<$
Respuesta d: $<$

Ejercicio$\PageIndex{36}$

Ordene cada uno de los siguientes pares de números, usando$<$ o$>$:

$−3$__$− \dfrac{17}{5}$
$−2 \dfrac{1}{4}$__$−2$
$− \dfrac{3}{5}$__$− \dfrac{4}{5}$
$−4$__$− \dfrac{10}{3}$

Contestar a: $>$
Respuesta b: $<$
Respuesta c: $>$
Respuesta d: $<$

Acceda a recursos adicionales en línea

Introducción a las Fracciones
Identificar fracciones usando bloques de patrón

Conceptos clave

Propiedad de One
- Cualquier número, excepto cero, dividido por sí mismo es uno.
  $\dfrac{a}{a}=1$, donde$a\neq 0$.
Números Mixtos
- Un número mixto consiste en un número entero$a$ y una fracción$\dfrac{b}{c}$ donde$c \neq 0$.
- Está escrito de la siguiente manera:$a\dfrac{b}{c}$$c \neq 0$
Fracciones propias e impropias
- La fracción$\frac{a}{b}$ es una fracción propia si$a<b$ y una fracción impropia si$a \geq b$.
Convertir una fracción impropia en un número mixto.
1. Divide el denominador en el numerador.
2. Identificar el cociente, el resto y el divisor.
3. Escribe el número mixto como$\dfrac{\text{remainder}}{\text{divisor}}$.
Convierte un número mixto en una fracción impropia.
1. Multiplica el número entero por el denominador.
2. Agrega el numerador al producto que se encuentra en el Paso 1.
3. Escribe la suma final sobre el denominador original.
Propiedad Fracciones Equivalentes
- Si$a$,$b$ y$c$ son números donde$b \neq 0$$c \neq 0$, entonces\ (\ dfrac {a} {b} =\ dfrac {a\ cdot c} {b\ cdot c}\]).

Glosario

fracciones equivalentes: Las fracciones equivalentes son dos o más fracciones que tienen el mismo valor.
fracción: Se escribe una fracción$\dfrac{a}{b}$. en una fracción,$a$ es el numerador y$b$ es el denominador. Una fracción representa partes de un todo. El denominador$b$ es el número de partes iguales en las que se ha dividido el conjunto, y el numerador$a$ indica cuántas partes están incluidas.
número mixto: Un número mixto consiste en un número entero$a$ y una fracción$\dfrac{b}{c}$ donde$c \neq 0$. Está escrito como$a\dfrac{b}{c}$, dónde$c \neq 0$.
fracciones propias e impropias: La fracción$\dfrac{a}{b}$ es propia si$a<b$ e impropia si$a>b$.

La práctica hace la perfección

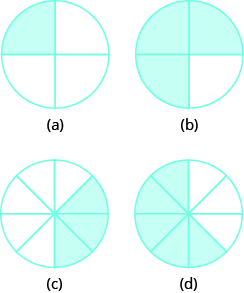
$En la parte “a”, un círculo se divide en 4 piezas iguales. 1 pieza está sombreada. En la parte “b”, un círculo se divide en 4 piezas iguales. 3 piezas están sombreadas. En la parte “c”, un círculo se divide en 8 piezas iguales. 3 piezas están sombreadas. En la parte “d”, un círculo se divide en 8 piezas iguales. 5 piezas están sombreadas.$
$En la parte “a”, un círculo se divide en 12 piezas iguales. 7 piezas están sombreadas. En la parte “b”, un círculo se divide en 12 piezas iguales. 5 piezas están sombreadas. En la parte “c”, un cuadrado se divide en 9 piezas iguales. 4 de las piezas están sombreadas. En la parte “d”, un cuadrado se divide en 9 piezas iguales. 5 piezas están sombreadas.$

En los siguientes ejercicios, sombrea partes de círculos o cuadrados para modelar las siguientes fracciones.

$\dfrac{1}{2}$
$\dfrac{1}{3}$
$\dfrac{3}{4}$
$\dfrac{2}{5}$
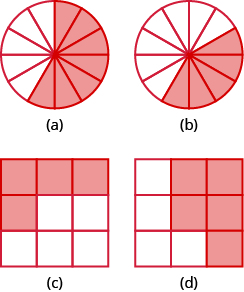
$\dfrac{5}{6}$
$\dfrac{7}{8}$
$\dfrac{5}{8}$
$\dfrac{7}{10}$

En los siguientes ejercicios, usa círculos de fracción para hacer enteros, si es posible, con las siguientes piezas.

3 tercios
8 octavos
7 sextos
4 tercios
7 quintas
7 cuartas partes

En los siguientes ejercicios, nombra las fracciones impropias. Después escribe cada fracción impropia como un número mixto.

$En la parte “a”, se muestran dos círculos. Cada uno se divide en 4 piezas iguales. El círculo de la izquierda tiene las 4 piezas sombreadas. El círculo de la derecha tiene 1 pieza sombreada. En la parte “b”, se muestran dos círculos. Cada uno se divide en 4 piezas iguales. El círculo de la izquierda tiene las 4 piezas sombreadas. El círculo de la derecha tiene 3 piezas sombreadas. En la parte “c”, se muestran dos círculos. Cada uno se divide en 8 piezas iguales. El círculo de la izquierda tiene las 8 piezas sombreadas. El círculo de la derecha tiene 3 piezas sombreadas.$
$En la parte “a”, se muestran 2 círculos. Cada uno se divide en 8 piezas iguales. El círculo de la izquierda tiene las 8 piezas sombreadas. El círculo de la derecha tiene 1 pieza sombreada. En la parte “b”, se muestran dos cuadrados. Cada uno se divide en 4 piezas iguales. El cuadrado de la izquierda tiene las 4 piezas sombreadas. El círculo de la derecha tiene 1 pieza sombreada. En la parte “c”, se muestran dos cuadrados. Cada uno se divide en 9 piezas iguales. El cuadrado de la izquierda tiene todas las 9 piezas sombreadas. El cuadrado de la derecha tiene 2 piezas sombreadas.$
$En la parte “a”, se muestran 3 círculos. Cada uno se divide en 4 piezas iguales. Los dos primeros círculos tienen las 4 piezas sombreadas. El tercer círculo tiene 3 piezas sombreadas. En la parte “b”, se muestran 3 círculos. Cada uno se divide en 8 piezas iguales. Los dos primeros círculos tienen las 8 piezas sombreadas. El tercer círculo tiene 3 piezas sombreadas.$

En los siguientes ejercicios, dibuja círculos de fracciones para modelar la fracción dada.

$\dfrac{3}{3}$
$\dfrac{4}{4}$
$\dfrac{7}{4}$
$\dfrac{5}{3}$
$\dfrac{11}{6}$
$\dfrac{13}{8}$
$\dfrac{10}{3}$
$\dfrac{9}{4}$

En los siguientes ejercicios, reescribe la fracción impropia como un número mixto.

$\dfrac{3}{2}$
$\dfrac{5}{3}$
$\dfrac{11}{4}$
$\dfrac{13}{5}$
$\dfrac{25}{6}$
$\dfrac{28}{9}$
$\dfrac{42}{13}$
$\dfrac{47}{15}$

En los siguientes ejercicios, reescribe el número mixto como una fracción impropia.

$1 \dfrac{2}{3}$
$1 \dfrac{2}{5}$
$2 \dfrac{1}{4}$
$2 \dfrac{5}{6}$
$2 \dfrac{7}{9}$
$2 \dfrac{5}{7}$
$3 \dfrac{4}{7}$
$3 \dfrac{5}{9}$

En los siguientes ejercicios, usa fichas de fracciones o dibuja una figura para encontrar fracciones equivalentes.

¿Cuántos sextos es igual a un tercio?
¿Cuántos doceavos es igual a un tercio?
¿Cuántos octavos es igual tres cuartas partes?
¿Cuántos doceavos es igual tres cuartas partes?
¿Cuántos cuartos es igual tres-mitades?
¿Cuántos sextos es igual tres-mitades?

En los siguientes ejercicios, encuentra tres fracciones equivalentes a la fracción dada. Muestra tu obra, usando figuras o álgebra.

$\dfrac{1}{4}$
$\dfrac{1}{3}$
$\dfrac{3}{8}$
$\dfrac{5}{6}$
$\dfrac{2}{7}$
$\dfrac{5}{9}$

En los siguientes ejercicios, trazar los números en una recta numérica.

$\dfrac{2}{3}, \dfrac{5}{4}, \dfrac{12}{5}$
$\dfrac{1}{3}, \dfrac{7}{4}, \dfrac{13}{5}$
$\dfrac{1}{4}, \dfrac{9}{5}, \dfrac{11}{3}$
$\dfrac{7}{10}, \dfrac{5}{2}, \dfrac{13}{8}, 3$
$2 \dfrac{1}{3}, −2 \dfrac{1}{3}$
$1 \dfrac{3}{4}, −1 \dfrac{3}{5}$
$\dfrac{3}{4}, − \dfrac{3}{4}, 1 \dfrac{2}{3}, −1 \dfrac{2}{3}, \dfrac{5}{2}, − \dfrac{5}{2}$
$\dfrac{2}{5}, − \dfrac{2}{5}, 1 \dfrac{3}{4}, −1 \dfrac{3}{4}, \dfrac{8}{3}, − \dfrac{8}{3}$

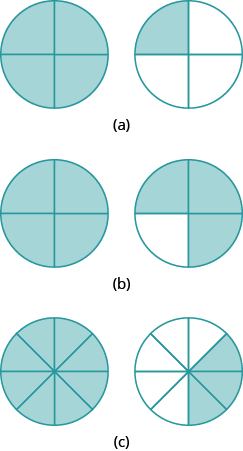
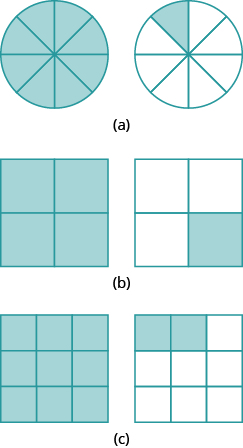
En los siguientes ejercicios, ordene cada uno de los siguientes pares de números, utilizando < or >.

−1__$− \dfrac{1}{4}$
−1__$− \dfrac{1}{3}$
$−2 \dfrac{1}{2}$__− 3
$−1 \dfrac{3}{4}$__− 2
$− \dfrac{5}{12}$__$− \dfrac{7}{12}$
$− \dfrac{9}{10}$__$− \dfrac{3}{10}$
−3__$− \dfrac{13}{5}$
−4__$− \dfrac{23}{6}$

Matemáticas cotidianas

Medidas musicales Un baile coreografiado se divide en recuentos. Un$\dfrac{1}{1}$ conteo tiene un paso en un conteo, un$\dfrac{1}{2}$ conteo tiene dos pasos en un conteo y un conteo de 1 3 tiene tres pasos en un conteo. ¿Cuántos pasos habría en un$\dfrac{1}{5}$ conteo? ¿Qué tipo de conteo tiene cuatro pasos en él?
Medidas musicales Las fracciones se utilizan a menudo en la música. En 4 4 tiempos, hay cuatro notas de cuarto en un compás.
1. ¿Cuántas medidas tomarían las notas de ocho cuartos?
2. La canción “Happy Birthday to You” tiene 25 notas de cuarto. ¿Cuántas medidas hay en “Feliz Cumpleaños a Ti?”
Hornear Nina está haciendo cinco sartenes de caramelo para servir después de un recital musical. Por cada sartén, necesita 1 2 taza de nueces.
1. ¿Cuántas tazas de nueces necesita para cinco sartenes de caramelo?
2. ¿Crees que es más fácil medir esta cantidad cuando usas una fracción impropia o un número mixto? ¿Por qué?

Ejercicios de escritura

Da un ejemplo de tu experiencia de vida (fuera de la escuela) donde era importante entender fracciones.
Explica cómo localizas la fracción impropia$\dfrac{21}{4}$ en una recta numérica en la que solo están marcados los números enteros del 0 al 10.

Autocomprobación

(a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

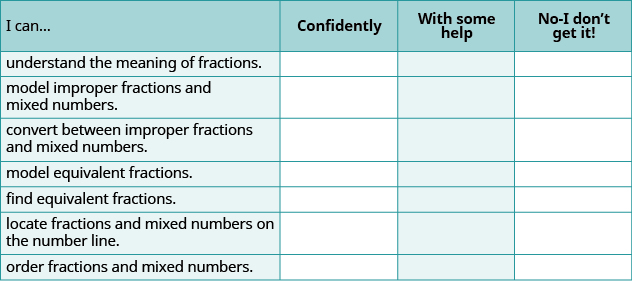
(b) Si la mayoría de sus cheques fueron:

... con confianza. ¡Felicidades! Has logrado los objetivos en esta sección. Reflexiona sobre las habilidades de estudio que usaste para que puedas seguir usándolas. ¿Qué hiciste para confiar en tu capacidad para hacer estas cosas? Ser específico.

... con alguna ayuda. Esto debe abordarse rápidamente porque los temas que no dominas se convierten en baches en tu camino hacia el éxito. En matemáticas, cada tema se basa en trabajos anteriores. Es importante asegurarse de tener una base sólida antes de seguir adelante. ¿A quién puedes pedir ayuda? Tus compañeros de clase e instructor son buenos recursos. ¿Hay algún lugar en el campus donde estén disponibles los tutores de matemáticas? ¿Se pueden mejorar tus habilidades de estudio?

... no, ¡no lo consigo! Esta es una señal de advertencia y no debes ignorarla. Debería obtener ayuda de inmediato o rápidamente se verá abrumado. Consulte a su instructor lo antes posible para discutir su situación. Juntos pueden idear un plan para obtener la ayuda que necesita.

Colaboradores y Atribuciones

Template:ContribOpenStaxPreAlgebra

Search

Text Color

Text Size

Margin Size

Font Type

Definición: Fracciones Equivalentes

Ejemplo\(\PageIndex{13}\): equivalent fractions

Ejercicio\(\PageIndex{25}\)

Ejercicio\(\PageIndex{26}\)

Definición: Propiedad de Fracciones Equivalentes

Ejemplo\(\PageIndex{14}\): equivalent fractions

Ejercicio\(\PageIndex{27}\)

Ejercicio\(\PageIndex{28}\)

Ejemplo\(\PageIndex{15}\): equivalent fractions

Ejercicio\(\PageIndex{29}\)

Ejercicio\(\PageIndex{30}\)

Ejemplo\(\PageIndex{16}\): locate and label

Ejercicio\(\PageIndex{31}\)

Ejercicio\(\PageIndex{32}\)

Ejemplo\(\PageIndex{17}\): locate and label

Ejercicio\(\PageIndex{33}\)

Ejercicio\(\PageIndex{34}\)

Ejemplo\(\PageIndex{18}\): order

Ejercicio\(\PageIndex{35}\)

Ejercicio\(\PageIndex{36}\)