4.1: Visualizar fracciones (Parte 1)
- Page ID
- 114241
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Comprender el significado de las fracciones
- Modele fracciones impropias y números mixtos
- Convertir entre fracciones impropias y números mixtos
- Modelar fracciones equivalentes
- Encuentra fracciones equivalentes
- Localizar fracciones y números mixtos en la recta numérica
- Ordenar fracciones y números mixtos
Antes de comenzar, toma este cuestionario de preparación.
- Simplificar:\(5 • 2 + 1\). Si te perdiste este problema, revisa el Ejemplo 2.1.8.
- Rellene el espacio en blanco con\(<\) o\(>\):\(−2\) __\(−5\). Si te perdiste este problema, revisa el Ejemplo 3.1.2.
Comprender el significado de las fracciones
A Andy y Bobby les encanta la pizza. El lunes por la noche, comparten una pizza por igual. ¿Cuánto de la pizza obtiene cada uno? ¿Estás pensando que cada chico recibe la mitad de la pizza? Así es. Hay una pizza entera, dividida uniformemente en dos partes, por lo que cada niño obtiene una de las dos partes iguales. En matemáticas, escribimos\(\dfrac{1}{2}\) para significar una de cada dos partes.
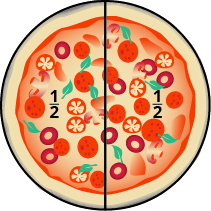
Figura\(\PageIndex{1}\)
El martes, Andy y Bobby comparten una pizza con sus padres, Fred y Christy, con cada persona recibiendo la misma cantidad de la pizza entera. ¿Cuánto de la pizza obtiene cada persona? Hay una pizza entera, dividida de manera uniforme en cuatro partes iguales. Cada persona tiene una de las cuatro partes iguales, así que cada una tiene\(\dfrac{1}{4}\) de la pizza.

Figura\(\PageIndex{2}\)
El miércoles, la familia invita a algunos amigos a una cena de pizza. Hay un total de\(12\) personas. Si comparten la pizza por igual, cada persona obtendría\(\dfrac{1}{12}\) de la pizza.
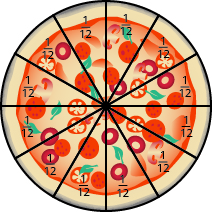
Figura\(\PageIndex{3}\)
Se escribe una fracción\(\dfrac{a}{b}\), donde\(a\) y\(b\) son enteros y\(b ≠ 0\). En una fracción,\(a\) se llama numerador y\(b\) se llama denominador.
Una fracción es una forma de representar partes de un todo. El denominador\(b\) representa el número de partes iguales en las que se ha dividido el conjunto, y el numerador\(a\) representa cuántas partes se incluyen. El denominador,\(b\), no puede ser igual a cero porque la división por cero es indefinida.
En la Figura\(\PageIndex{4}\), el círculo se ha dividido en tres partes de igual tamaño. Cada parte representa\(\dfrac{1}{3}\) del círculo. Este tipo de modelo se llama círculo de fracción. Otras formas, como los rectángulos, también se pueden usar para modelar fracciones.
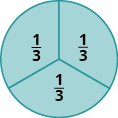
Figura\(\PageIndex{4}\)
¿Qué\(\dfrac{2}{3}\) representa la fracción? La fracción\(\dfrac{2}{3}\) significa dos de tres partes iguales.
Figura\(\PageIndex{5}\)
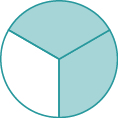
Nombra la fracción de la forma que se sombrea en cada una de las figuras.
Solución
Tenemos que hacer dos preguntas. Primero, ¿cuántas partes iguales hay? Este será el denominador. Segundo, de estas partes iguales, ¿cuántas están sombreadas? Este será el numerador.
| ¿Cuántas partes iguales hay? | Hay ocho partes iguales. |
| ¿Cuántos están sombreados? | Cinco partes están sombreadas. |
Cinco de cada ocho partes están sombreadas. Por lo tanto, la fracción del círculo que está sombreada es\(\dfrac{5}{8}\).
| ¿Cuántas partes iguales hay? | Hay nueve partes iguales. |
| ¿Cuántos están sombreados? | Dos partes están sombreadas. |
Dos de nueve partes están sombreadas. Por lo tanto, la fracción del cuadrado que está sombreada es\(\dfrac{2}{9}\).
Nombra la fracción de la forma que está sombreada en cada figura:
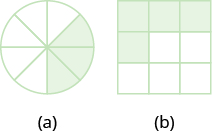
- Contestar a
-
\(\dfrac{3}{8}\)
- Respuesta b
-
\(\dfrac{4}{9}\)
Nombra la fracción de la forma que está sombreada en cada figura:
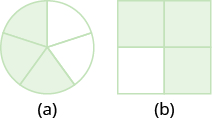
- Contestar a
-
\(\dfrac{3}{5}\)
- Respuesta b
-
\(\dfrac{3}{4}\)
Sombra\(\dfrac{3}{4}\) del círculo.

Solución
El denominador es\(4\), entonces dividimos el círculo en cuatro partes iguales (a). El numerador es\(3\), así que sombreamos tres de las cuatro partes (b).
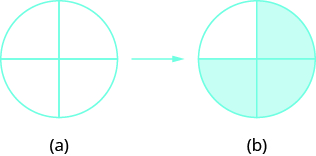
\(\dfrac{3}{4}\)del círculo está sombreado.
Sombra\(\dfrac{6}{8}\) del círculo.
- Contestar
-
Sombra\(\dfrac{2}{5}\) del rectángulo.

- Contestar
-

En Ejemplo\(\PageIndex{1}\) y Ejemplo\(\PageIndex{2}\), utilizamos círculos y rectángulos para modelar fracciones. Las fracciones también se pueden modelar como manipuladores llamados azulejos de fracción, como se muestra en la Figura\(\PageIndex{6}\). Aquí, el conjunto se modela como un azulejo rectangular largo, indiviso. Debajo hay baldosas de igual longitud divididas en diferentes números de partes de igual tamaño.
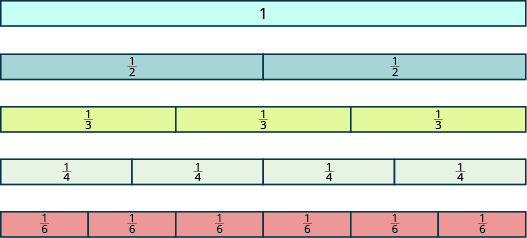
Figura\(\PageIndex{6}\)
Utilizaremos fichas de fracciones para descubrir algunos datos básicos sobre las fracciones. Consulte la Figura\(\PageIndex{6}\) para responder a las siguientes preguntas:
| ¿Cuántas\(\dfrac{1}{2}\) baldosas se necesitan para hacer una baldosa entera? | Se necesitan dos mitades para hacer un todo, así que dos de cada dos es\(\dfrac{2}{2}\) = 1. |
| ¿Cuántas\(\dfrac{1}{3}\) baldosas se necesitan para hacer una baldosa entera? | Se necesitan tres tercios, por lo que tres de cada tres es\(\dfrac{3}{3}\) = 1. |
| ¿Cuántas\(\dfrac{1}{4}\) baldosas se necesitan para hacer una baldosa entera? | Se necesitan cuatro cuartas partes, así que cuatro de cada cuatro es\(\dfrac{4}{4}\) = 1. |
| ¿Cuántas\(\dfrac{1}{5}\) baldosas se necesitan para hacer una baldosa entera? | Se necesitan seis sextos, por lo que seis de seis es\(\dfrac{6}{6}\) = 1. |
| ¿Y si el conjunto se dividiera en 24 partes iguales? (No hemos mostrado fichas de fracción para representar esto, pero trata de visualizarlo en tu mente). ¿Cuántas\(\dfrac{1}{24}\) baldosas se necesitan para hacer una baldosa entera? | Se necesitan 24 veinticuartas partes, por lo que\(\dfrac{24}{24}\) = 1. |
Se necesitan\(24\) veinticinco cuartas partes, entonces\(\dfrac{24}{24} = 1\). Esto nos lleva a la Propiedad de Uno.
Cualquier número, excepto cero, dividido por sí mismo es uno.
\[\dfrac{a}{a} = 1 \qquad \qquad (a \neq 0)\]
Usa círculos de fracción para hacer enteros usando las siguientes piezas:
- \(4\)cuartas
- \(5\)quintas
- \(6\)sextos
Solución
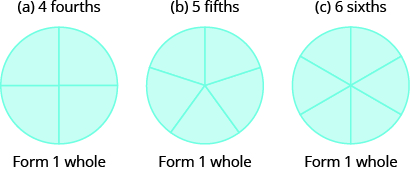
Usa círculos de fracción para hacer enteros con las siguientes piezas:\(3\) tercios.
- Contestar
-
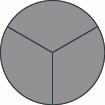
Use círculos de fracción para hacer enteros con las siguientes piezas:\(8\) octavos.
- Contestar
-
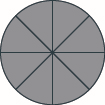
¿Y si tenemos más piezas de fracción de las que necesitamos para\(1\) enteros? Veremos esto en el siguiente ejemplo.
Usa círculos de fracción para hacer enteros usando las siguientes piezas:
- \(3\)mitades
- \(8\)quintas
- \(7\)tercios
Solución
- \(3\)las mitades se hacen\(1\) enteras con\(1\) la mitad sobrante.
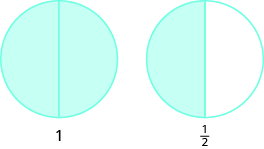
- \(8\)quintos hacen\(1\) enteros con\(3\) quintos sobrantes.
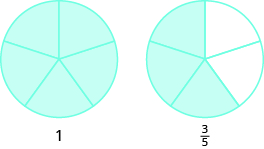
- \(7\)los tercios hacen\(2\) enteros con el\(1\) tercio sobrante.
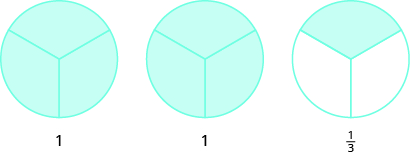
Usa círculos de fracción para hacer enteros con las siguientes piezas:\(5\) tercios.
- Contestar
-
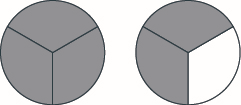
Usa círculos de fracciones para hacer enteros con las siguientes piezas:\(5\) mitades.
- Contestar
-
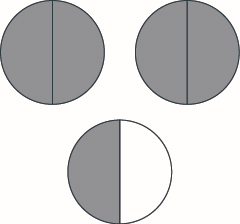
Modele fracciones impropias y números mixtos
En Ejemplo\(\PageIndex{4b}\), tenías ocho quintas piezas iguales. Usaste cinco de ellos para hacer uno entero, y te sobraron tres quintas partes. Usemos notación de fracciones para mostrar lo que sucedió. Tenías ocho piezas, cada una de ellas una quinta parte\(\dfrac{1}{5}\), así que en conjunto tenías ocho quintas partes, que podemos escribir como\(\dfrac{8}{5}\). La fracción\(\dfrac{8}{5}\) es un todo,\(1\), más tres quintos,\(\dfrac{3}{5}\), o\(1 \dfrac{3}{5}\), que se lee como uno y tres quintos.
El número\(1 \dfrac{3}{5}\) se llama un número mixto. Un número mixto consiste en un número entero y una fracción.
Un número mixto consiste en un número entero\(a\) y una fracción\(\dfrac{b}{c}\) donde\(c ≠ 0\). Está escrito de la siguiente manera.
\[a \dfrac{b}{c} \qquad \qquad c \neq 0\]
Las fracciones como\(\dfrac{5}{4}\),\(\dfrac{3}{2}\),\(\dfrac{5}{5}\), y\(\dfrac{7}{3}\) se denominan fracciones impropias. En una fracción impropia, el numerador es mayor o igual que el denominador, por lo que su valor es mayor o igual a uno. Cuando una fracción tiene un numerador que es menor que el denominador, se llama fracción propia, y su valor es menor que uno. Fracciones como\(\dfrac{1}{2}\),\(\dfrac{3}{7}\), y\(\dfrac{11}{18}\) son fracciones propias.
La fracción\(\dfrac{a}{b}\) es una fracción propia si\(a < b\) y una fracción impropia si\(a ≥ b\).
Nombra la fracción impropia modelada. Después escribe la fracción impropia como un número mixto.
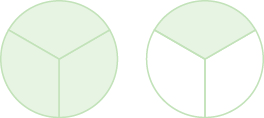
Solución
Cada círculo se divide en tres piezas, por lo que cada pieza es\(\dfrac{1}{3}\) del círculo. Hay cuatro piezas sombreadas, por lo que hay cuatro tercios o\(\dfrac{4}{3}\). La figura muestra que también tenemos un círculo entero y un tercio, que es\(1 \dfrac{1}{3}\). Entonces,\(\dfrac{4}{3} = 1 \dfrac{1}{3}\).
Nombra la fracción impropia. Después escríbelo como un número mixto.
- Contestar
-
\(\dfrac{5}{3}=1\dfrac{2}{3}\)
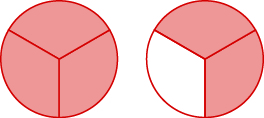
Nombra la fracción impropia. Después escríbelo como un número mixto.
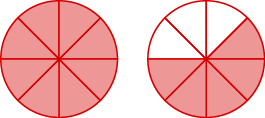
- Contestar
-
\(\dfrac{13}{8}=1\dfrac{5}{8}\)
Dibuja una figura para modelar\(\dfrac{11}{8}\).
Solución
El denominador de la fracción impropia es\(8\). Dibuja un círculo dividido en ocho piezas y sombrea todas ellas. Esto se encarga de ocho octavos, pero tenemos\(11\) octavos. Debemos sombrear tres de las ocho partes de otro círculo.
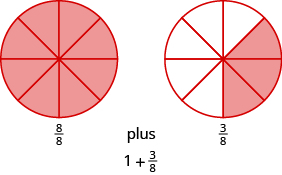
Entonces,\(\dfrac{11}{8} = 1 \dfrac{3}{8}\).
Dibuja una figura para modelar\(\dfrac{7}{6}\).
- Contestar
-
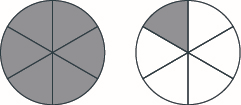
Dibuja una figura para modelar\(\dfrac{6}{5}\).
- Contestar
-
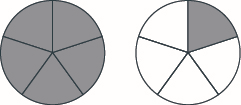
Utilice un modelo para reescribir la fracción impropia\(\dfrac{11}{6}\) como un número mixto.
Solución
Empezamos con\(11\) sextos\(\left(\dfrac{11}{6}\right)\). Sabemos que seis sextos hacen uno entero.
\[\dfrac{6}{6} = 1 \nonumber \]
Eso nos deja con cinco sextos más, que es\(\dfrac{5}{6}\) (11 sextos menos 6 sextos son 5 sextos). Entonces,\(\dfrac{11}{6} = 1 \dfrac{5}{6}\).
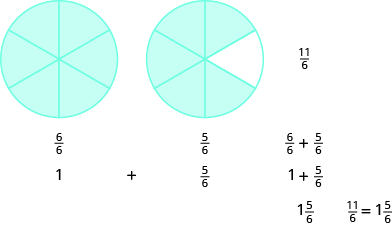
Utilice un modelo para reescribir la fracción impropia como un número mixto:\(\dfrac{9}{7}\).
- Contestar
-
\(1\dfrac{2}{7}\)
Utilice un modelo para reescribir la fracción impropia como un número mixto:\(\dfrac{7}{4}\).
- Contestar
-
\(1\dfrac{3}{4}\)
Utilice un modelo para reescribir el número mixto\(1 \dfrac{4}{5}\) como una fracción impropia.
Solución
El número mixto\(1 \dfrac{4}{5}\) significa un todo más cuatro quintos. El denominador es\(5\), así lo es el conjunto\(\dfrac{5}{5}\). Juntos cinco quintos y cuatro quintos equivalen a nueve quintos. Entonces,\(1 \dfrac{4}{5} = \dfrac{9}{5}\).
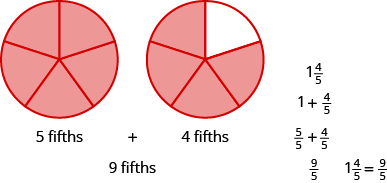
Utilice un modelo para reescribir el número mixto como una fracción impropia:\(1 \dfrac{3}{8}\).
- Contestar
-
\(\dfrac{11}{8}\)
Utilice un modelo para reescribir el número mixto como una fracción impropia:\(1 \dfrac{5}{6}\).
- Contestar
-
\(\dfrac{11}{6}\)
Convertir entre fracciones impropias y números mixtos
En Ejemplo\(\PageIndex{7}\), convertimos la fracción impropia\(\dfrac{11}{6}\) al número mixto\(1 \dfrac{5}{6}\) usando círculos de fracción. Esto lo hicimos agrupando seis sextos para hacer un todo; luego miramos para ver cuántas de las\(11\) piezas quedaban. Vimos que\(\dfrac{11}{6}\) hizo un grupo completo de seis sextos más cinco sextos más, demostrando eso\(\dfrac{11}{6} = \dfrac{15}{6}\).
La expresión de división\(\dfrac{11}{6}\) (que también se puede escribir como\(6 \overline{\smash{)}11}\)) nos dice encontrar cuántos grupos de\(6\) hay en\(11\). Para convertir una fracción impropia en un número mixto sin círculos de fracción, dividimos.
Convertir\(\dfrac{11}{6}\) a un número mixto.
Solución
| Divide el denominador en el numerador. | Recuerda\(\dfrac{11}{6}\) significa 11 ÷ 6. |
| Identificar el cociente, resto y divisor. | 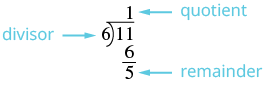 |
| Escribe el número mixto como\(quotient \dfrac{remainder}{divisor}\). | \(1 \dfrac{5}{6}\) |
Entonces,\(\dfrac{11}{6} = 1 \dfrac{5}{6}\).
Convertir la fracción impropia en un número mixto:\(\dfrac{13}{7}\).
- Contestar
-
\(1\dfrac{6}{7}\)
Convertir la fracción impropia en un número mixto:\(\dfrac{14}{9}\).
- Contestar
-
\(1\dfrac{5}{9}\)
Paso 1. Divide el denominador en el numerador.
Paso 2. Identificar el cociente, el resto y el divisor.
Paso 3. Escribe el número mixto como\(quotient \dfrac{remainder}{divisor}\).
Convertir la fracción impropia\(\dfrac{33}{8}\) a un número mixto.
Solución
| Divide el denominador en el numerador. | Recuerda,\(\dfrac{33}{8}\) significa\(8 \overline{\smash{)}33}\). |
| Identificar el cociente, el resto y el divisor. | 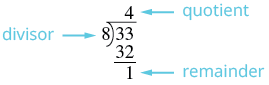 |
| Escribe el número mixto como\(quotient \dfrac{remainder}{divisor}\). | \(4 \dfrac{1}{8}\) |
Entonces,\(\dfrac{33}{8} = 4 \dfrac{1}{8}\).
Convertir la fracción impropia en un número mixto:\(\dfrac{23}{7}\).
- Contestar
-
\(3\dfrac{2}{7}\)
Convertir la fracción impropia en un número mixto:\(\dfrac{48}{11}\).
- Contestar
-
\(4\dfrac{4}{11}\)
En Ejemplo\(\PageIndex{8}\), cambiamos\(1 \dfrac{4}{5}\) a una fracción impropia al ver primero que el conjunto es un conjunto de cinco quintos. Entonces tuvimos cinco quintas y cuatro quintas más.
\[\dfrac{5}{5} + \dfrac{4}{5} = \dfrac{9}{5} \nonumber \]
¿De dónde salieron los nueve? Hay nueve quintos, un todo (cinco quintos) más cuatro quintos. Usemos esta idea para ver cómo convertir un número mixto en una fracción impropia.
Convertir el número mixto\(4 \dfrac{2}{3}\) en una fracción impropia.
| Multiplica el número entero por el denominador. | \(4 \dfrac{2}{3}\) |
| El número entero es 4 y el denominador es 3. | 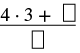 |
| Simplificar. | 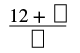 |
| Agrega el numerador al producto. | |
| El numerador del número mixto es 2. | 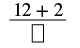 |
| Simplificar. | 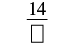 |
| Escribe la suma final sobre el denominador original. | |
| El denominador es 3. | \(\dfrac{14}{3}\) |
Convertir el número mixto en una fracción impropia:\(3 \dfrac{5}{7}\).
- Contestar
-
\(\dfrac{26}{7}\)
Convertir el número mixto en una fracción impropia:\(2 \dfrac{7}{8}\).
- Contestar
-
\(\dfrac{23}{8}\)
Paso 1. Multiplica el número entero por el denominador.
Paso 2. Agrega el numerador al producto que se encuentra en el Paso 1.
Paso 3. Escribe la suma final sobre el denominador original.
Convertir el número mixto\(10 \dfrac{2}{7}\) en una fracción impropia.
| Multiplica el número entero por el denominador. | \(10 \dfrac{2}{7}\) |
| El número entero es 10 y el denominador es 7. | 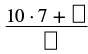 |
| Simplificar. | 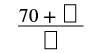 |
| Agrega el numerador al producto. | |
| El numerador del número mixto es 2. | 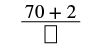 |
| Simplificar. | 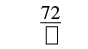 |
| Escribe la suma final sobre el denominador original. | |
| El denominador es 7. | \(\dfrac{72}{7}\) |
Convertir el número mixto en una fracción impropia:\(4 \dfrac{6}{11}\).
- Contestar
-
\(\dfrac{50}{11}\)
Convertir el número mixto en una fracción impropia:\(11 \dfrac{1}{3}\).
- Contestar
-
\(\dfrac{34}{3}\)