5.1: Decimales (Parte 1)
- Page ID
- 114282
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Nombrar decimales
- Escribir decimales
- Convertir decimales en fracciones o números mixtos
- Localizar decimales en la recta numérica*
- Ordene decimales
- Decimales redondos
Antes de comenzar, toma este cuestionario de preparación.
- Nombra el número 4,926,015 en palabras. Si te perdiste este problema, revisa el Ejemplo 1.1.4.
- Vuelta 748 al diez más cercano. Si te perdiste este problema, revisa el Ejemplo 1.2.9.
- Localizar\(\dfrac{3}{10}\) en una línea numérica. Si te perdiste este problema, revisa el Ejemplo 4.2.16.
Nombrar decimales
Probablemente ya conozcas bastante de decimales en función de tu experiencia con el dinero. Supongamos que compra un sándwich y una botella de agua para el almuerzo. Si el sándwich cuesta $3.45, la botella de agua cuesta $1.25, y el impuesto total a las ventas es de $0.33, ¿cuál es el costo total de tu almuerzo?
\[\begin{split} & $3.45 \qquad Sandwich \\ & $1.25 \qquad Water \\ + & $0.33 \qquad Tax \\ \hline & $5.03 \qquad Total \end{split}\]
El total es de $5.03. Supongamos que paga con una factura de $5 y 3 peniques. ¿Deberías esperar el cambio? No, $5 y 3 peniques es lo mismo que $5.03.
Debido a que 100 centavos = $1, cada centavo vale\(\dfrac{1}{100}\) de un dólar. Escribimos el valor de un centavo como $0.01, ya que 0.01 =\(\dfrac{1}{100}\).
Escribir un número con un decimal se conoce como notación decimal. Es una manera de mostrar partes de un todo cuando el todo es un poder de diez. En otras palabras, los decimales son otra forma de escribir fracciones cuyos denominadores son poderes de diez. Así como los números de conteo se basan en potencias de diez, los decimales se basan en potencias de diez. En la tabla se\(\PageIndex{1}\) muestran los números de conteo.
| Número de conteo | Nombre |
|---|---|
| 1 | Uno |
| 10 = 10 | Diez |
| 10 • 10 = 100 | Cien |
| 10 • 10 • 10 = 1000 | Mil |
| 10 • 10 • 10 • 10 = 10,000 | Diez mil |
¿Cómo se relacionan los decimales con las fracciones? En el cuadro se\(\PageIndex{2}\) muestra la relación.
| Decimal | Fracción | Nombre |
|---|---|---|
| 0.1 | \(\dfrac{1}{10}\) | Una décima |
| 0.01 | \(\dfrac{1}{100}\) | Centésimas |
| 0.001 | \(\dfrac{1}{1000}\) | Una milésima |
| 0.0001 | \(\dfrac{1}{10,000}\) | Una diezmilésima |
Cuando nombramos un número entero, el nombre corresponde al valor posicional basado en las potencias de diez. En Números Enteros aprendimos a leer 10,000 como diez mil. Asimismo, los nombres de los decimales corresponden a sus valores de fracción. Observe cómo los nombres del valor posicional en Figura\(\PageIndex{1}\) se relacionan con los nombres de las fracciones de la Tabla\(\PageIndex{2}\).
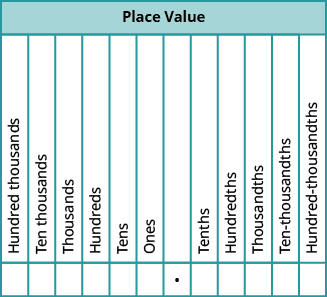
Figura\(\PageIndex{1}\) - Este gráfico ilustra los valores posicional a la izquierda y derecha del punto decimal.
Observe dos hechos importantes que se muestran en la Figura\(\PageIndex{1}\).
- El “th” al final del nombre significa que el número es una fracción. “Mil” es un número mayor que uno, pero “una milésima” es un número menor que uno.
- El décimo lugar es el primer lugar a la derecha del decimal, pero el lugar de las decenas es de dos lugares a la izquierda del decimal.
¿Recuerdas ese almuerzo de $5.03? Leemos $5.03 como cinco dólares y tres centavos. Nombrar decimales (aquellos que no representan dinero) se hace de manera similar. Leemos el número 5.03 como cinco y tres centésimas.
A veces necesitamos traducir a palabras un número escrito en notación decimal. Como se muestra en la Figura\(\PageIndex{2}\), escribimos el monto en un cheque tanto en palabras como en números.

Figura\(\PageIndex{2}\) - Cuando escribimos un cheque, escribimos la cantidad como un número decimal así como en palabras. El banco mira el cheque para asegurarse de que ambos números coincidan. Esto ayuda a prevenir errores.
| Intentemos nombrar un decimal, como 15.68. | |
| Empezamos por nombrar el número a la izquierda del decimal. | quince______ |
| Usamos la palabra “y” para indicar el punto decimal. | quince y_____ |
| Entonces nombramos el número a la derecha del punto decimal como si se tratara de un número entero. | quince y sesenta y ocho_____ |
| Apellido, nombra el lugar decimal del último dígito. | quince y sesenta y ocho centésimas |
El número 15.68 se lee quince y sesenta y ocho centésimas.
- Nombra el número a la izquierda del punto decimal.
- Escriba “y” para el punto decimal.
- Nombra la parte “número” a la derecha del punto decimal como si se tratara de un número entero.
- Nombra el lugar decimal del último dígito.
Nombrar cada decimal: (a) 4.3 (b) 2.45 (c) 0.009 (d) −15.571.
Solución
a) 4.3
| Nombra el número a la izquierda del punto decimal. | cuatro_____ |
| Escriba “y” para el punto decimal. | cuatro y_____ |
| Nombra el número a la derecha del punto decimal como si se tratara de un número entero. | cuatro y tres_____ |
| Nombra el lugar decimal del último dígito. | cuatro y tres décimas |
b) 2.45
| Nombra el número a la izquierda del punto decimal. | dos_____ |
| Escriba “y” para el punto decimal. | dos y_____ |
| Nombra el número a la derecha del punto decimal como si se tratara de un número entero. | dos y cuarenta y cinco_____ |
| Nombra el lugar decimal del último dígito. | dos y cuarenta y cinco centésimas |
(c) 0.009
| Nombra el número a la izquierda del punto decimal. | Cero es el número a la izquierda del decimal; no está incluido en el nombre. |
| Nombra el número a la derecha del punto decimal como si se tratara de un número entero. | nueve_____ |
| Nombra el lugar decimal del último dígito. | nueve milésimas |
(d) −15.571
| Nombra el número a la izquierda del punto decimal. | menos quince |
| Escriba “y” para el punto decimal. | quince negativos y_____ |
| Nombra el número a la derecha del punto decimal como si se tratara de un número entero. | menos quince quinientos setenta _____ |
| Nombra el lugar decimal del último dígito. | menos quince quinientos setenta y una milésimas |
Nombrar cada decimal: (a) 6.7 (b) 19.58 (c) 0.018 (d) −2.053
- Contestar a
-
seis y siete décimas
- Respuesta b
-
diecinueve y cincuenta y ocho centésimas
- Respuesta c
-
dieciocho milésimas
- Respuesta d
-
menos dos y cincuenta y tres milésimas
Nombrar cada decimal: (a) 5.8 (b) 3.57 (c) 0.005 (d) −13.461
- Contestar a
-
cinco y ocho décimas tres y cincuenta y siete centésimas
- Respuesta b
-
tres y cincuenta y siete centésimas
- Respuesta c
-
cinco milésimas
- Respuesta d
-
menos trece cuatrocientos sesenta y una milésimas
Escribir decimales
Ahora vamos a traducir el nombre de un número decimal a notación decimal. Revertiremos el procedimiento que acabamos de utilizar. Empecemos por escribir el número seis y diecisiete centésimas:
| La palabra y nos dice que coloquemos un punto decimal. | ___ . ___ |
| La palabra antes y es el número entero; escríbelo a la izquierda del punto decimal. | 6. _____ |
| La parte decimal es de diecisiete centésimas. Marcar dos lugares a la derecha del punto decimal para centésimas. | 6._ _ |
| Escribe los números para diecisiete en los lugares marcados. | 6.17 |
Escribe catorce y treinta y siete centésimas como decimal.
Solución
| Coloque un punto decimal debajo de la palabra 'y'. | ______ . _________ |
| Traduzca las palabras antes de 'y' al número entero y colóquelo a la izquierda del punto decimal. | 14. _________ |
| Marcar dos lugares a la derecha del punto decimal para “centésimas”. | 14.__ __ |
| Traduzca las palabras después de “y” y escriba el número a la derecha del punto decimal. | 14.37 |
Se escribe catorce y treinta y siete centésimas 14.37.
Escribir como decimal: trece y sesenta y ocho centésimas.
- Contestar
-
13.68
Escribir como decimal: quinientos ochocientos noventa y cuatro milésimas.
- Contestar
-
5.894
Paso 1. Busque la palabra “y” —localiza el punto decimal.
Paso 2. Marque el número de decimales necesarios a la derecha del punto decimal anotando el valor posicional indicado por la última palabra.
- Coloque un punto decimal debajo de la palabra “y”. Traduzca las palabras antes de “y” al número entero y colóquelo a la izquierda del punto decimal.
- Si no hay “y”, escribe un “0” con un punto decimal a su derecha.
Paso 3. Traducir las palabras después de “y” en el número a la derecha del punto decimal. Escribe el número en los espacios, poniendo el último dígito en el último lugar.
Paso 4. Rellene ceros para los portalugares según sea necesario.
La segunda bala en el Paso 2 es necesaria para decimales que no tienen parte de número entero, como 'nueve miles'. Los reconocemos por las palabras que indican el valor posicional después del decimal —como 'décimas' o 'centésimas'. Como no hay un número entero, no hay 'y'. Comenzamos colocando un cero a la izquierda del decimal y continuamos rellenando los números a la derecha, como hicimos arriba.
Escribe veinticuatro milésimas como decimal.
Solución
| Busca la palabra “y”. | No hay “y” así que empieza con 0. |
| A la derecha del punto decimal, ponga tres decimales para milésimas. |  |
| Escribe el número 24 con el 4 en el lugar milésimas. |  |
| Ponga ceros como marcadores de posición en los decimales restantes. | 0.024 |
Entonces, veinticuatro milésimas está escrito 0.024
Escribir como decimal: cincuenta y ocho milésimas.
- Contestar
-
0.058
Escribir como decimal: sesenta y siete milésimas.
- Contestar
-
0.067
Antes de pasar a nuestro siguiente objetivo, pensemos de nuevo en el dinero. Sabemos que $1 es lo mismo que $1.00. La forma en que escribimos $1 (o $1.00) depende del contexto. De la misma manera, los enteros pueden escribirse como decimales con tantos ceros como sea necesario a la derecha del decimal.
\[\begin{split} 5 & = 5.0 \qquad \quad -2 = -2.0 \\ 5 & = 5.00 \qquad \; \; -2 = -2.00 \\ 5 & = 5.000 \qquad -2 = -2.000 \\ & \qquad \qquad and \; so \; on \ldots \end{split}\]
Convertir decimales a fracciones o números mixtos
A menudo necesitamos reescribir decimales como fracciones o números mixtos. Volvamos a nuestro pedido de almuerzo para ver cómo podemos convertir los números decimales en fracciones. Sabemos que $5.03 significa 5 dólares y 3 centavos. Ya que hay 100 centavos en un dólar, 3 centavos la media\(\dfrac{3}{100}\) de un dólar, por lo que 0.03 =\(\dfrac{3}{100}\).
Convertimos decimales en fracciones identificando el valor posicional del dígito más lejano a la derecha. En el decimal 0.03, el 3 está en el lugar de centésimas, por lo que 100 es el denominador de la fracción equivalente a 0.03.
\[0.03 = \dfrac{3}{100} \nonumber\]
Para nuestro almuerzo de $5.03, podemos escribir el decimal 5.03 como un número mixto.
\[5.03 = 5 \dfrac{3}{100} \nonumber\]
Observe que cuando el número a la izquierda del decimal es cero, obtenemos una fracción propia. Cuando el número a la izquierda del decimal no es cero, obtenemos un número mixto.
Paso 1. Mira el número a la izquierda del decimal.
- Si es cero, el decimal se convierte en una fracción propia.
- Si no es cero, el decimal se convierte en un número mixto.
- Escribe el número entero.
Paso 2. Determinar el valor posicionar del dígito final.
Paso 3. Escribe la fracción.
- numerador—los 'números' a la derecha del punto decimal
- denominador—el valor posicional correspondiente al dígito final
Paso 4. Simplifique la fracción, si es posible.
Escribe cada uno de los siguientes números decimales como fracción o número mixto: (a) 4.09 (b) 3.7 (c) −0.286
Solución
(a) 4.09
| Hay un 4 a la izquierda del punto decimal. Escribe “4" como la parte del número entero del número mixto. |  |
| Determinar el valor posicionar del dígito final. |  |
| Escribe la fracción. Escribe 9 en el numerador ya que es el número a la derecha del punto decimal. |  |
| Escribe 100 en el denominador como el valor posicional del dígito final, 9, es centésima. | \(4 \dfrac{9}{100}\) |
| La fracción está en la forma más simple. | Entonces, 4.09 =\(4 \dfrac{9}{100}\) |
¿Notó que el número de ceros en el denominador es el mismo que el número de decimales?
b) 3.7
| Hay un 3 a la izquierda del punto decimal. Escribe “3" como la parte del número entero del número mixto. |  |
| Determinar el valor posicionar del dígito final. |  |
| Escribe la fracción. Escribe 7 en el numerador ya que es el número a la derecha del punto decimal. |  |
| Escribe 10 en el denominador como el valor posicional del dígito final, 7, es décimas. | \(3 \dfrac{7}{10}\) |
| La fracción está en la forma más simple. | Entonces, 3.7 =\(3 \dfrac{7}{10}\) |
(c) −0.286
| Hay un 0 a la izquierda del punto decimal. Escribe un signo negativo antes de la fracción. |  |
| Determinar el valor posicional del dígito final y escríbalo en el denominador. |  |
| Escribe la fracción. Escribe 286 en el numerador ya que es el número a la derecha del punto decimal. Escribe 1,000 en el denominador como el valor posicional del dígito final, 6, es milésimas. | \(- \dfrac{286}{1000}\) |
| Eliminamos un factor común de 2 para simplificar la fracción. | \(- \dfrac{143}{500}\) |
Escribir como fracción o número mixto. Simplifique la respuesta si es posible. (a) 5.3 (b) 6.07 (c) −0.234
- Contestar a
-
\(5 \frac{3}{10}\)
- Respuesta b
-
\(6 \frac{7}{100}\)
- Respuesta c
-
\(-\frac{234}{1000}\)
Escribir como fracción o número mixto. Simplifique la respuesta si es posible. (a) 8.7 (b) 1.03 (c) −0.024
- Contestar a
-
\(8 \frac{7}{10}\)
- Respuesta b
-
\(1 \frac{3}{100}\)
- Respuesta c
-
\(- \frac{24}{1000}\)


