5.2: Decimales (Parte 2)
- Page ID
- 114271
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Localizar decimales en la línea numérica
Dado que los decimales son formas de fracciones, ubicar decimales en la recta numérica es similar a ubicar fracciones en la recta numérica.
Localice 0.4 en una recta numérica.
Solución
El decimal 0.4 es equivalente a\(\dfrac{4}{10}\), por lo que 0.4 se ubica entre 0 y 1. En una recta numérica, divida el intervalo entre 0 y 1 en 10 partes iguales y coloque marcas para separar las partes.
Etiquete las marcas 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0. Escribimos 0 como 0.0 y 1 como 1.0, para que los números estén consistentemente en décimas. Por último, marque 0.4 en la recta numérica.

Localice 0.6 en una recta numérica.
- Contestar
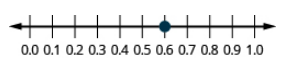
Localiza 0.9 en una recta numérica.
- Contestar
-
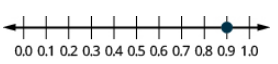
Localice −0.74 en una recta numérica.
Solución
El decimal −0.74 es equivalente a\(− \dfrac{74}{100}\), por lo que se ubica entre 0 y −1. En una recta numérica, marque y etiquete los múltiplos de -0.10 en el intervalo entre 0 y −1 (−0.10, −0.20, etc.) y marque −0.74 entre −0.70 y −0.80, un poco más cerca de −0.70.
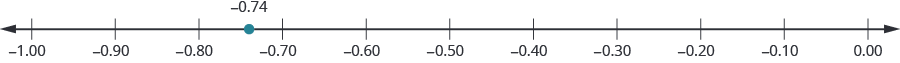
Localice −0.63 en una recta numérica.
- Contestar
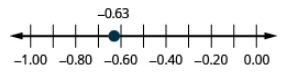
Localice −0.25 en una recta numérica.
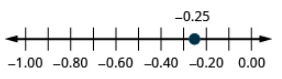
- Contestar
Orden de decimales
¿Cuál es mayor, 0.04 o 0.40?
Si piensas en esto como dinero, sabes que $0.40 (cuarenta centavos) es mayor que $0.04 (cuatro centavos). Entonces, 0.40 > 0.04.
En capítulos anteriores, se utilizó la línea numérica para ordenar números.
a < b: 'a es menor que b' cuando a está a la izquierda de b en la recta numérica
a > b: 'a es mayor que b' cuando a está a la derecha de b en la recta numérica
¿Dónde se encuentran 0.04 y 0.40 en la recta numérica?

Vemos que 0.40 está a la derecha de 0.04. Entonces sabemos 0.40 > 0.04.
¿Cómo se compara 0.31 con 0.308? Esto no se traduce en dinero para facilitar la comparación. Pero si convertimos 0.31 y 0.308 en fracciones, podemos decir cuál es mayor.
| 0.31 | 0.308 | |
| Convertir a fracciones. | $$\ dfrac {31} {100} $$ | $$\ dfrac {308} {1000} $$ |
| Necesitamos un denominador común para compararlos. | $$\ dfrac {31\ cdot\ textcolor {rojo} {10}} {100\ cdot\ textcolor {rojo} {10}} $$ | $$\ dfrac {308} {1000} $$ |
| $$\ dfrac {310} {1000} $$ | $$\ dfrac {308} {1000} $$ |
Porque 310 > 308, eso lo sabemos\(\dfrac{310}{1000} > \dfrac{308}{1000}\). Por lo tanto, 0.31 > 0.308.
Observe lo que hicimos al convertir 0.31 a una fracción, comenzamos con la fracción\(\dfrac{31}{100}\) y terminamos con la fracción equivalente\(\dfrac{310}{1000}\). Convertir de\(\dfrac{310}{1000}\) nuevo a un decimal da 0.310. Entonces 0.31 equivale a 0.310. Escribir ceros al final de un decimal no cambia su valor.
\[\dfrac{31}{100} = \dfrac{310}{1000} \quad and \quad 0.31 = 0.310\]
Si dos decimales tienen el mismo valor, se dice que son decimales equivalentes.
\[0.31 = 0.310\]
Decimos que 0.31 y 0.310 son decimales equivalentes.
Paso 1. Comprueba si ambos números tienen el mismo número de decimales. Si no, escribe ceros al final del que tenga menos dígitos para que coincidan.
Paso 2. Compara los números a la derecha del punto decimal como si fueran números enteros.
Paso 3. Ordene los números usando el signo de desigualdad apropiado.
Ordene los siguientes decimales usando < or >: (a) 0.64 __0.6 (b) 0.83 __0.803
Solución
a) 0.64 __0.6
| Comprueba si ambos números tienen el mismo número de decimales. No lo hacen, así que escribe uno cero a la derecha del 0.6. | 0.64 __0.60 |
| Compara los números a la derecha del punto decimal como si fueran números enteros. | 64 > 60 |
| Ordene los números usando el signo de desigualdad apropiado. |
0.64 > 0.60 0.64 > 0.6 |
b) 0.83 __0.803
| Comprueba si ambos números tienen el mismo número de decimales. No lo hacen, así que escribe uno cero a la derecha de 0.83. | 0.830 __0.803 |
| Compara los números a la derecha del punto decimal como si fueran números enteros. | 830 > 803 |
| Ordene los números usando el signo de desigualdad apropiado. |
0.830 > 0.803 0.83 > 0.803 |
Ordene cada uno de los siguientes pares de números, utilizando < or >: (a) 0.42__0.4 (b) 0.76__0.706
- Contestar a
-
>
- Respuesta b
-
>
Ordene cada uno de los siguientes pares de números, utilizando < or >: (a) 0.1__0.18 (b) 0.305__0.35
- Contestar a
-
<
- Respuesta b
-
<
Cuando ordenamos decimales negativos, es importante recordar cómo ordenar enteros negativos. Recordemos que los números más grandes están a la derecha en la recta numérica. Por ejemplo, debido a que −2 se encuentra a la derecha de −3 en la recta numérica, sabemos que −2 > −3. Del mismo modo, los números más pequeños se encuentran a la izquierda en la recta numérica. Por ejemplo, debido a que −9 se encuentra a la izquierda de −6 en la recta numérica, sabemos que −9 < −6.
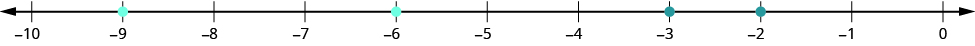
Si acercamos el intervalo entre 0 y −1, veríamos de la misma manera que −0.2 > −0.3 y −0.9 < −0.6.
< or >Utilícelo para ordenar. −0.1__−0.8.
Solución
| Escribe los números uno debajo del otro, alineando los puntos decimales. |
−0.1 −0.8 |
| Tienen el mismo número de dígitos. | |
| Dado que −1 > −8, −1 décima es mayor que −8 décimas. | −0.1 > −0.8 |
Ordene cada uno de los siguientes pares de números, usando < or >: −0.3___−0.5
- Contestar
-
>
Ordene cada uno de los siguientes pares de números, usando < or >: −0.6___−0.7
- Contestar
-
>
Decimales Redondos
En Estados Unidos, los precios de la gasolina suelen escribirse con la parte decimal como milésimas de dólar. Por ejemplo, una gasolinera podría registrar el precio del gas sin plomo en $3.279 por galón. Pero si compraras exactamente un galón de gasolina a este precio, pagarías $3.28, porque el precio final se redondearía al centavo más cercano. En Números Enteros, vimos que redondeamos números para obtener un valor aproximado cuando no se necesita el valor exacto. Supongamos que quisiéramos redondear $2.72 al dólar más cercano. ¿Está más cerca de $2 o de $3? ¿Y si quisiéramos redondear $2.72 a los diez centavos más cercanos; ¿está más cerca de $2.70 o a $2.80? Las líneas numéricas en Figura\(\PageIndex{3}\) pueden ayudarnos a responder esas preguntas.

Figura\(\PageIndex{3}\) - (b) Vemos que 2.72 está más cerca de 3 que de 2. Entonces, 2.72 redondeado al número entero más cercano es 3. b) Vemos que 2.72 está más cerca de 2.70 que 2.80. Entonces decimos que 2.72 redondeado al décimo más cercano es 2.7.
¿Podemos redondear decimales sin líneas numéricas? ¡Sí! Utilizamos un método basado en el que usamos para redondear números enteros.
Paso 1. Localice el valor posicional dado y márquelo con una flecha.
Paso 2. Subrayar el dígito a la derecha del valor posicional dado.
Paso 3. ¿Este dígito es mayor o igual a 5?
- Sí - suma 1 al dígito en el valor posicional dado.
- No - no cambie el dígito en el valor posicional dado
Paso 4. Reescribe el número, eliminando todos los dígitos a la derecha del valor posicional dado.
Vuelta 18.379 a la centésima más cercana.
Solución
| Localice el lugar centésimas y márquelo con una flecha. |  |
| Subrayar el dígito a la derecha del 7. | 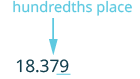 |
| Debido a que 9 es mayor o igual a 5, agregue 1 al 7. |  |
| Reescribe el número, eliminando todos los dígitos a la derecha del lugar centésimas. | 18.38 |
18.38 es 18.379 redondeado a la centésima más cercana.
Vuelta a la centésima más cercana: 1.047.
- Contestar
-
1.05
Vuelta a la centésima más cercana: 9.173.
- Contestar
-
9.17
Circular 18.379 al número entero más cercano (a) décimo (b).
Solución
a) Circular 18.379 a la décima más cercana.
| Localiza el décimo lugar y márcalo con una flecha. |  |
| Subrayar el dígito a la derecha del dígito décimo. |  |
| Debido a que 7 es mayor o igual a 5, agregue 1 al 3. |  |
| Reescribe el número, eliminando todos los dígitos a la derecha del lugar décimas. | 18.4 |
Entonces, 18.379 redondeado al décimo más cercano es 18.4.
b) Circular 18.379 al número entero más cercano.
| Localice el lugar de los unos y márquelo con una flecha. | 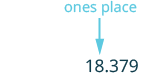 |
| Subrayar el dígito a la derecha del lugar unos. |  |
| Dado que 3 no es mayor ni igual a 5, no agregue 1 al 8. |  |
| Reescribe el número, eliminando todos los dígitos a la derecha del lugar de unos. | 18 |
Por lo que 18.379 redondeado al número entero más cercano es 18.
Redondear 6.582 al número entero más cercano (a) centésima (b) décima (c).
- Contestar a
-
6.58
- Respuesta b
-
6.6
- Respuesta c
-
7
Vuelta 15.2175 a la más cercana (a) milésima (b) centésima (c) décima.
- Contestar a
-
15.218
- Respuesta b
-
15.22
- Respuesta c
-
15.2
La práctica hace la perfección
Nombre Decimales En los siguientes ejercicios, nombra cada decimal.
- 5.5
- 7.8
- 5.01
- 14.02
- 8.71
- 2.64
- 0.002
- 0.005
- 0.381
- 0.479
- −17.9
- −31.4
Escribir decimales
En los siguientes ejercicios, traduzca el nombre a un número decimal.
- Ocho y tres centésimas
- Nueve y siete centésimas
- Veintinueve y ochenta y una centésimas
- Sesenta y uno setenta y cuatro centésimas
- Siete décimas
- Seis décimas
- Una milésima
- Nueve milésimas
- Veintinueve milésimas
- Treinta y cinco milésimas
- Once y nueve diez milésimas negativas
- Negativo cincuenta y nueve y dos diezmilésimas
- Trece trescientos noventa y cinco diez milésimas
- Treinta y doscientos setenta y nueve milésimas
Convertir decimales a fracciones o números mixtos
En los siguientes ejercicios, convierte cada decimal a una fracción o número mixto.
- 1.99
- 5.83
- 15.7
- 18.1
- 0.239
- 0.373
- 0.13
- 0.19
- 0.011
- 0.049
- −0.00007
- −0.00003
- 6.4
- 5.2
- 7.05
- 9.04
- 4.006
- 2.008
- 10.25
- 12.75
- 1.324
- 2.482
- 14.125
- 20.375
Localizar decimales en la línea numérica
En los siguientes ejercicios, ubique cada número en una recta numérica.
- 0.8
- 0.3
- −0.2
- −0.9
- 3.1
- 2.7
- −2.5
- −1.6
Orden de decimales
En los siguientes ejercicios, ordene cada uno de los siguientes pares de números, utilizando < or >.
- 0.9__0.6
- 0.7__0.8
- 0.37__0.63
- 0.86__0.69
- 0.6__0.59
- 0.27__0.3
- 0.91__0.901
- 0.415__0.41
- −0.5__−0.3
- −0.1_−0.4
- −0.62_−0.619
- −7.31_−7.3
Decimales Redondos
En los siguientes ejercicios, redondear cada número al décimo más cercano.
- 0.67
- 0.49
- 2.84
- 4.63
En los siguientes ejercicios, redondear cada número a la centésima más cercana.
- 0.845
- 0.761
- 5.7932
- 3.6284
- 0.299
- 0.697
- 4.098
- 7.096
En los siguientes ejercicios, redondea cada número al número entero más cercano (a) centésima (b) décima (c).
- 5.781
- 1.638
- 63.479
- 84.281
Matemáticas cotidianas
- Incremento salarial Danny obtuvo un aumento y ahora gana $58,965.95 al año. Redondear este número al más cercano: a) dólar (b) mil dólares (c) diez mil dólares.
- Nuevo Compra de auto nuevo El auto nuevo de Selena costó $23,795.95. Redondear este número al más cercano: a) dólar (b) mil dólares (c) diez mil dólares.
- Impuesto a las ventas Hyo Jin vive en San Diego. Ella compró un refrigerador por $1624.99 y cuando el empleado calculó el impuesto a las ventas salió exactamente a $142.186625. Redondear el impuesto sobre las ventas al (a) centavo (b) dólar más cercano.
- Impuesto sobre las ventas Jennifer compró un juego de comedor de $1,038.99 para su casa en Cincinnati. Ella calculó que el impuesto a las ventas era exactamente de 67.53435 dólares. Redondear el impuesto sobre las ventas al (a) centavo (b) dólar más cercano.
Ejercicios de escritura
- ¿Cómo te ayuda tu conocimiento del dinero a aprender sobre los decimales?
- Explica cómo escribes “tres y nueve centésimas” como decimal.
- Jim corrió una carrera de 100 metros en 12.32 segundos. Tim corrió la misma carrera en 12.3 segundos. ¿Quién tuvo el tiempo más rápido, Jim o Tim? ¿Cómo lo sabes?
- Gerry vio un letrero anunciando postales marcadas a la venta en “10 por 0.99¢”. ¿Qué tiene de malo el precio anunciado?
Autocomprobación
(a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.
(b) Si la mayoría de sus cheques fueron:
... con confianza. ¡Felicidades! Has logrado los objetivos en esta sección. Reflexiona sobre las habilidades de estudio que usaste para que puedas seguir usándolas. ¿Qué hiciste para confiar en tu capacidad para hacer estas cosas? Ser específico.
... con alguna ayuda. Esto debe abordarse rápidamente porque los temas que no dominas se convierten en baches en tu camino hacia el éxito. En matemáticas, cada tema se basa en trabajos anteriores. Es importante asegurarse de tener una base sólida antes de seguir adelante. ¿A quién puedes pedir ayuda? Tus compañeros de clase e instructor son buenos recursos. ¿Hay algún lugar en el campus donde estén disponibles los tutores de matemáticas? ¿Se pueden mejorar tus habilidades de estudio?
... no, ¡no lo comprendo! Esta es una señal de advertencia y no debes ignorarla. Debería obtener ayuda de inmediato o rápidamente se verá abrumado. Consulte a su instructor lo antes posible para discutir su situación. Juntos pueden idear un plan para obtener la ayuda que necesita.


