11.4: Graficar ecuaciones lineales (Parte 2)
- Page ID
- 114234
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Gráfica líneas verticales y horizontales
¿Podemos graficar una ecuación con una sola variable? Sólo x y no y, o simplemente y sin una x? ¿Cómo haremos una tabla de valores para obtener los puntos para trazar?
Consideremos la ecuación x = −3. La ecuación dice que x siempre es igual a −3, por lo que su valor no depende de y No importa lo que sea y, el valor de x siempre es −3.
Para hacer una tabla de soluciones, escribimos −3 para todos los valores x. Entonces elige cualquier valor para y. ya que x no depende de y, puedes elegir cualquier número que te guste. Pero para ajustar el tamaño de nuestra gráfica de coordenadas, usaremos 1, 2 y 3 para las coordenadas y como se muestra en la tabla.
| x = -3 | ||
|---|---|---|
| x | y | (x, y) |
| -3 | 1 | (-3, 1) |
| -3 | 2 | (-3, 2) |
| -3 | 3 | (-3, 3) |
Después, trazar los puntos y conectarlos con una línea recta. Observe en la Figura\(\PageIndex{5}\) que la gráfica es una línea vertical.
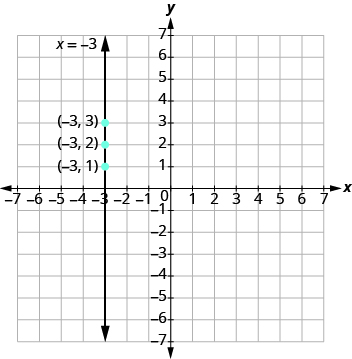
Figura\(\PageIndex{5}\)
Una línea vertical es la gráfica de una ecuación que se puede escribir en la forma x = a La línea pasa por el eje x en (a, 0).
Grafica la ecuación x = 2. ¿Qué tipo de línea forma?
Solución
La ecuación tiene solo variable, x, y x siempre es igual a 2. Hacemos una tabla donde x es siempre 2 y ponemos cualquier valor para y.
| x = -3 | ||
|---|---|---|
| x | y | (x, y) |
| 2 | 1 | (2, 1) |
| 2 | 2 | (2, 2) |
| 2 | 3 | (2, 3) |
Trazar los puntos y conectarlos como se muestra.
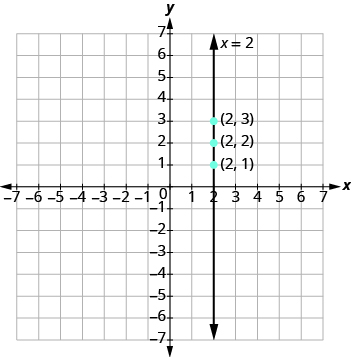
La gráfica es una línea vertical que pasa por el eje x en 2.
Grafica la ecuación: x = 5.
- Contestar
-
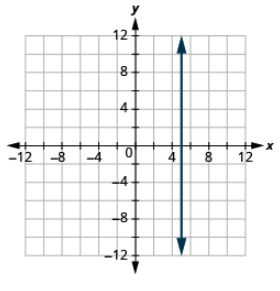
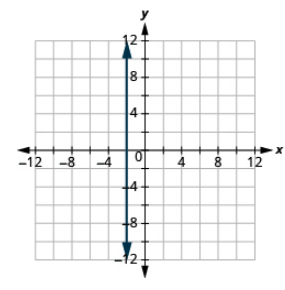
Grafica la ecuación: x = −2.
- Contestar
-
¿Y si la ecuación tiene y pero no x? Vamos a graficar la ecuación y = 4. Esta vez el valor y es una constante, por lo que en esta ecuación y no depende de x.
Para hacer una tabla de soluciones, escriba 4 para todos los valores y y luego elija cualquier valor para x.
Usaremos 0, 2 y 4 para los valores x.
| x = -3 | ||
|---|---|---|
| x | y | (x, y) |
| 0 | 4 | (0, 4) |
| 2 | 4 | (2, 4) |
| 4 | 4 | (4, 4) |
Trazar los puntos y conectarlos, como se muestra en la Figura\(\PageIndex{6}\). Esta gráfica es una línea horizontal que pasa por el eje y en 4.
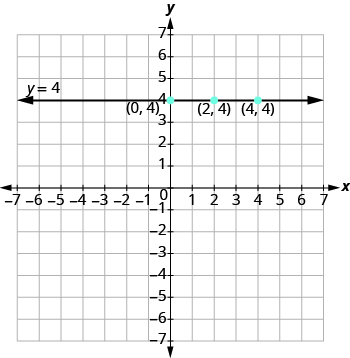
Figura\(\PageIndex{6}\)
Una línea horizontal es la gráfica de una ecuación que se puede escribir en la forma y = b La línea pasa por el eje y en (0, b).
Grafica la ecuación y = −1.
Solución
La ecuación y = −1 solo tiene variable, y. El valor de y es constante. Todos los pares ordenados en la tabla tienen la misma coordenada y, −1. Elegimos 0, 3 y −3 como valores para x.
| x = -3 | ||
|---|---|---|
| x | y | (x, y) |
| -3 | -1 | (-3, -1) |
| 0 | -1 | (0, -1) |
| 3 | -1 | (3, -1) |
La gráfica es una línea horizontal que pasa por el eje y en —1 como se muestra.
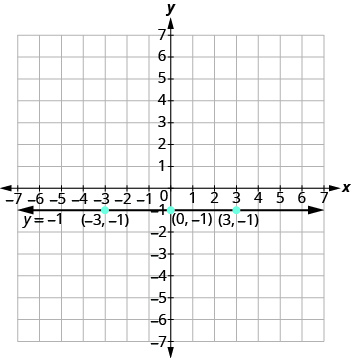
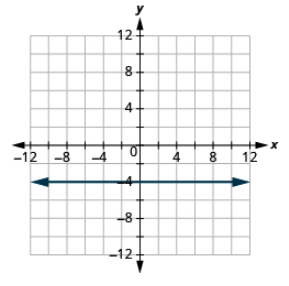
Grafica la ecuación: y = −4.
- Contestar
-
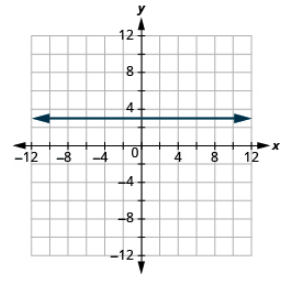
Grafica la ecuación: y = 3.
- Contestar
-
Las ecuaciones para líneas verticales y horizontales se ven muy similares a ecuaciones como y = 4x. ¿Cuál es la diferencia entre las ecuaciones y = 4x e y = 4?
La ecuación y = 4x tiene tanto x como y. El valor de y depende del valor de x. La coordenada y cambia según el valor de x.
La ecuación y = 4 tiene sólo una variable. El valor de y es constante. La coordenada y es siempre 4. No depende del valor de x.
| y = 4x | ||
|---|---|---|
| x | y | (x, y) |
| 0 | 0 | (0, 0) |
| 1 | 4 | (1, 4) |
| 2 | 8 | (2, 8) |
| \(\textcolor{red}{y = 4}\) | ||
|---|---|---|
| \ (\ textcolor {rojo} {y = 4}\) "> x | y | (x, y) |
| \ (\ textcolor {rojo} {y = 4}\) ">0 | 4 | (0, 4) |
| \ (\ textcolor {rojo} {y = 4}\) ">1 | 4 | (1, 4) |
| \ (\ textcolor {rojo} {y = 4}\) ">2 | 4 | (2, 4) |
La gráfica muestra ambas ecuaciones.
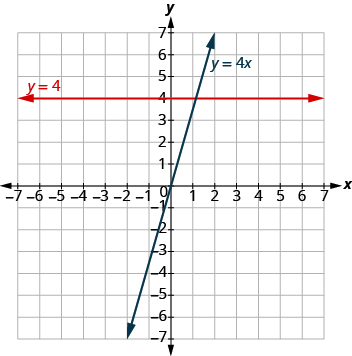
Observe que la ecuación y = 4x da una línea inclinada mientras que y = 4 da una línea horizontal.
Gráfica y = −3x e y = −3 en el mismo sistema de coordenadas rectangulares.
Solución
Encuentra tres soluciones para cada ecuación. Observe que la primera ecuación tiene la variable x, mientras que la segunda no. Se listan soluciones para ambas ecuaciones.
| \(\textcolor{red}{y = -3x}\) | ||
|---|---|---|
| \ (\ textcolor {rojo} {y = -3x}\) "> x | y | (x, y) |
| \ (\ textcolor {rojo} {y = -3x}\) ">0 | 0 | (0, 0) |
| \ (\ textcolor {rojo} {y = -3x}\) ">1 | -3 | (1, -3) |
| \ (\ textcolor {rojo} {y = -3x}\) ">2 | -6 | (2, -6) |
| y = -3 | ||
|---|---|---|
| x | y | (x, y) |
| 0 | -3 | (0, -3) |
| 1 | -3 | (1, -3) |
| 2 | -3 | (2, -3) |
La gráfica muestra ambas ecuaciones.
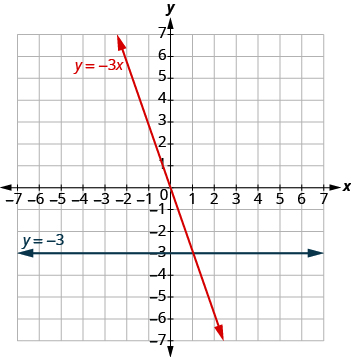
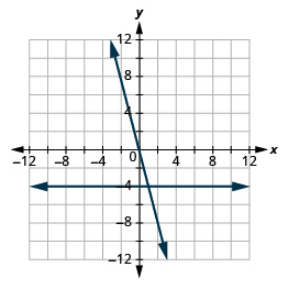
Grafica las ecuaciones en el mismo sistema de coordenadas rectangulares: y = −4x e y = −4.
- Contestar
-
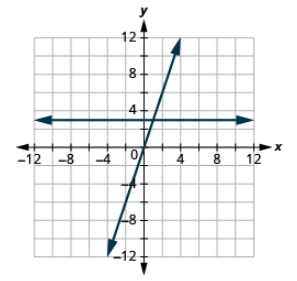
Grafica las ecuaciones en el mismo sistema de coordenadas rectangulares: y = 3 e y = 3x.
- Contestar
-
La práctica hace la perfección
Reconocer la relación entre las soluciones de una ecuación y su gráfica
Para cada par ordenado, decide (a) ¿es el par ordenado una solución a la ecuación? b) ¿El punto está en la línea?
- y = x + 2
- (0, 2)
- (1, 2)
- (− 1, 1)
- (− 3, 1)
- y = x − 4
- (0, − 4)
- (3, − 1)
- (2, 2)
- (1, − 5)
- y =\(\dfrac{1}{2}\) x − 3
- (0, − 3)
- (2, − 2)
- (− 2, − 4)
- (4, 1)
- y =\(\dfrac{1}{3}\) x + 2
- (0, 2)
- (3, 3)
- (− 3, 2)
- (− 6, 0)
Graficar una ecuación lineal trazando puntos
En los siguientes ejercicios, grafica por puntos de trazado.
- y = 3x − 1
- y = 2x + 3
- y = −2x + 2
- y = −3x + 1
- y = x + 2
- y = x − 3
- y = − x − 3
- y = − x − 2
- y = 2x
- y = 3x
- y = −4x
- y = −2x
- y =\(\dfrac{1}{2}\) x + 2
- y =\(\dfrac{1}{3}\) x − 1
- y =\(\dfrac{4}{3}\) x − 5
- y =\(\dfrac{3}{2}\) x − 3
- y =\(− \dfrac{2}{5}\) x + 1
- y =\(− \dfrac{4}{5}\) x − 1
- y =\(− \dfrac{3}{2}\) x + 2
- y =\(− \dfrac{5}{3}\) x + 4
- x + y = 6
- x + y = 4
- x + y = −3
- x + y = −2
- x − y = 2
- x − y = 1
- x − y = −1
- x − y = −3
- −x + y = 4
- −x + y = 3
- −x − y = 5
- −x − y = 1
- 3x + y = 7
- 5x + y = 6
- 2x + y = −3
- 4x + y = −5
- 2x + 3 años = 12
- 3x − 4 años = 12
- \(\dfrac{1}{3}\)x + y = 2
- \(\dfrac{1}{2}\)x + y = 3
Gráfica líneas verticales y horizontales
En los siguientes ejercicios, grafica las líneas verticales y horizontales.
- x = 4
- x = 3
- x = −2
- x = −5
- y = 3
- y = 1
- y = −5
- y = −2
- x =\(\dfrac{7}{3}\)
- x =\(\dfrac{5}{4}\)
En los siguientes ejercicios, grafica cada par de ecuaciones en un mismo sistema de coordenadas rectangulares.
- y =\(− \dfrac{1}{2}\) x e y =\(− \dfrac{1}{2}\)
- y =\(− \dfrac{1}{3}\) x e y =\(− \dfrac{1}{3}\)
- y = 2x e y = 2
- y = 5x e y = 5
Práctica Mixta
En los siguientes ejercicios, grafica cada ecuación.
- y = 4x
- y = 2x
- y =\(− \dfrac{1}{2}\) x + 3
- y =\(\dfrac{1}{4}\) x − 2
- y = − x
- y = x
- x − y = 3
- x + y = − 5
- 4x + y = 2
- 2x + y = 6
- y = −1
- y = 5
- 2x + 6 años = 12
- 5x + 2 años = 10
- x = 3
- x = −4
Matemáticas cotidianas
- Costo de la autocasa Los Robinsons rentaron una casa rodante por una semana para irse de vacaciones. Les costó $594 más $0.32 por milla para rentar la autocasa, por lo que la ecuación lineal y = 594 + 0.32x da el costo, y, por conducir x millas. Calcule el costo de alquiler para conducir 400, 800 y 1,200 millas, y luego graficar la línea.
- Ganancia semanal En la galería de arte donde trabaja, a Salvador se le pagan $200 semanales más el 15% de las ventas que realiza, por lo que la ecuación y = 200 + 0.15x da la cantidad y que gana por vender x dólares de obra de arte. Calcula la cantidad que Salvador gana por vender $900, $1,600 y $2,000, y luego grafica la línea.
Ejercicios de escritura
- Explica cómo elegirías tres valores x para hacer una tabla para graficar la línea y =\(\dfrac{1}{5}\) x − 2.
- ¿Cuál es la diferencia entre las ecuaciones de una línea vertical y una horizontal?
Autocomprobación
(a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

(b) Después de revisar esta lista de verificación, ¿qué hará para confiar en todos los objetivos?


