11.3: Graficar ecuaciones lineales (Parte 1)
- Page ID
- 114224
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Reconocer la relación entre las soluciones de una ecuación y su gráfica
- Graficar una ecuación lineal trazando puntos
- Graficar líneas verticales y horizontales
Antes de comenzar, toma este cuestionario de preparación.
- Evaluar: 3x + 2 cuando x = −1. Si te perdiste este problema, revisa el Ejemplo 3.8.10.
- Resuelve la fórmula: 5x + 2y = 20 para y. Si te perdiste este problema, revisa Ejemplo 9.11.6.
- Simplificar:\(\dfrac{3}{8}\) (−24). Si te perdiste este problema, revisa el Ejemplo 4.3.10.
Reconocer la relación entre las soluciones de una ecuación y su gráfica
En Uso del Sistema de Coordenadas Rectangulares, encontramos algunas soluciones a la ecuación 3x + 2y = 6. Se enumeran en la siguiente tabla. Entonces, los pares ordenados (0, 3), (2, 0),\(\left(1, \dfrac{3}{2}\right)\), (4, − 3), son algunas soluciones a la ecuación 3x + 2y = 6. Podemos trazar estas soluciones en el sistema de coordenadas rectangulares como se muestra en la gráfica de la derecha.

¿Observa cómo se alinean perfectamente los puntos? Conectamos los puntos con una línea recta para obtener la gráfica de la ecuación 3x + 2y = 6. Observe las flechas en los extremos de cada lado de la línea. Estas flechas indican que la línea continúa.

Cada punto de la línea es una solución de la ecuación. Además, cada solución de esta ecuación es un punto en esta línea. ¡Los puntos que no están en la línea no son soluciones!
Observe que el punto cuyas coordenadas son (− 2, 6) está en la línea que se muestra en la Figura\(\PageIndex{1}\). Si sustituye x = − 2 e y = 6 en la ecuación, encuentra que es una solución a la ecuación.

Figura\(\PageIndex{1}\)
Entonces (4, 1) no es una solución a la ecuación 3x + 2y = 6. Por lo tanto el punto (4, 1) no está en la línea. Este es un ejemplo del dicho: “Una imagen vale más que mil palabras”. La línea te muestra todas las soluciones a la ecuación. Cada punto de la línea es una solución de la ecuación. Y, cada solución de esta ecuación está en esta línea. Esta línea se llama la gráfica de la ecuación 3x + 2y = 6.
La gráfica de una ecuación lineal Ax + By = C es una línea recta.
- Cada punto de la línea es una solución de la ecuación.
- Toda solución de esta ecuación es un punto en esta línea.
A continuación se muestra la gráfica de y = 2x − 3.

Por cada par ordenado decide (a) ¿El par ordenado es una solución a la ecuación? b) ¿El punto está en la línea?
(a) (0, 3) (b) (3, − 3) (c) (2, − 3) (d) (− 1, − 5)
Solución
Sustituya los valores x e y en la ecuación para verificar si el par ordenado es una solución a la ecuación.
a)\[\begin{split} (a)&\; (\textcolor{blue}{0}, \textcolor{red}{-3}) \qquad \qquad \quad \; (b)\; (\textcolor{blue}{3}, \textcolor{red}{3}) \qquad \qquad \qquad \quad (c)\; (\textcolor{blue}{2}, \textcolor{red}{-3}) \qquad \qquad \qquad \quad (d)\; (\textcolor{blue}{-1}, \textcolor{red}{-5}) \\ y &= 2x - 3 \qquad \qquad \quad y = 2x - 3 \qquad \qquad \qquad \; y = 2x - 3 \qquad \qquad \qquad \; \; \; y = 2x - 3 \\ \textcolor{red}{-3} &\stackrel{?}{=} 2(\textcolor{blue}{0}) - 3 \qquad \qquad \; \textcolor{red}{3} \stackrel{?}{=} 2(\textcolor{blue}{3}) - 3 \qquad \qquad \; \textcolor{red}{-3} \stackrel{?}{=} 2(\textcolor{blue}{2}) - 3 \qquad \qquad \; \; \; \textcolor{red}{-5} \stackrel{?}{=} 2(\textcolor{blue}{-1}) - 3 \\ -3 &= -3\; \checkmark \qquad \qquad \quad \; \; 3 = 3\; \checkmark \qquad \qquad \qquad -3 \neq 1 \qquad \qquad \qquad \qquad -5 = -5\; \checkmark \\ (0, -3)\;& is\; a\; solution \ldotp \quad (3, 3)\; is\; a\; solution \ldotp \qquad (2, -3)\; is\; not\; a\; solution \ldotp \qquad (-1, -5)\; is\; a\; solution \ldotp \end{split}\]
b) Trazar los puntos A: (0, − 3) B: (3, 3) C: (2, − 3) y D: (− 1, − 5). Los puntos (0, − 3), (3, 3) y (− 1, − 5) están en la línea y = 2x − 3, y el punto (2, − 3) no está en la línea.

Los puntos que son soluciones a y = 2x − 3 están en la línea, pero el punto que no es una solución no está en la línea.
Se muestra la gráfica de y = 3x − 1. Para cada par ordenado, decide (a) ¿es el par ordenado una solución a la ecuación? b) ¿El punto está en la línea?

- (0, − 1)
- (2, 2)
- (3, − 1)
- (− 1, − 4)
- Respuesta 1.
-
a. si, b. no
- Respuesta 2.
-
a. no, b. no
- Respuesta 3.
-
a. no, b. no
- Respuesta 4.
-
a. si, b. si
Graficar una ecuación lineal trazando puntos
Existen varios métodos que se pueden utilizar para graficar una ecuación lineal. El método que utilizamos al inicio de esta sección para graficar se llama puntos de trazado, o Método de Trazado de Puntos.
Vamos a graficar la ecuación y = 2x + 1 trazando puntos. Comenzamos por encontrar tres puntos que son soluciones a la ecuación. Podemos elegir cualquier valor para x o y, luego, resolver para la otra variable.
Dado que y está aislado en el lado izquierdo de la ecuación, es más fácil elegir valores para x. Usaremos 0, 1 y -2 para x para este ejemplo. Sustituimos cada valor de x en la ecuación y resolvemos por y.

Podemos organizar las soluciones en una mesa. Ver Tabla\(\PageIndex{1}\).
| y = 2x + 1 | ||
|---|---|---|
| x | y | (x, y) |
| 0 | 1 | (0, 1) |
| 1 | 3 | (1, 3) |
| -2 | -3 | (-2, -3) |
Ahora trazamos los puntos en un sistema de coordenadas rectangular. Comprueba que los puntos se alineen. Si no se alineaban, significaría que cometimos un error y deberíamos volver a verificar todo nuestro trabajo. Ver Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\)
Dibuja la línea a través de los tres puntos. Extiende la línea para llenar la cuadrícula y coloca flechas en ambos extremos de la línea. La línea es la gráfica de y = 2x + 1.

Figura\(\PageIndex{3}\)
Paso 1. Encuentra tres puntos cuyas coordenadas son soluciones a la ecuación. Organizarlos en una mesa.
Paso 2. Trazar los puntos en un sistema de coordenadas rectangulares. Comprueba que los puntos se alineen. Si no lo hacen, revisa cuidadosamente tu trabajo.
Paso 3. Dibuja la línea a través de los puntos. Extiende la línea para llenar la cuadrícula y coloca flechas en ambos extremos de la línea.
Es cierto que sólo se necesitan dos puntos para determinar una línea, pero es un buen hábito usar tres puntos. Si trazas solo dos puntos y uno de ellos es incorrecto, aún puedes dibujar una línea pero no representará las soluciones a la ecuación. Será la línea equivocada. Si usas tres puntos, y uno es incorrecto, los puntos no se alinearán. Esto te dice que algo anda mal y necesitas revisar tu trabajo. Ver Figura\(\PageIndex{4}\).

Figura\(\PageIndex{4}\) - Observa la diferencia entre (a) y (b). Los tres puntos en (a) se alinean para que podamos trazar una línea a través de ellos. Los tres puntos de la (b) no se alinean. No podemos trazar una sola línea recta a través de los tres puntos.
Grafica la ecuación y = −3x.
Solución
Encuentra tres puntos que son soluciones a la ecuación. Es más fácil elegir valores para x, y resolver para y. ¿Ves por qué?

Enumere los puntos en una tabla.
| y = −3x | ||
|---|---|---|
| x | y | (x, y) |
| 0 | 0 | (0, 0) |
| 1 | -3 | (1, -3) |
| -2 | 6 | (-2, 6) |
Traza los puntos, verifica que se alineen y dibuja la línea como se muestra.

Grafica la ecuación trazando puntos: y = −4x.
- Responder

Grafica la ecuación trazando puntos: y = x.
- Responder
-

Cuando una ecuación incluye una fracción como coeficiente de x, podemos sustituir cualquier número por x. Pero la matemática es más fácil si hacemos “buenas” elecciones para los valores de x. De esta manera evitaremos respuestas de fracciones, que son difíciles de graficar con precisión.
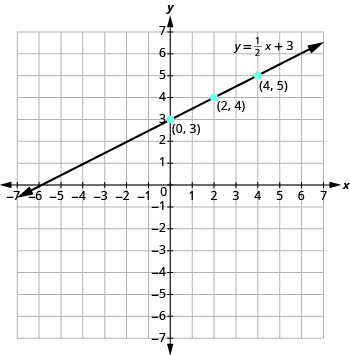
Grafica la ecuación y =\(\dfrac{1}{2}\) x + 3.
Solución
Encuentra tres puntos que son soluciones a la ecuación. Dado que esta ecuación tiene la fracción\(\dfrac{1}{2}\) como un coeficiente de x, elegiremos valores de x cuidadosamente. Usaremos cero como una opción y múltiplos de 2 para las otras opciones.

Los puntos se muestran en la tabla.
| y =\(\dfrac{1}{2}\) x + 3 | ||
|---|---|---|
| \ (\ dfrac {1} {2}\) x + 3">x | y | (x, y) |
| \ (\ dfrac {1} {2}\) x + 3">0 | 3 | (0, 3) |
| \ (\ dfrac {1} {2}\) x + 3">2 | 4 | (2, 4) |
| \ (\ dfrac {1} {2}\) x + 3">4 | 5 | (4, 5) |
Traza los puntos, verifica que se alineen y dibuja la línea como se muestra.
Graficar la ecuación: y =\(\dfrac{1}{3}\) x − 1
- Responder
-

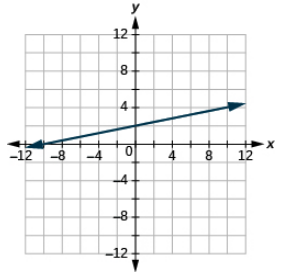
Grafica la ecuación: y =\(\dfrac{1}{4}\) x + 2.
- Responder
-
Hasta ahora, todas las ecuaciones que graficamos tenían y dadas en términos de x Ahora vamos a graficar una ecuación con x e y en el mismo lado.
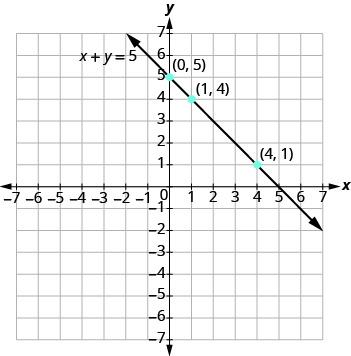
Grafica la ecuación x + y = 5.
Solución
Encuentra tres puntos que son soluciones a la ecuación. Recuerda, puedes comenzar con cualquier valor de x o y.

Enumeramos los puntos en una tabla.
| x + y = 5 | ||
|---|---|---|
| x | y | (x, y) |
| 0 | 5 | (0, 5) |
| 1 | 4 | (1, 4) |
| 4 | 1 | (4, 1) |
Después, trazar los puntos, verificar que se alineen y trazar la línea.
Grafica la ecuación: x + y = −2.
- Responder
-

Grafica la ecuación: x − y = 6.
- Responder
-

En el ejemplo anterior, los tres puntos que encontramos fueron fáciles de graficar. Pero no siempre es así. Veamos qué pasa en la ecuación 2x + y = 3. Si y es 0, ¿cuál es el valor de x?
\[\begin{split} 2x + y &= 3 \\ 2x + \textcolor{red}{0} &= 3 \\ 2x &= 3 \\ x &= \dfrac{3}{2} \end{split}\]
La solución es el punto\(\left(\dfrac{3}{2}, 0\right)\). Este punto tiene una fracción para la coordenada x. Si bien podríamos graficar este punto, es difícil ser precisos graficando fracciones. Recuerda en el ejemplo y =\(\dfrac{1}{2}\) x + 3, elegimos cuidadosamente los valores para x para no graficar fracciones en absoluto. Si resolvemos la ecuación 2x + y = 3 para y, será más fácil encontrar tres soluciones a la ecuación.
\[\begin{split} 2x + y &= 3 \\ y &= -2x + 3 \end{split}\]
Ahora podemos elegir valores para x que darán coordenadas que son enteros. Se muestran las soluciones para x = 0, x = 1 y x = −1.
| y = −2x + 3 | ||
|---|---|---|
| x | y | (x, y) |
| 0 | 3 | (0, 3) |
| 1 | 1 | (1, 1) |
| -1 | 5 | (-1, 5) |

Grafica la ecuación 3x + y = −1.
Solución
Encuentra tres puntos que son soluciones a la ecuación.
Primero, resolver la ecuación para y.
\[\begin{split} 3x + y &= −1 \\ y &= −3x − 1 \end{split}\]
Dejaremos que x sea 0, 1 y −1 para encontrar tres puntos. Los pares ordenados se muestran en la tabla. Trazar los puntos, verificar que se alineen y trazar la línea.
| y = −3x − 1 | ||
|---|---|---|
| x | y | (x, y) |
| 0 | -1 | (0, -1) |
| 1 | -4 | (1, -4) |
| -1 | 2 | (-1, 2) |

Si puedes elegir tres puntos para graficar una línea, ¿cómo sabrás si tu gráfica coincide con la que se muestra en las respuestas del libro? Si los puntos donde las gráficas cruzan los ejes x e y son los mismos, las gráficas coinciden.
Grafica cada ecuación: 2x + y = 2.
- Responder

Grafica cada ecuación: 4x + y = −3.
- Responder
-