Saltar al contenido principal
LibreTexts Español

11.E: Gráficas (Ejercicios)

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    114227

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    11.1 - Utilizar el Sistema de Coordenadas Rectangulares

    Trazar puntos en un sistema de coordenadas rectangulares

    En los siguientes ejercicios, trazar cada punto en un sistema de coordenadas rectangulares.

    1. (1, 3), (3, 1)
    2. (2, 5), (5, 2)

    En los siguientes ejercicios, trazar cada punto en un sistema de coordenadas rectangulares e identificar el cuadrante en el que se encuentra el punto.

    1. (a) (−1, −5) (b) (−3, 4) (c) (2, −3) (d)\(\left(1, \dfrac{5}{2}\right)\)
    2. (a) (3, −2) (b) (−4, −1) (c) (−5, 4) (d)\(\left(2, \dfrac{10}{3}\right)\)

    Identificar puntos en una gráfica

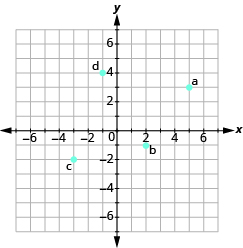
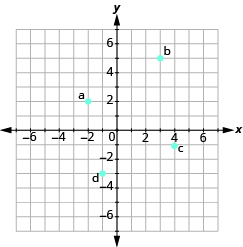
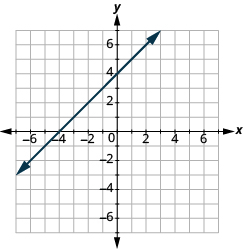
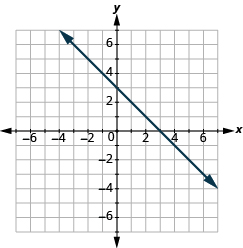
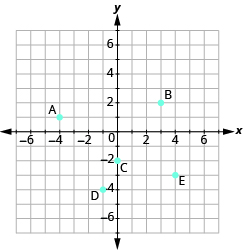
    En los siguientes ejercicios, nombra el par ordenado de cada punto que se muestra en el sistema de coordenadas rectangulares.

    1. La gráfica muestra el plano de la coordenada x y. Los ejes van de -7 a 7. “a” se traza en 5, 3, “b” en 2, -1, “c” en -3, -2 y “d” en -1,4.
    2. La gráfica muestra el plano de la coordenada x y. Los ejes van de -7 a 7. “a” se traza en -2, 2, “b” en 3, 5, “c” en 4, -1 y “d” en -1,3.
    3. La gráfica muestra el plano de la coordenada x y. Los ejes van de -7 a 7. “a” se traza en 2, 0, “b” en 0, -5, “c” en -4,0 y “d” en 0,3.
    4. La gráfica muestra el plano de la coordenada x y. Los ejes van de -7 a 7. “a” se traza en 0, 4, “b” en 5, 0, “c” en 0, -1 y “d” en -3,0.

    Verificar soluciones a una ecuación en dos variables

    En los siguientes ejercicios, encuentra los pares ordenados que son soluciones a la ecuación dada.

    1. 5x + y = 10
      1. (5, 1)
      2. (2, 0)
      3. (4, −10)
    2. y = 6x − 2
      1. (1, 4)
      2. \(\left(\dfrac{1}{3} , 0\right)\)
      3. (6, −2)

    Completar una Tabla de Soluciones a una Ecuación Lineal en Dos Variables

    En los siguientes ejercicios, complete la tabla para encontrar soluciones a cada ecuación lineal.

    1. y = 4x − 1
    x y (x, y)
    0    
    1    
    -2    
    1. y =\(− \dfrac{1}{2}\) x + 3
    x y (x, y)
    0    
    1    
    -2    
    1. x + 2y = 5
    x y (x, y)
      0  
    1    
    -1    
    1. 3x − 2 años = 6
    x y (x, y)
    0    
      0  
    -2    

    Encuentre soluciones a una ecuación lineal en dos variables

    En los siguientes ejercicios, encuentra tres soluciones para cada ecuación lineal.

    1. x + y = 3
    2. x + y = −4
    3. y = 3x + 1
    4. y = − x − 1

    11.2 - Graficar ecuaciones lineales

    Reconocer la relación entre las soluciones de una ecuación y su gráfica

    En los siguientes ejercicios, para cada par ordenado, decidir (a) si el par ordenado es una solución a la ecuación. b) si el punto está en la línea.

    1. y = − x + 4
      1. (0, 4)
      2. (−1, 3)
      3. (2, 2)
      4. (−2, 6)

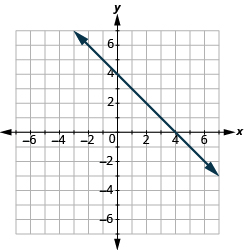
    La gráfica muestra el plano de la coordenada x y. Los ejes van de -7 a 7. Una línea pasa por los puntos “par ordenado 0, 4” y “par ordenado 4, 0”.

    1. y =\(\dfrac{2}{3}\) x − 1
      1. (0, −1)
      2. (3, 1)
      3. (−3, −3)
      4. (6, 4)

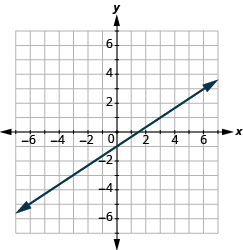
    La gráfica muestra el plano de la coordenada x y. Los ejes van de -7 a 7. Una línea pasa por los puntos “par ordenado 0, -1” y “par ordenado 3, 1”.

    Graficar una ecuación lineal trazando puntos

    En los siguientes ejercicios, grafica por puntos de trazado.

    1. y = 4x − 3
    2. y = −3x
    3. 2x + y = 7

    Gráfica líneas verticales y horizontales

    En los siguientes ejercicios, grafica las líneas verticales u horizontales.

    1. y = −2
    2. x = 3

    11.3 - Graficar con Intercepciones

    Identificar las intercepciones en una gráfica

    En los siguientes ejercicios, encuentra las intercepciones x e y.

    1. La gráfica muestra el plano de la coordenada x y. Los ejes van de -7 a 7. Una línea pasa por los puntos “par ordenado 0, 4” y “par ordenado -4, 0”.
    2. La gráfica muestra el plano de la coordenada x y. El eje x va de -1 a 6. El eje y va de -4 a 2. Una línea pasa por los puntos “par ordenado 5, 1” y “par ordenado 0, -3”.

    Encuentra las Intercepciones a partir de una Ecuación de una Línea

    En los siguientes ejercicios, encuentra las intercepciones.

    1. x + y = 5
    2. x − y = −1
    3. y =\(\dfrac{3}{4}\) x − 12
    4. y = 3x

    Graficar una línea usando las intercepciones

    En los siguientes ejercicios, grafica usando las intercepciones.

    1. −x + 3y = 3
    2. x + y = −2

    Elija el método más conveniente para graficar una línea

    En los siguientes ejercicios, identifica el método más conveniente para graficar cada línea.

    1. x = 5
    2. y = −3
    3. 2x + y = 5
    4. x − y = 2
    5. y =\(\dfrac{1}{2}\) x + 2
    6. y =\(\dfrac{3}{4}\) x − 1

    11.4 - Comprender la pendiente de una línea

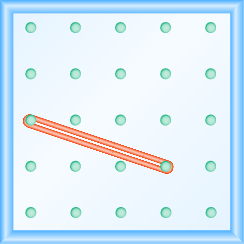
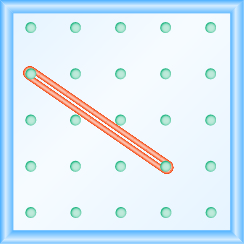
    Uso de geoplacas para modelar taludes

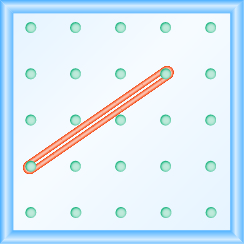
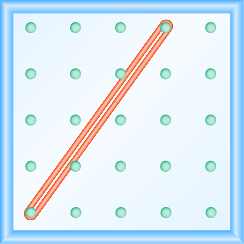
    En los siguientes ejercicios, encuentra la pendiente modelada en cada geobordo.

    1. La figura muestra una cuadrícula de puntos uniformemente espaciados. Hay 5 filas y 5 columnas. Hay un bucle estilo banda elástica que conecta el punto en la columna 1 fila 4 y el punto en la columna 4 fila 2.
    2. La figura muestra una cuadrícula de puntos uniformemente espaciados. Hay 5 filas y 5 columnas. Hay un bucle estilo banda elástica que conecta el punto en la columna 1 fila 5 y el punto en la columna 4 fila 1.
    3. La figura muestra una cuadrícula de puntos uniformemente espaciados. Hay 5 filas y 5 columnas. Hay un bucle estilo banda elástica que conecta el punto en la columna 1 fila 3 y el punto en la columna 4 fila 4.
    4. La figura muestra una cuadrícula de puntos uniformemente espaciados. Hay 5 filas y 5 columnas. Hay un bucle estilo banda elástica que conecta el punto en la columna 1 fila 2 y el punto en la columna 4 fila 4.

    En los siguientes ejercicios, modele cada pendiente. Haz un dibujo para mostrar tus resultados.

    1. \(\dfrac{1}{3}\)
    2. \(\dfrac{3}{2}\)
    3. \(− \dfrac{2}{3}\)
    4. \(− \dfrac{1}{2}\)

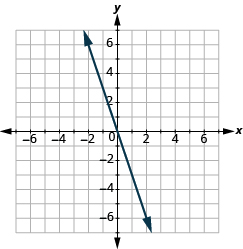
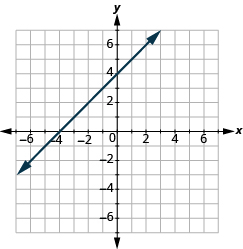
    Encuentra la Talud de una Línea a partir de su Gráfica

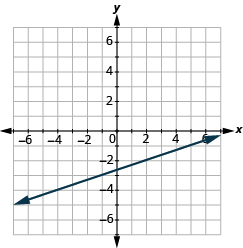
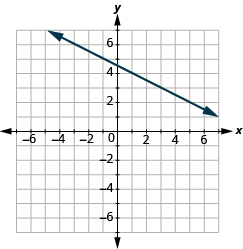
    En los siguientes ejercicios, encuentra la pendiente de cada línea mostrada.

    1. La gráfica muestra el plano de la coordenada x y. Los ejes van de -7 a 7. Una línea pasa por los puntos “par ordenado 0, 0” y “par ordenado 2, -6”.
    2. La gráfica muestra el plano de la coordenada x y. Los ejes van de -7 a 7. Una línea pasa por los puntos “par ordenado 0, 4” y “par ordenado -4, 0”.
    3. La gráfica muestra el plano de la coordenada x y. Los ejes van de -7 a 7. Una línea pasa por los puntos “par ordenado -4, -4” y “par ordenado 5, -1”.
    4. La gráfica muestra el plano de la coordenada x y. Los ejes van de -7 a 7. Una línea pasa por los puntos “par ordenado -3, 6” y “par ordenado 5, 2”.

    Encuentra la Pendiente de Líneas Horizontales y Verticales

    En los siguientes ejercicios, encuentra la pendiente de cada línea.

    1. y = 2
    2. x = 5
    3. x = −3
    4. y = −1

    Usa la Fórmula de Talud para encontrar la Talud de una Línea entre Dos Puntos

    En los siguientes ejercicios, usa la fórmula de pendiente para encontrar la pendiente de la línea entre cada par de puntos.

    1. (2, 1), (4, 5)
    2. (−1, −1), (0, −5)
    3. (3, 5), (4, −1)
    4. (−5, −2), (3, 2)

    Graficar una línea dado un punto y el talud

    En los siguientes ejercicios, grafica la línea dada un punto y la pendiente.

    1. (2, −2); m =\(\dfrac{5}{2}\)
    2. (−3, 4); m =\(− \dfrac{1}{3}\)

    Resolver aplicaciones de pendientes

    En el siguiente ejercicio, resolver la aplicación del talud.

    1. Un techo tiene una altura de 10 pies y una carrera de 15 pies. ¿Cuál es su pendiente?

    PRUEBA DE PRÁCTICA

    1. Trazar y etiquetar estos puntos:
      1. (2, 5)
      2. (−1, −3)
      3. (−4, 0)
      4. (3, −5)
      5. (−2, 1)
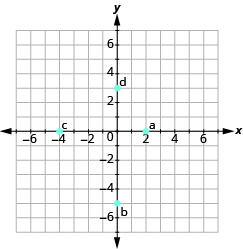
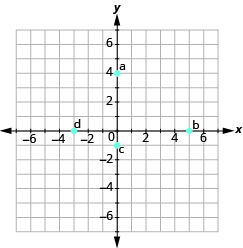
    2. Nombra el par ordenado para cada punto mostrado.

    La gráfica muestra el plano de la coordenada x y. Los ejes se extienden de -7 a 7. A se traza en -4, 1, B en 3, 2, C en 0, -2, D en -1, -4 y E en 4, -3.

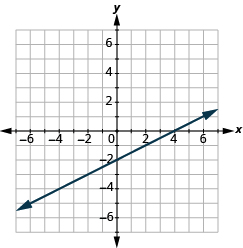
    1. Encuentra la intercepción x y la intercepción en la línea que se muestra.

    La gráfica muestra el plano de la coordenada x y. El eje x va de -7 a 7. El eje y va de -7 a 7. Una línea pasa por los puntos “par ordenado 4, 0” y “par ordenado 0, -2”.

    1. Encuentra la intercepción x y la intercepción y de la ecuación 3x − y = 6.
    2. ¿Es (1, 3) una solución a la ecuación x + 4y = 12? ¿Cómo lo sabes?
    3. Completa la tabla para encontrar cuatro soluciones a la ecuación y = − x + 1.
    x y (x, y)
    0    
    1    
    3    
    -2    
    1. Completa la tabla para encontrar tres soluciones a la ecuación 4x + y = 8.
    x y (x, y)
    0    
      0  
    3    

    En los siguientes ejercicios, encuentra tres soluciones para cada ecuación y luego grafica cada línea.

    1. y = −3x
    2. 2x + 3y = −6

    En los siguientes ejercicios, encuentra la pendiente de cada línea.

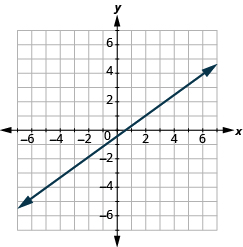
    1. La gráfica muestra el plano de la coordenada x y. Los ejes van de -7 a 7. El eje y va de -5 a -4. Una línea pasa por los puntos “par ordenado 6, 4” y “par ordenado 0, -3”.
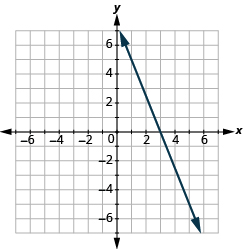
    2. La gráfica muestra el plano de la coordenada x y. Los ejes van de -7 a 7. Una línea pasa por los puntos “par ordenado 3, 0” y “par ordenado 1, 5”.
    3. Utilice la fórmula de pendiente para encontrar la pendiente de la línea entre (0, −4) y (5, 2).
    4. Encuentra la pendiente de la línea y = 2.
    5. Grafica la línea que pasa por (1, 1) con pendiente m =\(\dfrac{3}{2}\).
    6. Una ruta en bicicleta sube 20 pies para 1,000 pies de distancia horizontal. ¿Cuál es la pendiente de la ruta?

    Colaboradores y Atribuciones

    11.E: Gráficas (Ejercicios) is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.