4.2.2: Movimientos equilibrados

Lección

Reescribamos ecuaciones manteniendo las mismas soluciones.

Ejercicio$\PageIndex{1}$: Matching Hangers

Las figuras A, B, C y D muestran el resultado de simplificar el colgador en la figura A eliminando pesos iguales de cada lado.

Figura$\PageIndex{1}$: Cuatro perchas balanceadas. A. Lado izquierdo, 1 cuadrado, 3 triángulos, 1 cuadrado, 3 triángulos, 2 círculos. Lado derecho, 2 círculos, 4 cuadrados, 2 triángulos. B. Lado izquierdo, 1 cuadrado, 3 triángulos, 1 cuadrado, 3 triángulos. Lado derecho, 4 cuadrados, 2 triángulos. C. Lado izquierdo, 1 cuadrado, 3 triángulos, lado derecho, 2 cuadrados, 1 triángulo. D. Lado izquierdo, 2 triángulos. Lado derecho, 1 cuadrado.

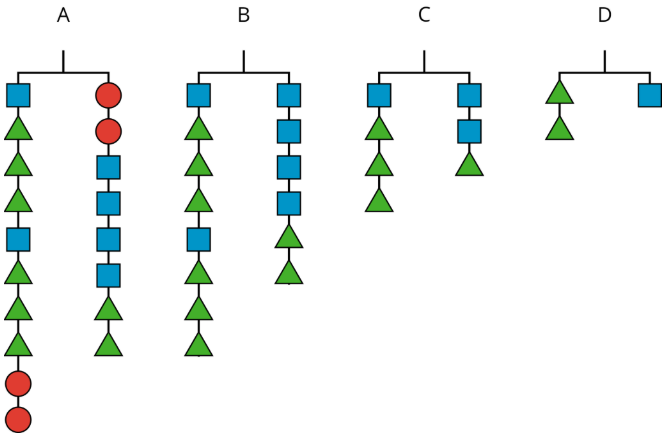
Aquí hay algunas ecuaciones. Cada ecuación representa uno de los diagramas de colgador.

$(2(x+3y)=4x+2y\qquad 2y=x\qquad 2(x+3y)+2z=2z+4x+2y\qquad x+3y=2x+y$

1. Escribe la ecuación que va con cada figura:
2. Cada variable$(x, y$, y$z)$ representa el peso de una forma. ¿Cuál va con cuál?
3. Explique qué se le hizo a cada ecuación para crear la siguiente ecuación. Si te quedas atascado, piensa en cómo cambiaron las perchas.

Ejercicio$\PageIndex{2}$: Matching Equation Moves

Tu profesor te dará algunas tarjetas. Cada una de las cartas 1 a 6 muestran dos ecuaciones. Cada una de las cartas de la A a la E describe un movimiento que convierte una ecuación en otra.

1. Haga coincidir cada tarjeta numérica con una carta.
2. Una de las cartas carta no tendrá partido. Para esta tarjeta, escriba dos ecuaciones que muestren el movimiento descrito.

Ejercicio$\PageIndex{3}$: Keeping Equality

1. Noah y Lin resolvieron la ecuación$14a=2(a-3)$.

¿Estás de acuerdo con alguno de ellos? ¿Por qué?

La solución de Noé:

$$\begin{aligned} 14a&=2(a-3)\\14a&=2a-6\\12a&=-6\\a&=-\frac{1}{2}\end{aligned}\nonumber$$

La solución de Lin:

$$\begin{aligned} 14a&=2(a-3)\\7a&=a-3\\6a&=-3\\a&=-\frac{1}{2}\end{aligned}\nonumber$$

2. Se le pide a Elena que resuelva$15-10x=5(x+9)$. ¿Qué recomiendas que le haga primero a cada lado?

3. Se le pide a Diego que suelte$3x-8=4(x+5)$. ¿Qué recomiendas que le haga primero a cada lado?

¿Estás listo para más?

En un rompecabezas criptaritmético, los dígitos 0—9 se representan con letras del alfabeto. Usa tu comprensión de la suma para encontrar qué dígitos van con las letras A, B, E, G, H, L, N y R.

PERCHA + PERCHA + PERCHA = ÁLGEBRA

Resumen

Una ecuación nos dice que dos expresiones tienen igual valor. Por ejemplo, si$4x+9$ y$-2x-3$ tienen igual valor, podemos escribir la ecuación

$4x+9=-2x-3$

Anteriormente, usamos perchas para entender que si agregamos el mismo número positivo a cada lado de la ecuación, los lados seguirán teniendo el mismo valor. ¡También funciona si sumamos números negativos! Por ejemplo, podemos sumar -9 a cada lado de la ecuación.

$$\begin{aligned} 4x+9+-9&=-2x-3+-9 &\text{add -9 to each side} \\ 4x&=-2x-12 &\text{combine like terms}\end{aligned}$$

Dado que las expresiones representan números, también podemos agregar expresiones a cada lado de una ecuación. Por ejemplo, podemos sumar$2x$ a cada lado y seguir manteniendo la igualdad.

$$\begin{aligned} 4x+2x&=-2x-12+2x &\text{add 2x to each side} \\ 6x&=-12 &\text{combine like terms}\end{aligned}$$

Si multiplicamos o dividimos las expresiones a cada lado de una ecuación por el mismo número, también mantendremos la igualdad (siempre y cuando no dividamos por cero).

$$6x\cdot\frac{1}{6}=-12\cdot\frac{1}{6}\qquad \text{multiply each side by }\frac{1}{6}\nonumber$$

o

$$6x\div 6=-12\div 6\qquad\text{divide each side by }6\nonumber$$

Ahora podemos ver que esa$x=-2$ es la solución a nuestra ecuación.

Utilizaremos estos movimientos de manera sistemática para resolver ecuaciones en lecciones futuras.

Practica

Ejercicio$\PageIndex{4}$

En esta percha, el peso del triángulo es$x$ y el peso del cuadrado es$y$.

Figura$\PageIndex{2}$

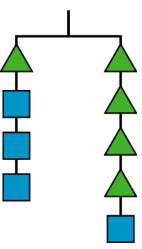
1. Escribe una ecuación usando$x$ y$y$ para representar el colgador.
2. Si$x$ es 6, ¿qué es$y$?

Ejercicio$\PageIndex{5}$

Andre y Diego intentaban resolver cada uno$2x+6=3x-8$. Describir el primer paso que cada uno hace a la ecuación.

1. El resultado del primer paso de Andre fue$-x+6=-8$.
2. El resultado del primer paso de Diego fue$6=x-8$.

Ejercicio$\PageIndex{6}$

1. Complete la tabla con valores para$x$ o$y$ que hagan verdadera esta ecuación:$3x+y=15$.

   Mesa$\PageIndex{1}$

   $x$	2		6	0	3
   $y$		3				0	8

2. Crea una gráfica, traza estos puntos y encuentra la pendiente de la línea que los atraviesa.

Figura$\PageIndex{3}$

(De la Unidad 3.3.3)

Ejercicio$\PageIndex{7}$

Empareja cada conjunto de ecuaciones con el movimiento que convirtió la primera ecuación en la segunda.

1. $$\begin{aligned} 6x+9&=4x-3 \\ 2x+9&=-3\end{aligned}\nonumber$$
2. $$\begin{aligned} -4(5x-7)&=-18 \\5x-7&=4.5\end{aligned}\nonumber$$
3. $$\begin{aligned} 8-10x&=7+5x\\4-10x&=3+5x\end{aligned}\nonumber$$
4. $$\begin{aligned} \frac{-5x}{4}&=4\\5x&=-16\end{aligned}\nonumber$$
5. $$\begin{aligned} 12x+4&=20x+24 \\ 3x+1&=6x+6\end{aligned}\nonumber$$

1. Multiplicar ambos lados por$\frac{-1}{4}$
2. Multiplicar ambos lados por$-4$
3. Multiplicar ambos lados por$\frac{1}{4}$
4. Agregar$-4x$ a ambos lados
5. Agregar$-4$ a ambos lados

Ejercicio$\PageIndex{8}$

Seleccione todas las situaciones para las que solo tengan sentido soluciones cero o positivas.

1. Medir la temperatura en grados Celsius en un puesto avanzado ártico cada día en enero.
2. La altura de una vela ya que se quema más de una hora.
3. La elevación sobre el nivel del mar de un excursionista que desciende a un cañón.
4. El número de alumnos que permanecen en la escuela después de las 6:00 p.m.
5. Un saldo de cuenta bancaria a lo largo de un año.
6. La temperatura en grados Fahrenheit de un horno utilizado en un caluroso día de verano.

(De la Unidad 3.5.1)