4.2.3: Movimientos más equilibrados

Última actualización

30 oct 2022
Guardar como PDF
- 4.2.2: Movimientos equilibrados
- 4.2.4: Resolver cualquier ecuación lineal

Illustrative Mathematics
OpenUp Resources

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Lección

Reescribamos algunas ecuaciones más manteniendo las mismas soluciones.

Ejercicio $\PageIndex{1}$ : Different Equations?

Ecuación 1

$x-3=2-4x\nonumber$

¿Cuáles de estos tienen la misma solución que la Ecuación 1? Esté preparado para explicar su razonamiento.

$\begin{array}{ccccccc}{\text{Equation A}}&{\quad}&{\text{Equation B}}&{\quad}&{\text{Equation C}}&{\quad}&{\text{Equation D}}\\{2x-6=4-8x}&{\quad}&{x-5=-4x}&{\quad}&{2(1-2x)=x-3}&{\quad}&{-3=2-5x}\end{array}\nonumber$

Ejercicio $\PageIndex{2}$ : Step by Step by Step by Step

Aquí hay una ecuación, y luego todos los pasos que escribió Clare para resolverla:

$\begin{aligned}14x-2x+3&=3(5x+9) \\ 12x+3&=3(5x+9) \\ 3(4x+1)&=3(5x+9) \\ 4x+1&=5x+9 \\ 1&=x+9 \\ -8&=x \end{aligned}\nonumber$

Aquí está la misma ecuación, y los pasos que Lin escribió para resolverla:

$\begin{aligned} 14x-2x+3&=3(5x+9) \\ 12x+3&=3(5x+9) \\ 12x+3&=15x+27 \\ 12x&=15x+24 \\ -3x&=24 \\ x&=-8\end{aligned}\nonumber$

¿Ambas soluciones son correctas? Explica tu razonamiento.
Describir algunas formas en que los pasos que tomaron son iguales y diferentes.
Mai y Noah también resolvieron la ecuación, pero algunos de sus pasos tienen errores. Encuentra el paso incorrecto en cada solución y explica por qué es incorrecto.

Mai:

$\begin{aligned} 14x-2x+3&=3(5x+9) \\ 12x+3&-3(5x+9) \\ 7x+3&=3(9) \\ 7x+3&=27 \\ 7x&=24 \\ x&=\frac{24}{7}\end{aligned}\nonumber$

Noé:

$\begin{aligned} 14x-2x+3&=3(5x+9) \\ 12x+3&=15x+27 \\ 27x+3&=27 \\ 27x&=24 \\ x&=\frac{24}{27}\end{aligned}\nonumber$

Ejercicio $\PageIndex{3}$ : Make Your Own Steps

Resuelve estas ecuaciones para $x$ .

$\frac{12+6x}{3}=\frac{5-9}{2}$
$x-4=\frac{1}{3}(6x-54)$
$-(3x-12)=9x-4$

¿Estás listo para más?

Tengo 24 lápices y 3 tazas. La segunda copa sostiene un lápiz más que el primero. El tercero tiene uno más que el segundo. ¿Cuántos lápices contiene cada taza?

Resumen

¿Cómo nos aseguramos de que la solución que encontramos para una ecuación sea correcta? Sumando accidentalmente cuando queríamos restar, perder un negativo cuando distribuimos, olvidando escribir una $x$ de una línea a la siguiente, ¡hay muchos errores posibles a tener en cuenta!

Afortunadamente, cada paso que damos resolviendo una ecuación da como resultado una nueva ecuación con la misma solución que la original. Esto significa que podemos verificar nuestro trabajo sustituyendo el valor de la solución en la ecuación original. Por ejemplo, digamos que resolvemos la siguiente ecuación:

$\begin{aligned} 2x&=-3(x+5) \\ 2x&=-3x+15 \\ 5x&=15 \\ x&=3\end{aligned}\nonumber$

Sustituyendo 3 en lugar de $x$ en la ecuación original,

$\begin{aligned} 2(3)&=-3(3+5) \\ 6&=-3(8) \\ 6&=-24\end{aligned}\nonumber$

¡obtenemos una declaración que no es verdad! Esto nos dice que debemos haber cometido un error en alguna parte. Comprobando cuidadosamente nuestros pasos originales, cometimos un error al distribuir -3. Fijándolo, ahora tenemos

$\begin{aligned} 2x&=-3(x+5) \\ 2x&=-3x-15 \\ 5x&=-15 \\ x&=-3\end{aligned}\nonumber$

Sustituyendo -3 en lugar de $x$ en la ecuación original para asegurarnos de que no cometimos otro error:

$\begin{aligned} 2(-3)&=-3(-3+5) \\ -6&=-3(2) \\ -6&=-6\end{aligned}\nonumber$

Esta ecuación es cierta, también lo $x=-3$ es la solución.

Practica

Ejercicio $\PageIndex{4}$

Mai y Tyler trabajan $\frac{2}{5}b+1=-11$ juntos en la ecuación. La solución de Mai es $b=-25$ y la de Tyler es $b=-28$ . Aquí está su trabajo. ¿Estás de acuerdo con sus soluciones? Explica o muestra tu razonamiento.

Mai:

$\begin{aligned} \frac{2}{5}b+1&=-11 \\ \frac{2}{5}b&=-10 \\ b&=-10\cdot\frac{5}{2} \\ b&=-25\end{aligned}\nonumber$

Tyler:

$\begin{aligned} \frac{2}{5}b+1&=-11 \\ 2b+1&=-55 \\ 2b&=-56 \\ b&=-28\end{aligned}\nonumber$

Ejercicio $\PageIndex{5}$

Resolver $3(x-4)=12x$

Ejercicio $\PageIndex{6}$

Describir lo que se está haciendo en cada paso mientras se resuelve la ecuación.

$2(-3x+4)=5x+2$
$-6x+8=5x+2$
$8=11x+2$
$6=11x$
$x=\frac{6}{11}$

Ejercicio $\PageIndex{7}$

Andre resolvió una ecuación, pero cuando comprobó su respuesta vio que su solución era incorrecta. Sabe que cometió un error, pero no lo encuentra. ¿Dónde está el error de Andre y cuál es la solución a la ecuación?

$\begin{aligned} -2(3x-5)&=4(x+3)+8 \\ -6x+10&=4x+12+8 \\ -6x+10&=4x+20 \\ 10&=-2x+20 \\ -10&=-2x \\ 5&=x\end{aligned}\nonumber$

Ejercicio $\PageIndex{8}$

Elija la ecuación que tenga soluciones $(5,7)$ y $(8,13)$ .

$3x-y=8$
$y=x+2$
$y-x=5$
$y=2x-3$

(De la Unidad 3.4.1)

Ejercicio $\PageIndex{9}$

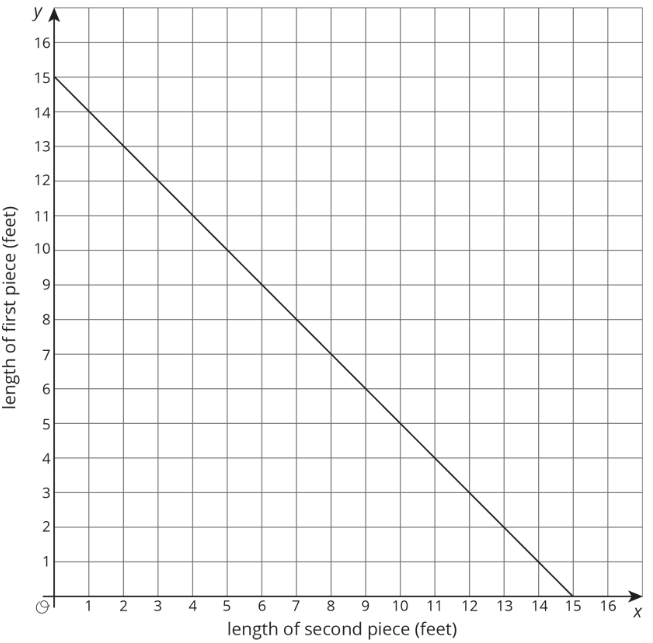
Una longitud de cinta se corta en dos piezas para usar en un proyecto de manualidades. La gráfica muestra la longitud de la segunda pieza, $x$ , para cada longitud de la primera pieza, $y$ .

¿Cuánto dura la cinta? Explica cómo sabes.
¿Cuál es la pendiente de la línea?
Explique qué representa la pendiente de la línea y por qué se ajusta a la historia.

Figura $\PageIndex{1}$ : La gráfica de una línea en el plano x y, origen O, con cuadrícula. Eje horizontal, longitud de la segunda pieza en pies, escala de 0 a 16, por 1's, Eje vertical, longitud de la primera pieza en pies, escala de 0 a 16, por 1s. La línea cruza el eje y en 15 y el eje x en 15.

(De la Unidad 3.3.1)

Search

Text Color

Text Size

Margin Size

Font Type

Lección

Resumen

Practica

Support Center

How can we help?