4.4: Ecuaciones de Valor Absoluto y Desigualdades Aplicadas a la Distancia

Última actualización
Guardar como PDF

Page ID: 115848

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La función de valor absoluto, denotada$y=|x|$, toma cualquier entrada negativa de número real y emite la versión positiva de ese número. Los números no negativos se dejan sin cambios. Aquí hay algunos ejemplos:

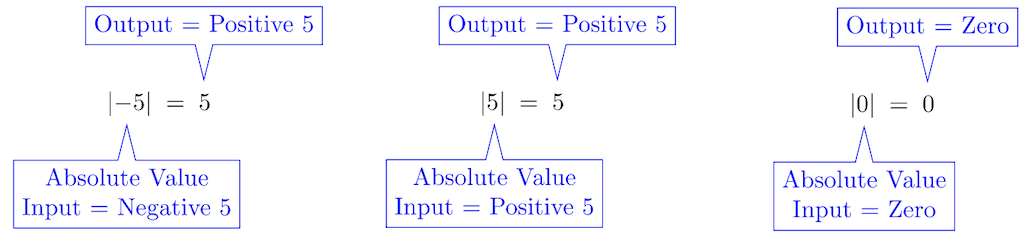
$clipboard_e6c7e1a344033657c2988c6a555298bc2.png$

La medición de la distancia es una buena aplicación para demostrar la utilidad de esta función. La distancia nunca es negativa. De hecho, veamos la función de valor absoluto a través de la lente de medir la distancia para comprender mejor las ecuaciones y desigualdades de valores absolutos:

Definición geométrica del valor absoluto de un número real

El valor absoluto de un número real$b$, denotado$|b|$, es la distancia entre cero y$b$ en la recta numérica.

Los ejemplos anteriores pueden ser interpretados geométricamente por esta gráfica:

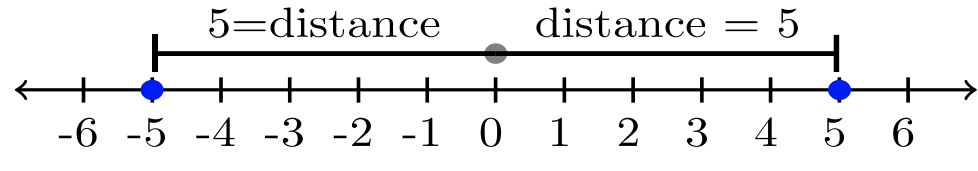
$clipboard_e860d48e41f585c8daf81ed3862fd3345.png$

Ejemplo 4.4.1

Resolver para$x$:$|x| = 3$.

Solución

¿Qué números son una distancia de$3$ unidades de cero? ¡Un gráfico de líneas numéricos nos dice! Ambos$3$ y$-3$ están a una distancia de$3$ unidades de cero.

Responder$x = \{−3, 3\}$

La distancia entre a y b

El valor absoluto se usa a menudo para medir la distancia entre dos números,$a$ y$b$. Si usamos barras de valor absoluto alrededor de la cantidad restada, entonces el orden de resta no importa.

Distancia de a a b

La distancia de$a$ a$b$ es el valor absoluto de la diferencia.

$|a-b| = |b-a| = \text{distance between } a \text{ and } b$

Dibuja una recta numérica y practica encontrar la distancia entre dos puntos cualesquiera. ¡Convéncete de que la fórmula anterior funciona!

Ejemplo 4.4.2

Resolver para$x$:$|x-3| = 4$

Utilice el concepto geométrico de distancia para mostrar solución.

Solución

Vamos a dividir la ecuación en palabras significativas:

$\overbrace{|x-3|}^{\text{distance from } x \text{ to } 3} \overbrace{=}^{\text{is}} 4: “\text{The distance from the number \(3$a otro número$x$ es$4$ unidades.}”\)

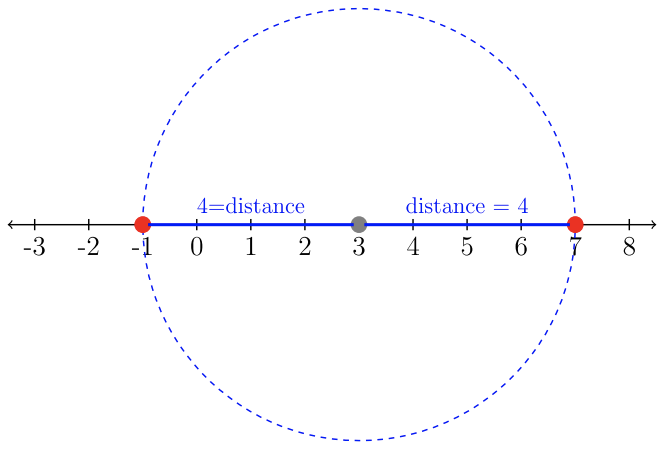
$clipboard_e4f1a30adcc425e61e0b304401792dca8.png$

Es bastante efectivo pensar en el valor$3$ como el centro de un círculo de radio$4$. El círculo cruza la recta numérica, marcando la distancia de$4$ las unidades en cada dirección. El visual nos dice que las dos respuestas son$−1$ y$7$.

Responder$x = \{−1, 7\}$

$\textcolor{green}{\checkmark}$Confirme que la solución visual coincide con la matemática:

$\begin{array} &\text{Let } x = −1 &&\;\;\;\;\;\;\;\;\;\;\;\;\;\text{Let } x = 7 \\ |x-3| &=4 &\;\;\;\;\;\;\;\;\;\;\;\;\;|x-3| &=4 \\ |-1-3| &\stackrel{?}{=} 4 &\;\;\;\;\;\;\;\;\;\;\;\;\; |7-3| &\stackrel{?}{=} 4 \\ |-4| &\stackrel{?}{=} 4 &\;\;\;\;\;\;\;\;\;\;\;\;\; |4| &\stackrel{?}{=} 4 \\ 4&=4 \;\; \checkmark &\;\;\;\;\;\;\;\;\;\;\;\;\; 4&=4 \;\; \checkmark \end{array}$

Desigualdades de valor absoluto

Ahora que tienes el truco de resolver ecuaciones de valor absoluto que describen una distancia, sigamos usando la recta numérica para resolver las desigualdades de valor absoluto. Colocar un círculo cuyo radio sea la distancia dada y el centro sea un valor dado en la ecuación o desigualdad. ¡La respuesta te saltará visualmente!

Ejemplo 4.4.3

Resolver para$x$:$|x-3| < 4$

Solución

Compare esta desigualdad con la ecuación en Ejemplo$4.4.2$.

Comencemos la solución de manera similar: hacer una frase significativa de la desigualdad.

“La distancia del número$3$ a un número$x$ es menor que$4$ las unidades”.

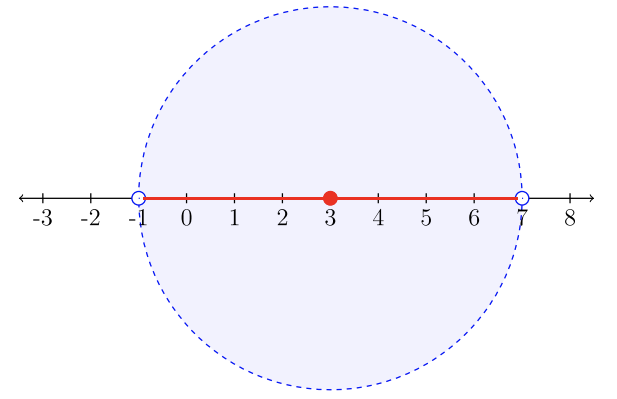
$clipboard_e161e2f11fed83382a13f4c0299c206e6.png$

El conjunto de soluciones serán todos los números a una distancia de$4$ las unidades del número$3$. El círculo marca el límite de nuestra desigualdad. El conjunto de soluciones son los números dentro del límite. Esta vez, la solución es un intervalo, describiendo todos los números reales entre$−1$ y$7$,$−1$ sin incluir ni$7$.

Conjunto de soluciones:$\{x| − 1 < x < 7\}$ o el intervalo$(−1, 7)$.

Ejemplo 4.4.4

Resolver para$t$:$|t-3| > 4$

Solución

Comparar esta desigualdad con la desigualdad en Ejemplo$4.4.3$.

Nuevamente, se utiliza la aplicación significativa de la distancia para encontrar la solución visualmente.

“La distancia del número$3$ a otro número$t$ es mayor que$4$ las unidades”.

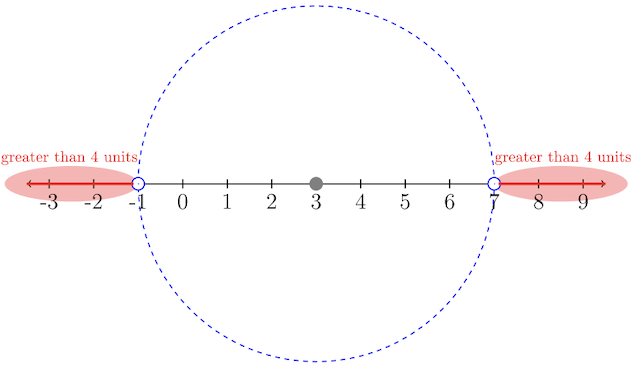
$clipboard_e01d5155bdb151958731963d1d69934e3.png$

El conjunto de soluciones será todos los números más allá de una distancia de$4$ unidades del número$3$. El círculo marca el límite de nuestra desigualdad. El conjunto de soluciones son los números fuera del límite del círculo. El conjunto de soluciones es una desigualdad compuesta ya que los números excluidos del conjunto de soluciones están dentro del límite del círculo.

Conjunto de soluciones:$\{t| t < −1 \text{ or } t > 7\}$

Notación de intervalos:$(−∞, −1) ∪ (7, ∞)$

Ejemplo 4.4.5

Resolver para$y$:$|y+2| \leq 5$

Solución

Si vamos a usar la distancia para encontrar una solución, nuestra desigualdad debe convertirse al valor absoluto de una diferencia.

Utilizaremos la siguiente propiedad de aritmética para convertir a diferencia:

$A + B = A - (-B)$

Por lo tanto:

$y+2 = y- (-2)$

Repasamos la desigualdad declarada:

$|y − (−2)| ≤ 5$

En palabras,

“La distancia de$-2$ a otro número$y$ es menor o igual a$5$ unidades”.

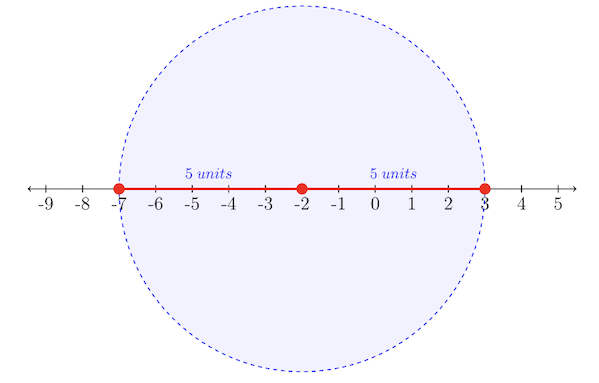
$clipboard_e6617c4077c6d367d3c5292c780e83d94.png$

El conjunto de soluciones será todos los números a una distancia de$5$ las unidades$−2$, incluyendo los valores exactamente a partir de$5$ unidades$−2$. La solución visual nos lleva a nuestra respuesta:

Conjunto de soluciones:$\{y| − 7 ≤ y ≤ 3\}$

Notación de intervalos:$[−7, 3]$

¡Pruébalo! (Ejercicios)

Para cada uno de los ejercicios #1 -23,

Interpretar la ecuación o desigualdad como distancia, usando una oración.
Resolver la desigualdad para la variable indicada, utilizando la distancia.
Exprese el conjunto de soluciones tanto en notación set-builder como en notación de intervalos.

$|x| = 6$
$|y| = 1$
$|b| = 3.26$
$|x| < 5$
$|y| > 4$
$|c| ≤ \dfrac{3}{4}$
$|q| ≥ 10.45$
$|p − 1| ≤ 2$
$|u − 2| > 3$
$|t − 4| ≤ 1$
$|x − 6.3| ≥ 4$
$|y − 3| < \dfrac{3}{2}$
$|h − 5| > \dfrac{3}{2}$
$\left|q − \dfrac{7}{2} \right| ≥ \dfrac{1}{2}$
$|w − 7| < 2.3$
$|r − 10| ≥ 0.15$
$|d − \pi| ≤ 2 \pi$
$|p − 2\pi| > \pi$
$\left|u − \dfrac{\pi}{2} \right| < \dfrac{\pi}{2}$
$|t + 4| ≤ 2$
$|x + 5| > 3$
$|r + 3| ≥ \dfrac{1}{4}$
$\left|a + \dfrac{1}{2} \right| <\dfrac{5}{2}$