3.4: Teorema de Factores y Teorema del Resto

Última actualización
Guardar como PDF

Page ID: 116446

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En la última sección, nos limitamos a encontrar las intercepciones, o ceros, de polinomios que factorizaron simplemente, o recurrimos a la tecnología. En esta sección, veremos técnicas algebraicas para encontrar los ceros de polinomios como$h(t)=t^{3} +4t^{2} +t-6$.

División Larga

En la última sección vimos que podíamos escribir un polinomio como producto de factores, cada uno correspondiente a una intercepción horizontal. Si supiéramos que$x = 2$ era una intercepción del polinomio$x^3 + 4x^2 - 5x - 14$, podríamos adivinar que el polinomio podría factorizarse como$x^{3} +4x^{2} -5x-14=(x-2)$ (algo). Para encontrar ese “algo”, podemos usar la división polinómica.

Ejemplo$\PageIndex{1}$

Dividir$x^{3} +4x^{2} -5x-14$ por$x-2$.

Solución

Comience por escribir el problema en forma de división larga

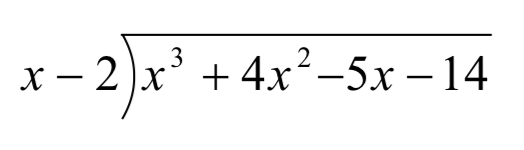
$2019-06-23 5.41.34.png$

Ahora dividimos los términos principales:$x^{3} \div x=x^{2}$. Lo mejor es alinearlo por encima del término del mismo poder en el dividendo. Ahora, multiplica eso$x^{2}$ por$x-2$ y escribe el resultado por debajo del dividendo.

$2019-06-23 5.42.53.png$

Nuevamente, dividir el término principal del resto por el término principal del divisor. $6x^{2} \div x=6x$. Sumamos esto al resultado, multiplicamos 6 x por$x-2$, y restamos.

$2019-06-23 5.43.34.png$

Esto nos dice$x^{3} +4x^{2} -5x-14$ dividido por$x-2$ es$x^{2} +6x+7$, con un resto de cero. Esto también significa que podemos factorizar$x^{3} +4x^{2} -5x-14$ como$\left(x-2\right)\left(x^{2} +6x+7\right)$.

Esto nos da una manera de encontrar las intercepciones de este polinomio.

Ejemplo$\PageIndex{2}$

Encuentra las intercepciones horizontales de$h(x)=x^{3} +4x^{2} -5x-14$.

Solución

Para encontrar las intercepciones horizontales, tenemos que resolver$h(x) = 0$. A partir del ejemplo anterior, sabemos que la función se puede factorizar como$h(x)=\left(x-2\right)\left(x^{2} +6x+7\right)$.

$h(x)=\left(x-2\right)\left(x^{2} +6x+7\right)=0$cuándo$x = 2$ o cuándo$x^{2} +6x+7=0$. Esto no factoriza muy bien, pero podríamos usar la fórmula cuadrática para encontrar los dos ceros restantes.

\[x=\dfrac{-6\pm \sqrt{6^{2} -4(1)(7)} }{2(1)} =-3\pm \sqrt{2} \nonumber \]

Las intercepciones horizontales serán en$(2,0)$,$\left(-3-\sqrt{2} ,0\right)$, y$\left(-3+\sqrt{2} ,0\right)$.

Ejercicio$\PageIndex{1}$

Dividir$2x^{3} -7x+3$$x+3$ usando división larga.

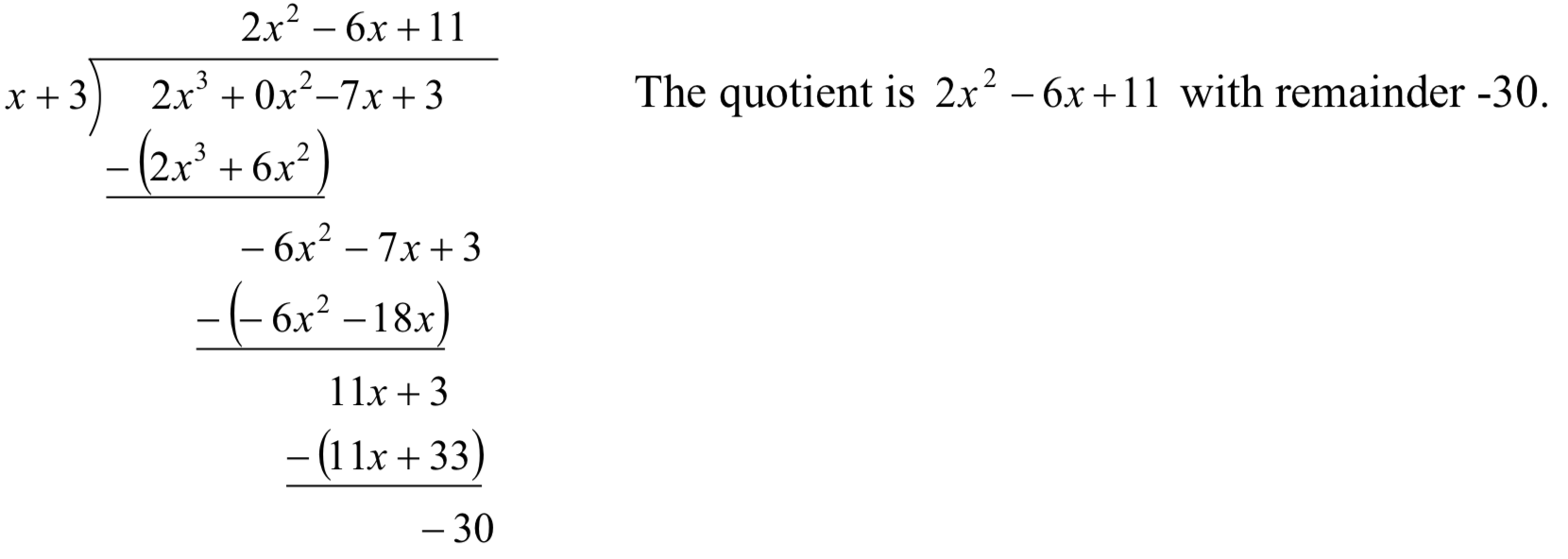
Contestar: $2019-06-23 6.07.45.png$

Los teoremas del factor y del resto

Cuando dividimos un polinomio,$p(x)$ por algún polinomio divisor$d(x)$, obtendremos un polinomio cociente$q(x)$ y posiblemente un resto$r(x)$. En otras palabras,

\[p(x)=d(x)q(x)+r(x)\]

Debido a la división, el resto será cero, o un polinomio de menor grado que d (x). Debido a esto, si dividimos un polinomio por un término de la forma$x-c$, entonces el resto será cero o una constante.

Si$p(x)=(x-c)q(x)+r$, entonces$p(c)=(c-c)q(c)+r=0+r=r$, que establece el Teorema del Resto.

El teorema del resto

Si$p(x)$ es un polinomio de grado 1 o mayor y c es un número real, entonces cuando p (x) se divide por$x-c$, el resto es$p(c)$.

Si$x-c$ es un factor del polinomio$p$, entonces$p(x)=(x-c)q(x)$ para algún polinomio$q$. Entonces$p(c)=(c-c)q(c)=0$, mostrar$c$ es un cero del polinomio. Esto no debería sorprendernos -ya sabíamos que si los factores polinomiales revela las raíces.

Si$p(c)=0$, entonces el teorema del resto nos dice que si p se divide por$x-c$, entonces el resto será cero, lo que significa que$x-c$ es un factor de$p$.

el teorema del factor

Si$p(x)$ es un polinomio distinto de cero, entonces el número real$c$ es un cero de$p(x)$ si y solo si$x-c$ es un factor de$p(x)$.

División Sintética

Dado que dividir por$x-c$ es una forma de verificar si un número es un cero del polinomio, sería bueno tener una forma más rápida de dividir por$x-c$ que tener que usar división larga cada vez. Felizmente, se han descubierto formas más rápidas.

Echemos un vistazo a la división larga que hicimos en el Ejemplo 1 e intentemos racionalizarla. Primero, cambiemos todas las restaciones en adiciones distribuyéndolas a través de los negativos.

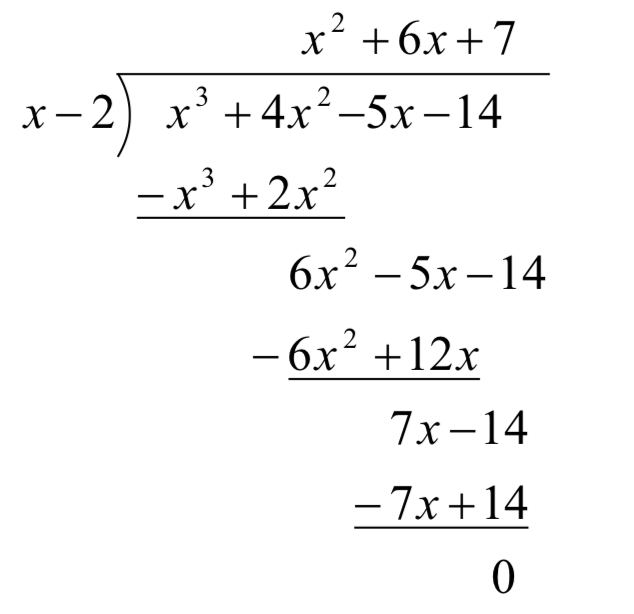
$2019-06-23 5.51.23.png$

A continuación, observar que los términos$-x^{3}$,$-6x^{2}$, y$-7x$ son exactamente lo contrario de los términos por encima de ellos. El algoritmo que utilizamos asegura que este sea siempre el caso, por lo que podemos omitirlos sin perder ninguna información. También tenga en cuenta que los términos que 'derribar' (es decir, los$\mathrm{-}$ 5x y$\mathrm{-}$ 14) no son realmente necesarios para volver a copiar, así que los omitimos, también.

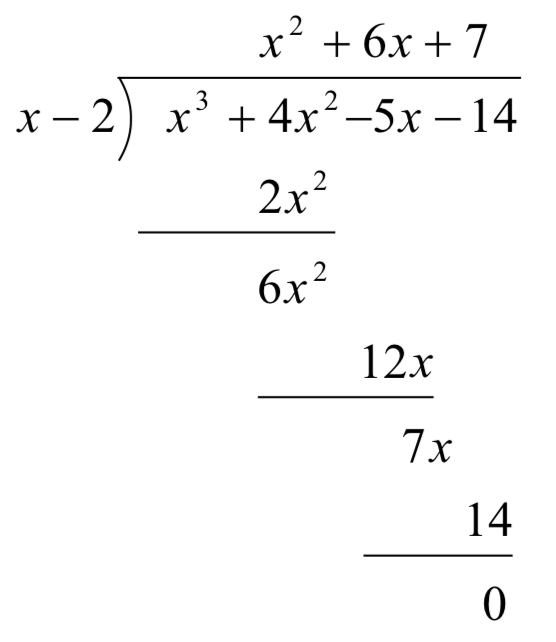
$2019-06-23 5.51.55.png$

Ahora, vamos a subir un poco las cosas y, por razones que quedarán claras en un momento, copiemos el$x^{3}$ en la última fila.

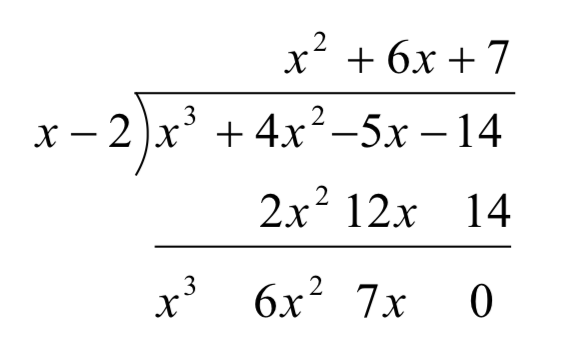
$2019-06-23 5.52.19.png$

Obsérvese que al organizar las cosas de esta manera, cada término en la última fila se obtiene sumando los dos términos por encima de él. Observe también que el polinomio cociente se puede obtener dividiendo cada uno de los tres primeros términos de la última fila por$x$ y sumando los resultados. Si te tomas el tiempo para trabajar de nuevo a través del problema de división original, encontrarás que esta es exactamente la forma en que determinamos el polinomio cociente.

Esto significa que ya no necesitamos anotar el polinomio cociente, ni el$x$ en el divisor, para determinar nuestra respuesta.

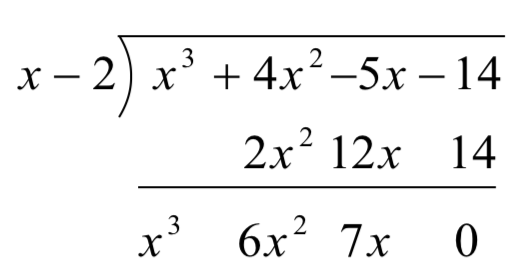
$2019-06-23 5.52.46.png$

Hemos simplificado bastante las cosas hasta ahora, pero aún podemos hacer más. Tomemos un momento para recordarnos de dónde vino el$2x^{2}$,$12x$ y 14 en la segunda fila. Cada uno de estos términos se obtuvo multiplicando los términos en el cociente,$x^{2}$, 6x y 7, respectivamente, por el -2 in$x - 2$, luego por -1 cuando cambiamos la resta a suma. Multiplicar por -2 entonces por -1 es lo mismo que multiplicar por 2, por lo que reemplazamos el -2 en el divisor por 2. Además, los coeficientes del polinomio cociente coinciden con los coeficientes de los tres primeros términos de la última fila, por lo que ahora damos el paso y escribimos solo los coeficientes de los términos para obtener

Hemos construido un cuadro de división sintética para este problema de división polinómica. Reformulemos nuestro problema de división usando este cuadro para ver cómo agiliza enormemente el proceso de división. Para dividir$x^{3} +4x^{2} -5x-14$ por$x-2$, escribimos 2 en el lugar del divisor y los coeficientes de$x^{3} +4x^{2} -5x-14$ in para el dividendo. Después “derribar” el primer coeficiente del dividendo.

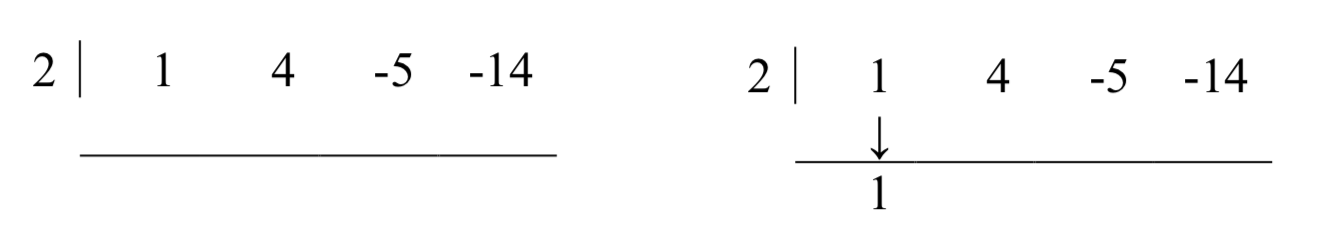
$2019-06-23 5.55.20.png$

A continuación, toma el 2 del divisor y multiplica por el 1 que fue “derribado” para obtener 2. Escribe esto debajo del 4, luego agrega para obtener 6.

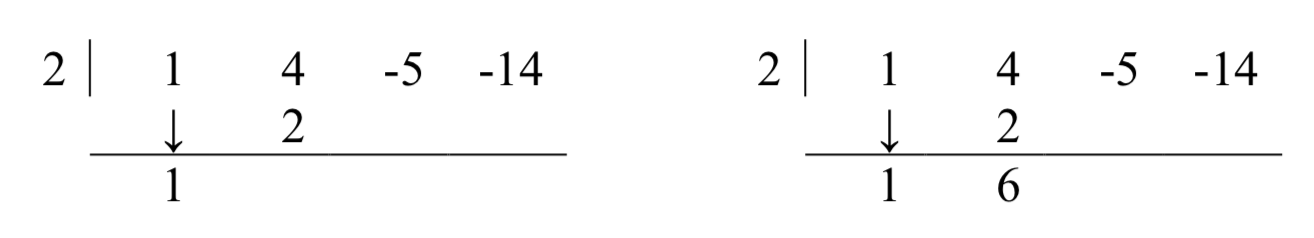
$2019-06-23 5.58.18.png$

Ahora toma el 2 del divisor por el 6 para obtener 12, y agrégalo al -5 para obtener 7.

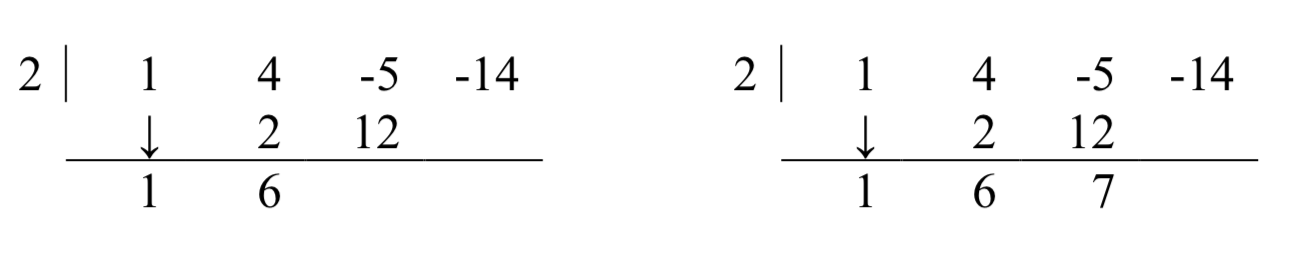
$2019-06-23 5.59.04.png$

Por último, toma el 2 en el divisor por el 7 para obtener 14, y agrégalo al -14 para obtener 0.

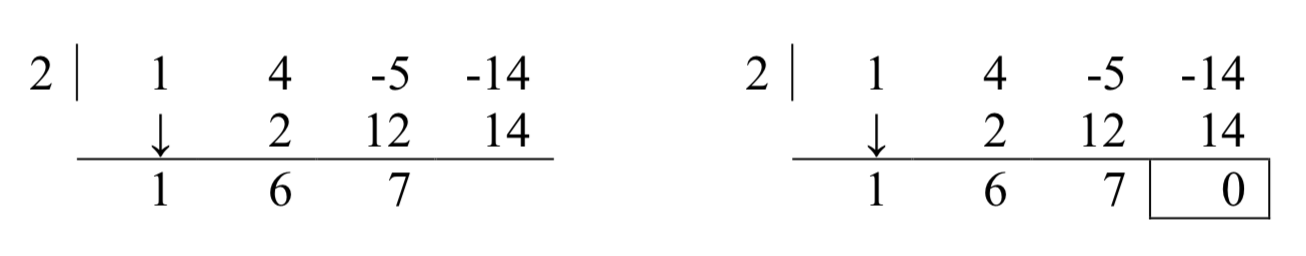
$2019-06-23 5.59.43.png$

Los tres primeros números de la última fila de nuestro cuadro son los coeficientes del polinomio cociente. Recuerde, comenzamos con un polinomio de tercer grado y dividido por un polinomio de primer grado, por lo que el cociente es un polinomio de segundo grado. De ahí que el cociente sea$x^{2} +6x+7$. El número en la casilla es el resto. La división sintética es nuestra herramienta de elección para dividir polinomios por divisores de la forma$x - c$. Es importante señalar que solo funciona para este tipo de divisores. También toma nota que cuando un polinomio (de grado al menos 1) se divide por$x - c$, el resultado será un polinomio de exactamente un grado menos. Por último, vale la pena el tiempo para rastrear cada paso en división sintética hasta su paso correspondiente en división larga.

Ejemplo$\PageIndex{3}$

Usa división sintética para dividir$5x^{3} -2x^{2} +1$ por$x-3$.

Solución

Al configurar el cuadro de división sintética, necesitamos ingresar 0 para el coeficiente de$x$ en el dividendo. Hacerlo da

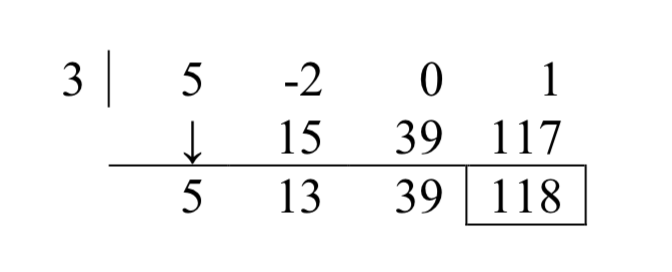
$2019-06-23 6.01.07.png$

Dado que el dividendo era un polinomio de tercer grado, el cociente es un polinomio cuadrático con coeficientes 5, 13 y 39. Nuestro cociente es$q(x)=5x^{2} +13x+39$ y el resto lo es$r(x) = 118$. Esto significa

\[5x^{3} -2x^{2} +1=(x-3)(5x^{2} +13x+39)+118\nonumber \]

También significa que no$x-3$ es un factor de$5x^{3} -2x^{2} +1$.

Ejemplo$\PageIndex{4}$

Dividir$x^{3} +8$ por$x+2$.

Solución

Para esta división, reescribimos$x+2$ como$x-\left(-2\right)$ y procedemos como antes.

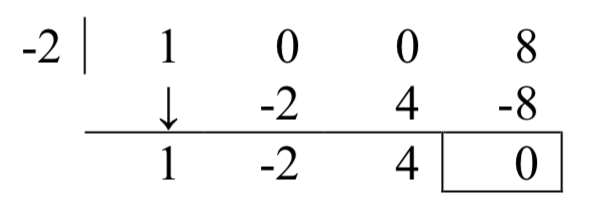
$2019-06-23 6.02.55.png$

El cociente es$x^{2} -2x+4$ y el resto es cero. Dado que el resto es cero,$x+2$ es un factor de$x^{3} +8$.

\[x^{3} +8=(x+2)\left(x^{2} -2x+4\right)\nonumber \]

Ejercicio$\PageIndex{2}$

Dividir$4x^{4} -8x^{2} -5x$ mediante$x-3$ el uso de división sintética.

Contestar

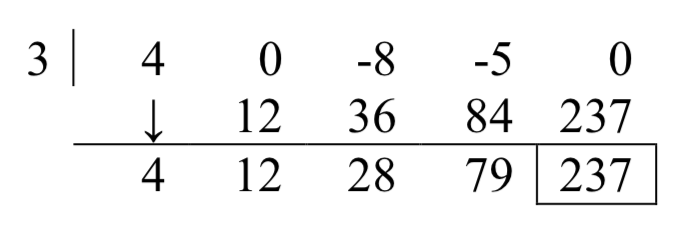
$2019-06-23 6.06.29.png$

$4x^4 - 8x^2 - 5x$dividido por$x -3$ es$4x^3 + 12x^2 + 28x + 79$ con resto 237

El uso de este proceso nos permite encontrar los ceros reales de los polinomios, presumiendo que podemos averiguar al menos una raíz. Exploraremos cómo hacerlo en la siguiente sección.

Ejemplo$\PageIndex{5}$

El polinomio$p(x)=4x^{4} -4x^{3} -11x^{2} +12x-3$ tiene una intercepción horizontal en$x=\dfrac{1}{2}$ con multiplicidad 2. Encuentra las otras intercepciones de$p(x)$.

Solución

Ya que$x=\dfrac{1}{2}$ es una intercepción con multiplicidad 2, entonces$x-\dfrac{1}{2}$ es un factor dos veces. Usa división sintética para dividir por$x-\dfrac{1}{2}$ dos veces.

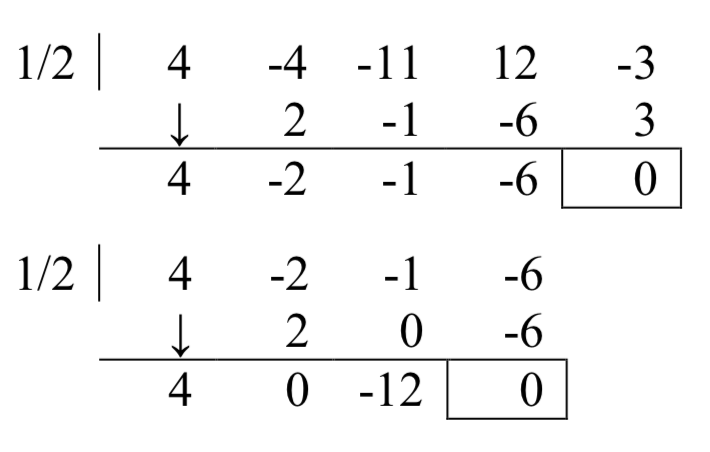
$2019-06-23 6.04.51.png$

De la primera división, obtenemos$4x^{4} -4x^{3} -11x^{2} +12x-3=\left(x-\dfrac{1}{2} \right)\left(4x^{3} -2x^{2} -x-6\right)$ La segunda división nos dice

\[4x^{4} -4x^{3} -11x^{2} +12x-3=\left(x-\dfrac{1}{2} \right)\left(x-\dfrac{1}{2} \right)\left(4x^{2} -12\right)\nonumber \]

Para encontrar las intercepciones restantes, nos fijamos$4x^{2} -12=0$ y obtenemos$x=\pm \sqrt{3}$.

Tenga en cuenta que esto también significa$4x^{4} -4x^{3} -11x^{2} +12x-3=4\left(x-\dfrac{1}{2} \right)\left(x-\dfrac{1}{2} \right)\left(x-\sqrt{3} \right)\left(x+\sqrt{3} \right)$.

Temas Importantes de esta Sección

Larga división de polinomios
Teorema del resto
Teorema de factores
División sintética de polinomios