1.3: Aplicaciones y resolución de triángulos rectos
- Page ID
- 113537
A lo largo de su desarrollo temprano, la trigonometría se utilizó a menudo como medio de medición indirecta, por ejemplo, la determinación de grandes distancias o longitudes mediante el uso de mediciones de ángulos y pequeñas distancias conocidas. Hoy en día, la trigonometría es ampliamente utilizada en física, astronomía, ingeniería, navegación, topografía y diversos campos de las matemáticas y otras disciplinas. En esta sección veremos algunas de las formas en que se puede aplicar la trigonometría. Tu calculadora debe estar en modo grado para estos ejemplos.
Una persona se para a\(150\) pies de distancia de un asta de bandera y mide un ángulo de elevación\(32^\circ\) desde su línea de visión horizontal hasta la parte superior del asta de la bandera. Supongamos que los ojos de la persona están a una distancia vertical de 6 pies del suelo. ¿Cuál es la altura del asta de la bandera?
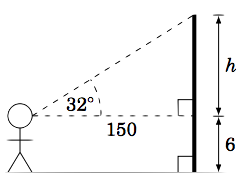
Solución:
El cuadro de la derecha describe la situación. Vemos que la altura del asta de la bandera es\(h + 6\) ft, donde
\ [\ frac {h} {150} ~=~\ tan\; 32^\ circ\ quad\ Rightarrow\ quad h ~=~ 150\;\ tan\; 32^\ circ
~=~ 150\ ;( 0.6249) ~=~ 94 ~. \ nonumber\]
¿Cómo lo sabíamos\(\tan\;32^\circ = 0.6249\,\)? Mediante el uso de una calculadora. Y como ninguno de los números que nos dieron tenía decimales, redondeamos la respuesta para\(h\) al entero más cercano. Así, la altura del asta de bandera es\(\,h + 6 = 94 + 6 = \boxed{100 ~\text{ft}}\).
Una persona de pie a\(400\) pies de la base de una montaña mide el ángulo de elevación desde el suelo hasta la cima de la montaña a ser\(25^\circ \). Luego, la persona camina\(500\) pies rectos hacia atrás y mide el ángulo de elevación hasta ahora ser\(20^\circ \). ¿Qué tan alta es la montaña?
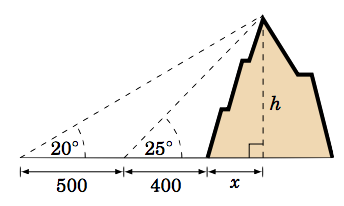
Solución:
Supondremos que el suelo es plano y no inclinado con relación a la base de la montaña. Dejar\(h\) ser la altura de la montaña, y dejar\(x\) ser la distancia desde la base de la montaña hasta el punto directamente debajo de la cima de la montaña, como en la imagen de la derecha. Entonces vemos que
\ [\ begin {alinear*}\ frac {h} {x + 400} ~=~\ tan\; 25^\ circ\ quad &\ Rightarrow\ quad h ~=~ (x + 400)\;\ tan\; 25^\ circ
~, ~\ text {y}\\ [4pt]\ frac {h} {x + 400 + 500} ~=~\ tan\; 20^\ circ\ quad &\ Rightarrow\ quad h ~=~
(x + 900)\;\ tan\; 20^\ circ,\ end {align*}\ nonumber\]
entonces
\((x + 400)\;\tan\;25^\circ ~=~ (x + 900)\;\tan\;20^\circ \), ya que ambos son iguales\(h \). Usa esa ecuación para resolver\(x\):
\ [x\;\ tan\; 25^\ circ ~-~ x\;\ tan\; 20^\ circ ~=~ 900\;\ tan\; 20^\ circ ~-~ 400\;\ tan\; 25^\ circ
\ quad\ Rightarrow\ quad
x ~=~\ frac {900\;\ tan\; 20^\ circ ~-~ 400\; bronceado\; 25^\ circ} {\ tan\; 25^\ circ ~-~\ tan\; 20^\ circ}
~=~ 1378~\ texto {ft}\ nonumber\]
Por último, sustituya\(x\) en la primera fórmula\(h\) para obtener la altura de la montaña:
\[h ~=~ (1378 + 400)\;\tan\;25^\circ ~=~ 1778\;(0.4663) ~=~ \boxed{829~ \text{ft}} \nonumber \]
Un dirigible a\(4280\) pies sobre el suelo mide un ángulo de depresión\(24^\circ\) desde su línea de visión horizontal hasta la base de una casa en el suelo. Asumiendo que el suelo es plano, ¿a qué distancia a lo largo del suelo está la casa del dirigible?
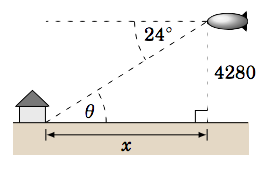
Solución:
Dejar\(x\) ser la distancia a lo largo del suelo desde el dirigible a la casa, como en la imagen a la derecha. Dado que el suelo y la línea de visión horizontal del dirigible son paralelos, sabemos por geometría elemental que el ángulo de elevación\(\theta\) desde la base de la casa hasta el dirigible es igual al ángulo de depresión desde el dirigible hasta la base de la casa, es decir\(\theta = 24^\circ \). Por lo tanto,
\ [\ frac {4280} {x} ~=~\ tan\; 24^\ circ\ quad\ Rightarrow\ quad x ~=~\ frac {4280} {\ tan\; 24^\ circ}
~=~\ en caja {9613 ~\ texto {ft}} ~. \ nonumber\]
Un observador en la cima de una montaña\(3\) millas sobre el nivel del mar mide un ángulo de depresión del\(2.23^\circ\) horizonte oceánico. Usa esto para estimar el radio de la tierra.
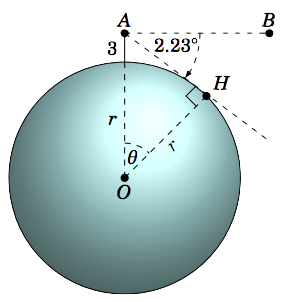
Solución:
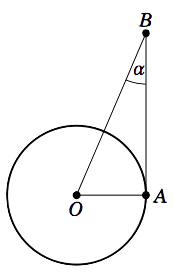
Asumiremos que la tierra es una esfera. \(r\)Sea el radio de la tierra. Dejar que el punto\(A\) represente la cima de la montaña, y dejar que\(H\) sea el horizonte oceánico en la línea de visión desde\(A \), como en la Figura 1.3.1. Dejar\(O\) ser el centro de la tierra, y dejar\(B\) ser un punto en la línea de visión horizontal desde\(A\) (es decir, en la línea perpendicular a\(\overline{OA}\)). Deja\(\theta\) ser el ángulo\(\angle\,AOH \).
Ya que\(A\) es\(3\) millas sobre el nivel del mar, tenemos\(OA = r + 3 \). También,\(OH = r \). Ahora sincev\(\overline{AB} \perp \overline{OA} \), tenemos\(\angle\,OAB = 90^\circ \), así que vemos eso\(\angle\,OAH = 90^\circ - 2.23^\circ = 87.77^\circ \). Vemos que la línea a través\(A\) y\(H\) es una línea tangente a la superficie de la tierra (considerando la superficie como el círculo de radio\(r\) a través\(H\) como en la imagen). Entonces por el Ejercicio 14 en la Sección 1.1,\(\overline{AH} \perp \overline{OH}\) y por lo tanto\(\angle\,OHA = 90^\circ \). Dado que los ángulos en el triángulo\(\triangle\,OAH\) suman\(180^\circ \), tenemos\(\theta = 180^\circ - 90^\circ - 87.77^\circ = 2.23^\circ \). Por lo tanto,
\ [\ cos\;\ theta ~=~\ frac {OH} {OA} ~=~\ frac {r} {r+3}\ quad\ Rightarrow\ quad\ frac {r} {r+3} ~=~
\ cos\; 2.23^\ circ ~,\ nonumber\]
así que resolviendo para\(r\) que obtengamos
\ [\ begin {align*}
r ~=~ (r ~+~ 3)\;\ cos\; 2.23^\ circ\ quad &\ Rightarrow\ quad
r ~-~ r\;\ cos\; 2.23^\ circ ~=~ 3\;\ cos\; 2.23^\ circ\ [4pt]
&\ cuadrilátero derecho\ r ~=~\ frac {3\;\ cos\; 2.23^\ circ} {1 ~-~\ cos\; 2.23^\ circ}\\
&\ Rightarrow\ quad\ boxed {r ~= ~ 3958.3 ~\ texto {millas}} ~.
\ end {align*}\ nonumber\]
Nota: Esta respuesta está muy cerca del radio real (medio) de\(3956.6\) millas de la tierra.
Como otra aplicación de la trigonometría a la astronomía, encontraremos la distancia de la tierra al sol. Dejar\(O\) ser el centro de la tierra, dejar\(A\) ser un punto en el ecuador, y dejar\(B\) representar un objeto (por ejemplo, una estrella) en el espacio, como en la imagen de la derecha. Si la tierra se posiciona de tal manera que el ángulo\(\angle\,OAB = 90^\circ \), entonces decimos que el ángulo\(\alpha = \angle\,OBA\) es el paralaje ecuatorial del objeto. Se ha observado que el paralaje ecuatorial del sol es aproximadamente\(\alpha =0.00244^\circ \). Usa esto para estimar la distancia desde el centro de la tierra hasta el sol.
Solución:
Deja\(B\) ser la posición del sol. Queremos encontrar la longitud de\(\overline{OB} \). Utilizaremos el radio real de la tierra, mencionado al final del Ejemplo 1.14, para obtener\(OA = 3956.6\) millas. Desde entonces\(\angle\,OAB = 90^\circ \), tenemos
\ [\ frac {OA} {OB} ~=~\ sin\;\ alfa\ quad\ Rightarrow\ quad OB ~=~\ frac {OA} {\ sin\;\ alfa} ~=~
\ frac {3956.6} {\ sin\; 0.00244^\ circ} ~=~ 92908394 ~,\ nonumber\]
por lo que la distancia desde el centro de la tierra hasta el sol es de aproximadamente\(\fbox{\(93\) millones de millas} ~.\)
Nota: La órbita terrestre alrededor del sol es una elipse, por lo que la distancia real al sol varía.
En el ejemplo anterior se utilizó un ángulo muy pequeño (\(0.00244^\circ\)). Un grado se puede dividir en unidades más pequeñas: un minuto es un sesenta de grado, y un segundo es un sesenta de minuto. El símbolo por un minuto es\('\) y el símbolo por un segundo es\('' \). Por ejemplo,\(4.5^\circ = 4^\circ\;30' \). Y\(4.505^\circ = 4^\circ\;30'\;18''\):
\[4^\circ\;30'\;18'' ~=~ 4 ~+~ \frac{30}{60} ~+~ \frac{18}{3600} ~\text{degrees} ~=~ 4.505^\circ \nonumber \]
En el Ejemplo 1.15 usamos\(\alpha = 0.00244^\circ \approx 8.8'' \), que mencionamos sólo porque algunos dispositivos de medición de ángulos sí usan minutos y segundos.
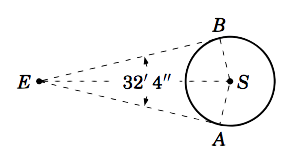
Un observador en la tierra mide un ángulo\(32'\;4''\) desde un borde visible del sol hasta el otro borde (opuesto), como en la imagen de la derecha. Usa esto para estimar el radio del sol.
Solución:
Que el punto\(E\) sea la tierra y que\(S\) sea el centro del sol. Las líneas de visión del observador a los bordes visibles del sol son líneas tangentes a la superficie del sol en los puntos\(A\) y\(B \). Así,\(\angle\,EAS = \angle\,EBS = 90^\circ \). El radio del sol es igual\(AS \). Claramente\(AS = BS \). Entonces desde\(EB = EA\) (¿por qué?) , los triángulos\(\triangle\,EAS\) y\(\triangle\,EBS\) son similares. Así,\(\angle\,AES = \angle\,BES = \frac{1}{2}\; \angle\,AEB = \frac{1}{2}\;(32'\;4'') = 16'\;2'' = (16/60) + (2/3600) = 0.26722^\circ \).
Ahora,\(ES\) es la distancia desde la superficie de la tierra (donde se encuentra el observador) hasta el centro del sol. En el Ejemplo 1.15 encontramos que la distancia desde el centro de la tierra hasta el sol es de\(92,908,394\) millas. Ya que tratamos al sol en ese ejemplo como un punto, entonces estamos justificados en tratar esa distancia como la distancia entre los centros de la tierra y el sol. Así que\(ES = 92908394 - ~\text{radius of earth} = 92908394 - 3956.6 = 92904437.4\) millas. Por lo tanto,
\ [\ sin\; (\ ángulo\, AES) ~=~\ frac {AS} {ES}\ cuádruple\ Rightarrow\ quad AS ~=~ ES\;\ sin\; 0.26722^\ circ
~=~ (92904437.4)\;\ sin\; 0.26722^\ circ ~=~\ en caja {433,293 ~\ texto {millas}}. \ nonumber\]
Nota: Esta respuesta está cerca del radio real (medio) de\(432,200\) millas del sol.
Habrás notado que las soluciones a los ejemplos que hemos mostrado requerían al menos un triángulo rectángulo. En los problemas aplicados no siempre es obvio qué triángulo rectángulo usar, razón por la cual este tipo de problemas pueden ser difíciles. A menudo ningún triángulo rectángulo será inmediatamente evidente, por lo que tendrás que crear uno. No hay una estrategia general para esto, pero recuerda que un triángulo rectángulo requiere un ángulo recto, así que busca lugares donde puedas formar segmentos de línea perpendiculares. Cuando el problema contiene un círculo, puede crear ángulos rectos usando la perpendicularidad de la línea tangente al círculo en un punto con la línea que une ese punto al centro del círculo. Lo hicimos exactamente en los Ejemplos 1.14, 1.15 y 1.16.
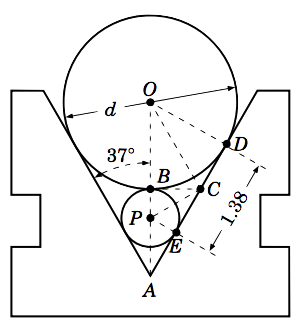
El diagrama de la máquina herramienta a la derecha muestra un bloque en V simétrico, en el que un rodillo circular se asienta sobre un rodillo circular más pequeño. Cada rodillo toca ambos lados inclinados del bloque en V. Encuentra el diámetro\(d\) del rodillo grande, dada la información en el diagrama.
Solución:
El diámetro\(d\) del rodillo grande es el doble del radio\(OB \), por lo que necesitamos encontrar\(OB \). Para ello, mostraremos que\(\triangle\,OBC\) es un triángulo rectángulo, luego encontraremos el ángulo\(\angle\,BOC \), y luego encontraremos\(BC \). La longitud\(OB\) será entonces simple de determinar.
Dado que los lados inclinados son tangentes a cada rodillo,\(\angle\,ODA = \angle\,PEC =90^\circ \). Por simetría, ya que la línea vertical a través de los centros de los rodillos hace un\(37^\circ\) ángulo con cada lado inclinado, tenemos\(\angle\,OAD = 37^\circ \). De ahí que, dado que\(\triangle\,ODA\) es un triángulo rectángulo,\(\angle\,DOA\) es el complemento de\(\angle\,OAD \). Entonces\(\angle\,DOA = 53^\circ \).
Dado que el segmento de línea horizontal\(\overline{BC}\) es tangente a cada rodillo,\(\angle\,OBC =\angle\,PBC = 90^\circ \). Así,\(\triangle\,OBC\) es un triángulo rectángulo. Y ya que\(\angle\,ODA = 90^\circ \), sabemos que\(\triangle\,ODC\) es un triángulo rectángulo. Ahora,\(OB = OD\) (ya que cada uno iguala el radio del rodillo grande), así que por el Teorema de Pitágoras tenemos\(BC = DC\):
\[BC^2 ~=~ OC^2 ~-~ OB^2 ~=~ OC^2 ~-~ OD^2 ~=~ DC^2 \quad\Rightarrow\quad BC ~=~ DC \nonumber \]
Así,\(\triangle\,OBC\) y\(\triangle\,ODC\) son triángulos congruentes (que denotamos por\(\triangle\,OBC \cong \triangle\,ODC\)), ya que sus lados correspondientes son iguales. Así, sus ángulos correspondientes son iguales. Entonces en particular,\(\angle\,BOC = \angle\,DOC \). Eso lo sabemos\(\angle\,DOB = \angle\,DOA = 53^\circ \). Por lo tanto,
\ [53^\ circ ~=~\ ángulo\, DOB ~=~\ ángulo\, BOC ~+~\ ángulo\, DOC =\ ángulo\, BOC ~+~\ ángulo\, BOC ~=~
2\;\ ángulo\, BOC\ cuádruple\ fila derecha\ cuádruple\ ángulo\, BOC ~=~ 26.5^\ circ ~. \ nonumber\]
De igual manera, desde\(BP = EP\)\(\triangle\,BPC\) y\(\angle\,PBC = \angle\,PEC = 90^\circ \), y\(\triangle\,EPC\) son triángulos rectos congruentes. Así,\(BC = EC \). Pero eso lo sabemos\(BC = DC \), y vemos por el diagrama que\(EC + DC = 1.38 \). Así,\(BC + BC = 1.38\) y así\(BC = 0.69 \). Ahora tenemos todo lo que necesitamos para encontrar\(OB\):
\ [\ frac {BC} {OB} ~=~\ tan\;\ ángulo\, BOC\ cuádruple\ Rightarrow\ quad OB ~=~\ frac {BC} {\ tan\;\ ángulo\, BOC} ~=~
\ frac {0.69} {\ tan\; 26.5^\ circ} ~=~ 1.384\ nonumber\]
De ahí que el diámetro del rodillo grande sea\(\,d = 2 \times OB = 2\,(1.384) = \boxed{2.768}\) ~.
Un mecanismo de manivela deslizante se muestra en la Figura 1.3.2 a continuación. A medida que el pistón se mueve hacia abajo, la biela gira la manivela en sentido horario, como se indica.
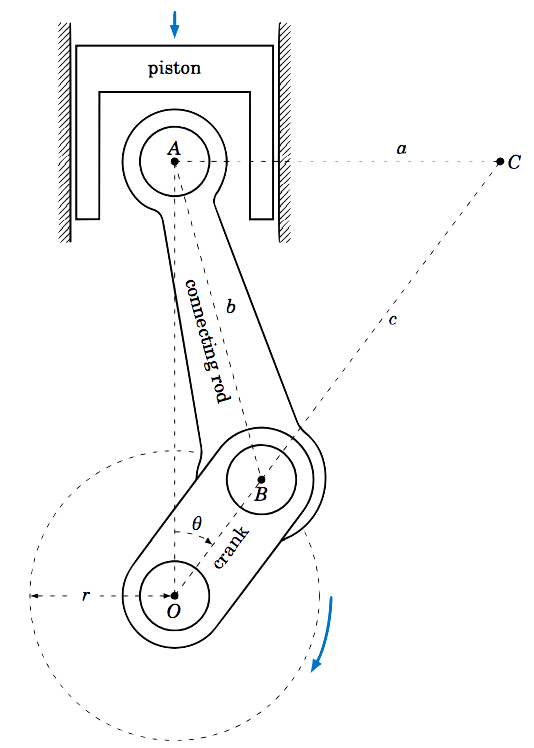
El punto\(A\) es el centro del pasador de muñeca de la biela y solo se mueve verticalmente. El punto\(B\) es el centro de la muñequilla y se mueve alrededor de un círculo de radio\(r\) centrado en el punto\(O \), que está directamente debajo\(A\) y no se mueve. A medida que la manivela gira hace un ángulo\(\theta\) con la línea\(\overline{OA} \). El centro instantáneo de rotación de la biela en un momento dado es el punto\(C\) donde la línea horizontal atraviesa\(A\) la línea extendida a través de\(O\) y\(B \). De la Figura 1.3.2 vemos eso\(\angle\,OAC = 90^\circ \), y dejamos\(a = AC \),\(b = AB \), y\(c = BC \). En los ejercicios lo demostrarás para\(0^\circ < \theta < 90^\circ \),
\ [c ~=~\ frac {\ sqrt {b^2 ~-~ r^2\; (\ sin\,\ theta) ^2}} {\ cos\;\ theta} ~\ qquad\ texto {y}\ qquad~
a ~=~ r\;\ sin\;\ theta ~+~\ sqrt {b^2 ~-~ r^2\ ;(\ sin\,\ theta) ^2} ~\ tan\;\ theta ~. \ nonumber\]
Para algunos problemas puede ayudar recordar que cuando un triángulo rectángulo tiene una hipotenusa de longitud\(r\) y un ángulo agudo\(\theta \), como en la imagen de abajo, el lado adyacente tendrá longitud\(r\,\cos\;\theta\) y el lado opuesto tendrá longitud\(r\,\sin\;\theta \). Se puede pensar en esas longitudes como los ``componentes” horizontales y verticales de la hipotenusa.
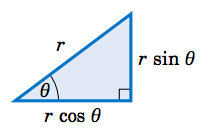
Observe en el triángulo rectángulo anterior que nos dieron dos piezas de información: uno de los ángulos agudos y la longitud de la hipotenusa. A partir de esto determinamos las longitudes de los otros dos lados, y el otro ángulo agudo es solo el complemento del ángulo agudo conocido. En general, un triángulo tiene seis partes: tres lados y tres ángulos. Resolver un triángulo significa encontrar las partes desconocidas basándose en las partes conocidas. En el caso de un triángulo rectángulo, siempre se conoce una parte: uno de los ángulos es\(90^\circ \).
Resuelve el triángulo rectángulo en la Figura 1.3.3 usando la información dada:
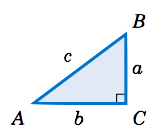
a)\(c = 10,\, A = 22^◦\)
Solución: Las partes desconocidas son\(a \)\(b \), y\(B \). Resolviendo rendimientos:
\ [\ begin {align}
a ~ &= ~ c\;\ sin\; A ~ &= ~ 10\;\ sin\; 22^\ circ ~ &= ~ 3.75\\
b ~ &= ~ c\;\ cos\; A ~ &= ~ 10\;\ cos\; 22^\ circ ~ &= ~ 9.27\
B ~ &= ~ 90^\ circ ~ A ~ &= ~ 90^\ circ ~-~ 22^\ circ ~ &= ~ 68^\ circ
\ end {align}\ nonumber\]
b)\(b = 8,\, A = 40^◦\)
Solución: Las partes desconocidas son\(a \)\(c \), y\(B \). Resolviendo rendimientos:
\[\begin{align}\frac{a}{b} ~ &= ~ \tan\;A \quad &\Rightarrow \quad a ~ &= ~ b\;\tan\;A ~ = ~8\;\tan\;40^\circ ~ = ~ 6.71\\\frac{b}{c} ~ &= ~ \cos\;A \quad &\Rightarrow \quad c ~ &= ~ \frac{b}{\cos\;A} ~ = ~\frac{8}{\cos\;40^\circ} ~ = ~ 10.44\end{align} \nonumber \]
c)\(a = 3,\, b = 4\)
Solución: Las partes desconocidas son\(c \),\(A \), y\(B \). Por el Teorema de Pitágoras,
\[c ~=~ \sqrt{a^2 ~+~ b^2} ~=~ \sqrt{3^2 ~+~ 4^2} ~=~ \sqrt{25} ~=~ 5 ~. \nonumber \]
Ahora,\(\tan\;A = \frac{a}{b} = \frac{3}{4} = 0.75 \). Entonces, ¿cómo nos encontramos\(A\)? Debe haber una clave etiquetada\(\fbox{\(\tan^{-1}\)}\) en tu calculadora, que funciona así: dale un número\(x\) y te dirá el ángulo\(\theta\) tal que\(\tan\;\theta = x \). En nuestro caso, queremos que el ángulo sea\(A\) tal que\(\tan\;A = 0.75\):
\[ \text{Enter: } 0.75 \quad \text{Press:}\fbox{\(\tan^{-1}\)} \quad \text{Answer: } 36.86989765 \nonumber \]
Esto nos dice que\(A = 36.87^\circ \), aproximadamente. Así\(B = 90^\circ - A = 90^\circ - 36.87^\circ = 53.13^\circ \).
Nota: Las claves\(\fbox{ \(\sin^{-1}\)}\) y\(\fbox{ \(\cos^{-1}\)}\) funcionan de manera similar para seno y coseno, respectivamente. Estas claves utilizan las funciones trigonométricas inversas, que discutiremos en el Capítulo 5.


