1.4: Funciones trigonométricas de cualquier ángulo
- Page ID
- 113529
Para definir las funciones trigonométricas de cualquier ángulo, incluidos los ángulos menores\(0^\circ\) o mayores que\(360^\circ \), necesitamos una definición más general de un ángulo. Decimos que un ángulo se forma girando un rayo\(\overrightarrow{OA} \) alrededor del punto final\(O \) (llamado vértice), de manera que el rayo esté en una nueva posición, denotada por el rayo\(\overrightarrow{OB} \). El rayo\(\overrightarrow{OA} \) se llama el\(\textbf{initial side}\) del ángulo, y\(\overrightarrow{OB} \) es el lado terminal del ángulo (ver Figura 1.4.1 (a)).
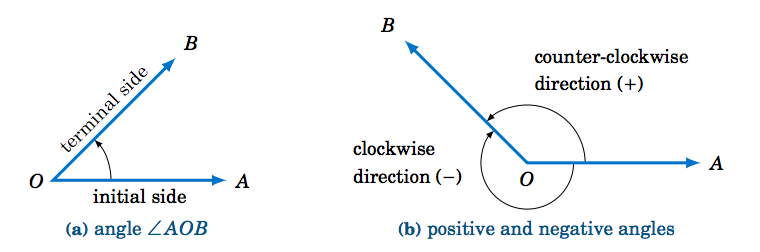
Denotamos el ángulo formado por esta rotación como\(\angle\,AOB \), o simplemente\(\angle\,O \), o incluso simplemente\(O \). Si la rotación es en sentido antihorario entonces decimos que el ángulo es positivo, y el ángulo es negativo si la rotación es en sentido horario (ver Figura 1.4.1 (b)).
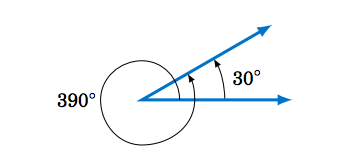
Una rotación completa en sentido antihorario de la\(\overrightarrow{OA} \) espalda sobre sí misma (llamada revolución), de manera que el lado terminal coincide con el lado inicial, es un ángulo de\(360^\circ\); en el sentido de las agujas del reloj esto sería\(-360^\circ \). No rotar\(\overrightarrow{OA} \) constituye un ángulo de\(0^\circ \). Más de una rotación completa crea un ángulo mayor que\(360^\circ \). Por ejemplo, observe eso\(30^\circ \) y\(390^\circ \) tener el mismo lado terminal en la Figura 1.4.2, ya que\(30 + 360 = 390 \).
Ahora podemos definir las funciones trigonométricas de cualquier ángulo en términos de\(\textbf{Cartesian coordinates}\). Recordemos que el plano\(\mathbf{xy}\) -coordenada consiste en puntos denotados por pares\((x,y) \) de números reales. El primer número,\(x \), es la\(\mathbf{x} \) coordenada del punto, y el segundo número,\(y \), es su\(\mathbf{y} \) coordenada. Las\(y \) coordenadas\(x \) y se miden por sus posiciones a lo largo del eje\(\mathbf{x}\)\(\mathbf{y}\) - y - eje, respectivamente, que determinan la posición del punto en el plano. Esto divide el plano\(xy\) -coordenado en cuatro cuadrantes (denotados por QI, QII, QIII, QIV), con base en los signos de\(x \) y\(y \) (ver Figura 1.4.3 (a) - (b)).
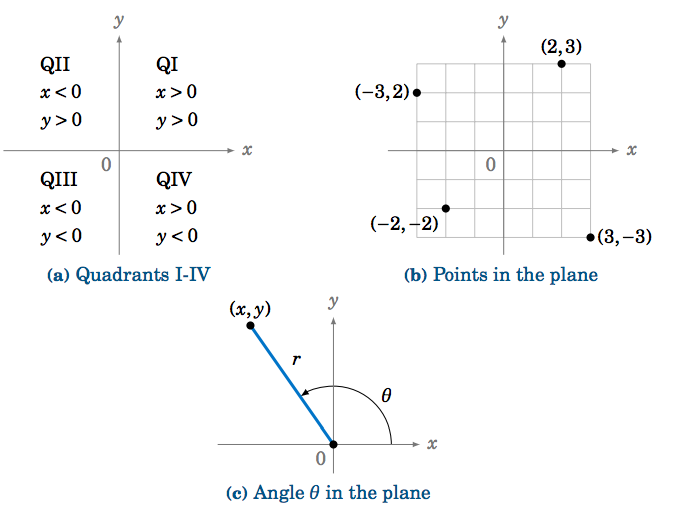
Ahora deja\(\theta \) ser cualquier ángulo. Decimos que\(\theta \) está en posición estándar si su lado inicial es el\(x\) eje positivo y su vértice es el origen\((0,0) \). Escoja cualquier punto\((x,y) \) en el lado terminal a\(\theta \) una\(r>0 \) distancia del origen (ver Figura 1.4.3 (c)). (Tenga en cuenta que\(r = \sqrt{ x^2 + y^2 } \). ¿Por qué?) Luego definimos las funciones trigonométricas de la\(\theta \) siguiente manera:
\ [\ sin\;\ theta ~=~\ dfrac {y} {r}\ qquad\ qquad
\ cos\;\ theta ~=~\ dfrac {x} {r}\ qquad\ qquad
\ tan\;\ theta ~=~\ dfrac {y} {x}\ etiqueta {1.2}\]
\ [\ csc\;\ theta ~=~\ dfrac {r} {y}\ qquad\ qquad
\ seg\;\ theta ~=~\ dfrac {r} {x}\ qquad\ qquad
\ cuna\;\ theta ~=~\ dfrac {x} {y}\ etiqueta {1.3}\]
Como en el caso agudo, mediante el uso de triángulos similares estas definiciones están bien definidas (es decir, no dependen de qué punto\((x,y) \) elegimos en el lado terminal de\(\theta\)). También, fíjese eso\(| \sin\;\theta | \le 1 \) y\( | \cos\;\theta | \le 1 \), desde\(| y | \le r \) y\( | x | \le r \) en las definiciones anteriores.
Observe que en el caso de un ángulo agudo estas definiciones son equivalentes a nuestras definiciones anteriores en términos de triángulos rectos: dibujar un triángulo rectángulo con ángulo\(\theta \) tal que\(x = \text{adjacent side} \),\(y = \text{opposite side} \), y\(r = \text{hypotenuse} \). Por ejemplo, esto nos daría\(\sin\;\theta = \frac{y}{r} = \frac{\text{opposite}}{\text{hypotenuse}} \) y\(\cos\;\theta = \frac{x}{r} = \frac{\text{adjacent}}{\text{hypotenuse}} \), igual que antes (ver Figura 1.4.4 (a)).
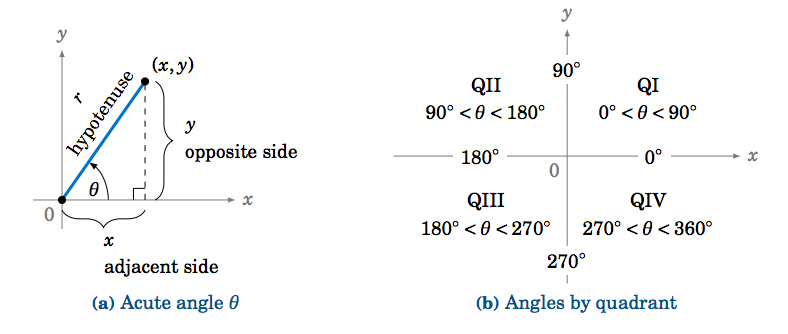
En la Figura 1.4.4 (b) vemos en qué cuadrantes o sobre qué ejes\(0^\circ \le \theta < 360^\circ \) puede caer el lado terminal de un ángulo. De la Figura 1.4.3 (a) y fórmulas Ecuación\ ref {1.2} y Ecuación\ ref {1.3}, vemos que podemos obtener valores negativos para una función trigonométrica. Por ejemplo,\(\sin\;\theta < 0 \) cuando\(y<0 \). La Figura 1.4.5 resume los signos (positivos o negativos) de las funciones trigonométricas con base en el cuadrante del ángulo:

Encuentra los valores exactos de las seis funciones trigonométricas de\(120^\circ\).
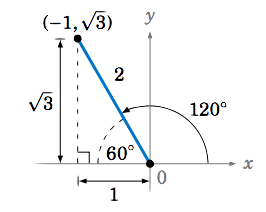
Solución
Sabemos\(120^\circ = 180^\circ - 60^\circ\). Por el Ejemplo 1.7 en la Sección 1.2, vemos que podemos usar el punto\((-1,\sqrt{3})\) en el lado terminal del ángulo\(120^\circ\) en QII, ya que vimos en ese ejemplo que un triángulo rectángulo básico con un\(60^\circ\) ángulo tiene lado adyacente de longitud\(1\), lado opuesto de longitud\(\sqrt{3}\), e hipotenusa de longitud \(2\), como en la figura de la derecha. Dibujando ese triángulo en QII para que la hipotenusa esté en el lado terminal de\(120^\circ\) marcas\(r = 2\),\(x=-1\), y\(y=\sqrt{3}\). Por lo tanto:
\ [\ nonumber\ sin\; 120^\ circ\; =\;\ dfrac {y} {r}\; =\;\ dfrac {\ sqrt {3}} {2}\ qquad
\ cos\; 120^\ circ\; =\;\ dfrac {x} {r}\; =\;\ dfrac {-1} {2}\ qqr quad
\ tan\; 120^\ circ\; =\;\ dfrac {y} {x}\; =\;\ dfrac {\ sqrt {3}} {-1}\, =\, -\ sqrt {3}\ nonumber\]
\ [\ nonúmero\ csc\; 120^\ circ\; =\;\ dfrac {r} {y}\; =\;\ dfrac {2} {\ sqrt {3}}\ qquad
\ seg\; 120^\ circ\; =\;\ dfrac {r} {x}\; =\;\ dfrac {2} {-1}\; =\; -2\ qquad
\ cuna\; 120^\ circ\; =\;\ dfrac {x} {y}\; =\;\ dfrac {-1} {\ sqrt {3}}\ nonumber\]
Encuentra los valores exactos de las seis funciones trigonométricas de\(225^\circ \).
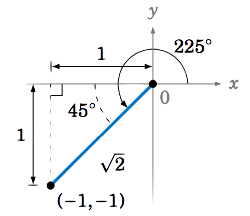
Solución
Eso lo sabemos\(225^\circ = 180^\circ + 45^\circ \). Por el Ejemplo 1.6 en la Sección 1.2, vemos que podemos usar el punto\((-1,-1) \) en el lado terminal del ángulo\(225^\circ \) en QIII, ya que vimos en ese ejemplo que un triángulo rectángulo básico con un\(45^\circ \) ángulo tiene lado adyacente de longitud\(1 \), lado opuesto de longitud\(1 \), e hipotenusa de longitud\(\sqrt{2} \), como en la figura de la derecha. Dibujando ese triángulo en QIII para que la hipotenusa esté en el lado terminal de\(225^\circ \) marcas\(r = \sqrt{2} \),\(x=-1 \), y\(y=-1 \). Por lo tanto:
\ [\ nonumber\ sin\; 225^\ circ\; =\;\ dfrac {y} {r}\; =\;\ dfrac {-1} {\ sqrt {2}}\ qquad
\ cos\; 225^\ circ\; =\;\ dfrac {x} {r}\; =\;\ dfrac {-1} {\ sqrt {2}}\ qquad
\ tan\; 225^\ circ\; =\;\ dfrac {y} {x}\; =\;\ dfrac {-1} {-1}\, =\, 1\ nonumber\]
\ [\ nonumber\ csc\; 225^\ circ\; =\;\ dfrac {r} {y}\; =\; -\ sqrt {2}\ qquad
\ seg\; 225^\ circ\; =\;\ dfrac {r} {x}\; =\; -\ sqrt {2}\ qquad
\ cot\; 225^\ circ\; =\;\ dfrac {x} {y}\; =\;\ dfrac {-1} {-1}\, =\, 1\ nonumber\]
Encuentra los valores exactos de las seis funciones trigonométricas de\(330^\circ \).
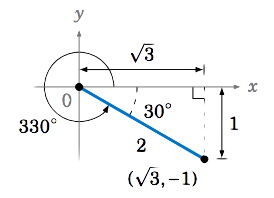
Solución
Eso lo sabemos\(330^\circ = 360^\circ - 30^\circ \). Por el Ejemplo 1.7 en la Sección 1.2, vemos que podemos usar el punto\((\sqrt{3},-1) \) en el lado terminal del ángulo\(225^\circ \) en QIV, ya que vimos en ese ejemplo que un triángulo rectángulo básico con un\(30^\circ \) ángulo tiene lado adyacente de longitud\(\sqrt{3} \), lado opuesto de longitud\(1 \), e hipotenusa de longitud \(2 \), como en la figura de la derecha. Dibujando ese triángulo en QIV para que la hipotenusa esté en el lado terminal de\(330^\circ \) marcas\(r = 2 \),\(x=\sqrt{3} \), y\(y=-1 \). Por lo tanto:
\ [\ nonumber\ sin\; 330^\ circ\; =\;\ dfrac {y} {r}\; =\;\ dfrac {-1} {2}\ qquad
\ cos\; 330^\ circ\; =\;\ dfrac {x} {r}\; =\;\ dfrac {\ sqrt {3}} {2}\ qqr quad
\ tan\; 330^\ circ\; =\;\ dfrac {y} {x}\; =\;\ dfrac {-1} {\ sqrt {3}}\ nonumber\]
\ [\ nonumber\ csc\; 330^\ circ\; =\;\ dfrac {r} {y}\; =\; -2\ qquad
\ seg\; 330^\ circ\; =\;\ dfrac {r} {x}\; =\;\ dfrac {2} {\ sqrt {3}}\ qquad
\ cuna\; 330^\ circ\; =\;\ dfrac {x} {y}\; =\; -\ sqrt {3}\ nonumber\]
Encuentre los valores exactos de las seis funciones trigonométricas de\(0^\circ \),\(90^\circ \),\(180^\circ \), y\(270^\circ \).
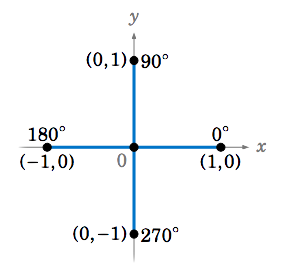
Solución
Estos ángulos son diferentes de los ángulos que hemos considerado hasta ahora, en que los lados terminales se encuentran a lo largo del\(x\) eje -eje o del\(y\) eje -eje. Entonces, a diferencia de los ejemplos anteriores, no tenemos ningún triángulo recto para dibujar. Sin embargo, los valores de las funciones trigonométricas son fáciles de calcular escogiendo los puntos más simples en sus lados terminales y luego usando las definiciones en las fórmulas Ecuación\ ref {1.2} y Ecuación\ ref {1.3}.
Por ejemplo, para el ángulo\(0^\circ \) use el punto\((1,0) \) en su lado terminal (el\(x\) eje positivo), como en la Figura 1.4.6. Se podría pensar en el segmento de línea desde el origen hasta el punto\((1,0) \) como una especie de triángulo rectángulo degenerado cuya altura es\(0 \) y cuya hipotenusa y base tienen la misma longitud\(1 \). Independientemente, en las fórmulas que usaríamos\(r = 1 \),\(x = 1 \), y\(y = 0 \). Por lo tanto:
\ [\ nonumber\ sin\; 0^\ circ\; =\;\ dfrac {y} {r}\; =\;\ dfrac {0} {1}\; =\; 0\ qquad
\ cos\; 0^\ circ\; =\;\ dfrac {x} {r}\; =\;\ dfrac {1}\; =\; 1\ qquad\ tan
\; 0^\ circ\; =\;\ dfrac {y} {x}\; =\;\ dfrac {0} {1}\; =\; =\; 0\ nonumber\]
\ [\ nonúmero\ csc\; 0^\ circ\; =\;\ dfrac {r} {y}\; =\;\ dfrac {1} {0}\; =\;\ texto {indefinido}\ qquad
\ seg\; 0^\ circ\; =\;\ dfrac {r} {x}\; =\ dfrac {1} {1}\; =\; 1\ qquad
\ cuna\; 0^\ circ\; =\;\ dfrac {x} {y}\; =\;\ dfrac {1} {0}\; =\;\ texto {indefinido}\ nonumber\]
Tenga en cuenta que\(\csc\;0^\circ \) y\(\cot\;0^\circ \) son indefinidos, ya que no\(0 \) se permite la división por.
De igual manera, a partir de la Figura 1.4.6 vemos que para\(90^\circ \) el lado terminal es el\(y\) eje positivo, así que usa el punto\((0,1) \). Nuevamente, se podría pensar en el segmento de línea desde el origen hasta\((0,1) \) como un triángulo rectángulo degenerado cuya base tiene longitud\(0 \) y cuya altura es igual a la longitud de la hipotenusa. Tenemos\(r = 1 \), y\(x = 0 \)\(y = 1 \), y por lo tanto:
\ [\ nonumber\ sin\; 90^\ circ\; =\;\ dfrac {y} {r}\; =\;\ dfrac {1} {1}\; =\; =\; 1
\ qquad\ cos\; 90^\ circ\; =\;\ dfrac {x} {r}\; =\;\ dfrac {0} {1}\; =\; 0\ qquad
\ tan\; 90^\ circ\; =\;\ dfrac {y} {x}\; =\;\ dfrac {1} {0}\; =\;\ texto {indefinido}\ nonumber\]
\ [\ nonúmero\ csc\; 90^\ circ\; =\;\ dfrac {r} {y}\; =\;\ dfrac {1} {1}\; =\; 1\ qquad
\ seg\; 90^\ circ\; =\;\ dfrac {r} {x}\; =\;\ dfrac {1} {0}\; =\;\ texto {indefinido}\ qquad
\ cuna\; 90^\ circ\; =\;\ dfrac {x} {y}\; =\;\ dfrac {0} {1}\; =\; 0\ nonumber\]
De igual manera, para\(180^\circ \) utilizar el punto\((-1,0) \) para que\(r = 1 \),\(x = -1 \), y\(y = 0 \). Por lo tanto:
\ [\ nonumber\ sin\; 180^\ circ\; =\;\ dfrac {y} {r}\; =\;\ dfrac {0} {1}\; =\; 0\ qquad
\ cos\; 180^\ circ\; =\;\ dfrac {x} {r}\; =\;\ dfrac {-1} {1}\; =\; -1\ qquad\ tan
\; 180^\ circ\; =\;\ dfrac {y} {x}\; =\;\ dfrac {0} {-1}\; =\; =\; 0\ nonumber\]
\ [\ nonumber\ csc\; 180^\ circ\; =\;\ dfrac {r} {y}\; =\;\ dfrac {1} {0}\; =\;\ text {indefinido}\ quad\;\;\;
\ seg\; 180^\ circ\; =\;\ dfrac {r} {x}\; =\; dfrac {1} {-1}\; =\; -1\ quad\;\;\;
\ cuna\; 180^\ circ\; =\;\ dfrac {x} {y}\; =\;\ dfrac {-1} {0}\; =\;\ texto {indefinido}\ nonumber\]
Por último, para\(270^\circ \) usar el punto\((0,-1) \) para que\(r = 1 \),\(x = 0 \), y\(y = -1 \). Por lo tanto:
\ [\ nonumber\ sin\; 270^\ circ\; =\;\ dfrac {y} {r}\; =\;\ dfrac {-1} {1}\; =\; =\; -1
\ qquad\ cos\; 270^\ circ\; =\;\ dfrac {x} {r}\; =\;\ dfrac {0} {1}\; =\; 0\ qquad
\ tan\; 270^\ circ\; =\;\ dfrac {y} {x}\; =\;\ dfrac {-1} {0}\; =\;\ texto {indefinido}\ nonumber\]
\ [\ nonúmero\ csc\; 270^\ circ\; =\;\ dfrac {r} {y}\; =\;\ dfrac {1} {-1}\; =\; -1\ qquad
\ seg\; 270^\ circ\; =\;\ dfrac {r} {x}\; =\;\ dfrac {1} {0}\; =\;\ texto {indefinido}\ qquad\ cuna
\; 270^\ circ\; =\;\ dfrac {x} {y}\; =\;\ dfrac {0} {-1}\; =\; =\; 0\ nonumber\]
La siguiente tabla resume los valores de las funciones trigonométricas de los ángulos entre\(0^\circ \) y\(360^\circ \) que son múltiplos enteros de\(30^\circ \) o\(45^\circ\):
Tabla 1.3 Tabla de valores de función trigonométrica
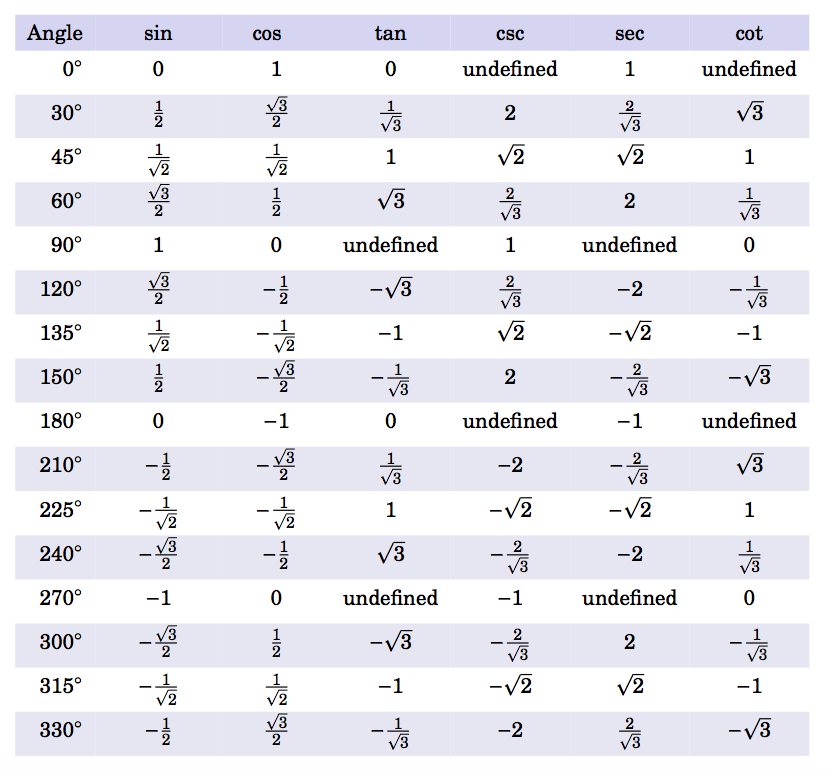
Dado que\(360^\circ \) representa una revolución completa, los valores de la función trigonométrica se repiten cada uno\(360^\circ \). Por ejemplo,\(\sin\;360^\circ = \sin\;0^\circ \),\(\cos\;390^\circ = \cos\;30^\circ \),\(\tan\;540^\circ = \tan\;180^\circ \)\(\sin\;(-45^\circ) = \sin\;315^\circ \), etc. en general, si dos ángulos difieren en un múltiplo entero de\(360^\circ\) entonces cada función trigonométrica tendrá valores iguales en ambos ángulos. Los ángulos como estos, que tienen los mismos lados inicial y terminal, se denominan coterminales.
En los Ejemplos 1.20-1.22, vimos como los valores de las funciones trigonométricas de un ángulo\(\theta \) mayor que\(90^\circ \) se encontraron usando un cierto ángulo agudo como parte de un triángulo rectángulo. Ese ángulo agudo tiene un nombre especial: si\(\theta \) es un ángulo no agudo entonces decimos que el ángulo de referencia para\(\theta \) es el ángulo agudo formado por el lado terminal de\(\theta \) y el\(x\) eje positivo o negativo. Entonces en el Ejemplo 1.20, vemos que\(60^\circ \) es el ángulo de referencia para el ángulo no agudo\(\theta = 120^\circ\); en el Ejemplo 1.21,\(45^\circ \) es el ángulo de referencia para\(\theta = 225^\circ\); y en el Ejemplo 1.22,\(30^\circ \) es el ángulo de referencia para\(\theta = 330^\circ \).
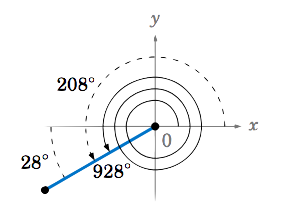
- ¿Qué ángulo entre\(0^\circ \) y\(360^\circ \) tiene el mismo lado terminal (y por lo tanto los mismos valores de función trigonométrica) que\(\theta\,\)?
- ¿Para qué sirve el ángulo de referencia\(\theta\,\)?
Solución
(a) Desde\(928^\circ = 2 \times 360^\circ + 208^\circ \) entonces\(\theta \) tiene el mismo lado terminal que\(208^\circ \), como en la Figura 1.4.7.
(b)\(928^\circ \) y\(208^\circ \) tener el mismo lado terminal en QIII, por lo que el ángulo de referencia para\(\theta = 928^\circ \) es\(208^\circ - 180^\circ = 28^\circ \).
Supongamos que\(\cos\;\theta = -\frac{4}{5} \). Encuentra los valores exactos de\(\sin\;\theta \) y\(\tan\;\theta \).
Solución
Podemos utilizar un método similar al utilizado para resolver el Ejemplo 1.8 en la Sección 1.2. Es decir, dibujar un triángulo rectángulo e interpretarlo\(\cos\;\theta \) como la relación\(\frac{\text{adjacent}}{\text{hypotenuse}} \) de dos de sus lados. Ya que\(\cos\;\theta = -\frac{4}{5} \), podemos usar\(4 \) como la longitud del lado adyacente y\(5 \) como la longitud de la hipotenusa. Por el Teorema de Pitágoras, la longitud del lado opuesto debe ser entonces\(3 \). Dado que\(\cos\;\theta \) es negativo, sabemos por la Figura 1.4.5 que\(\theta \) debe estar en QII o QIII. Así, tenemos dos posibilidades, como se muestra en la Figura 1.4.8 a continuación:
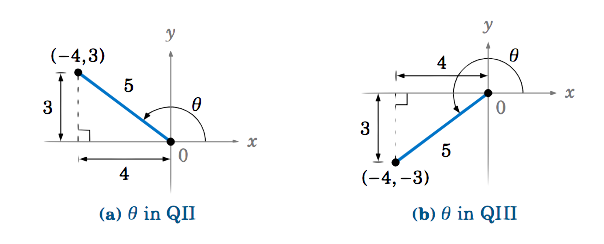
Cuando\(\theta \) está en QII, vemos en la Figura 1.4.8 (a) que el punto\((-4,3) \) está en el lado terminal de\(\theta \), y así tenemos\(x = -4 \),\(y = 3 \), y\(r = 5 \). Así,\(\sin\;\theta = \frac{y}{r} = \frac{3}{5} \) y\(\tan\;\theta = \frac{y}{x} = \frac{3}{-4} \).
Cuando\(\theta \) está en QIII, vemos en la Figura 1.4.8 (b) que el punto\((-4,-3) \) está en el lado terminal de\(\theta \), y así tenemos\(x = -4 \),\(y = -3 \), y\(r = 5 \). Así,\(\sin\;\theta = \frac{y}{r} = \frac{-3}{5} \) y\ (\ tan\;\ theta =\ frac {y} {x} =\ frac {-3} {-4} =
\ frac {3} {4}\).
Así, ya sea\(\fbox{\(\sin\;\theta = \frac{3}{5} \) y\(\tan\;\theta = -\frac{3}{4}\)}\) o\(\fbox{\(\sin\;\theta = -\frac{3}{5} \) y\(\tan\;\theta = \frac{3}{4}\)}\).
Ya que los recíprocos tienen el mismo signo,\(\csc\;\theta \) y\(\sin\;\theta \) tienen el mismo signo,\(\sec\;\theta \) y\(\cos\;\theta \) tienen el mismo signo,\(\cot\;\theta \) y\(\tan\;\theta \) tienen el mismo signo. Así que basta con recordar los signos de\(\sin\;\theta \),\(\cos\;\theta \), y\(\tan\;\theta\):
Para un ángulo\(θ\) en posición estándar y un punto\((x, y)\) en su lado terminal:
- \(\sin\;\theta \)tiene el mismo signo que\(y\)
- \(\cos\;\theta \)tiene el mismo signo que\(x\)
- \(\tan\;\theta \)es positivo cuando\(x \) y\(y \) tienen el mismo signo
- \(\tan\;\theta \)es negativo cuando\(x \) y\(y \) tienen signos opuestos


