1.5: Rotaciones y Reflexiones de Ángulos
- Page ID
- 113528
Ahora que sabemos cómo lidiar con ángulos de cualquier medida, vamos a echar un vistazo a cómo ciertas operaciones geométricas pueden ayudar a simplificar el uso de funciones trigonométricas de cualquier ángulo, y cómo se pueden hacer algunas relaciones básicas entre esas funciones. Las dos operaciones en las que nos concentraremos en esta sección son la rotación y la reflexión.
Rotar un ángulo significa girar su lado terminal alrededor del origen cuando el ángulo está en posición estándar. Por ejemplo, supongamos que giramos un ángulo\(\theta \) alrededor del origen\(90^\circ \) en sentido contrario a las agujas del reloj. En la Figura 1.5.1 vemos un ángulo\(\theta \) en QI el cual es girado por\(90^\circ \), resultando en el ángulo\(\theta + 90^\circ \) en QII. Observe que el complemento de\(\theta \) en el triángulo rectángulo en QI es el mismo que el suplemento del ángulo\(\theta + 90^\circ \) en QII, ya que la suma de\(\theta \), su complemento, e\(90^\circ \) iguales\(180^\circ \). Esto obliga a que el otro ángulo del triángulo rectángulo en la QII sea\(\theta \).
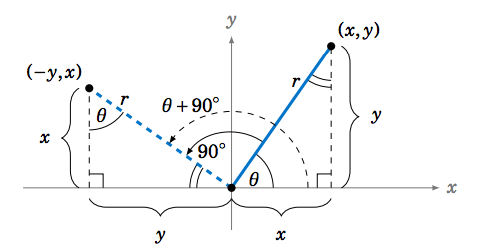
Así, el triángulo rectángulo en QI es similar al triángulo rectángulo en QII, ya que los triángulos tienen los mismos ángulos. La rotación de\(\theta \) by\(90^\circ \) no cambia la longitud\(r \) de su lado terminal, por lo que las hipotenusas de los triángulos rectos similares son iguales, y de ahí por similitud los lados restantes correspondientes también son iguales. El uso de la Figura 1.5.1 para hacer coincidir esos lados correspondientes muestra que el punto\((-y,x) \) está en el lado terminal de\(\theta + 90^\circ\) cuando\((x,y) \) está en el lado terminal de\(\theta \). De ahí que, por definición,
\ [\ nonumber\ sin\; (\ theta + 90^\ circ) ~ = ~\ frac {x} {r} ~=~\ cos\;\ theta ~, ~~
\ cos\ ;(\ theta + 90^\ circ) ~ = ~\ frac {-y} {r} ~=~ -\ sin\;\ theta ~, ~~
\ tan\ ;(\ theta + 90^\ circ) ~ = ~\ frac {x} {-y} ~=~ -\ cuna\;\ theta ~. \ nonumber\]
Aunque mostramos esto para\(\theta \) en QI, es fácil (ver Ejercicio 4) usar argumentos similares para los otros cuadrantes. En general, las siguientes relaciones se mantienen para todos los ángulos\(\theta\):
\[\sin\;(\theta + 90^\circ) ~ = ~ \cos\;\theta \label{1.4} \]
\[ \cos\;(\theta + 90^\circ) ~ = ~ -\sin\;\theta \label{1.5} \]
\[ \tan\;(\theta + 90^\circ) ~ = ~ -\cot\;\theta \label{1.6} \]
Recordemos que cualquier línea no vertical en el plano\(xy\) -coordenada puede escribirse como\(y=mx+b \), donde\(m \) está la pendiente de la línea (definida como\(m = \frac{\text{rise}}{\text{run}} \)) y\(b \) es la\(y\) intersección}, es decir, donde la línea cruza el\(y\) eje -( ver Figura 1.5.2 (a)) . Mostraremos que las pendientes de las líneas perpendiculares son recíprocas negativas. Es decir, si\(y=m_{1}x+b_1 \) y\(y=m_{2}x+b_2 \) son líneas perpendiculares no verticales y no horizontales, entonces\(m_2 = -\frac{1}{m_1} \) (ver Figura 1.5.2 (b)).
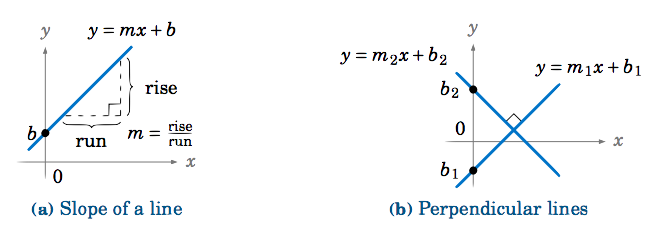
Primero, supongamos que una línea\(y=mx+b \) tiene pendiente distinta de cero. La línea cruza el\(x\) eje -eje en alguna parte, así que deja\(\theta \) ser el ángulo que el\(x\) eje positivo hace con la parte de la línea por encima del\(x\) eje -como en la Figura 1.5.3. Porque\(m > 0 \) vemos que\(\theta \) es agudo y\(\tan\;\theta = \frac{\text{rise}}{\text{run}} = m \).
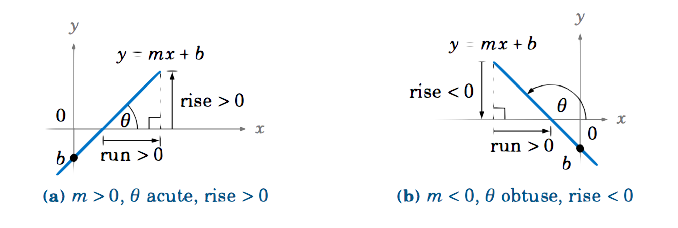
Si\(m < 0 \), entonces vemos que\(\theta \) es obtuso y la subida es negativa. Dado que la carrera siempre es positiva, nuestra definición de\(\tan\;\theta \) desde la Sección 1.4 significa que\(\tan\;\theta = \frac{-\text{rise}}{-\text{run}} = \frac{\text{rise}}{\text{run}} = m \) (imagínese en la Figura 1.5.3 (b) que toda la línea se desplaza horizontalmente para pasar por el origen, de manera que eso no\(\theta \) se modifica y el punto\((-\text{run},-\text{rise}) \) está en el lado terminal de\(\theta\)). Por lo tanto:
Para una línea\(y=mx+b \) con\(m \ne 0 \), la pendiente viene dada por\(m = \tan\;\theta\, \), donde\(\theta \) está el ángulo formado por el\(x\) eje positivo y la parte de la línea por encima del\(x\) eje.}
Ahora, en la Figura 1.5.2 (b) vemos que si dos líneas\(y=m_{1}x+b_1 \) y\(y=m_{2}x+b_2 \) son perpendiculares entonces girar una línea en sentido antihorario\(90^\circ \) alrededor del punto de intersección nos da la segunda línea. Entonces, si\(\theta \) es el ángulo que\(y=m_{1}x+b_1 \) hace la línea con el\(x\) eje positivo, entonces\(\theta + 90^\circ \) es el ángulo que la línea\(y=m_{2}x+b_2 \) hace con el\(x\) eje positivo. Entonces por lo que acabamos de mostrar,\(m_1 = \tan\;\theta \) y\(m_2 = \tan\;(\theta + 90^\circ) \). Pero por fórmula Ecuación\ ref {1.6} eso lo sabemos\(\tan\;(\theta + 90^\circ) = -\cot\;\theta \). De ahí,\(m_2 = -\cot\;\theta = -\frac{1}{\tan\;\theta} = -\frac{1}{m_1} \). \(\textbf{QED}\)
Girar un ángulo\(90^\circ \) en\(\theta \) el sentido de las agujas del reloj da como resultado el ángulo\(\theta - 90^\circ \). Podríamos usar otro argumento geométrico para derivar relaciones trigonométricas que involucren\(\theta - 90^\circ \), pero es más fácil usar un simple truco: ya que las ecuaciones\ ref {1.4} -\ ref {1.6} se mantienen para cualquier ángulo\(\theta \), simplemente\(\theta \) reemplazarlas por\(\theta - 90^\circ \) en cada fórmula. Ya que\((\theta - 90^\circ) + 90^\circ = \theta \), esto nos da:
\[\label{1.7} \sin\;(\theta - 90^\circ) ~ = ~ -\cos\;\theta \]
\[\label{1.8} \cos\;(\theta - 90^\circ) ~ = ~ \sin\;\theta \]
\[\label{1.9}\tan\;(\theta - 90^\circ) ~ = ~ -\cot\;\theta \]
Consideramos ahora rotar un ángulo\(\theta \) por\(180^\circ \). Observe en la Figura 1.5.4 que los ángulos\(\theta \pm 180^\circ \) tienen el mismo lado terminal, y están en el cuadrante opuesto\(\theta \).
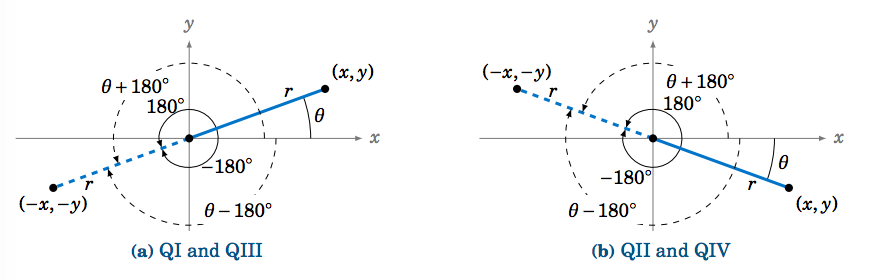
Ya que\((-x,-y) \) está en el lado terminal de\(\theta \pm 180^\circ \) cuando\((x,y) \) está en el lado terminal de\(\theta \), obtenemos las siguientes relaciones, que se mantienen para todos\(\theta\):
\[\label{1.10}\sin\;(\theta \pm 180^\circ) ~ = ~ -\sin\;\theta \]
\[\label{1.11} \cos\;(\theta \pm 180^\circ) ~ = ~ -\cos\;\theta \]
\[\label{1.12}\tan\;(\theta \pm 180^\circ) ~ = ~ \tan\;\theta \]
Un reflejo es simplemente la imagen especular de un objeto. Por ejemplo, en la Figura 1.5.5 el objeto original está en QI, su reflexión alrededor del\(y\) eje es en QII, y su reflexión alrededor del\(x\) eje es en QIV. Observe que si primero reflejamos el objeto en QI alrededor del\(y\) eje -y luego seguimos eso con una reflexión alrededor del\(x\) eje -eje, obtenemos una imagen en QIII. Esa imagen es el reflejo alrededor del origen del objeto original, y equivale a una rotación de\(180^\circ \) alrededor del origen. Observe también que una reflexión alrededor del\(y\) eje es equivalente a una reflexión alrededor del\(x\) eje seguido de una rotación\(180^\circ \) alrededor del origen.
Aplicando esto a los ángulos, vemos que la reflexión de un ángulo\(\theta \) alrededor del\(x\) eje -es el ángulo\(-\theta \), como en la Figura 1.5.6.
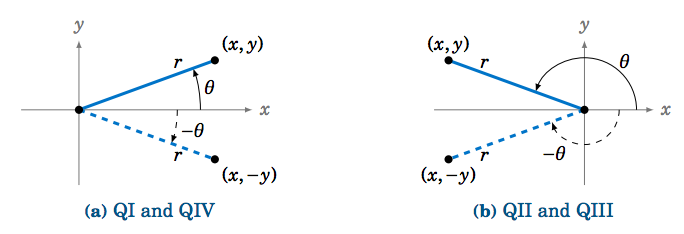
Entonces vemos que reflejando un punto\((x,y) \) alrededor del\(x\) eje -solo reemplaza\(y \) por\(-y \). Por lo tanto:
\[\label{1.13}\sin\;(-\theta) ~ = ~ -\sin\;\theta \]
\[\label{1.14} \cos\;(-\theta) ~ = ~ \cos\;\theta \]
\[\label{1.15} \tan\;(-\theta) ~ = ~ -\tan\;\theta \]
Observe que la función coseno no cambia en la Ecuación\ ref {1.14} porque depende de\(x \), y no de\(y \), para un punto\((x,y) \) en el lado terminal de\(\theta \).
En general, una función\(f(x) \) es una función par si\(f(-x) = f(x)\) para todos\(x \), y se llama una función impar si\(f(-x) = -f(x) \) para todos\(x \). Así, la función coseno es par, mientras que las funciones seno y tangente son impares.
Reemplazar\(\theta \) por\(-\theta \) en Ecuaciones\ ref {1.4} -\ ref {1.6}, luego usando Ecuaciones\ ref {1.13} -\ ref {1.15}, da:
\[\label{1.16}\sin\;(90^\circ - \theta) ~ = ~ \cos\;\theta \]
\[\label{1.17}\cos\;(90^\circ - \theta) ~ = ~ \sin\;\theta \]
\[\label{1.18}\tan\;(90^\circ - \theta) ~ = ~ \cot\;\theta \]
Tenga en cuenta que las Ecuaciones\ ref {1.16} -\ ref {1.18} extienden el Teorema de la Cofunción desde la Sección 1.2 a todos\(\theta \), no solo a los ángulos agudos. Del mismo modo, las ecuaciones\ ref {1.10} -\ ref {1.12} y\ ref {1.13} -\ ref {1.15} dan:
\[\label{1.19} \sin\;(180^\circ - \theta) ~ = ~ \sin\;\theta \]
\[\label{1.20}\cos\;(180^\circ - \theta) ~ = ~ -\cos\;\theta \]
\[\label{1.21}\tan\;(180^\circ - \theta) ~ = ~ -\tan\;\theta \]
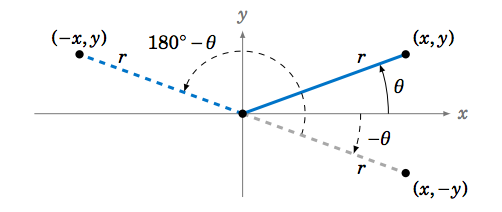
Observe que la reflexión alrededor\(y\) del eje es equivalente a la reflexión alrededor\(x\) del eje (\(\theta \mapsto -\theta\)) seguida de una rotación de\(180^\circ \) (\(-\theta \mapsto -\theta + 180^\circ = 180^\circ - \theta\)), como en la Figura 1.5.7.
Puede parecer que estas operaciones geométricas y fórmulas no son necesarias para evaluar las funciones trigonométricas, ya que solo podríamos usar una calculadora. No obstante, hay dos razones por las que son útiles. En primer lugar, las fórmulas funcionan para cualquier ángulo, por lo que a menudo se utilizan para probar fórmulas generales en matemáticas y otros campos, como veremos más adelante en el texto. En segundo lugar, pueden ayudar a determinar qué ángulos tienen un valor de función trigonométrica dado.
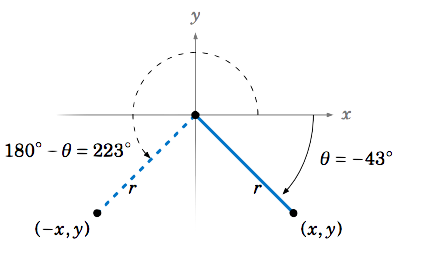
Encuentra todos los ángulos\(0^\circ \le \theta < 360^\circ \) tal que\(\sin\;\theta = -0.682 \).
Solución
Usando el botón\(\fbox{\(\sin^{-1}\)}\) en una calculadora con\(-0.682 \) como entrada, obtenemos\(\theta = -43^\circ \), que no está entre\(0^\circ \) y\(360^\circ \). Ya que\(\theta = -43^\circ \) está en QIV, su reflexión\(180^\circ - \theta \) alrededor del\(y\) eje -será en QIII y tendrá el mismo valor sinusoidal. Pero\(180^\circ - \theta = 180^\circ - (-43^\circ) = 223^\circ \) (ver Figura 1.5.8). También, lo sabemos\(-43^\circ \) y\(-43^\circ + 360^\circ = 317^\circ \) tenemos los mismos valores de función trigonométrica. Entonces como los ángulos en QI y QII tienen valores sinusoidales positivos, vemos que los únicos ángulos entre\(0^\circ \) y\(360^\circ \) con un seno de\(-0.682 \) son\(\boxed{\theta = 223^\circ ~\text{and}~ 317^\circ}~ \).