1.E: Ángulos trigonométricos de triángulo recto (ejercicios)

Estos son ejercicios de tarea para acompañar el mapa de texto “Trigonometría Primaria” de Corral. Se trata de un texto sobre trigonometría elemental, diseñado para estudiantes que han cursado cursos de álgebra y geometría de secundaria. Aunque está diseñado para estudiantes universitarios, también podría usarse en escuelas secundarias. Se cubren los temas tradicionales, pero se toma un enfoque más geométrico de lo habitual. También se discuten algunos métodos numéricos (por ejemplo, el método secante para resolver ecuaciones trigonométricas).

1.1 Ejercicios

Para los Ejercicios 1-4, encuentra el valor numérico del ángulo (s) indicado (s) para el triángulo\(\triangle\,ABC \).

1.1.1 Averiguar\(B \) si\(A = 15^\circ \) y\(C = 50^\circ \).

1.1.2 Averiguar\(C \) si\(A = 110^\circ \) y\(B = 31^\circ \).

1.1.3 Buscar\(A \) y\(B \) si\(C = 24^\circ \),\(A = \alpha \), y\(B = 2\alpha \).

1.1.4 Encontrar\(A \),\(B \), y\(C \) si\(A = \beta \) y\(B = C = 4\beta \).

Para Ejercicios 5-8, encuentra el valor numérico del ángulo o ángulos indicados para el triángulo rectángulo\(\triangle\,ABC \),\(C \) siendo el ángulo recto.

1.1.5 Averiguar\(B \) si\(A = 45^\circ \).

1.1.6 Buscar\(A \) y\(B \) si\(A = \alpha \) y\(B = 2\alpha \).

1.1.7 Encontrar\(A \) y\(B \) si\(A = \phi \) y\(B = \phi^2 \).

1.1.8 Buscar\(A \) y\(B \) si\(A = \theta \) y\(B = 1/\theta \).

1.1.9 Un automóvil va 24 millas hacia el norte y luego 7 millas hacia el este. ¿Cuál es la distancia recta entre el punto de partida y el punto final del automóvil?

1.1.10 Un extremo de una cuerda está unido a la parte superior de un poste de 100 pies de altura. Si la cuerda mide 150 pies de largo, ¿cuál es la distancia máxima a lo largo del suelo desde la base del poste hasta donde se puede unir el otro extremo? Se puede suponer que el poste es perpendicular al suelo.

1.1.11 Demostrar que la hipotenusa es el lado más largo de cada triángulo rectángulo. (Pista:\(a^2 + b^2 > a^2\) ¿Es?)

1.1.12 ¿Puede un triángulo rectángulo tener lados con longitudes 2, 5 y 6? Explique su respuesta.

1.1.13 Si las longitudes\(a \),\(b \), y\(c \) de los lados de un triángulo rectángulo son enteros positivos, con\(a^2 + b^2 = c^2 \), entonces forman lo que se llama un triple pitagórico. El triple normalmente se escribe como (\(a \),\(b \),\(c\)). Por ejemplo, (3,4,5) y (5,12,13) son triples pitagóricos bien conocidos.
(a) Demostrar que (6,8,10) es un triple pitagórico.
(b) Demostrar que si (\(a \)\(b \),,\(c\)) es un triple pitagórico entonces así es (\(ka \),\(kb \),\(kc\)) para cualquier entero\(k >0 \). ¿Cómo interpretarías esto geométricamente?
(c) Demostrar que (\(2mn \)\(m^2 - n^2 \),,\(m^2 + n^2\)) es un triple pitagórico para todos los enteros\(m > n > 0 \).
d) El triple en la parte c) se conoce como la fórmula de Euclides para generar triples pitagóricos. Anote los primeros diez triples pitagóricos generados por esta fórmula, es decir, usar:\(m=2 \) y\(n=1\);\(m=3 \) y\(n=1 \),\(2\);\(m=4 \) y\(n=1 \),\(2 \),\(3\);\(m=5 \) y\(n=1 \),,,\(2 \),\(3 \),\(4 \).

1.1.14 Este ejercicio describirá cómo dibujar una línea a través de cualquier punto fuera de un círculo de tal manera que la línea intersecta al círculo en un solo punto. Esto se denomina línea tangente al círculo (ver la imagen de la izquierda en la Figura 1.1.6), noción que utilizaremos a lo largo del texto.

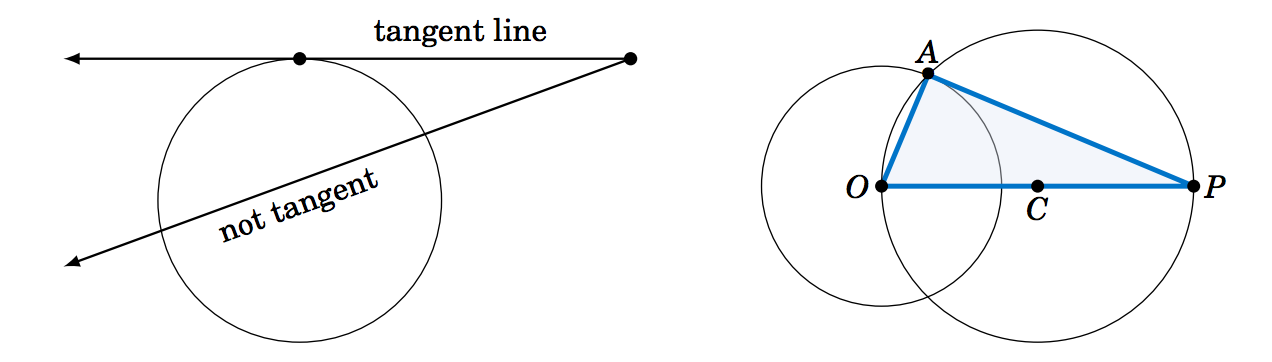
Figura 1.1.6

En una hoja de papel dibuje un círculo de radio de 1 pulgada, y llame al centro de ese círculo\(O \). Elija un punto\(P \) que esté a\(2.5 \) centímetros de distancia\(O \). Dibuja el círculo que tiene\(\overline{OP} \) como diámetro, como en la imagen de la derecha en la Figura 1.1.6. \(A \)Sea uno de los puntos donde este círculo se cruza con el primer círculo. Dibuja la línea a través\(P \) y\(A \). En general la línea tangente a través de un punto en un círculo es perpendicular a la línea que une ese punto al centro del círculo (¿por qué?). Utilice este hecho para explicar por qué la línea que dibujó es la línea tangente a través\(A \) y para calcular la longitud de\(\overline{PA} \). ¿Coincide con la medición física de\(\overline{PA}\)?

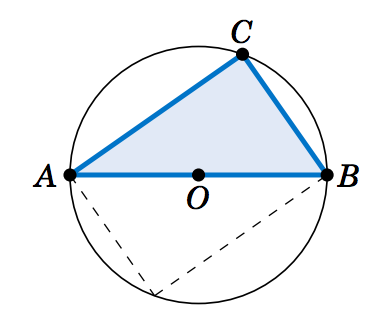
1.1.15 Supongamos que\(\triangle\,ABC \) es un triángulo con lado\(\overline{AB} \) un diámetro de un círculo con centro\(O \), como en la imagen de la derecha, y supongamos que el vértice\(C \) se encuentra en el círculo. Ahora imagina que giras el círculo\(180^\circ \) alrededor de su centro, de manera que\(\triangle\,ABC \) esté en una nueva posición, como lo indican las líneas discontinuas en la imagen. Explica cómo esta imagen prueba el Teorema de Tales.

---

1.2 Ejercicios

Para los Ejercicios 1-10, encuentra los valores de las seis funciones trigonométricas de\\ ángulos\(A\) y\(B \) en el triángulo rectángulo\(\triangle\,ABC \) en la Figura 1.2.3.

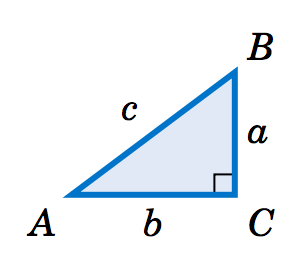
Figura 1.2.3

1.2.1\(a = 5 \),\(b = 12 \),\(c = 13\)

1.2.2\(a = 8 \),\(b = 15 \),\(c = 17\)

1.2.3\(a = 7 \),\(b = 24 \),\(c = 25\)

1.2.4\(a = 20 \), \(b = 21 \),\(c = 29\)

1.2.5\(a = 9 \),\(b = 40 \),\(c = 41\)

1.2.6\(a = 1 \),\(b = 2 \),\(c = \sqrt{5}\)

1.2.7\(a = 1 \),\(b = 3\)

1.2.8\(a = 2 \),\(b = 5\)

1.2.9\(a = 5 \),\(c = 6\)

1.2.10\(b = 7 \),\(c = 8\)

Para los Ejercicios 11-18, encuentra los valores del otras cinco funciones trigonométricas del ángulo agudo\(A \) dado el valor indicado de una de las funciones.

1.2.11\(\sin\;A = \frac{3}{4}\)

1.2.12\(\cos\;A = \frac{2}{3}\)

1.2.13\(\cos\;A = \frac{2}{\sqrt{10}}\)

1.2.14\(\sin\;A = \frac{2}{4}\)

1.2.15\(\tan\;A = \frac{5}{9}\)

1.2.16\(\tan\;A = 3\)

1.2.17\(\sec\;A = \frac{7}{3}\)

1.2.18\(\csc\;A = 3\)

Para Ejercicios 19-23, escribir el dado número como una función trigonométrica de un ángulo agudo menor que\(45^\circ \).

1.2.19\(\sin\;87^\circ\)

1.2.20\(\sin\;53^\circ\)

1.2.21\(\cos\;46^\circ\)

1.2.22\(\tan\;66^\circ\)

1.2.23\(\sec\;77^\circ\)

Para los Ejercicios 24-28, escriba el número dado como una función trigonométrica de un ángulo agudo mayor que\(45^\circ \).

1.2.24\(\sin\;1^\circ\)

1.2.25\(\cos\;13^\circ\)

1.2.26\(\tan\;26^\circ\)

1.2.27\(\cot\;10^\circ\)

1.2.28\(\csc\;43^\circ\)

1.2.29 En el Ejemplo 1.7 encontramos los valores de las seis funciones trigonométricas de\(60^\circ \) y\(30^\circ \).

(a) ¿Lo hace\(\;\sin\;30^\circ ~+~ \sin\;30^\circ ~=~ \sin\;60^\circ\)?
b) ¿Lo hace\(\;\cos\;30^\circ ~+~ \cos\;30^\circ ~=~ \cos\;60^\circ\)?
(c) ¿Lo hace\(\;\tan\;30^\circ ~+~ \tan\;30^\circ ~=~ \tan\;60^\circ\)?
d) ¿Lo hace\(\;2\,\sin\;30^\circ\,\cos\;30^\circ ~=~ \sin\;60^\circ\)?

1.2.30 Para un ángulo agudo\(A \), ¿puede\(\sin\;A \) ser mayor que\(1\)? Explique su respuesta.

1.2.31 Para un ángulo agudo\(A \), ¿puede\(\cos\;A \) ser mayor que\(1\)? Explique su respuesta.

1.2.32 Para un ángulo agudo\(A \), ¿puede\(\sin\;A \) ser mayor que\(\tan\;A\)? Explique su respuesta.

1.2.33 Si\(A \) y\(B \) son ángulos agudos y\(A < B \), explicar por qué\(\sin\;A < \sin\;B \).

1.2.34 Si\(A \) y\(B \) son ángulos agudos y\(A < B \), explicar por qué\(\cos\;A > \cos\;B \).

1.2.35 Demostrar el Teorema de la Cofunción (Teorema 1.2). (Pista: Dibuja un triángulo rectángulo y etiqueta los ángulos y los lados.)

1.2.36 Utilice el Ejemplo 1.10 para encontrar las seis funciones trigonométricas de\(15^\circ \).

1.2.37 En la Figura 1.2.4,\(\overline{CB} \) es un diámetro de un círculo con un radio de\(2 \) cm y centro\(O \),\(\triangle\,ABC \) es un triángulo rectángulo, y\(\overline{CD}\) tiene longitud\(\sqrt{3} \) cm.

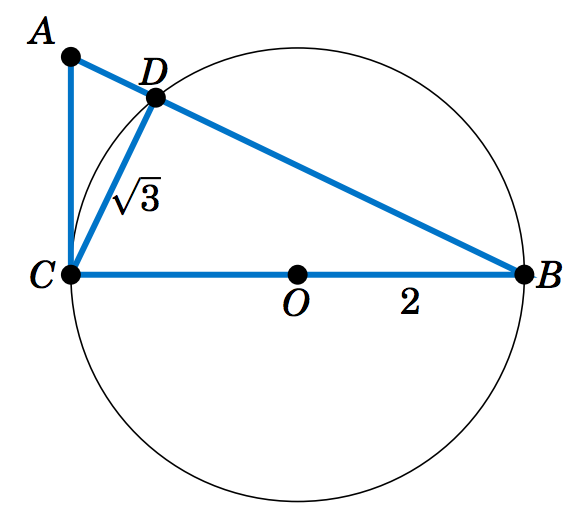
Figura 1.2.4

(a) Encontrar\(\;\sin\;A \). (Pista: Usa el Teorema de Thalos. )
(b) Encontrar la longitud de\(\;\overline{AC} \).
(c) Encontrar la longitud de\(\;\overline{AD} \).
d) La figura 1.2.4 se dibuja a escala. Usa un Transportador para medir el ángulo\(A \), luego usa tu calculadora para encontrar\\ el seno de ese ángulo. ¿El resultado de la calculadora está cerca de tu respuesta de la parte (a)? Nota: Asegúrate de que tu calculadora esté en modo grado.


1.2.38 En el Ejercicio 37, verificar que el área de\(\triangle\,ABC \) iguales\(\frac{1}{2} AB \cdot CD \). ¿Por qué tiene sentido esto?

1.2.39 En el Ejercicio 37, verificar que el área de\(\triangle\,ABC \) iguales\(\frac{1}{2} AB \cdot AC \; \sin\;A \).

1.2.40 En el Ejercicio 37, verificar que el área de\(\triangle\,ABC \) iguales\(\frac{1}{2} (BC)^2 \;\cot\;A \).

---

1.3 Ejercicios

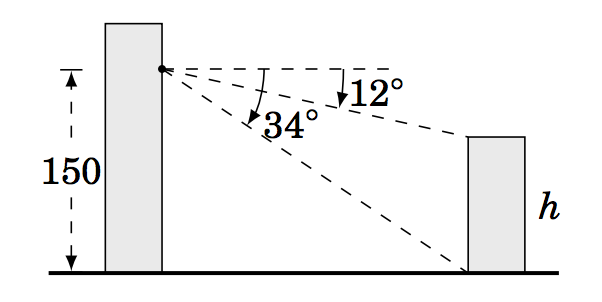
1.3.1 Desde una posición\(150 \) ft sobre el suelo, un observador en un edificio mide los ángulos de depresión de\(12^\circ \) y\(34^\circ \) hacia la parte superior e inferior, respectivamente, de un edificio más pequeño, como en la imagen de la derecha. Usa esto para encontrar la altura\(h \) del edificio más pequeño.

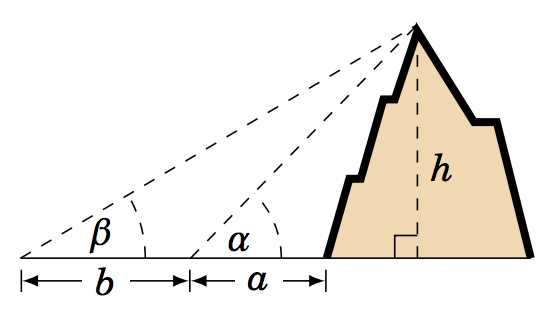
1.3.2 Generalizar Ejemplo 1.12: Una persona de pie a\(a \) pies de la base de una montaña mide un ángulo de elevación\(\alpha \) desde el suelo hasta la cima de la montaña. Luego, la persona camina\(b \) pies rectos hacia atrás y mide un ángulo de elevación\(\beta \) hasta la cima de la montaña, como en la imagen de la derecha. Asumiendo que el suelo está nivelado, encuentra una fórmula para la altura\(h \) de la montaña en términos de\(a \)\(b \),,\(\alpha \), y\(\beta \).

1.3.3 A medida que el ángulo de elevación desde la cima de una torre hasta el sol disminuye de\(64^\circ \) a\(49^\circ \) durante el día, la longitud de la sombra de la torre aumenta en\(92 \) pies a lo largo del suelo. Asumiendo que el suelo está nivelado, encuentra la altura de la torre.

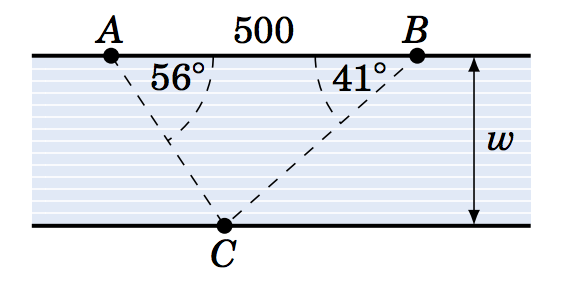
1.3.4 Dos orillas de un río son paralelas, y la distancia entre dos puntos\(A \) y\(B \) a lo largo de una orilla es de\(500 \) pies. Por un punto\(C \) en la orilla opuesta,\(\angle\,BAC = 56^\circ \) y\(\angle\,ABC = 41^\circ \), como en la imagen de la derecha. ¿Cuál es el ancho\(w \) del río? (Pista: Dividir\(\overline{AB} \) en dos piezas. )

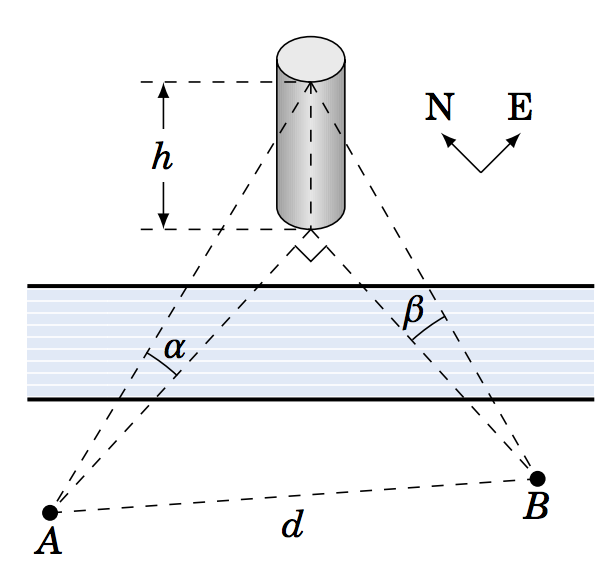
1.3.5 Una torre a un lado de un río se encuentra directamente al este y al norte de los puntos\(A \) y\(B \), respectivamente, al otro lado del río. La parte superior de la torre tiene ángulos de elevación\(\alpha\) y\(\beta \) desde\(A \) y\(B \), respectivamente, como en la imagen de la derecha. Deja\(d \) ser la distancia entre\(A \) y\(B \). Suponiendo que ambos lados del río están a la misma elevación, mostrar que la altura\(h \) de la torre es
\ [\ nonumber
h ~=~\ frac {d} {\ sqrt {(\ cot\,\ alpha) ^2 ~+~ (\ cot\,\ beta) ^2}} ~.
\]

1.3.6 Se ha observado que el paralaje ecuatorial de la luna es aproximadamente\(57' \). Tomando que el radio de la tierra sea\(3956.6 \) millas, estime la distancia desde el centro de
la tierra hasta la luna. (Pista: Ver Ejemplo 1.15.)

1.3.7 Un observador en la tierra mide un ángulo\(31'\;7'' \) desde un borde visible de la luna hasta el otro borde (opuesto). Usa esto para estimar el radio de la luna. (Pista: Utilice el Ejercicio
6 y vea el Ejemplo 1.16. )

1.3.8 Un rodamiento de bolas se asienta entre dos ranuras metálicas, con la ranura superior teniendo un ángulo de\(120^\circ \) y la ranura inferior teniendo un ángulo de\(90^\circ \), como en la imagen de la derecha. ¿Cuál debe ser el diámetro del rodamiento de bolas para que la distancia entre los vértice de las ranuras sea de media pulgada? Puede suponer que el vértice superior está directamente por encima del vértice inferior.

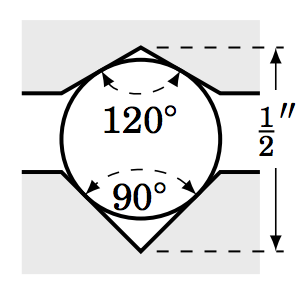
1.3.9 El diagrama de la máquina herramienta a la derecha muestra una rosca sinfín simétrica, en la que se asienta un rodillo circular de\(1.5 \) pulgadas de diámetro. Encuentra la cantidad\(d \) que la parte superior del rodillo se eleva por encima de la parte superior del hilo, dada la información en el diagrama. (Pista: Extiende los lados inclinados del hilo hasta que se encuentren en un punto. )

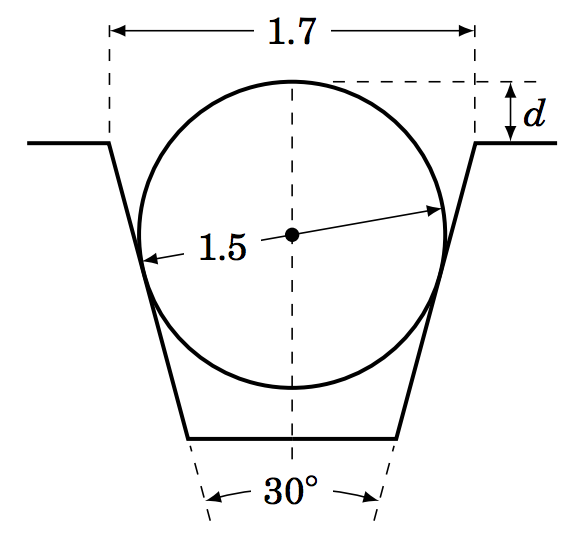
1.3.10 Repita el Ejercicio 9 usando\(1.8 \) pulgadas como la distancia a través de la parte superior de la rosca del gusano.

1.3.11 En el Ejercicio 9, ¿cuál tendría que ser la distancia a través de la parte superior del hilo de gusano para hacer\(d \) igual a\(0 \) pulgadas?

1.3.12 Porque\(0^\circ < \theta < 90^\circ \) en el mecanismo de manivela deslizante del Ejemplo 1.18, mostrar que
\ [\ nonumber
c ~=~\ frac {\ sqrt {b^2 ~-~ r^2\ ;(\ sin\,\ theta) ^2}} {\ cos\;\ theta} ~\ qquad\ text {y}\ qquad~
a ~=~ r\;\ sin\; theta\; eta ~+~\ sqrt {b ^2 ~-~ r^2\; (\ sin\,\ theta) ^2} ~\ tan\;\ theta ~.
\]
(Sugerencia: En la Figura 1.3.2 dibuje segmentos de línea de\(B \) perpendicular a\(\overline{OA} \) y\(\overline{AC} \).)

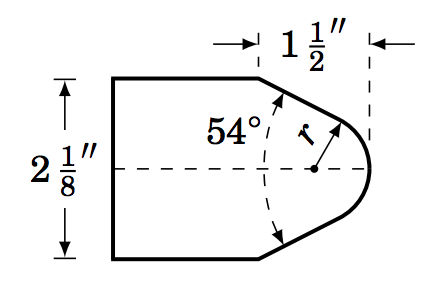
1.3.13 El diagrama de la máquina herramienta a la derecha muestra un troquel simétrico. En esta vista, la punta redondeada es parte de un círculo de radio\(r \), y los lados inclinados son tangentes a ese círculo y forman un ángulo de\(54^\circ \). Los lados superior e inferior del troquel son horizontales. Usa la
información del diagrama para encontrar el radio\(r \).

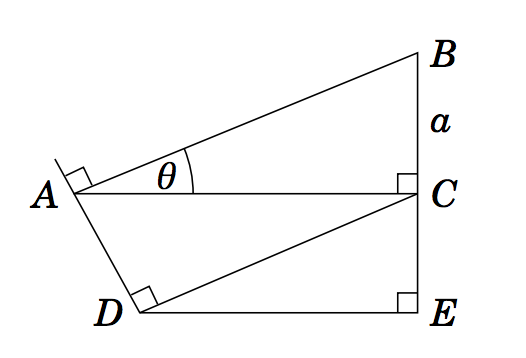
1.3.14 En la figura de la derecha,\(\angle\,BAC = \theta \) y\(BC = a \). Use esto para encontrar\(AB \),\(AC \),\(AD \)\(DC \),\(CE \), y\(DE \) en términos de\(\theta \) y\(a \). (Pista: ¿Cuál es el ángulo\(\angle\,ACD\,\)?)

Para los Ejercicios 15-23, resuelve el triángulo rectángulo en la Figura 1.3.4 usando la información dada.

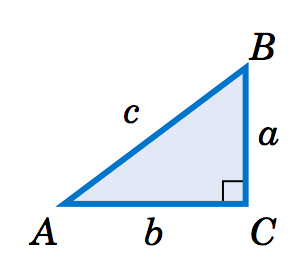
Figura 1.3.4

1.3.15\(a = 5 \),\(b = 12\)

1.3.16\(c = 6 \),\(B = 35^\circ\)

1.3.17\(b = 2 \),\(A = 8^\circ\)

1.3.18\(a = 2 \),\(c = 7\)

1.3.19\(a = 3 \),\(A = 26^\circ\)

1.3.20\(b = 1 \),\(c = 2\)

1.3.21\(b = 3 \),\(B = 26^\circ\)

1.3.22\(a = 2 \),\(B = 8^\circ\)

1.3.23\(c = 2 \),\(A = 45^\circ\)

1.3.24 En el Ejemplo 1.10 en la Sección 1.2, encontramos la exacta valores de las seis funciones trigonométricas de\(75^\circ \). Por ejemplo, mostramos que\ (\ cot\; 75^\ circ =\ frac {\ sqrt {6} -
\ sqrt {2}} {\ sqrt {6} +\ sqrt {2}}\). Entonces ya que\(\tan\;15^\circ = \cot\;75^\circ \) por el Teorema de la Cofunción, esto significa que\(\tan\;15^\circ = \frac{\sqrt{6} - \sqrt{2}}{\sqrt{6} + \sqrt{2}} \). A continuación describiremos otro método para encontrar los valores exactos de las funciones trigonométricas de\(15^\circ \). De hecho, se puede utilizar para encontrar los valores exactos para las funciones trigonométricas de\(\frac{\theta}{2} \) cuando se\(\theta \) conocen aquellos para, para cualquiera\(0^\circ < \theta < 90^\circ \). El método se ilustra en la Figura 1.3.5 y se describe a continuación.

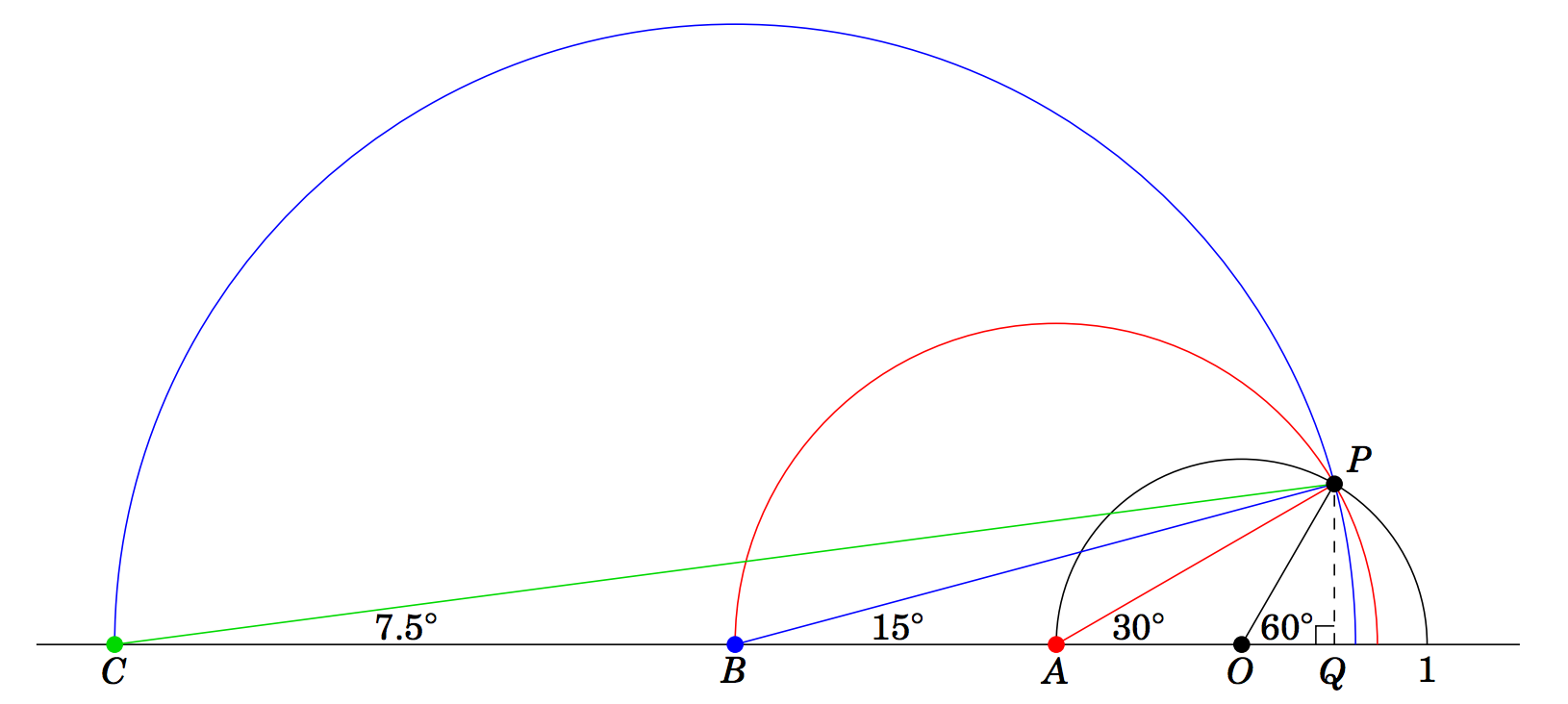
Figura 1.3.5

Dibuja un semicírculo de radio\(1 \) centrado en un punto\(O \) de una línea horizontal. Dejar\(P \) ser el punto en el semicírculo tal que\(\overline{OP} \) hace un ángulo de\(60^\circ \) con la línea horizontal, como en la Figura 1.3.5. Dibuja una línea recta hacia abajo desde\(P \) la línea horizontal en el punto\(Q \). Ahora crea un segundo semicírculo de la siguiente manera: Deja\(A \) ser el punto final izquierdo del primer semicírculo, luego dibuja un nuevo semicírculo centrado en\(A \) con radio igual a\(AP \). Luego crea un tercer semicírculo de la misma manera: Dejar\(B \) ser el punto final izquierdo del segundo semicírculo, luego dibujar un nuevo semicírculo centrado en\(B \) con radio igual a\(BP \).

Este procedimiento se puede continuar indefinidamente para crear más semicírculos. En general, se puede mostrar que el segmento de línea desde el centro del nuevo semicírculo\(P \) hace un ángulo con la línea horizontal igual a la mitad del ángulo desde el centro del semicírculo anterior a\(P \).

a) Explique por qué\(\angle\,PAQ=30^\circ \). (Pista: ¿Cuál es el suplemento\(60^\circ\)?)
b) Explicar por qué\(\angle\,PBQ=15^\circ \) y\(\angle\,PCQ=7.5^\circ \).
(c) Utilice la Figura 1.3.5 para encontrar los valores exactos de\(\sin\;15^\circ \),\(\cos\;15^\circ \), y\(\tan\;15^\circ \). (Pista: Para comenzar, necesitará usar\(\angle\,POQ = 60^\circ\) y\(OP = 1 \) encontrar las longitudes exactas de\(\overline{PQ} \) y\(\overline{OQ} \).)
(d) Utilice la Figura 1.3.5 para calcular el valor exacto de\(\tan\;7.5^\circ \).
(e) Utilizar el mismo método pero con un ángulo inicial de\(\angle\,POQ = 45^\circ \) para encontrar los valores exactos de\(\sin\;22.5^\circ \),\(\cos\;22.5^\circ \), y\(\tan\;22.5^\circ \).

1.3.25 Un fabricante necesita colocar diez rodamientos de bolas idénticos contra el lado interior de un contenedor circular de manera que cada rodamiento de bolas toque otros dos rodamientos de bolas, como en la imagen de la derecha. El radio (interno) del contenedor es\(4 \) cm.

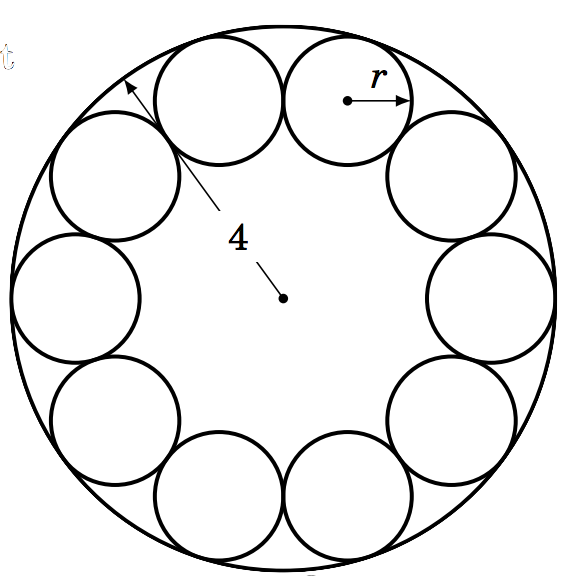
(a) Encontrar el radio común\(r \) de los rodamientos de bolas.
b) El fabricante necesita colocar un anillo circular\\ dentro del contenedor. ¿Cuál es el mayor radio posible (exterior) del anillo de tal manera que no esté en la parte superior\\ de los rodamientos de bolas y su base esté nivelada con la\\ base del contenedor?

1.3.26 Un círculo de radio\(1 \) se inscribe dentro de un polígono con ocho lados de igual longitud, llamado octágono regular. Es decir, cada uno de los ocho lados es tangente al círculo, como en la imagen de la derecha.

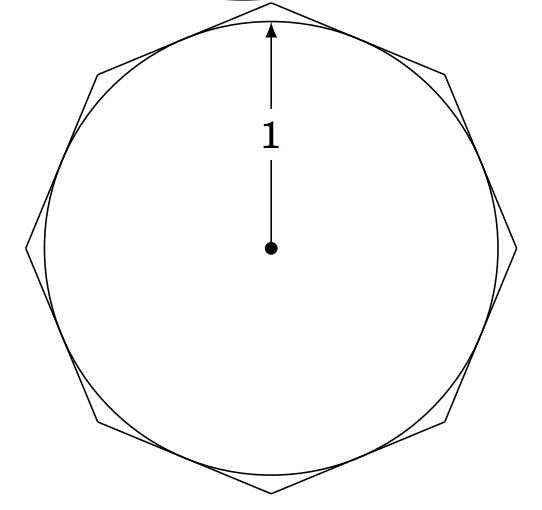
a) Calcular el área del octágono.
(b) Si aumentara el número de lados del polígono\\, ¿aumentaría o disminuiría el área dentro de él? ¿A qué número se acercaría el área, en su caso? Explique.
c) Inscribir un octágono regular dentro del mismo círculo. Es decir, dibujar un octágono regular de tal manera que cada uno de sus ocho vértice toque el círculo. Calcular el área de este octágono.

1.3.27 La imagen de la derecha muestra un cubo cuyos lados son de longitud\(a > 0 \).

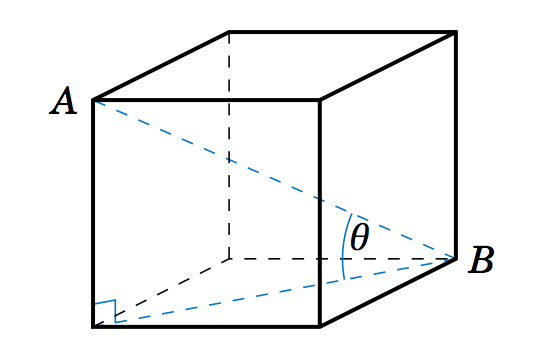
(a) Encontrar la longitud del segmento de línea diagonal\(\overline{AB} \).
(b) Encontrar el ángulo\(\theta \) que\(\overline{AB} \) hace con la base del cubo.

1.3.28 En la Figura 1.3.6, supongamos que\(\alpha \)\(\beta \),, y\(AD \) se conocen. Demostrar que:

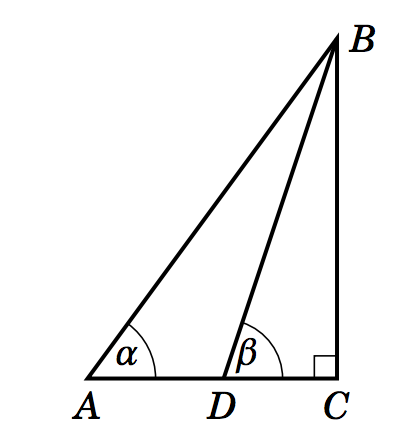
Figura 1.3.6

(a)\(BC ~=~ \dfrac{AD}{\cot\;\alpha - \cot\;\beta}\)
(b)\(AC ~=~ \dfrac{AD\;\cdot\;\tan\;\beta}{\tan\;\beta - \tan\;\alpha}\)
(c)\(BD ~=~ \dfrac{AD\;\cdot\;\sin\;\alpha}{\sin\;(\beta - \alpha)}\)
(Pista: ¿Cuál es la medida del ángulo\(\angle\,ABD\;\)?)

1.3.29 Las personas A y B están en la playa, sus ojos están\(5 \) pies y\(6 \) pies, respectivamente, sobre el nivel del mar. ¿Cuántas millas más lejos está el horizonte de la Persona B que el de la Persona A? (Nota:\(1 \) milla =\(5280\) pies)

---

1.4 Ejercicios

Para los Ejercicios 1-10, indicar en qué cuadrante o sobre qué eje se encuentra el ángulo dado.

1.4.1\(127^\circ\)

1.4.2\(-127^\circ\)

1.4.3\(313^\circ\)

1.4.4\(-313^\circ\)

1.4.5 \(-90^\circ\)

1.4.6\(621^\circ\)

1.4.7\(230^\circ\)

1.4.8\(2009^\circ\)

1.4.9\(1079^\circ\)

1.4.10\(-514^\circ\)

1.4.11 ¿En qué cuadrante (s) tienen el mismo signo el seno y el coseno?

1.4.12 ¿En qué cuadrante (s) tienen el signo opuesto el seno y el coseno?

1.4.13 ¿En qué cuadrante (s) tienen el mismo signo el seno y la tangente?

1.4.14 ¿En qué cuadrante (s) tienen el signo opuesto el seno y la tangente?

1.4.15 ¿En qué cuadrante (s) el coseno y la tangente tienen el mismo signo?

1.4.16 ¿En qué cuadrante (s) el coseno y la tangente tienen el signo opuesto?

Para Ejercicios 17-21, encuentra el ángulo de referencia para el ángulo dado.

1.4.17\(317^\circ\)

1.4.18\(63^\circ\)

1.4.19\(-126^\circ\)

1.4.20\(696^\circ\)

1.4.21\(275^\circ\)

Para los Ejercicios 22-26, encuentra los valores exactos de\(\sin\;\theta \) y\(\tan\;\theta \) cuándo\(\cos\;\theta \) tiene el valor indicado.

1.4.22\(\cos\;\theta = \frac{1}{2}\)

1.4.23\(\cos\;\theta = -\frac{1}{2}\)

1.4.24\(\cos\;\theta = 0\)

1.4.25\(\cos\;\theta = \frac{2}{5}\)

1.4.26\(\cos\;\theta = 1\)

Para los Ejercicios 27-31, encuentra los valores exactos de\(\cos\;\theta \) y\(\tan\;\theta \) cuándo\(\sin\;\theta \) tiene el valor indicado.

1.4.27\(\sin\;\theta = \frac{1}{2}\)

1.4.28\(\sin\;\theta = -\frac{1}{2}\)

1.4.29\(\sin\;\theta = 0\)

1.4.30\(\sin\;\theta = -\frac{2}{3}\)

1.4.31\(\sin\;\theta = 1\)

Para los Ejercicios 32-36, encuentra los valores exactos de\(\sin\;\theta \) y\(\cos\;\theta \) cuándo\(\tan\;\theta \) tiene el valor indicado.

1.4.32\(\tan\;\theta = \frac{1}{2}\)

1.4.33\(\tan\;\theta = -\frac{1}{2}\)

1.4.34\(\tan\;\theta = 0\)

1.4.35\(\tan\;\theta = \frac{5}{12}\)

1.4.36\(\tan\;\theta = 1\)

Para los Ejercicios 37-40, utilice la Tabla 1.3 para responder a las siguientes preguntas.

1.4.37 ¿Hace\(\sin\;180^\circ ~+~ \sin\;45^\circ ~=~ \sin\;225^\circ\;\)?

1.4.38 ¿Lo hace\(\tan\;300^\circ ~-~ \tan\;30^\circ ~=~ \tan\;270^\circ\;\)?

1.4.39 ¿Lo hace\(\cos\;180^\circ ~-~ \cos\;60^\circ ~=~ \cos\;120^\circ\;\)?

1.4.40 ¿Lo hace\(\cos\;240^\circ ~=~ (\cos\;120^\circ)^2 ~-~ (\sin\;120^\circ)^2 \;\)?

1.4.41 Expandir la Tabla 1.3 para incluir todos los múltiplos enteros de\(15^\circ \). Ver Ejemplo 1.10 en la Sección 1.2.

---

1.5 Ejercicios

1.5.1 Vamos\(\theta = 32^\circ \). Encontrar el ángulo entre\(0^\circ \) y\(360^\circ \) que es la

(a) reflexión de\(\theta \) alrededor del\(x\) eje -eje
(b) reflexión de\(\theta \) alrededor del\(y\) -eje
(c) reflexión de \(\theta \)alrededor del origen

1.5.2 Repetir Ejercicio 1 con\(\theta = 248^\circ \).

1.5.3 Repetir Ejercicio 1 con\(\theta = -248^\circ \).

1.5.4 Probamos las Ecuaciones 1.4-1.6 para cualquier ángulo\(\theta \) en QI. Imita esa prueba para demostrar que las fórmulas se mantienen para\(\theta \) en la QII.

1.5.5 Verificar las Ecuaciones 1.4-1.6 para\(\theta \) en los ejes de coordenadas, es decir\(\theta = 0^\circ \), para\(90^\circ \),,\(180^\circ \),\(270^\circ \).

1.5.6 En el Ejemplo 1.26 se utilizaron las fórmulas que implican\(\theta + 90^\circ \) para demostrar que las pendientes de las líneas perpendiculares son recíprocas negativas. Demostrar que este resultado también se puede probar usando las fórmulas que involucran\(\theta - 90^\circ \). (Pista: Solo se necesita modificar el último párrafo de ese ejemplo. )

Para los Ejercicios 7-14, encuentre todos los ángulos\(0^\circ \le \theta < 360^\circ \) que satisfagan la ecuación dada:

1.5.7\(\sin\;\theta = 0.4226\)

1.5.8\(\sin\;\theta = 0.1909\)

1.5.9 \(\cos\;\theta = 0.4226\)

1.5.10\(\sin\;\theta = 0\)

1.5.11\(\tan\;\theta = 0.7813\)

1.5.12\(\sin\;\theta = -0.6294\)

1.5.13\(\cos\;\theta = -0.9816\)

1.5.14\(\tan\;\theta = -9.514\)

1.5.15 En nuestra prueba del Teorema de Pitágoras en la Sección 1.2, afirmamos que en un triángulo rectángulo era\(\triangle\,ABC \) posible dibujar un segmento lineal\(\overline{CD} \) desde el vértice de ángulo recto\(C \) hasta un punto\(D \) sobre la hipotenusa\(\overline{AB} \) tal que\(\overline{CD} \perp \overline{AB} \). Usa la imagen de abajo para probar esa afirmación. (Pista: Observe cómo\(\triangle\,ABC \) se coloca en el plano de coordenadas\(xy\) -. ¿Cuál es la pendiente de la hipotenusa? ¿Cuál sería la pendiente de una línea perpendicular a ella? ) También, encontrar las\((x,y) \) coordenadas del punto\(D \) en términos de\(a \) y\(b \).

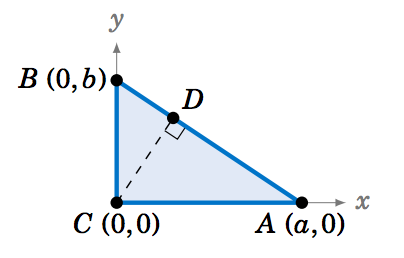
1.5.16 Se puede probar sin utilizar funciones trigonométricas que las pendientes de las líneas perpendiculares son recíprocas negativas. Dejar\(y = m_1{}x+b_1 \) y\(y = m_2{}x+b_2 \) ser líneas perpendiculares (con pendientes distintas de cero), como en la imagen de abajo. Usa la imagen para mostrar eso\(m_2 = -\frac{1}{m_1} \). (Pista: Piense en triángulos similares y la definición de pendiente.)

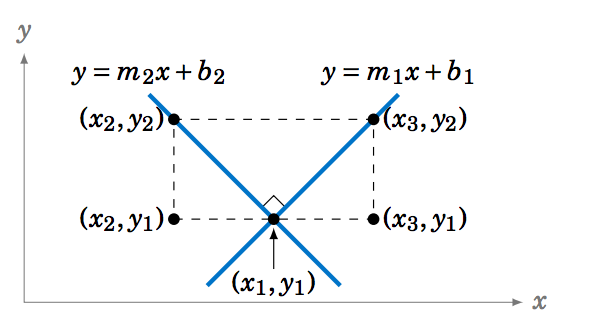
1.5.17 Probar las ecuaciones 1.19-1.21 mediante el uso de las ecuaciones 1.10-1.12 y 1.13-1.15.