2.1: La Ley de los Senos
- Page ID
- 113492
Si un triángulo tiene lados de longitudes\(a \),\(b \), y\(c \) opuestos a los ángulos\(A \)\(B \), y\(C \), respectivamente, entonces
\[\label{2.1} \dfrac{a}{\sin\;A} ~=~ \dfrac{b}{\sin\;B} ~=~ \dfrac{c}{\sin\;C} ~. \]
Tenga en cuenta que al tomar recíprocas, la ecuación\ ref {2.1} se puede escribir como
\ [\ label {2.2}
\ dfrac {\ sin\; A} {a} ~=~\ dfrac {\ sin\; B} {b} ~=~\ dfrac {\ sin\; C} {c} ~,
\ nonumber\]
y también se puede escribir como una colección de tres ecuaciones:
\ [\ label {2.3}
\ dfrac {a} {b} ~=~\ dfrac {\ sin\; A} {\ sin\; B} ~~,\ quad\ dfrac {a} {c} ~=~\ dfrac {\ sin\; A} {\ sin\; C} ~~,\ quad
\ dfrac {b} {c} ~=~ d=~ frac {\ sin\; B} {\ sin\; C}
\ nonumber\]
Otra forma de afirmar la Ley de los Sinos es: Los lados de un triángulo son proporcionales a los senos de sus ángulos opuestos.
Para probar la Ley de los Sines, deja\(\triangle\,ABC \) ser un triángulo oblicuo. Entonces\(\angle \,ABC \) puede ser agudo, como en la Figura\(\PageIndex{1}\) (a), o puede ser obtuso, como en la Figura\(\PageIndex{1}\) (b). En cada caso, dibuja la altitud desde el vértice\(C \) a un lado\(\overline{AB} \). En la Figura\(\PageIndex{1}\) (a) la altitud se encuentra dentro del triángulo, mientras que en la Figura\(\PageIndex{1}\) (b) la altitud se encuentra fuera del triángulo.
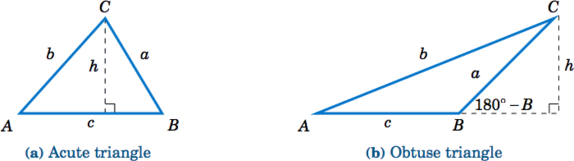
Dejar\(h \) ser la altura de la altitud. Por cada triángulo en la Figura\(\PageIndex{1}\), vemos que
\[ \dfrac{h}{b} ~=~ \sin\;A\label{2.4} \]
y
\[ \dfrac{h}{a} ~=~ \sin\;B\label{2.5} \]
en la Figura\(\PageIndex{1}\) (b),\(\dfrac{h}{a} = \sin\;(180^\circ - B) = \sin\;B \) por la Ecuación (1.19) en la Sección 1.5). Así, resolviendo para\(h \) en la Ecuación\ ref {2.5} y sustituyéndolo en Ecuación\ ref {2.4} da
\[\dfrac{a\;\sin\;B}{b} ~=~ \sin\;A ~,\label{2.6} \]
y así poniendo\(a \) y\(A \) en el lado izquierdo y\(b \) y\(B \) en el lado derecho, conseguimos
\[\dfrac{a}{\sin\;A} ~=~ \dfrac{b}{\sin\;B} ~.\label{2.7} \]
Por un argumento similar, dibujar la altitud de\(A \) a\(\overline{BC} \) da
\[\label{2.8} \dfrac{b}{\sin\;B} ~=~ \dfrac{c}{\sin\;C} ~, \]
así que juntar las dos últimas ecuaciones demuestra el teorema.
\(\square\)
Obsérvese que no probamos la Ley de los Senos para los triángulos rectos, ya que resulta (ver Ejercicio 12) ser trivialmente cierta para ese caso.
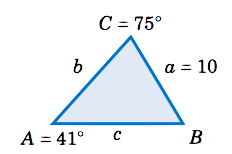
Resolver el triángulo\(\triangle\,ABC \) dado\(a = 10 \)\(A =41^\circ \),, y\(C = 75^\circ \).
Solución
Podemos encontrar el tercer ángulo restando los otros dos ángulos\(180^\circ \), luego usar la ley de los senos para encontrar los dos lados desconocidos. En este ejemplo necesitamos encontrar\(B \),\(b \), y\(c \). Primero, vemos que
\ [B ~=~ 180^\ circ ~-~ A ~-~ C ~=~ 180^\ circ ~-~ 41^\ circ ~-~ 75^\ circ\ quad\ Rightarrow\ quad
\ en caja {B ~=~ 64^\ circ} ~. \ nonumber\]
Entonces por la Ley de los Sines tenemos
\ [\ begin {align}
\ dfrac {b} {\ sin\; B} ~&=~\ dfrac {a} {\ sin\; A}\ quad&\ Rightarrow\ quad b ~&=~\ dfrac {a\;\ sin\; B} {\ sin\; A}
~&=~\ dfrac {10\;\ sin\; 64^\ c} {\ sin\; 41^\ circ}\ quad&\ Rightarrow\ quad\ en caja {b ~=~ 13.7}
~, ~\ texto {y}\\ [4pt]\ nonumber
\ dfrac {c} {\ sin\; C} ~&=~\ dfrac {a} {\ sin\; A}\ quad&\ Rightarrow\ quad c ~&=~\ dfrac {a\;\ sin\; C} {\ sin\; A}
~&=~\ dfrac {10\;\ sin\; 75^\ circ} {\ sin\; 41^\ circ}\ quad&\ Rightarrow\ quad\ boxed {c ~=~ 14.7} ~.
\ end {align}\ nonumber\]
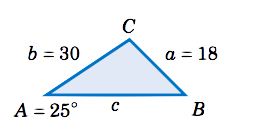
Resolver el triángulo\(\triangle\,ABC \) dado\(a = 18 \)\(A = 25^\circ \),, y\(b = 30 \).
Solución
En este ejemplo conocemos el lado\(a \) y su ángulo opuesto\(A \), y conocemos el lado\(b \). Podemos usar la Ley de los Sinos para encontrar el otro ángulo opuesto\(B \), luego encontrar el tercer ángulo\(C \) restando\(A \) y\(B \) de\(180^\circ \), luego usar la ley de los senos para encontrar el tercer lado\(c \). Por la Ley de Sines, tenemos
\ [\ dfrac {\ sin\; B} {b} ~=~\ dfrac {\ sin\; A} {a}\ quad\ Rightarrow\ quad\ sin\; B ~=~\ dfrac {b\;\ sin\; A} {a} ~=~
\ dfrac {30\;\ sin\; 25^\ circ} {18}\\ derecha Tarrow\ quad\ sin\; B ~=~ 0.7044 ~. \ nonumber\]
Usando el botón\(\fbox{\(\sin^{-1}\)}\) en una calculadora da\(B = 44.8^\circ \). No obstante, recordemos de la Sección 1.5 que\(\sin\;(180^\circ - B) = \sin\;B \). Entonces hay una segunda solución posible para\(B \), a saber\(180^\circ - 44.8^\circ = 135.2^\circ \). Así, tenemos que resolver dos veces para\(C \) y\(c \): una por\(B = 44.8^\circ \) y una para\(B = 135.2^\circ\):
\ [\ begin {array} {c|c}
\ en caja {B = 44.8^\ circ} &\ en caja {B = 135.2^\ circ}\\
C = 180^\ circ - A - B = 180^\ circ - 25^\ circ - 44.8^\ circ = 110.2^\ circ &
C = 180^\ circ - A - B = 180^\ circ - 25^\ circ - 135.2^\ circ = 19.8^\ circ\
\ dfrac {c} {\ sin\; C} =\ dfrac {a} {\ sin\; A} ~\ Derecha~ c =\ dfrac {a\;\ sin\; C} {\ sin\; A}
=\ dfrac {18\;\ sin\; 110.2^\ circ} {\ sin\; 25^\ circ} &
\ dfrac {c} {\ sin\; C} =\ dfrac {a} {\ sin\; A} ~\ Derecha~ c =\ dfrac {a\;\ sin\; C} {\ sin\; A}
=\ dfrac {18\;\ sin\; 19.8^\ circ} {\ sin\; 25^\ circ}\\
\ Derecha~ c = 40 &\ Rightarrow ~ c = 14.4
\ end {array}\ nonumber\]
De ahí que\(\fbox{\(B = 44.8^\circ \)\(C = 110.2^\circ \),,\(c = 40\)}\) y\(\fbox{\(B = 135.2^\circ \)\(C = 19.8^\circ \),,\(c = 14.4\)}\) son los dos conjuntos posibles de soluciones. Esto significa que hay dos triángulos posibles, como se muestra en la Figura\(\PageIndex{2}\).

En Ejemplo\(\PageIndex{2}\) vimos lo que se conoce como el caso ambiguo. Es decir, puede haber más de una solución. También es posible que haya exactamente una solución o ninguna solución en absoluto.
Resolver el triángulo\(\triangle\,ABC \) dado\(a = 5 \)\(A = 30^\circ \),, y\(b = 12 \).
Solución
Por la Ley de Sines, tenemos
\ [\ dfrac {\ sin\; B} {b} ~=~\ dfrac {\ sin\; A} {a}\ cuádruple\ fila derecha\ cuádruple\ sin\; B ~=~\ dfrac {b\;\ sin\; A} {a} ~=~
\ dfrac {12\;\ sin\; 30^\ circ} {5}\ derecha tarrow\ quad\ sin\; B ~=~ 1.2 ~,\ nonumber\]
lo cual es imposible ya que\(| \sin\;B | \le 1 \) para cualquier ángulo\(B \). Así, la hay\(\fbox{no solution}\).
Hay una manera de determinar cuántas soluciones tiene un triángulo en el Caso 2. Para un triángulo\(\triangle\,ABC \), supongamos que conocemos los lados\(a \) y\(b \) y el ángulo\(A \). Dibuja el ángulo\(A\) y el lado\(b \), e imagina que el lado\(a \) está unido en el vértice en\(C \) para que pueda “balancearse” libremente, como lo indica el arco discontinuo en la Figura\(\PageIndex{3}\) a continuación.
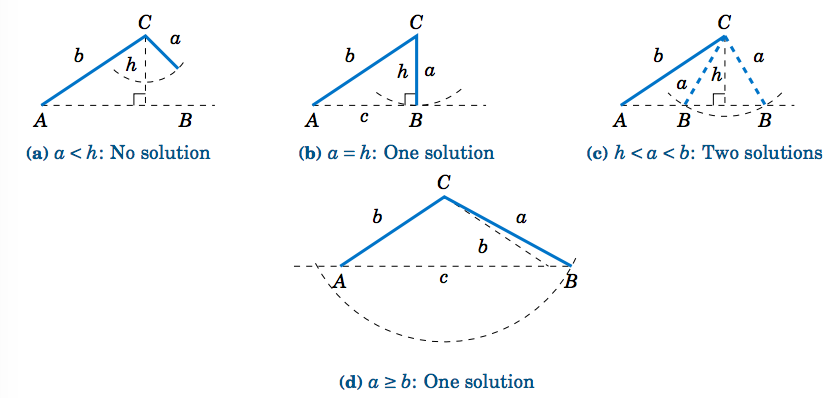
Si\(A \) es agudo, entonces la altitud de\(C \) a\(\overline{AB} \) tiene altura\(h = b\;\sin\;A \). Como podemos ver en la Figura\(\PageIndex{3}\) (a) - (c), no hay solución cuando\(a < h \) (este fue el caso en el Ejemplo 2.3); hay exactamente una solución -es decir, un triángulo rectángulo- cuándo\(a = h\); y hay dos soluciones cuando\(h < a < b \) (como fue el caso en el Ejemplo 2.2). Cuando sólo\(a \ge b \) hay una solución, aunque de la Figura\(\PageIndex{3}\) (d) se desprende que puede haber dos soluciones, ya que el arco discontinuo cruza la línea horizontal en dos puntos. Sin embargo, el punto de intersección a la izquierda de\(A \) en la Figura\(\PageIndex{3}\) (d) no se puede utilizar para determinar\(B \), ya que eso haría\(A \) un ángulo obtuso, y asumimos que\(A \) era agudo.
Si no\(A \) es agudo (\(A \)es decir, es obtuso o un ángulo recto), entonces la situación es más simple: no hay solución si\(a \le b \), y hay exactamente una solución si\(a > b \) (ver Figura\(\PageIndex{4}\)).
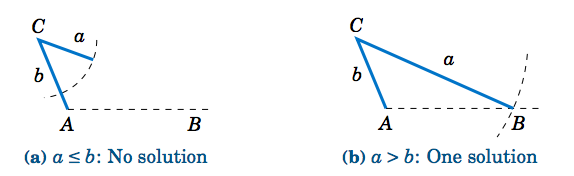
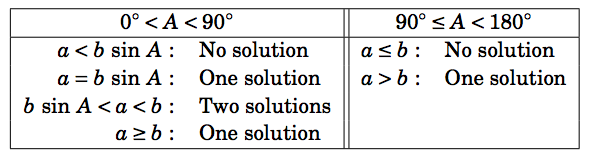
El Cuadro 2.1 resume el caso ambiguo de resolver\(\triangle\,ABC \) cuando se da\(a \),\(A \), y\(b \). Por supuesto, las letras pueden intercambiarse, por ejemplo, reemplazar\(a \) y\(A \) por\(c\) y\(C \), etc.
Cuadro 2.1 Resumen del caso ambiguo
Hay una interesante consecuencia geométrica de la Ley de los Sines. Recordemos de la Sección 1.1 que en un triángulo rectángulo la hipotenusa es el lado más grande. Dado que un ángulo recto es el ángulo más grande en un triángulo rectángulo, esto significa que el lado más grande es opuesto al ángulo más grande. Lo que hace la Ley de Sines es generalizar esto a cualquier triángulo:
En cualquier triángulo, el lado más grande es opuesto al ángulo más grande.
Para probarlo, deja\(C \) ser el ángulo más grande en un triángulo\(\triangle\,ABC \). Si\(C = 90^\circ \) entonces ya sabemos que su lado opuesto\(c \) es el lado más grande. Entonces solo tenemos que probar el resultado para cuándo\(C \) es agudo y para cuándo\(C \) es obtuso. En ambos casos, tenemos\(A \le C \) y\(B \le C \). Primero mostraremos eso\(\sin\;A \le \sin\;C \) y\(\sin\;B \le \sin\;C \).
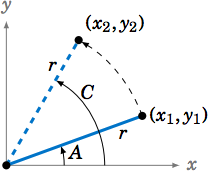
Si\(C \) es agudo, entonces\(A \) y también\(B \) son agudos. Ya que\(A \le C \), imaginemos que\(A \) está en posición estándar en el plano\(xy\) -coordenada y que giramos el lado terminal de\(A \) sentido antihorario al lado terminal del ángulo mayor\(C \), como en la Figura\(\PageIndex{5}\). Si elegimos puntos\((x_{1},y_{1}) \) y\((x_{2},y_{2}) \) en los lados terminales de\(A \) y\(C \), respectivamente, de manera que su distancia al origen sea el mismo número\(r \), entonces vemos en la imagen que\(y_{1} \le y_{2} \), y por lo tanto
\ [\ sin\; A ~=~\ dfrac {y_ {1}} {r} ~\ le~\ dfrac {y_ {2}} {r} ~=~\ sin\; C ~.
\ nonumber\]
Por un argumento similar,\(B \le C \) implica que\(\sin\;B \le \sin\;C \). Así,\(\sin\;A \le \sin\;C\) y\(\sin\;B \le \sin\;C \) cuando\(C \) es agudo. Ahora vamos a demostrar que estas desigualdades se mantienen cuando\(C \) es obtuso.
Si\(C \) es obtuso, entonces\(180^\circ - C \) es agudo, como son\(A \) y\(B \). Si\(A > 180^\circ -C\) entonces\(A + C > 180^\circ \), lo cual es imposible. Por lo tanto, debemos tener\(A \le 180^\circ - C \). De igual manera,\(B \le 180^\circ - C \). Entonces por lo que mostramos arriba para ángulos agudos, lo sabemos\(\sin\;A \le \sin\;(180^\circ - C) \) y\(\sin\;B \le \sin\;(180^\circ - C) \). Pero sabemos por la Sección 1.5 que\(\sin\;C = \sin\;(180^\circ - C) \). De ahí,\(\sin\;A \le \sin\;C\) y\(\sin\;B \le \sin\;C \) cuándo\(C \) es obtuso.
Así,\(\sin\;A \le \sin\;C \) si\(C \) es agudo u obtuso, entonces por la Ley de los Sinos tenemos
\ [\ dfrac {a} {c} ~=~\ dfrac {\ sin\; A} {\ sin\; C} ~\ le~\ dfrac {\ sin\; C} {\ sin\; C} ~=~ 1\ quad\ Rightarrow
\ quad\ dfrac {a} {c} ~\ le~ 1\ quad\ Letarrow\ quad a ~\ ~ c ~.
\ nonumber\]
Por un argumento similar,\(b \le c \). Así,\(a \le c \) y\(b \le c \), es decir,\(c \) es el lado más grande.
\(\square\)


