2.2: La Ley de los Cosinos
- Page ID
- 113487
Ahora discutiremos cómo resolver un triángulo en el Caso 3: dos lados y el ángulo entre ellos. Primero, veamos qué pasa cuando tratamos de usar la Ley de los Senos para este caso.
Resolver el triángulo\(\triangle\,ABC \) dado\(A = 30^\circ \)\(b = 4 \),, y\(c = 5 \).

Solución
Usando la Ley de Sines, tenemos
\[\nonumber \dfrac{a}{\sin\;30^\circ} ~=~ \dfrac{4}{\sin\;B} ~=~ \dfrac{5}{\sin\;C} ~, \nonumber \]
donde cada una de las ecuaciones tiene dos partes desconocidas, haciendo imposible resolver el problema. Por ejemplo, para resolver por\(a \) podríamos usar la ecuación
\[\dfrac{4}{\sin\;B} = \dfrac{5}{\sin\;C} \nonumber \]
para resolver\(\sin\;B \) en términos de\(\sin\;C \) y sustituirlo en la ecuación
\[\dfrac{a}{\sin\;30^\circ} = \dfrac{4}{\sin\;B}. \nonumber \]
Pero eso solo resultaría en la ecuación
\[\dfrac{a}{\sin\;30^\circ} = \dfrac{5}{\sin\;C} ,\nonumber \]
que ya conocíamos y que todavía tiene dos incógnitas! Por lo tanto, este problema no puede resolverse utilizando la Ley de los Sines.
Para resolver el triángulo en el ejemplo anterior, podemos usar la Ley de Cosinos:
Si un triángulo tiene lados de longitudes\(a \),\(b \), y\(c \) opuestos a los ángulos\(A \)\(B \), y\(C \), respectivamente, entonces
\ [\ begin {align}
a^2 ~ &= b^2 + c^2 - 2bc\;\ cos\; A ~,\ label {2.9}\\ [4pt]
b^2 ~ &= c^2 + a^2 - 2ca\;\ cos\; B ~,\ etiqueta {2.10}\\ [4pt]
c^2 ~ &= a^2 + b^2 - 2ab\;\ cos\; C ~. \ label {2.11}\\ [4pt]
\ end {align}\ nonumber\]
Para probar la Ley de Cosinos, deje\(\triangle\,ABC \) ser un triángulo oblicuo. Entonces\(\triangle\,ABC \) puede ser agudo, como en la Figura\(\PageIndex{1a}\), o puede ser obtuso, como en Figura\(\PageIndex{1b}\). En cada caso, dibuja la altitud desde el vértice\(C \) a un lado\(\overline{AB} \). En la Figura\(\PageIndex{1a}\), la altitud\(\overline{AB} \) se divide en dos segmentos de línea con longitudes\(x \) y\(c-x \), mientras que en\(\PageIndex{1b}\) la Figura la altitud extiende el lado\(\overline{AB} \) por una distancia\(x \). Dejar\(h \) ser la altura de la altitud.
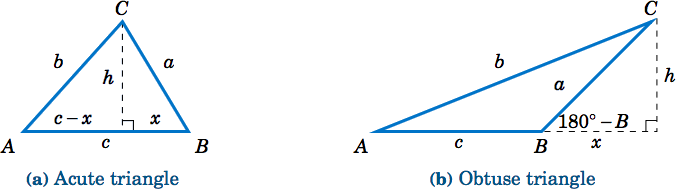
Por cada triángulo en la Figura\(\PageIndex{1}\), vemos por el Teorema de Pitágoras que
\[h^2 ~=~ a^2 ~-~ x^2\label{2.12} \]
y de igual manera para el triángulo agudo en la Figura\(\PageIndex{1a}\) vemos que
\[b^2 ~=~ h^2 ~+~ (c-x)^2 ~.\label{2.13} \]
Así, sustituyendo la expresión para\(h^2 \) en la Ecuación\ ref {2.12} en Ecuación\ ref {2.13} da
\ [\ begin {align*} b^2 ~&=~ a^2 ~-~ x^2 ~+~ (c-x) ^2\ nonumber\\
&=~ a^2 ~-~ x^2 ~+~ c^2 ~-~ 2cx ~+~ x^2\ nonumber\\
&=~ a^2 ~+~ c^2 ~-~ 2cx ~. \ nonumber\\\ end {align*}\ nonumber\]
Pero vemos de Figura\(\PageIndex{1a}\) que\(x = a\;\cos\;B \), así
\[ b^2 ~=~ a^2 ~+~ c^2 ~-~ 2ca\;\cos\;B ~.\label{2.14} \]
Y para el triángulo obtuso en Figura\(\PageIndex{1b}\) vemos que
\[ b^2 ~=~ h^2 ~+~ (c+x)^2 ~.\label{2.15} \]
Así, sustituyendo la expresión para\(h^2 \) en la Ecuación\ ref {2.12} en Ecuación\ ref {2.15} da
\ [\ begin {align*} b^2 ~&=~ a^2 ~-~ x^2 ~+~ (c+x) ^2\ nonumber\\
&=~ a^2 ~-~ x^2 ~+~ c^2 ~+~ 2cx ~+~ x^2\ nonumber\\
&=~ a^2 ~+~ c^2 ~+~ 2cx ~. \ nonumber\\\ end {align*}\ nonumber\]
Pero vemos a partir de la Figura\(\PageIndex{1a}\) eso\(x = a\;\cos\;(180^\circ - B) \), y sabemos por la Sección 1.5 que\(\cos\;(180^\circ - B) = -\cos\;B \). Así,\(x = -a\;\cos\;B\) y así
\[ b^2 ~=~ a^2 ~+~ c^2 ~-~ 2ca\;\cos\;B ~.\label{2.16} \]
Así que para los triángulos tanto agudos como obtusos hemos probado la Ecuación\ ref {2.10} en la Ley de los Cosinos. Observe que la prueba fue para\(B \) aguda y obtusa. Por argumentos similares a favor\(A \) y\(C\) obtenemos las otras dos fórmulas.
\(\square\)
Tenga en cuenta que no probamos la Ley de Cosinos para los triángulos rectos, ya que resulta (ver Ejercicio 15) que las tres fórmulas reducen al Teorema de Pitágoras para ese caso. La Ley de Cosinos puede ser vista como una generalización del Teorema de Pitágoras.
También, fíjese que basta con recordar solo una de las tres Ecuaciones\ ref {2.9} -\ ref {2.11}, ya que las otras dos se pueden obtener “ciclando” a través de las letras\(a \),\(b \), y\(c \). Es decir, sustituir\(a \) por\(b \), sustituir\(b \) por\(c \), y sustituir\(c \) por\(a \) (así mismo para las letras mayúsculas). Un ciclo te dará la segunda fórmula, y otro ciclo te dará el tercero.
El ángulo entre dos lados de un triángulo a menudo se llama el ángulo incluido. Observe en la Ley de Cosinos que si se conocen dos lados y su ángulo incluido (e.g.\(b \)\(c \),, y\(A\)), entonces tenemos una fórmula para el cuadrado del tercer lado. Ahora vamos a resolver el triángulo de Ejemplo\(\PageIndex{2}\).
Resolver el triángulo\(\triangle\,ABC \) dado\(A = 30^\circ \)\(b = 4 \),, y\(c = 5 \).
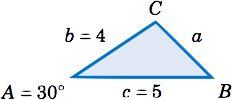
Solución
Vamos a utilizar la Ley de Cosinos para encontrar\(a \), utilizarla de nuevo para encontrar\(B \), luego usar\(C = 180^\circ - A - B \). Primero, tenemos
\ [\ nonumber\ begin {align*}
a^2 ~ &= ~ b^2 ~ &+ ~ c^2 ~ &- ~ 2bc\;\ cos\; A\\\ nonumber
&= ~ 4^2 ~ &+ ~ 5^2 ~ &- ~ 2 (4) (5)\;\ cos\; 30^\ circ ~=~ 6.36\ quad\ Rightarrow\ quad
\ en caja {a ~=~ 2.52} ~. \\
\ final {alinear*}\ nonumber\]
Ahora usamos la fórmula\(b^2 \) para encontrar\(B\):
\ [\ nonumber\ begin {align*}
b^2 ~ = ~ c^2 ~ + ~ a^2 ~ - ~ 2ca\;\ cos\; B\ quad&\ Rightarrow
\ quad\ cos\; B ~=~\ dfrac {c^2 ~ + ~ a^2 ~-~ b^2} {2ca}\\ nonumber
&\ Rightarrow\\ cos\; B ~=~\ dfrac {5^2 ~ + ~ (2.52) ^2 ~-~ 4^2} {2 (5) (2.52)} ~=~ 0.6091\\\ nonumber
&\ Rightarrow\ quad\ boxed {B ~=~ 52.5^\ circ}\\
\ end {align*}\ nonumber\]
Así,\(C = 180^\circ - A - B = 180^\circ - 30^\circ - 52.5^\circ \Rightarrow \fbox{\(C = 97.5^\circ \; \)}\).
Observe en Ejemplo\(\PageIndex{2}\) que solo había una solución. Para el Caso 3 esto siempre será cierto: cuando se le den dos lados y su ángulo incluido, el triángulo tendrá exactamente una solución. La razón es simple: al unir dos segmentos de línea en un vértice común para formar un ángulo, hay exactamente una manera de conectar sus extremos libres con un tercer segmento de línea, independientemente del tamaño del ángulo.
Quizás te estés preguntando por qué usamos la Ley de Cosinos por segunda vez en Ejemplo\(\PageIndex{2}\), para encontrar el ángulo\(B \). ¿Por qué no usar la Ley de Sines, que tiene una fórmula más simple? La razón es que el uso de la función coseno elimina cualquier ambigüedad: si el coseno es positivo entonces el ángulo es agudo, y si el coseno es negativo entonces el ángulo es obtuso. Esto contrasta con el uso de la función sinusoidal; como vimos en la Sección 2.1, tanto un ángulo agudo como su suplemento obtuso tienen el mismo seno positivo.
Para ver esto, supongamos que habíamos usado la Ley de los Sinos para encontrar\(B \) en Ejemplo\(\PageIndex{2}\):
\ [\ sin\; B ~=~\ dfrac {b\;\ sin\; A} {a} ~=~\ dfrac {4\;\ sin\; 30^\ circ} {2.52} ~=~ 0.7937
\ quad\ Rightarrow\ quad B ~=~ 52.5^\ circ ~\ text {o} ~ 127.5^\ circ
\ nonúmero\]
¿Cómo sabríamos cuál es la respuesta correcta? No pudimos descartar de inmediato\(B = 127.5^\circ \) como demasiado grande, ya que haría\(A + B = 157.5^\circ < 180^\circ \) y así\(C = 22.5^\circ \), lo que parece que podría ser una solución válida. Sin embargo, esta solución es imposible. ¿Por qué? Porque el lado más grande del triángulo es\(c = 5 \), que (como aprendimos en la Sección 2.1) significa que\(C \) tiene que ser el ángulo más grande. Pero no\(C = 22.5^\circ \) sería el ángulo más grande en esta solución, y de ahí tenemos una contradicción.
Queda por resolver un triángulo en el Caso 4, es decir dado tres lados. Ahora veremos cómo utilizar la Ley de Cosinos para ese caso.
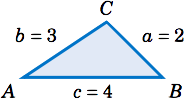
Resolver el triángulo\(\triangle\,ABC \) dado\(a = 2 \)\(b = 3 \),, y\(c = 4 \).
Solución
Vamos a utilizar la Ley de Cosinos para encontrar\(B \) y\(C \), después, utilizar\(A = 180^\circ - B - C \). Primero, usamos la fórmula\(b^2 \) para encontrar\(B\):
\ [\ nonumber\ begin {align*}
b^2 ~ = ~ c^2 ~ + ~ a^2 ~ - ~ 2ca\;\ cos\; B\ quad&\ Rightarrow
\ quad\ cos\; B ~=~\ dfrac {c^2 ~ + ~ a^2 ~-~ b^2} {2ca}\\ nonumber
&\ Rightarrow\\ cos\; B ~=~\ dfrac {4^2 ~ + ~ 2^2 ~-~ 3^2} {2 (4) (2)} ~=~ 0.6875\\\ nonumber
& amp;\ Rightarrow\ quad\ boxed {B ~=~ 46.6^\ circ}\\
\ end {align*}\ nonumber\]
Ahora usamos la fórmula\(c^2 \) para encontrar\(C\):
\ [\ nonumber\ begin {align*}
c^2 ~ = ~ a^2 ~ + ~ b^2 ~ - ~ 2ab\;\ cos\; C\ quad&\ Rightarrow\ quad
\ cos\; C ~=~\ dfrac {a^2 ~ + ~ b^2 ~-~ c^2} {2ab}\\ nonumber
&\ Rightarrow\\ cos\; C ~=~\ dfrac {2^2 ~ + ~ 3^2 ~-~ 4^2} {2 (2) (3)} ~=~ -0.25\\\ nonumber
& amp;\ Rightarrow\ quad\ boxed {C ~=~ 104.5^\ circ}\\
\ end {align*}\ nonumber\]
Así,\(A = 180^\circ - B - C = 180^\circ - 46.6^\circ - 104.5^\circ \Rightarrow \boxed{A = 28.9^\circ}\; \).
Puede parecer que siempre hay una solución en el Caso 4 (dadas las tres caras), pero eso no es cierto, como muestra el siguiente ejemplo.
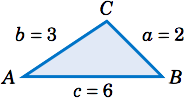
Resolver el triángulo\(\triangle\,ABC \) dado\(a = 2 \)\(b = 3 \),, y\(c = 6 \).
Solución
Si tratamos ciegamente de usar la Ley de Cosinos para encontrar\(A \), obtenemos
\ [a^2 ~ = ~ b^2 ~ + ~ c^2 ~ - ~ 2bc\;\ cos\; A\ quad\ Rightarrow\ quad\ cos\; A ~=~
\ dfrac {b^2 ~ + ~ c^2 ~-~ a^2} {2bc} ~=~\ dfrac {3^2 ~ + ~ 6^2 ~-~ 2^2} {2 (3) (6)} ~=~ 1.139 ~,
\ nonumber\]
lo cual es imposible desde entonces\(| \cos\;A | \le 1 \). Así, la hay\(\fbox{no solution}\).
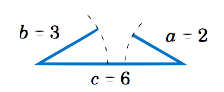
Podríamos habernos ahorrado algún esfuerzo al reconocer que la longitud de uno de los lados (\(c=6\)) es mayor que las sumas de las longitudes de los lados restantes (\(a=2 \)y\(b=3\)), lo cual (como muestra la imagen de abajo) es imposible en un triángulo.
La Ley de los Cosinos también puede ser utilizada para resolver triángulos en el Caso 2 (dos lados y un ángulo opuesto), aunque es menos utilizada para ese propósito que la Ley de los Sinos. El siguiente ejemplo da una idea de cómo hacer esto.
Resolver el triángulo\(\triangle\,ABC \) dado\(a = 18 \)\(A = 25^\circ \),, y\(b = 30 \).
Solución
En el Ejemplo 2.2 de la Sección 2.1 se utilizó la Ley de los Sinos para mostrar que existen dos conjuntos de soluciones para este triángulo:\(B = 44.8^\circ \),\(C = 110.2^\circ \),\(c = 40 \) y\(B = 135.2^\circ \),\(C = 19.8^\circ \),\(c = 14.4 \). Para resolver esto usando la Ley de Cosinos, primero encuentra\(c \) usando la fórmula para\(a^2\):
\ [\ nonumber\ begin {alinear*}
a^2 ~ = ~ b^2 ~ + ~ c^2 ~ - ~ 2bc\;\ cos\; A\ quad&\ Rightarrow\ quad
18^2 = ~ 30^2 ~ + ~ c^2 ~ - ~ 2 (30) c\;\ cos\; 25^\ circ\\ nonumber
&\ Rightarrow\ c^2 ~-~ 54.38\, c ~+~ 576 ~ = ~ 0 ~,
\ final {alinear*}\ nonumber\]
que es una ecuación cuadrática en\(c \), entonces sabemos que puede tener cero, una o dos raíces reales (correspondientes al número de soluciones en el Caso 2). Por la fórmula cuadrática, tenemos
\ [c ~=~\ dfrac {54.38 ~\ pm~\ sqrt {(54.38) ^2 ~-~ 4 (1) (576)}} {2 (1)} ~=~ 40 ~~\ texto {o} ~~ 14.4 ~.
\ nonumber\]
Tenga en cuenta que estos son los mismos valores para los\(c \) que encontramos antes. Para\(c=40 \) nosotros conseguimos
\ [\ cos\; B ~=~\ dfrac {c^2 ~ + ~ a^2 ~-~ b^2} {2ca} ~=~
\ dfrac {40^2 ~ + ~ 18^2 ~-~ 30^2} {2 (40) (18)} ~=~ 0.7111
\ cuádruple\ fila derecha\ cuádruple B ~=~ 44.7^\ circ\ Rightarrow\ quad C ~=~ 110.3^\ circ ~,
\ nonumber\]
que está cerca de lo que encontramos antes (la pequeña diferencia se debe a diferentes redondeos). El otro conjunto de soluciones se puede obtener de manera similar.
Al igual que la Ley de los Sinos, la Ley de los Cosinos puede ser utilizada para probar algunos hechos geométricos, como en el siguiente ejemplo.
Usa la Ley de Cosinos para probar que la suma de los cuadrados de las diagonales de cualquier paralelogramo es igual a la suma de los cuadrados de los lados.
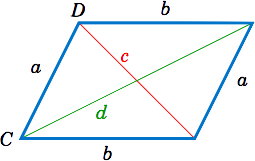
Solución:
Dejar\(a \) y\(b \) ser las longitudes de los lados, y dejar que las diagonales opuestas a los ángulos\(C \) y\(D \) tengan longitudes\(c \) y\(d \), respectivamente, como en la Figura\(\PageIndex{2}\). Entonces tenemos que demostrar que
\[c^2 ~+~ d^2 ~=~ a^2 ~+~ b^2 ~+~ a^2 ~+~ b^2 ~=~ 2\,( a^2 ~+~ b^2 ) ~.\nonumber \]
Por la Ley de Cosines, sabemos que
\ [\ nonumber\ begin {align*}
c^2 ~ &= ~ a^2 ~ + ~ b^2 ~ - ~ 2ab\;\ cos\; C ~, ~\ text {y}\\\ nonumber
d^2 ~ &= ~ a^2 ~ + ~ b^2 ~ - ~ 2ab\;\ cos\; D ~.\\ no fin {align*}\ umber\]
Por propiedades de paralelogramos, sabemos que\(D = 180^\circ - C \), entonces
\[\nonumber \begin{align*} d^2 ~ &= ~ a^2 ~ + ~ b^2 ~ - ~ 2ab\;\cos\;(180^\circ - C)\\ \nonumber &=~ a^2 ~ + ~ b^2 ~ + ~ 2ab\;\cos\;C ~, \\ \end{align*} \nonumber \]
ya que\(\;\cos\;(180^\circ - C) = -\cos\;C \). Por lo tanto,
\ [\ nonumber\ begin {alinear*} c^2 ~+~ d^2 ~&=~ a^2 ~ + ~ b^2 ~ - ~ 2ab\;\ cos\; C ~+~ a^2 ~ + ~ b^2 ~ + ~ 2ab\;\ cos\; C\\ nonumber
&=~ 2\, (a^2 ~+~ b^2) ~. \ quad\\\ final {alinear*}\ nonumber\]


