2.3: La Ley de las Tangentes
- Page ID
- 113486
Hemos mostrado cómo resolver un triángulo en los cuatro casos discutidos al inicio de este capítulo. Una alternativa a la Ley de Cosinos para el Caso 3 (dos lados y el ángulo incluido) es la Ley de Tangentes:
Si un triángulo tiene lados de longitudes\(a \),\(b \), y\(c \) opuestos a los ángulos\(A \)\(B \), y\(C \), respectivamente, entonces
\ [\ begin {align}
\ label {2.17}\ frac {a-b} {a+b} ~&=~
\ frac {\ tan\;\ frac {1} {2} (A-B)} {\ tan\;\ frac {1} {2} (A+B)} ~,\\\ etiqueta {2.18}
\ frac {b-c} {b+c} ~&=~
\ frac {\ tan\;\ frac {1} {2} (B-C)} {\ tan\;\ frac {1} {2} (B+C)} ~,\\\ etiqueta {2.19}
\ frac {c-a} {c+a} ~&=~
\ frac {\ tan\;\ frac {1} {2} (C-A)} {\ tan\;\ frac {1} {2} (C+A)} ~. \\
\ fin {alinear}\]
Tenga en cuenta que ya que\(\tan\;(-\theta) = -\tan\;\theta \) para cualquier ángulo\(\theta \), podemos cambiar el orden de las letras en cada una de las fórmulas anteriores. Por ejemplo, podemos reescribir la ecuación\ ref {2.17} como
\ [\ label {2.20}
\ frac {b-a} {b+a} ~=~\ frac {\ tan\;\ frac {1} {2} (B-A)} {\ tan\;\ frac {1} {2} (B+A)} ~,
\]
y de manera similar para las demás fórmulas. Si\(a > b \), entonces suele ser más conveniente usar la Ecuación\ ref {2.17}, mientras que la Ecuación\ ref {2.20} es más conveniente cuando\(b > a \).
Resolver el triángulo\(\triangle\,ABC \) dado\(a =5 \)\(b = 3 \),, y\(C = 96^\circ \).
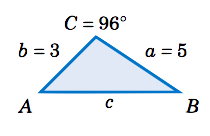
Solución
\(A + B + C = 180^\circ \), entonces\(A + B = 180^\circ - C = 180^\circ - 96^\circ = 84^\circ \). Así, por la Ley de las Tangentes,
\ [\ nonumber\ begin {align*}
\ frac {a-b} {a+b} ~=~\ frac {\ tan\;\ frac {1} {2} (A-B)} {\ tan\;\ frac {1} {2} (A+B)}\ quad&\ Rightarrow\ quad
\ frac {5-3} {5+3} ~=~\ frac {\ tan\;\ frac {1} {2} (A-B)} {\ tan\;\ frac {1} {2} (84^\ circ)}\\ nonumber
&\ Rightarrow\ quad\ tan\;\ tfrac {1} {2} (A- B) ~=~\ tfrac {2} {8}\ tan\; 42^\ circ ~=~ 0.2251\\ nonumber
&\ Rightarrow\ quad\ tfrac {1} {2} (A-B) ~=~ 12.7^\ circ\ quad\ Rightarrow\ quad A-B ~=~ 25.4^\ circ ~. \\
\ final {alinear*}\]
Ahora tenemos dos ecuaciones que involucran\(A \) y\(B \), que podemos resolver sumando las ecuaciones:
\ [\ nonumber\ begin {alignat*} {3}
A &- B &&=\; 25.4^\ circ\\\ nonumber
A &+ B &&=\; 84^\ circ\ phantom {4^\ circ}\\ [-2mm]\ nonumber
—&—&&—\ [-2mm]\ nonumber
2A\ phantom {+} &=\; 109.4^\ circ\ quad\ Rightarrow\ quad\ boxed {A = 54.7^\ circ}
\ quad\ Rightarrow\ quad B ~=~ 84^\ circ - 54.7^\ circ\ quad\ Rightarrow\ quad
\ quad\ boxed {B = 29.3^\ circ}\
\ end {alignat*}\ nonumber\]
Podemos encontrar el lado restante\(c \) usando la Ley de Sines:
\ [c ~=~\ frac {a\;\ sin\; C} {\ sin\; A} ~=~\ frac {5\;\ sin\; 96^\ circ} {\ sin\; 54.7^\ circ}
\ quad\ Rightarrow\ quad\ boxed {c = 6.09}\ nonumber\]
Tenga en cuenta que en cualquier triángulo\(\triangle\,ABC \), si\(a = b \) entonces\(A = B \) (¿por qué?) , y así ambos lados de la Ecuación\ ref {2.17} serían\(0 \) (since\(\tan\;0^\circ = 0\)). Esto quiere decir que la Ley de Tangentes no ayuda en el Caso 3 cuando los dos lados conocidos son iguales. Por esta razón, y quizás también por la forma algo inusual en la que se utiliza, la Ley de las Tangentes parece haber caído en desgracia en los libros de trigonometría últimamente. No parece tener ninguna ventaja sobre la Ley de Cosinos, que funciona incluso cuando los lados son iguales, requiere un poco menos pasos, y tal vez es más sencillo.
Relacionadas con la Ley de Tangentes están las ecuaciones de Mollweide:
Para cualquier triángulo\(\triangle\,ABC \),
\ [\ begin {align}
\ frac {a-b} {c} ~&=~
\ frac {\ sin\;\ frac {1} {2} (A-B)} {\ cos\;\ frac {1} {2} C} ~, ~\ texto {y}\ etiqueta {2.21}\\ [4pt]
\ frac {a+b} {c} ~&=~
frac {\ cos\;\ frac {1} {2} (A-B)} {\ sin\;\ frac {1} {2} C} ~. \ label {2.22}
\ end {align}\]
Tenga en cuenta que las seis partes de un triángulo aparecen en ambas ecuaciones de Mollweide. Por esta razón, cualquiera de las dos ecuaciones puede ser utilizada para verificar una solución de un triángulo. Si ambos lados de la ecuación coinciden (más o menos), entonces sabemos que la solución es correcta.
Utilice una de las ecuaciones de Mollweide para verificar la solución del triángulo del Ejemplo 2.10.
Solución
Recordemos que la solución completa fue\(a=5 \),\(b=3 \),\(c=6.09 \),\(A=54.7^\circ \),\(B=29.3^\circ \), y\(C=96^\circ \). Comprobaremos esto con la Ecuación\ ref {2.21}:
\ [\ begin {alinear*}
\ frac {a-b} {c} ~&=~\ frac {\ sin\;\ frac {1} {2} (A-B)} {\ cos\;\ frac {1} {2} C}\\\ nonumber
\ frac {5-3} {6.09} ~&=~
\ frac {\ sin\;\ frac {} {2} (54.7^\ circ - 29.3^\ circ)} {\ cos\;\ frac {1} {2} (96^\ circ)}\\\ nonumber
\ frac {2} {6.09} ~&=~\ frac {\ sin\ ; 12.7^\ circ} {\ cos\; 48^\ circ}\\ nonúmero
0.3284 ~&=~ 0.3285\ quad\ marca de verificación
\ final {alinear*}\]
La pequeña diferencia (\(\approx 0.0001\)) se debe a errores de redondeo de la solución original, por lo que podemos concluir que ambos lados de la ecuación coinciden, y de ahí que la solución sea correcta.
¿Puede un triángulo tener las partes\(a=6 \)\(b=7 \),\(c=9 \),\(A=55^\circ \),\(B=60^\circ \), y\(C=65^\circ\;\)?
Solución
Antes de usar las ecuaciones de Mollweide, las comprobaciones más simples son que los ángulos se suman\(180^\circ \) y que los lados más pequeños y más grandes son opuestos a los ángulos más pequeños y mayores, respectivamente. En este caso se mantienen todas esas condiciones. Así que consulta con la Ecuación de Mollweide\ ref {2.22}:
\ [\ nonumber\ begin {align*}
\ frac {a+b} {c} ~&=~\ frac {\ cos\;\ frac {1} {2} (A-B)} {\ sin\;\ frac {1} {2} C}\\\ nonumber
\ frac {6+7} {9} ~&=~
\ frac {\ cos\; frac {1} {2} (55^\ circ - 60^\ circ)} {\ sin\;\ frac {1} {2} (65^\ circ)}\\\ nonumber
\ frac {13} {9} ~&=~\ frac {\ cos \; (-2.5^\ circ)} {\ sin\; 32.5^\ circ}\\ nonúmero
1.44 ~&=~ 1.86\ quad\ veces
\ final {alinear*}\ nonumber\]
Aquí la diferencia es demasiado grande, por lo que concluimos que no hay triángulo con estas partes.
Demostraremos la Ley de Tangentes y las ecuaciones de Mollweide en el Capítulo 3, donde podremos suministrar breves pruebas analíticas.


