2.4: El Área de un Triángulo
- Page ID
- 113479
En geometría elemental aprendiste que el área de un triángulo es la mitad de la base por la altura. Ahora usaremos eso, combinado con alguna trigonometría, para derivar más fórmulas para el área cuando se le den varias partes del triángulo.
Caso 1: Dos lados y el ángulo incluido.
Supongamos que tenemos un triángulo\(\triangle\,ABC \), en el que\(A \) puede ser agudo, un ángulo recto, u obtuso, como en la Figura 2.4.1. Supongamos que\(A \)\(b \),, y\(c \) son conocidos.
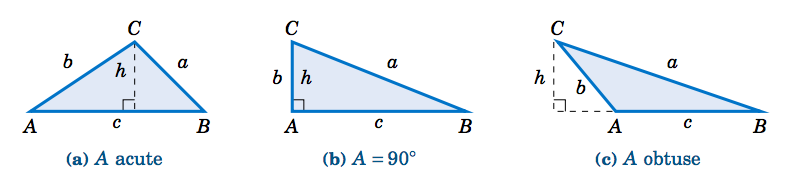
En cada caso dibujamos una altitud de altura\(h \) desde el vértice\(C \) a\(\overline{AB} \), de manera que el área (que denotaremos por la letra\(K\)) viene dada por\(K = \frac{1}{2}hc \). Pero vemos eso\(h = b\;\sin\;A \) en cada uno de los triángulos (ya\(\;h=b \) y\(\sin\;A = \sin\;90^\circ = 1 \) en la Figura 2.4.1 (b), y\(\;h = b\;\sin\;(180^\circ - A) =b\;\sin\;A \) en la Figura 2.4.1 (c)). Así obtenemos la siguiente fórmula:
\[\fbox{\(\text{Area} ~=~ K ~=~ \tfrac{1}{2}\,bc\;\sin\;A\)}\label{2.23} \]
La fórmula anterior para el área de\(\triangle\,ABC \) es en términos de las partes conocidas\(A \),\(b \), y\(c \). Argumentos similares para los ángulos\(B \) y nos\(C \) dan:
\ [\ begin {align}\ text {Área} ~&=~ K =~\ tfrac {1} {2}\, ac\;\ sin\; B\\
\ texto {Área} ~&=~ K =~\ tfrac {1} {2}\, ab\;\ sin\; C\ etiqueta {2.25}\ end {align}\]
Observe que la altura\(h \) no aparece explícitamente en estas fórmulas, aunque está implícitamente ahí. Estas fórmulas tienen la ventaja de estar en cuanto a partes del triángulo, sin tener que encontrar\(h \) por separado.
Encuentra el área del triángulo\(\triangle\,ABC \) dado\(A = 33^\circ \),\(b = 5 \), y\(c = 7 \).
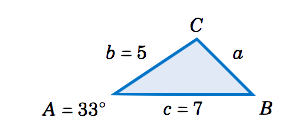
Solución
Usando la ecuación\ ref {2.23}, el área\(K \) viene dada por:
\ [\ nonumber\ begin {align*}
K ~&=~\ tfrac {1} {2}\, bc\;\ sin\; A\\ nonúmero
&=~\ tfrac {1} {2}\, (5) (7)\;\ sin\; 33^\ circ\\ número
K ~&=~ 9.53
\ end {align*}\]
Caso 2: Tres ángulos y cualquier lado.
Supongamos que tenemos un triángulo\(\triangle\,ABC \) en el que se conocen un lado\(a \), digamos,, y los tres ángulos. Por la Ley de Sines sabemos que
\ [\ nonúmero
c ~=~\ frac {a\;\ sin\; C} {\ sin\; A} ~,
\ etiqueta {2.24}\]
así que sustituyendo esto en la Ecuación\ ref {2.24} obtenemos:
\ [\ fbox {\ (\ text {Área} ~=~ K ~=~\ frac {a^2\;\ sin\; B\;\ sin\; C} {2\;\ sin\; A}
\)}\ label {2.26}\] Argumentos
similares para los lados\(b \) y nos\(c \) dan:
\ [\ begin {align}
\ text {Área} ~&=~ K =~\ frac {b^2\;\ sin\; A\;\ sin\; C} {2\;\ sin\; B}\ etiqueta {2.27}\\
\ texto {Área} ~&=~ K =~\ frac {c^2\;\ sin\; A\;\ sin\; B} {2\;\ sin\; C}\ etiqueta {2.28}
\ end {align}\ nonumber\]
Encuentra el área del triángulo\(\triangle\,ABC \) dado\\(A = 115^\circ \)\(B=25^\circ \),\(C=40^\circ \), y\(a = 12 \).
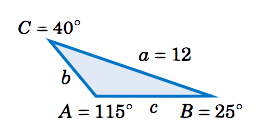
Solución
Usando la ecuación\ ref {2.26}, el área\(K \) viene dada por:
\ [\ begin {align*}
K ~&=~\ frac {a^2\;\ sin\; B\;\ sin\; C} {2\;\ sin\; A}\\
&=~\ frac {12^2\;\ sin\; 25^\ circ\;\ sin\; 40^\ circ} {2\;\ sin\; 115^\ circ}\\
K ~&=~ 21.58
\ final {alinear*} \]
Caso 3: Tres lados.
Supongamos que tenemos un triángulo\(\triangle\,ABC \) en el que se conocen los tres lados. Entonces la fórmula de Heron nos da el área:
Para un triángulo\(\triangle\,ABC \) con lados\(a \),\(b \), y\(c \), let\(s = \frac{1}{2}\,(a+b+c) \) (es decir,\(2s = a+b+c \) es el perímetro del triángulo). Entonces el área\(K \) del triángulo es
\[ \text{Area} ~=~ K ~=~ \sqrt{s\,(s-a)\,(s-b)\,(s-c)} ~~.\label{2.29} \]
Para probar esto, primero recuerda que el área\(K \) es la mitad de la base por la altura. Usando\(c \) como base y la altitud\(h \) como altura, como antes en la Figura 2.4.1, tenemos\(K = \frac{1}{2}hc \). Al cuadrar ambos lados nos da
\ [
K^2 =\ tfrac {1} {4}\, h^2 c^2 ~.
\ label {2.30}\]
En la Figura 2.4.2, deja\(D \) ser el punto donde toca la altitud\(\overline{AB} \) (o su extensión).
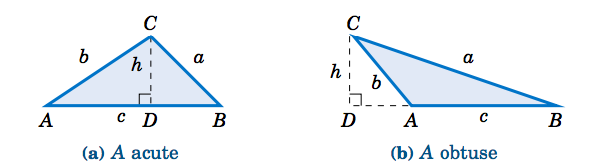
Por el Teorema de Pitágoras, vemos eso\(\;h^2 = b^2 - (AD)^2 \). En la Figura 2.4.2 (a), vemos eso\(\;AD = b\;\cos\;A \). Y en la Figura 2.4.2 (b) vemos eso\(\;AD = b\;\cos (180^\circ - A) = -b\cos\;A \). De ahí, en cualquier caso tenemos\(\;(AD)^2 = b^2 \;(\cos\;A)^2 \), y así
\[h^2 ~=~ b^2 - b^2 \;(\cos\;A)^2 ~=~ b^2 \,(1 - (\cos\;A)^2 ) ~=~ b^2 \,(1+ \cos\;A)\,(1- \cos\;A)~.\label{2.31} \]
(Tenga en cuenta que la ecuación anterior también se mantiene cuando\(A=90^\circ \) since\(\cos\;90^\circ =0 \) y\(h=b\)). Así, sustituyendo la Ecuación\ ref {2.31} en la Ecuación\ ref {2.30}, tenemos
\ [
K^2 =\ tfrac {1} {4}\, b^2 c^2\, (1+\ cos\; A)\, (1-\ cos\; A) ~.
\ label {2.32}\]
Por la Ley de Cosines sabemos que
\ [\ nonumber\ begin {align*}
1 +\ cos\; A ~&=~ 1 +\ frac {b^2 + c^2 - a^2} {2bc} ~=~\ frac {2bc + b^2 + c^2 - a^2} {2bc}
~=~\ frac {(b+c) ^2 - a^2} {2bc} ~=~\ frac {((b+c) + a)\, ((b+c) - a)} {2bc}\\\ nonumber
&=~\ frac {(a + b + c)\, (b + c - a)} {2bc} ~,
\ end { alinear*}\]
y de manera similar
\ [\ nonumber\ begin {align*}
1 -\ cos\; A ~&=~ 1 -\ frac {b^2 + c^2 - a^2} {2bc} ~=~\ frac {2bc - b^2 - c^2 + a^2} {2bc}
~=~\ frac {a^2 - (b-c) ^2} {2bc} =~\ frac {(a - (b-c))\, (a + (b-c))} {2bc}\\\ nonumber
&=~\ frac {(a - b + c)\, (a + b - c)} {2bc} ~.
\ end {alinear*}\]
Así, sustituyendo estas expresiones en la Ecuación\ ref {2.32}, tenemos
\ [\ nonumber\ begin {align}
K^2 ~&=~\ tfrac {1} {4}\, b^2 c^2\;\ frac {(a + b + c)\, (b + c - a)} {2bc}\;\ cdot\;
\ frac {(a - b + c)\, (a + b - c)} {2bc}\\\ nonúmero
&=~\ frac {a + b + c} {2}\;\ cdot\;\ frac {b + c - a} {2}\;\ cdot\;\ frac {a - b + c} {2}\;\ cdot\;
\ frac {a + b - c} {2} ~,\\\ end {align}\ nonumber\]
y como definimos\(s = \frac{1}{2}\,(a+b+c) \), vemos que
\[\nonumber K^2 ~=~ s\,(s-a)\,(s-b)\,(s-c) ~, \nonumber \]
así al tomar raíces cuadradas obtenemos
\[\nonumber K ~=~ \sqrt{s\,(s-a)\,(s-b)\,(s-c)} ~~.\quad \textbf{QED} \nonumber \]
Encuentra el área del triángulo\(\triangle\,ABC \) dado\(a=5 \),\(b=4 \), y\(c = 7 \).
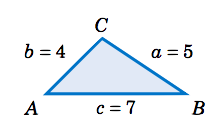
Solución
Usando la fórmula de Heron con\(s = \frac{1}{2}\,(a+b+c) = \frac{1}{2}\,(5+4+7) = 8 \), el área\(K \) viene dada por:
\ [\ begin {align*}
K ~&=~\ sqrt {s\, (s-a)\, (s-b)\, (s-c)}\\
&=~\ sqrt {8\, (8-5)\, (8-4)\, (8-7)} ~=~\ sqrt {96}\ quad\ Rightarrow\ quad\ en caja {K ~=~ 4\,\ sqrt {6}
~\ aprox~ 9.8} ~.
\ end {alinear*}\]
La fórmula de Heron es útil para fines teóricos (por ejemplo, para derivar otras fórmulas). Sin embargo, no es muy adecuado para el uso de la calculadora, exhibiendo lo que se denomina inestabilidad numérica para triángulos “extremos”, como en el siguiente ejemplo.
Encuentra el área del triángulo\(\triangle\,ABC \) dado\(a=1000000 \),\(b=999999.9999979 \), y\(c = 0.0000029 \).
Solución:
Para usar la fórmula de Heron, necesitamos calcular\(s = \frac{1}{2}\,(a+b+c) \). Observe que el valor real de\(a+b+c \) es\(2000000.0000008 \), que tiene\(14 \) dígitos. La mayoría de las calculadoras pueden almacenar\(12\) -\(14 \) dígitos internamente (incluso si muestran menos), y por lo tanto pueden redondear ese valor de\(a+b+c \) a\(2000000 \). Cuando luego dividimos ese valor redondeado para\(a+b+c \) por\(2 \) para obtener\(s \), algunas calculadoras (por ejemplo, el TI-83 Plus) darán un valor redondeado a la baja de\(1000000 \).
Esto es un problema porque\(a=1000000 \), y así lo conseguiríamos\(s-a=0 \), haciendo que la fórmula de Heron nos diera un área de ¡\(0 \)para el triángulo! Y esta es efectivamente la respuesta incorrecta que devuelve el TI-83 Plus. Otras calculadoras pueden dar alguna otra respuesta inexacta, dependiendo de cómo almacenen los valores internamente. El área real -precisa a los\(15\) decimales- es\(K = 0.99999999999895 \), es decir, lo es básicamente\(1 \).
El ejemplo anterior muestra lo problemática que puede ser la aritmética de coma flotante. Por suerte hay una mejor fórmula para el área de un triángulo cuando se conocen los tres lados:
Para un triángulo\(\triangle\,ABC \) con lados\(a \ge b \ge c \), el área es:
\[ \text{Area} ~=~ K ~=~ \tfrac{1}{4}\,\sqrt{(a + (b+c))\,(c - (a-b))\,(c + (a-b))\,(a + (b-c))}\label{2.33} \]
Para usar esta fórmula, ordene los nombres de los lados para que\(a \ge b \ge c \). Después realizar las operaciones dentro de la raíz cuadrada en el orden exacto en que aparecen en la fórmula, incluyendo el uso de paréntesis. Después toma la raíz cuadrada y divídala por\(4 \). Para el triángulo en el Ejemplo 2.16, la fórmula anterior da una respuesta de exactamente\(K = 1 \) en la misma calculadora TI-83 Plus que falló con la fórmula de Heron. ¡Lo asombroso de esta fórmula es que es solo la fórmula de Heron reescrita! El uso de paréntesis es lo que obliga al orden correcto de las operaciones para la estabilidad numérica.
Otra fórmula para el área de un triángulo dados sus tres lados se da a continuación:
Para un triángulo\(\triangle\,ABC \) con lados\(a \ge b \ge c \), el área es:
\[\label{2.34} \text{Area} ~=~ K ~=~ \tfrac{1}{2}\,\sqrt{a^2 c^2 ~-~ \left( \tfrac{a^2 + c^2 - b^2}{2} \right)^2} \]


