2.5: Círculos circunscritos e inscritos
- Page ID
- 113491
Recordemos de la Ley de los Sinos que cualquier triángulo\(\triangle\,ABC\) tiene una proporción común de lados a senos de ángulos opuestos, a saber
\ [\ frac {a} {\ sin\; A} ~=~\ frac {b} {\ sin\; B} ~=~\ frac {c} {\ sin\; C} ~.
\ nonumber\]
Esta relación común tiene un significado geométrico: es el diámetro (es decir, el doble del radio) del círculo único en el que se\(\triangle\,ABC\) puede inscribir, llamado círculo circunscrito del triángulo. Antes de probarlo, necesitamos revisar algunas geometrías elementales.
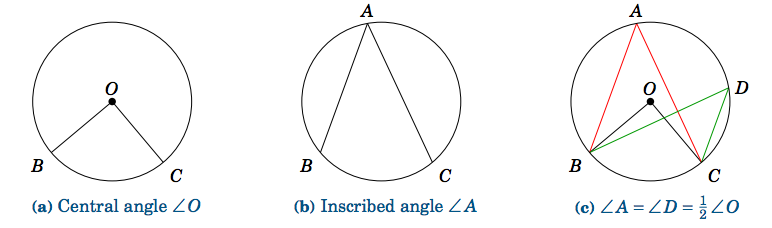
Un ángulo inscrito de un círculo es un ángulo cuyo vértice es un punto\(A\) en el círculo y cuyos lados son segmentos de línea (llamados acordes) desde\(A\) otros dos puntos del círculo. En la Figura 2.5.1 (b),\(\angle\,A\) se encuentra un ángulo inscrito que intercepta el arco\(\overparen{BC} \). Aquí declaramos sin pruebas una relación útil entre ángulos inscritos y centrales:
Si un ángulo inscrito\(\angle\,A\) y un ángulo central\(\angle\,O\) interceptan el mismo arco, entonces\(\angle\,A = \frac{1}{2}\,\angle\,O\, \). Así, los ángulos inscritos que interceptan el mismo arco son iguales.
La figura 2.5.1 (c) muestra dos ángulos inscritos,\(\angle\,A\) y\(\angle\,D \), que interceptan el mismo arco\(\overparen{BC}\) que el ángulo central\(\angle\,O \), y por lo tanto\(\angle\,A = \angle\,D = \frac{1}{2}\,\angle\,O\) (así\(\;\angle\,O = 2\,\angle\,A = 2\,\angle\,D\,) \).
Ahora probaremos nuestra afirmación sobre la proporción común en la Ley de los Sines:
Para cualquier triángulo\(\triangle\,ABC \), el radio\(R\) de su círculo circunscrito viene dado por:
\[2\,R ~=~ \frac{a}{\sin\;A} ~=~ \frac{b}{\sin\;B} ~=~ \frac{c}{\sin\;C}\label{2.35} \]
Nota: Para un círculo de diámetro\(1 \), esto significa\(a=\sin\;A \),\(b=\sin\;B \), y\(c=\sin\;C \).)
Para probarlo, dejemos\(O\) ser el centro del círculo circunscrito para un triángulo\(\triangle\,ABC \). Entonces\(O\) puede ser ya sea dentro, fuera, o en el triángulo, como en la Figura 2.5.2 a continuación. En los dos primeros casos, dibuje un segmento de línea perpendicular de\(O\) a\(\overline{AB}\) en el punto\(D \).
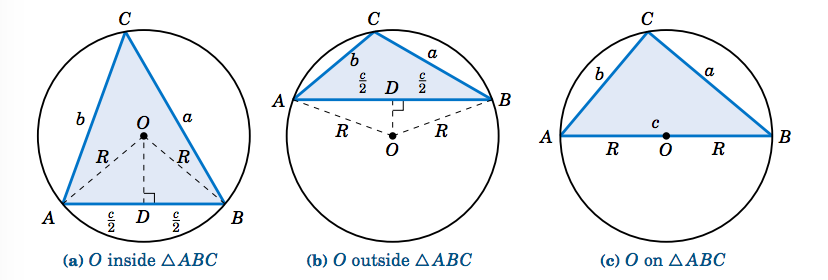
Los radios\(\overline{OA}\) y\(\overline{OB}\) tienen la misma longitud\(R \), por lo que\(\triangle\,AOB\) es un triángulo isósceles. Así, a partir de la geometría elemental sabemos que\(\overline{OD}\) biseca tanto el ángulo\(\angle\,AOB\) como el lateral\(\overline{AB} \). Entonces\(\angle\,AOD = \frac{1}{2}\,\angle\,AOB\) y\(AD = \frac{c}{2} \). Pero como el ángulo inscrito\(\angle\,ACB\) y el ángulo central\(\angle\,AOB\) interceptan el mismo arco\(\overparen{AB} \), sabemos por el Teorema 2.4 que\(\angle\,ACB = \frac{1}{2}\,\angle\,AOB \). De ahí,\(\angle\,ACB = \angle\,AOD \). Así que desde\(C =\angle\,ACB \), tenemos
\ [\ sin\; C ~=~\ sin\;\ ángulo\, AOD ~=~\ frac {AD} {OA} ~=~\ frac {\ frac {c} {2}} {R} ~=~\ frac {c} {2R}
\ quad\ Rightarrow\ quad 2\, R ~=~\ frac {c} {\ sin\; C},
\ nonumber\]
por lo que por la Ley de Sines el resultado sigue si\(O\) está dentro o fuera\(\triangle\,ABC \).
Ahora supongamos que\(O\) está encendido\(\triangle\,ABC \), digamos, en el lado\(\overline{AB} \), como en la Figura 2.5.2 (c). Entonces\(\overline{AB}\) es un diámetro del círculo, así\(C = 90^\circ\) por el Teorema de Thales. De ahí\(\sin\;C = 1 \),, y así\(2\,R = AB = c = \frac{c}{1} = \frac{c}{\sin\;C}\; \), y el resultado vuelve a seguir por la Ley de los Sines. QED
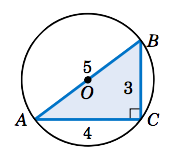
Solución:
Sabemos que\(\triangle\,ABC\) es un triángulo rectángulo. Entonces, como vemos en la Figura 2.5.3,\(\sin\;A = 3/5 \). Por lo tanto,
\[ 2\,R ~=~ \frac{a}{\sin\;A} ~=~ \frac{3}{\frac{3}{5}} ~=~ 5 \quad\Rightarrow\quad \boxed{R ~=~ 2.5} ~.\nonumber \]
Tenga en cuenta que ya que\(R =2.5 \), el diámetro del círculo es\(5 \), que es el mismo que\(AB \). Así,\(\overline{AB}\) debe ser un diámetro del círculo, y así el centro\(O\) del círculo es el punto medio de\(\overline{AB} \).
Para cualquier triángulo rectángulo, la hipotenusa es un diámetro del círculo circunscrito, es decir, el centro del círculo es el punto medio de la hipotenusa.
Para el triángulo rectángulo en el ejemplo anterior, el círculo circunscrito es simple de dibujar; su centro se puede encontrar midiendo una distancia de\(2.5\) unidades\(A\) a lo largo\(\overline{AB} \).
Necesitamos un procedimiento diferente para los triángulos agudos y obtusos, ya que para un triángulo agudo el centro del círculo circunscrito estará dentro del triángulo, y estará afuera para un triángulo obtuso. Observe de la prueba del Teorema 2.5 que el centro\(O\) estaba en la bisectriz perpendicular de uno de los lados (\(\overline{AB}\)). Argumentos similares para los otros lados mostrarían que\(O\) está en los bisectores perpendiculares para esos lados:
Para cualquier triángulo, el centro de su círculo circunscrito es la intersección de los bisectores perpendiculares de los lados.
Encuentra el radio\(R\) del círculo circunscrito para el triángulo\(\triangle\,ABC\) del Ejemplo 2.6 en la Sección 2.2:\(a = 2 \),\(b = 3 \), y\(c = 4 \). Después dibuja el triángulo y el círculo.
Solución:
En el Ejemplo 2.6 encontramos\(A=28.9^\circ \), así\(2\,R = \frac{a}{\sin\;A} = \frac{2}{\sin\;28.9^\circ} = 4.14 \), así\(\boxed{R = 2.07}\; \).
En la Figura 2.5.5 (a) mostramos cómo dibujar\(\triangle\,ABC\): usar una regla para dibujar el lado más largo\(\overline{AB}\) de la longitud\(c=4 \), luego usar una brújula para dibujar arcos de radio\(3\) y\(2\) centrados en\(A\) y\(B \), respectivamente. La intersección de los arcos es el vértice\(C \).
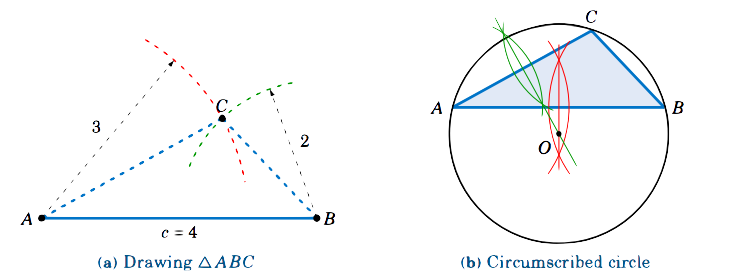
En la Figura 2.5.5 (b) mostramos cómo dibujar el círculo circunscrito: dibujar los bisectores perpendiculares de\(\overline{AB}\) y\(\overline{AC}\); su intersección es el centro\(O\) del círculo. Usa una brújula para dibujar el círculo centrado en\(O\) el que pasa\(A \).
El teorema 2.5 se puede utilizar para derivar otra fórmula para el área de un triángulo:
Para un triángulo\(\triangle\,ABC \), deja\(K\) ser su área y dejar\(R\) ser el radio de su círculo circunscrito. Entonces
\[K ~=~ \frac{abc}{4\,R} \quad ( \text{and hence }\; R ~=~ \frac{abc}{4\,K} ~) ~. \label{2.36} \]
Para probar esto, tenga en cuenta que por Teorema 2.5 tenemos
\ [2\, R ~=~\ frac {a} {\ sin\; A} ~=~\ frac {b} {\ sin\; B} ~=~\ frac {c} {\ sin\; C}\ quad\ Rightarrow\ quad
\ sin\; A ~=~\ frac {a} {2\, R} ~, ~~\ sin\; B ~=~\ frac {b} {2\, R} ~, ~~\ sin\; C ~=~\ frac {c} {2\, R} ~.
\ nonumber\]
Sustituya esas expresiones en la Ecuación 2.26 de la Sección 2.4 para el área\(K\):
\ [K ~=~\ frac {a^2\;\ sin\; B\;\ sin\; C} {2\;\ sin\; A} ~=~
\ frac {a^2\;\ cdot\;\ frac {b} {2\, R}\;\ cdot\;\ frac {c} {2\, R}} {2\;\ cdot\;\ frac {a} {2\, R}}
~=~\ frac {abc} {4\, R}\ qquad\ textbf {QED}
\ nonumber\]
Combinando el Teorema 2.8 con la fórmula de Heron para el área de un triángulo, obtenemos:
Para un triángulo\(\triangle\,ABC \), vamos\(s = \frac{1}{2}(a+b+c) \). Entonces el radio\(R\) de su círculo circunscrito es
\[R ~=~ \frac{abc}{4\,\sqrt{s\,(s-a)\,(s-b)\,(s-c)}} ~~.\label{2.37} \]
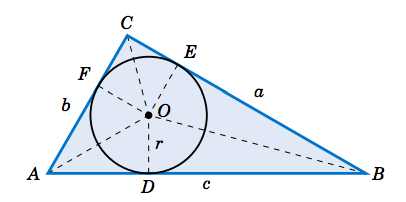
Dejar\(r\) ser el radio del círculo inscrito, y dejar,\(D \)\(E \), y\(F\) ser los puntos en\(\overline{AB} \),, y\(\overline{BC} \), respectivamente\(\overline{AC} \), en los que el círculo es tangente. Entonces\(\overline{OD} \perp \overline{AB} \),\(\overline{OE} \perp \overline{BC} \), y\(\overline{OF} \perp \overline{AC} \). Así,\(\triangle\,OAD\) y\(\triangle\,OAF\) son triángulos equivalentes, ya que son triángulos rectos con la misma hipotenusa\(\overline{OA}\) y con patas correspondientes\(\overline{OD}\) y\(\overline{OF}\) de la misma longitud\(r \). De ahí\(\angle\,OAD =\angle\,OAF \),, lo que significa que\(\overline{OA}\) biseca el ángulo\(A \). De igual manera,\(\overline{OB}\) bisectos\(B\) y\(\overline{OC}\) bisectos\(C \). Por lo tanto, hemos demostrado:
Para cualquier triángulo, el centro de su círculo inscrito es la intersección de los bisectores de los ángulos.
Utilizaremos la Figura 2.5.6 para encontrar el radio\(r\) del círculo inscrito. Desde los\(\overline{OA}\) bisectos\(A \), vemos eso\(\tan\;\frac{1}{2}A = \frac{r}{AD} \), y así\(r = AD \,\cdot\, \tan\;\frac{1}{2}A \). Ahora,\(\triangle\,OAD\) y\(\triangle\,OAF\) son triángulos equivalentes, entonces\(AD =AF \). De igual manera,\(DB = EB\) y\(FC = CE \). Así, si lo dejamos\(s=\frac{1}{2}(a+b+c) \), vemos que
\ [\ nonumber\ begin {align*}
2\, s ~&=~ a ~+~ b ~+~ c ~=~ (AD + DB) ~+~ (CE + EB) ~+~ (AF + FC)\\ nonúmero
&=~ AD ~+~ EB ~+~ CE ~+~ CE ~+~ EB ~+~ AD ~+~ CE ~+~ CE ~=~ 2\, (AD + EB + CE)\\\ nonumber
s ~&=~ AD ~+~ EB ~+~ CE ~=~ AD ~+~ a\\ no numerado
AD ~&=~ s - a ~.
\ end {align*}\ nonumber\]
De ahí,\(r = (s-a)\,\tan\;\frac{1}{2}A \). Argumentos similares para los ángulos\(B\) y nos\(C\) dan:
Para cualquier triángulo\(\triangle\,ABC \), vamos\(s = \frac{1}{2}(a+b+c) \). Entonces el radio\(r\) de su círculo inscrito es
\ [r ~=~ (s-a)\,\ tan\;\ tfrac {1} {2} A ~=~ (s-b)\,\ tan\;\ tfrac {1} {2} B ~=~
(s-c)\,\ tan\;\ tfrac {1} {2} C ~. \ label {2.38}\]
También vemos en la Figura 2.5.6 que el área del triángulo\(\triangle\,AOB\) es
\ [\ texto {Área} (\ triángulo\, AOB) ~=~\ tfrac {1} {2}\,\ texto {base}\ veces\ texto {altura} ~=~
\ tfrac {1} {2}\, c\, r ~.
\ nonumber\]
De igual manera,\(\text{Area}(\triangle\,BOC) = \frac{1}{2}\,a\,r\) y\(\text{Area}(\triangle\,AOC) = \frac{1}{2}\,b\,r \). Así, el área\(K\) de\(\triangle\,ABC\) es
\ [\ nonumber\ begin {align*}
K ~&=~\ texto {Área} (\ triángulo\, AOB) ~+~\ texto {Área} (\ triángulo\, BOC) ~+~\ texto {Área} (\ triángulo\, AOC)
~=~\ tfrac {1} {2}\, c\, r ~+~\ tfrac {1} {2}\, a\, r ~+~\ tfrac {1} {2}\, b\, r\\ nonumber
&=~\ tfrac {1} {2}\, (a+b+c)\, r ~=~ sr ~, ~\ text {así por La fórmula de Heron obtenemos}\\\ nonumber
r ~&=~\ frac {K} {s} ~=~\ frac {\ sqrt {s\, (s-a)\, (s-b)\, (s-c)}} {s} ~=~
\ sqrt {\ frac {s\, (s-a)\, (s-b)\, (s-c)} s^2}} ~=~\ sqrt {\ frac {(s-a)\, (s-b)\, (s-c)} {s}} ~~.
\ end {align*}\ nonumber\]
Así, hemos demostrado el siguiente teorema:
Para cualquier triángulo\(\triangle\,ABC \), vamos\(s = \frac{1}{2}(a+b+c) \). Entonces el radio\(r\) de su círculo inscrito es
\[\label{2.39}r ~=~ \frac{K}{s} ~=~ \sqrt{\frac{(s-a)\,(s-b)\,(s-c)}{s}} ~~. \]
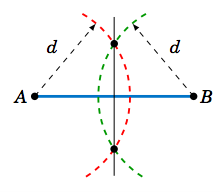
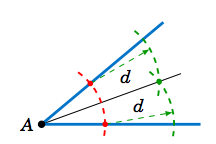
Recordemos de la geometría cómo bisectar un ángulo: use una brújula centrada en el vértice para dibujar un arco que intersecta los lados del ángulo en dos puntos. En esos dos puntos usa una brújula para dibujar un arco con el mismo radio, lo suficientemente grande como para que los dos arcos se crucen en un punto, como en la Figura 2.5.7. La línea que atraviesa ese punto y el vértice es la bisectriz del ángulo. Para el círculo inscrito de un triángulo, solo se necesitan dos bisectores angulares; su intersección será el centro del círculo.
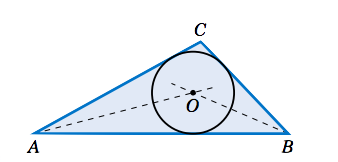
Encuentra el radio\(r\) del círculo inscrito para el triángulo\(\triangle\,ABC\) del Ejemplo 2.6 en la Sección 2.2:\(a = 2 \),\(b = 3 \), y\(c = 4 \). Dibuja el círculo.
Solución:
Usando el Teorema 2.11 con\(s = \frac{1}{2}(a+b+c) =\frac{1}{2}(2+3+4) = \frac{9}{2} \), tenemos
\ [r ~=~\ sqrt {\ frac {(s-a)\, (s-b)\, (s-c)} {s}} ~=~
\ sqrt {\ frac {\ frac {\ izquierda (\ frac {9} {2} {2} {2} -
4\ derecha)} {\ frac {9} {2}}} ~=~\ sqrt {\ frac {5} {12}} ~. \ nonumber\]
La Figura 2.5.8 muestra cómo dibujar el círculo inscrito: dibujar los bisectores de\(A\) y\(B \), luego en su intersección, usar una brújula para dibujar un círculo de radio\(r = \sqrt{5/12} \approx 0.645 \).


