2.E: Triángulos generales (Ejercicios)

Estos son ejercicios de tarea para acompañar el mapa de texto “Trigonometría Primaria” de Corral. Se trata de un texto sobre trigonometría elemental, diseñado para estudiantes que han cursado cursos de álgebra y geometría de secundaria. Aunque está diseñado para estudiantes universitarios, también podría usarse en escuelas secundarias. Se cubren los temas tradicionales, pero se toma un enfoque más geométrico de lo habitual. También se discuten algunos métodos numéricos (por ejemplo, el método secante para resolver ecuaciones trigonométricas).

2.1 Ejercicios

Para los Ejercicios 1-9, resuelve el triángulo\(△ ABC\).

2.1.1\(a = 10, A = 35^\circ , B = 25^\circ \)

2.1.2\(b = 40, B = 75^\circ , c = 35 \)

2.1.3\(A = 40^\circ , B = 45^\circ , c = 15 \)

2.1.4\(a = 5, A = 42^\circ , b = 7 \)

2.1.5\(a = 40, A = 25^\circ , c = 30 \)

2.1.6\(a = 5, A = 47^\circ , b = 9 \)

2.1.7\(a = 12, A = 94^\circ , b = 15 \)

2.1.8\(a = 15, A = 94^\circ , b = 12 \)

2.1.9\(a = 22, A = 50^\circ , c = 27\)

2.1.10 Dibuja un círculo con un radio de 2 pulgadas e inscribe un triángulo dentro del círculo. Usa una regla y un prolongador para medir los lados\(a, b, c\) y los ángulos\(A, B, C\) del triángulo. La Ley de Sines dice que los ratios\(\frac{a}{ \sin A} , \frac{b}{ \sin B} , \frac{c}{ \sin C}\) son iguales. Verifica esto para tu triángulo. ¿Qué relación tiene esa relación común con el diámetro de tu círculo?

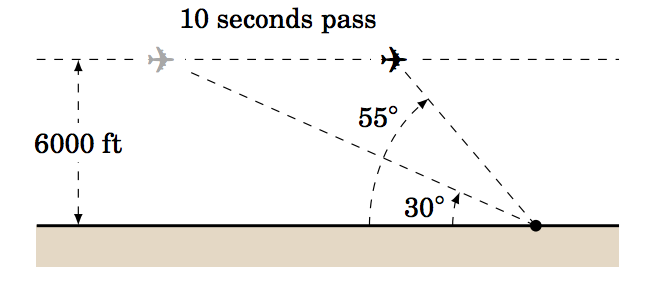
2.1.11 Un observador en el suelo mide un ángulo de inclinación de\(30^\circ\) a un avión que se aproxima, y 10 segundos después mide un ángulo de inclinación de\(55^\circ\). Si el avión está volando a una velocidad constante y a una altitud constante de 6000 pies en línea recta directamente sobre el observador, encuentre la velocidad del avión en millas por hora. (Nota: 1 milla = 5280 ft)

2.1.12 Probar la Ley de los Senos para los triángulos rectos. (Pista: Se conoce uno de los ángulos. )

2.1.13 Para un triángulo\(△ ABC\), muéstralo\(\frac{a± b}{ c} = \frac{\sin A ± \sin B}{ \sin C}\).

2.1.14 Para un triángulo\(△ ABC\), muéstralo\(\frac{a}{ c} = \frac{\sin (B +C)}{ \sin C}\).

2.1.15 Una diagonal de un paralelogramo mide 17 cm de largo y hace ángulos de\(36^\circ\) y\(15^\circ\) con los lados. Encuentra los largos de los lados.

2.1.16 Explique por qué en el Caso 1 (un lado y dos ángulos) siempre hay exactamente una solución.

---

2.2 Ejercicios

Para los Ejercicios 1-6, resuelve el triángulo\(\triangle\,ABC \).

2.2.1\(A = 60^\circ \),\(b = 8 \),\(c = 12\)

2.2.2\(A = 30^\circ \),\(b = 4 \),\(c = 6\)

2.2.3\(a = 7 \),\(B = 60^\circ \),\(c = 9\)

2.2.4\(a = 7 \),\(b = 3 \),\(c = 9\)

2.2.5\(a = 6 \),\(b = 4 \),\(c = 1\)

2.2.6\(a = 11 \),\(b = 13 \),\(c = 16\)

2.2.7 El diagonales de un paralelogramo se cruzan en\(42^\circ \) ángulo y tienen longitudes de\(12 \) y\(7 \) cm. Encuentra las longitudes de los lados del paralelogramo. (Pista: Las diagonales se bisecan entre sí.)

2.2.8 Dos trenes salen de la misma estación al mismo tiempo, moviéndose por vías rectas que forman un\(35^\circ \) ángulo. Si un tren viaja a una velocidad promedio de\(100 \) mi/hr y el otro a una velocidad promedio de\(90 \) mi/hr, ¿a qué distancia están los trenes después de media hora?

2.2.9 Tres círculos con radios de\(4 \)\(5 \), y\(6 \) cm, respectivamente, son tangentes entre sí externamente. Encuentra los ángulos del triángulo cuyos vértice son los centros de los círculos.

2.2.10 Encuentra la longitud\(x \) de la diagonal del cuadrilátero en la Figura 2.2.3 a continuación.

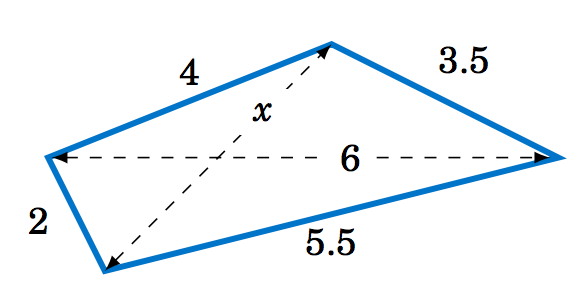
Figura 2.2.3 Ejercicio 10

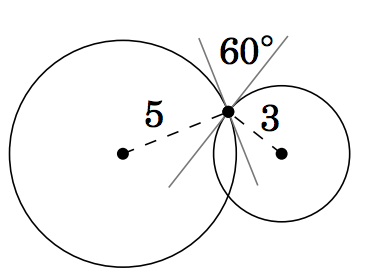
Figura 2.2.4 Ejercicio 11

2.2.11 Dos círculos de radios\(5 \) y\(3 \) cm, respectivamente, se cruzan en dos puntos. En cualquier punto de intersección, las líneas tangentes a los círculos forman un\(60^\circ\) ángulo, como en la Figura 2.2.4 anterior. Encuentra la distancia entre los centros de los círculos.

2.2.12 Usa la Ley de Cosinos para mostrar eso para cualquier triángulo\(\triangle\,ABC \),\(c^2 < a^2 + b^2 \) si\(C \) es agudo,\(c^2 > a^2 + b^2 \) si\(C \) es obtuso, y\(c^2 = a^2 + b^2\) si\(C \) es un ángulo recto.

2.2.13 Mostrar que para cualquier triángulo\(\triangle\,ABC \),
\ [\ nonumber
\ frac {\ cos\; A} {a} ~+~\ frac {\ cos\; B} {b} ~+~\ frac {\ cos\; C} {c} ~=~\ frac {a^2 + b^2 + c^2} {2abc} ~.
\]

2.2.14 Mostrar que para cualquier triángulo\(\triangle\,ABC \),
\ [\ nonumber
\ cos\; A ~+~\ cos\; B ~+~\ cos\; C ~=~\ frac {a^2\ ;( b+c-a) ~+~ b^2\ ;( a+c-b) ~+~ c^2\ ;( a+b-c)} {2abc} ~.
\]
¿Qué representan geométricamente los términos entre paréntesis? Usa tu respuesta para explicar por qué\(\;\cos\;A ~+~ \cos\;B ~+~ \cos\;C ~>~0\, \) para cualquier triángulo, aunque uno de los cosenos sea negativo.

2.2.15 Probar la Ley de los Cosinos (es decir, Ecuaciones 2.9-2.11) para triángulos rectos.

2.2.16 Recordemos de la geometría elemental que una mediana de un triángulo es un segmento de línea desde cualquier vértice hasta el punto medio del lado opuesto. Mostrar que la suma de los cuadrados de las tres medianas de un triángulo es\(\frac{3}{4}\) la suma de los cuadrados de los lados.

2.2.17 El astrónomo y matemático holandés Willebrord Snell (1580-1626) escribió la Ley de Cosines como
\ [
\ frac {2ab} {c^2\; -\; (a - b) ^2} ~=~\ frac {1} {1\; -\;\ cos\; C}
\]
en su texto de trigonometría Doctrina triangulorum (publicada un año después de su muerte). Demostrar que esta fórmula es equivalente a la Ecuación 2.11 en nuestro enunciado de la Ley de Cosinos.

2.2.18 Supongamos que un satélite en el espacio, una estación terrestre y el centro de la tierra se encuentran todos en el mismo plano. Dejar\(r_e \) ser el radio de la tierra, dejar\(r_s \) ser la distancia desde el centro de la tierra hasta el satélite (llamado el radio orbital del satélite), y dejar\(d \) ser la distancia desde la estación terrestre hasta el satélite. Dejar\(E \) ser el ángulo de elevación desde la estación terrestre hasta el satélite, y dejar\(\gamma \) y\(\psi \) ser los ángulos que se muestran en la Figura 2.25.

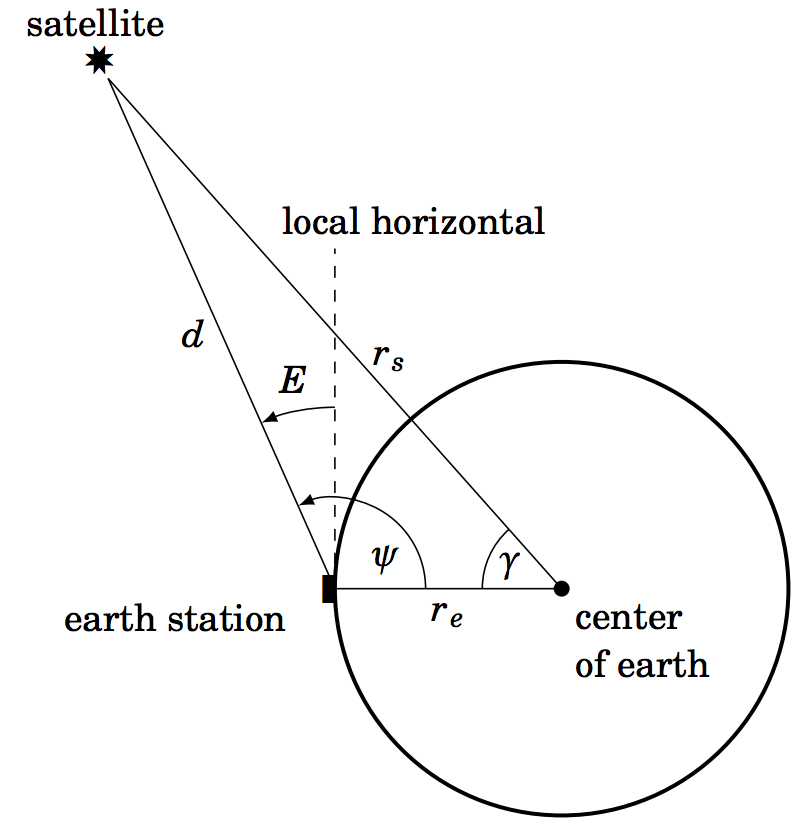
Figura 2.2.5

Usa la Ley de Cosinos para mostrar que
\ [
d ~=~ r_s\,\ sqrt {1\; +\;\ left (\ frac {r_e} {r_s}\ derecha) ^2\; -\; 2\,\ left (\ frac {r_e} {r_s}\ derecha)
\,\ cos\;\ gamma} ~~,
\]
y luego usar\(E=\psi-90^\circ \) y la Ley de los Pinos para demostrar que
\ [
\ cos\; E ~=~\ dfrac {\ sin\;\ gamma} {\ sqrt {1\; +\;\ left (\ dfrac {r_e} {r_s}\ derecha) ^2\; -\;
2\,\ left (\ dfrac {r_e} {r_s}\ derecha)\,\ cos\;\ gamma}} ~.
\]
Nota: Esta fórmula permite calcular el ángulo de elevación\(E \) a partir de las coordenadas de la estación terrestre y el punto del subsatélite (donde la línea desde el satélite hasta el centro de la tierra cruza la superficie de la tierra).

---

2.3 Ejercicios

Para los Ejercicios 1-3, usa la Ley de Tangentes para resolver el triángulo\(\triangle\,ABC \).

2.3.1\(a = 12 \),\(b = 8 \),\(C = 60^\circ\)

2.3.2\(A = 30^\circ \),\(b = 4 \),\(c = 6\)

2.3.3\(a = 7 \),\(B = 60^\circ \),\(c = 9\)

Para los Ejercicios 4-6, verifique si es posible que un triángulo tenga las partes dadas.

2.3.4\(a=5 \),\(b=7 \),\(c=10 \),\(A=27.7^\circ \),\(B=40.5^\circ \),,\(C=111.8^\circ\)

2.3.5\(a=3 \),\(b=7 \),\(c=9 \),\(A=19.2^\circ \),\(B=68.2^\circ \),\(C=92.6^\circ\)

2.3.6\(a=6 \),\(b=9 \),\(c=9 \),\(A=39^\circ \),\(B=70.5^\circ \),\(C=70.5^\circ\)

2.3.7 Let\(\triangle\,ABC \) Ser un triángulo rectángulo con\(C=90^\circ \). \(\;\tan\;\frac{1}{2}(A-B) =\frac{a-b}{a+b}\, \)Demuéstralo.

2.3.8 Para cualquier triángulo\(\triangle\,ABC \), muéstrale eso\(\;\tan\;\frac{1}{2}(A-B) = \frac{a-b}{a+b}\;\cot\;\frac{1}{2}C\, \).

2.3.9 Para cualquier triángulo\(\triangle\,ABC \), demuéstrale eso\(\;\tan\;A = \dfrac{a\;\sin\;B}{c - a\;\cos\;B}\, \). (Sugerencia: Dibuja la altitud desde el vértice\(C \) hasta\(\overline{AB} \).) Observe que esta fórmula proporciona otra forma de resolver un triángulo en el Caso 3 (dos lados y el ángulo incluido).

2.3.10 Para cualquier triángulo\(\triangle\,ABC \), demuéstralo\(\;c = b\;\cos\;A + a\;\cos\;B\, \). Esta es otra comprobación de un triángulo.

2.3.11 Si\(\,b\;\cos\;A = a\;\cos\;B\, \), mostrar que el triángulo\(\triangle\,ABC \) es isósceles.

2.3.12 Dejar\(ABCD \) ser un cuadrilátero que contenga completamente sus dos diagonales. El cuadrilátero tiene ocho partes: cuatro lados y cuatro ángulos. ¿Cuál es el menor número de piezas que necesitarías saber para resolver el cuadrilátero? Explica tu respuesta.

---

2.4 Ejercicios

Para los Ejercicios 1-6, encuentra el área del triángulo\(\triangle\,ABC \).

2.4.1\(A = 70^\circ \),\(b = 4 \),\(c = 12\)

2.4.2\(a = 10 \),\(B = 95^\circ \),\(c = 35\)

2.4.3\(A = 10^\circ \),\(B = 48^\circ \),\(C = 122^\circ \),\(c = 11\)

2.4.4\(A = 171^\circ \),\(B = 1^\circ \),\(C = 8^\circ \),\(b = 2\)

2.4.5\(a = 2 \),\(b = 3 \),\(c = 4\)

2.4.6\(a = 5 \),\(b=6 \),\(c = 5\)

2.4.7 Encuentre el área del cuadrilátero en la Figura 2.4.3 a continuación.

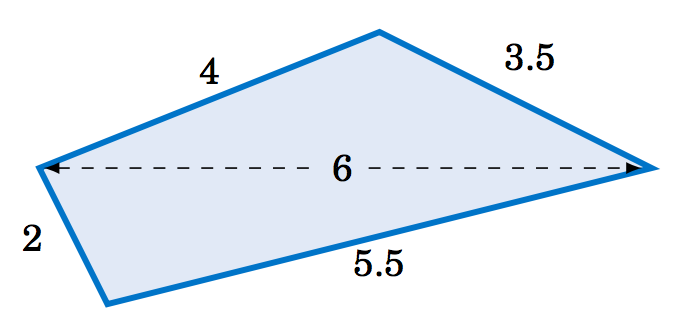
Figura 2.4.3 Ejercicio 7

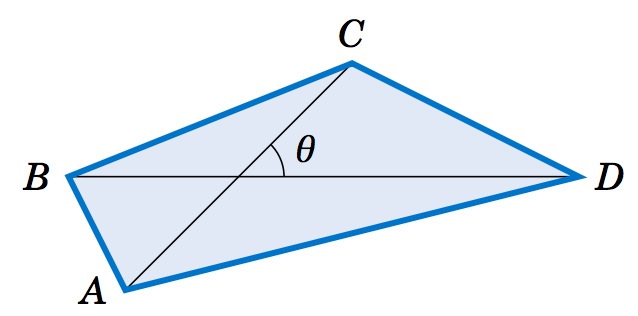
Figura 2.4.4 Ejercicio 8

2.4.8 Dejar\(ABCD \) ser un cuadrilátero que contenga completamente sus dos diagonales, como en la Figura 2.4.4 anterior. Demostrar que el área\(K \) de\(ABCD \) es igual a la mitad del producto de sus diagonales y el seno del ángulo que forman, i.e\(K = \frac{1}{2}\,AC\,\cdot\,BD\;\sin\;\theta\; \).

2.4.9 De la Ecuación 2.26 derivar la siguiente fórmula para el área de un triángulo\(\triangle\,ABC\):

\ [\ text {Área} ~=~ K ~=~\ frac {a^2\;\ sin\; B\;\ sin\; C} {2\;\ sin\ ;( B+C)}
\]
2.4.10 Mostrar que la fórmula del área del triángulo
\ [
\ text {Área} ~=~ K ~=~\ tfrac {1} {4}\,\ sqrt {(a + (b+c))\, (c - (a-b))\, (c + (a-b))\, (a + (b-c))}
\]
es equivalente a la fórmula de Heron. (Pista: En la fórmula de Heron reemplazar\(s \) por\(\frac{1}{2}(a+b+c) \).)
2.4.11 Mostrar que el área del triángulo Ecuación 2.34 es equivalente a la fórmula de Heron. (Pista: Factorar la expresión dentro de la raíz cuadrada. )

2.4.12 Encuentra el ángulo\(A \) en el Ejemplo 2.16, luego usa la Ecuación 2.23 para encontrar el área. ¿Funcionó?

---

2.5 Ejercicios

Para los Ejercicios 1-6, encuentra los radios\(R \) y\(r \) de los círculos circunscritos e inscritos, respectivamente, del triángulo\(\triangle\,ABC \).

2.5.1\(a = 2 \),\(b = 4 \),\(c = 5\)

2.5.2\(a = 6 \),\(b = 8 \),\(c = 8\)

2.5.3\(a = 5 \),\(b = 7 \),\(C = 40^\circ\)

2.5.4\(A = 170^\circ \),\(b = 100 \),\(c = 300\)

2.5.5\(a = 10 \),\(b = 11 \),\(c = 20.5\)

2.5.6\(a = 5 \),\(b = 12 \),\(c = 13\)

Para los Ejercicios 7 y 8 , dibuje el triángulo\(\triangle\,ABC \) y sus círculos circunscritos e inscritos con precisión, usando una regla y brújula (o software de computadora).

2.5.7\(a = 2 \) in,\(b = 4 \) in,\(c = 5 \) in

2.5.8\(a = 5 \) in,\(b = 6 \) in,\(c = 7 \) in

2.5.9 Para cualquier triángulo\(\triangle\,ABC \), let\(s = \frac{1}{2}(a+b+c) \). Mostrar que
\ [
\ tan\;\ tfrac {1} {2} A ~=~\ sqrt {\ frac {(s-b)\, (s-c)} {s\, (s-a)}} ~~, ~~~
\ tan\;\ tfrac {1} {2} B ~=~\ sqrt {\ frac {(s-a)\, (s-c)} {s\, (s-b)}} ~~, ~~~
\ tan\;\ tfrac {1} {2} C ~=~\ sqrt {\ frac {(s-a)\, (s-b)} {s\, (s-c)}} ~~.
\]
2.5.10 Mostrar que para cualquier triángulo\(\triangle\,ABC \), el radio\(R \) de su círculo circunscrito es
\ [
R ~=~\ frac {abc} {\ sqrt {(a+b+c)\, (b+c-a)\, (a-b+c)\, (a+b-c)}} ~~.
\]
2.5.11 Mostrar que para cualquier triángulo\(\triangle\,ABC \), el radio\(R \) de su círculo circunscrito y el radio\(r \) de su círculo inscrito satisfacen la relación
\ [
rR ~=~\ frac {abc} {2\, (a+b+c)} ~~.
\]
2.5.12 Dejar\(\triangle\,ABC \) ser un triángulo equilátero cuyos lados son de longitud\(a \).

(a) Encontrar el valor exacto del radio\(R \) del círculo circunscrito de\(\triangle\,ABC \).
(b) Encontrar el valor exacto\(r \) del radio del círculo inscrito de\(\triangle\,ABC \).
c) ¿Cuánto más grande es\(R \) que\(r\)?
d) Demostrar que los círculos circunscritos e inscritos de\(\triangle\,ABC \) tienen el mismo centro.

2.5.13 Dejar\(\triangle\,ABC \) ser un triángulo rectángulo con\(C=90^\circ \). \(\;\tan\;\tfrac{1}{2}A = \sqrt{\frac{c-b}{c+b}}~ \)Demuéstralo.