3.E: Identidades (Ejercicios)

3.1 Ejercicios

3.1.1 Eso lo demostramos\(\;\sin\;\theta ~=~ \pm\,\sqrt{1 ~-~ \cos^2 \;\theta}\; \) para todos\(\theta \). Dé un ejemplo de un ángulo\(\theta \) tal que\(\sin\;\theta ~=~ -\sqrt{1 ~-~ \cos^2 \;\theta}\; \).

3.1.2 Eso lo demostramos\(\;\cos\;\theta ~=~ \pm\,\sqrt{1 ~-~ \sin^2 \;\theta}\; \) para todos\(\theta \). Dé un ejemplo de un ángulo\(\theta \) tal que\(\cos\;\theta ~=~ -\sqrt{1 ~-~ \sin^2 \;\theta}\; \).

3.1.3 Supongamos que se le da un sistema de dos ecuaciones de la siguiente forma:

\ [\ nonumber\ begin {alinear*}
A\,\ cos\;\ phi ~ &= ~ B\,\ nu_1 ~-~ B\ nu_2\;\ cos\;\ theta\\\ nonumber
A\,\ sin\;\ phi ~ &= ~ B\,\ nu_2\;\ sin\;\ theta ~.
\ end {align*}\ nonumber\]

\(\;A ^2 ~=~ B^2 \left( \nu_1^2 ~+~ \nu_2^2 ~-~ 2\nu_1 \nu_2 \;\cos\theta\ \right) \)Demuéstralo.

Para los Ejercicios 4-16, acreditar la identidad dada.

3.1.4\(\cos\;\theta ~ \tan\;\theta ~=~ \sin\;\theta\)

3.1.5\(\sin\;\theta ~ \cot\;\theta ~=~ \cos\;\theta\)

3.1.6\(\dfrac{\tan\;\theta}{\cot\;\theta} ~=~ \tan^2 \;\theta\)

3.1.7\(\dfrac{\csc\;\theta}{\sin\;\theta} ~=~ \csc^2 \;\theta\)

3.1 .8\(\dfrac{\cos^2 \;\theta}{1 ~+~ \sin\;\theta} ~=~ 1 ~-~ \sin\;\theta\)

3.1.9\(\dfrac{1 ~-~ 2\;\cos^2 \;\theta}{\sin\;\theta ~ \cos\;\theta} ~=~ \tan\;\theta ~-~ \cot\;\theta\)

3.1.10\(\sin^4 \;\theta ~-~ \cos^4 \;\theta ~=~ \sin^2 \;\theta ~-~ \cos^2 \;\theta\)

3.1.11\(\cos^4 \;\theta ~-~ \sin^4 \;\theta ~=~ 1 ~-~ 2\;\sin^2 \;\theta\)

3.1.12\ (\ dfrac {1 ~-~\ tan\;\ theta} {1 ~+~\ tan\;\ theta} ~=~
\ dfrac {\ cuna\;\ theta ~-~ 1} {\ cuna\;\ theta ~+~ 1}\)

3.1.13\ (\ dfrac {\ tan\;\ theta ~+~\ tan\;\ phi} {\ cuna\;\ theta ~+~\ cuna\;\ phi} ~=~
\ tan\;\ theta ~\ tan\;\ phi\)

3.1.14 \(\dfrac{\sin^2 \;\theta}{1 ~-~ \sin^2 \;\theta} ~=~ \tan^2 \;\theta\)

3.1.15\(\dfrac{1 ~-~ \tan^2 \;\theta}{1 ~-~ \cot^2 \;\theta} ~=~ 1 ~-~ \sec^2 \;\theta\)

3.1.16\ (\ sin\;\ theta ~=~\ pm\,\ dfrac {\ tan\;\ theta} {\ sqrt {1 ~+~
\ tan^2\;\ theta}}\ qquad\) (Pista: Resolver para\(\;\sin^2 \theta\; \) en el Ejercicio 14. )

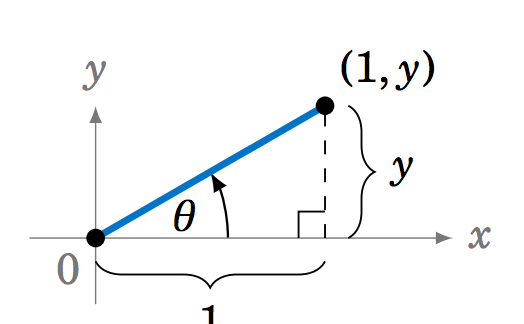
3.1.17 A veces las identidades pueden ser probadas por métodos geométricos. Por ejemplo, para probar la identidad en el Ejercicio 16, dibuje un ángulo agudo\(\theta \) en QI y elija el punto\((1,y) \) en su lado terminal, como en la Figura 3.1.2. ¿Qué debe ser\(y \) igual? Utilízalo para acreditar la identidad por aguda\(\theta \). Explica los ajustes que necesitarías hacer en la Figura 3.1.2 para acreditar la identidad\(\theta \) en los otros cuadrantes. ¿Se mantiene la identidad si\(\theta \) está en cualquiera de los ejes?

Figura 3.1.2

3.1.18 Similar al Ejercicio 16, encontrar una expresión para\(\cos\;\theta \) únicamente en términos de\(\tan\;\theta \).

3.1.19 Encontrar una expresión para\(\tan\;\theta \) únicamente en términos de\(\sin\;\theta \), y uno únicamente en términos de\(\cos\;\theta \).

3.1.20 Supongamos que un punto con coordenadas\((x,y)=(a\;(\cos\;\psi\;-\;\epsilon),a\sqrt{1 - \epsilon^2}~\sin\;\psi)\) es una\(r>0 \) distancia del origen, dónde\(a>0 \) y\(0 < \epsilon < 1 \). \(\;r^2 = x^2 + y^2\)Utilízalo para mostrar eso\(\;r = a\;(1 \;-\; \epsilon\;\cos\;\psi)\; \). \\ (Nota: Estas coordenadas surgen en el estudio de órbitas elípticas de planetas.)

3.1.21 Mostrar que cada función trigonométrica se puede poner en términos de la función sinusoidal.

---

3.2 Ejercicios

3.2.1 Verificar las fórmulas de adición 3.12 y 3.13 para\(A=B=0^\circ \).

Para los Ejercicios 2 y 3, encuentra los valores exactos de\(\sin\;(A+B) \),\(\cos\;(A+B) \), y\(\tan\;(A+B) \).

3.2.2\(\sin\;A = \frac{8}{17} \),\(\cos\;A = \frac{15}{17} \),\(\sin\;B = \frac{24}{25} \),
\(\cos\;B = \frac{7}{25}\)

3.2.3\(\sin\;A = \frac{40}{41} \),\(\cos\;A = \frac{9}{41} \),\(\sin\;B = \frac{20}{29} \),
\(\cos\;B = \frac{21}{29}\)

3.2.4 Uso \(75^\circ = 45^\circ + 30^\circ \)para encontrar el valor exacto de\(\;\sin\;75^\circ \).

3.2.5 Utilícelo\(15^\circ = 45^\circ - 30^\circ \) para encontrar el valor exacto de\(\;\tan\;15^\circ \).

3.2.6 Demostrar la identidad\(\;\sin\;\theta + \cos\;\theta = \sqrt{2}\;\sin\;(\theta + 45^\circ)\; \). Explique por qué esto demuestra que

\ [-\ sqrt {2} ~\ le~\;\ sin\;\ theta ~+~\ cos\;\ theta ~\ le~\ le~\ sqrt {2}
\ nonumber\]

para todos los ángulos\(\theta \). ¿Para cuál\(\theta \) entre\(0^\circ \) y\(360^\circ \)\(\;\sin\;\theta \;+\; \cos\;\theta\; \) sería el más grande?

Para los Ejercicios 7-14, acreditar la identidad dada.

3.2.7\ (\ cos\ ;( A+B+C)\; =\;\ cos\; A~\ cos\; B~\ cos\; C\; -
\;\ cos\; A~\ sin\; B~\ sin\; C\; -\ sin\; A~\ cos\; B~\ sin\; C\; -\ sin\; A~\ pecado\; B~\ cos\; C\)

3.2.8\ (\ tan\ ;( A+B+C) ~=~\ dfrac {\ tan\; A\; +\;\ tan\; B\; +\;\ tan\; C\; -\;
\ tan\; A~\ tan\; B~\ tan\; C} {1\; -\;\ tan\; B~\ tan\; C\; -\ tan\; A~\ tan\; A~\ tan\; C\; -
\ tan\; A~\ tan\; B}\)

3.2.9\(\cot\;(A+B) ~=~ \dfrac{\cot\;A~\cot\;B \;-\; 1}{\cot\;A \;+\; \cot\;B}\)

3.2.10\(\cot\;(A-B) ~=~ \dfrac{\cot\;A~\cot\;B \;+\; 1}{\cot\;B \;-\; \cot\;A}\)

3.2.11\(\tan\;(\theta + 45^\circ) ~=~ \dfrac{1 \;+\; \tan\;\theta}{1 \;-\; \tan\;\theta}\)

3.2.12\(\dfrac{\cos\;(A+B)}{\sin\;A~\cos\;B} ~=~ \cot\;A \;-\; \tan\;B\)

3.2.13\(\cot\;A ~+~ \cot\;B ~=~ \dfrac{\sin\;(A+B)}{\sin\;A~\sin\;B}\)

3.2.14\ (\ dfrac {\ sin\ ;( A-B)} {\ sin\ ;( A+B)} ~=~
\ dfrac {\ cot\; B\; -\;\ cuna\; A} {\ cuna\; B\; +\;\ cuna\; A}\)

3.2.15 Generalizar Ejercicio 6: Para cualquier\(a \) y\(b \),\(-\sqrt{a^2 + b^2} \;\le\; a\;\sin\;\theta \;+\; b\;\cos\;\theta \;\le\; \sqrt{a^2 + b^2}\; \) para todos\(\theta \).

3.2.16 Continuando Ejemplo 3.12, utilizar la ley de Snell para mostrar que el coeficiente de Fresnel de transmisión de polarización s

\ [\ tag {3.22}
t_ {1\; 2\; s} ~=~\ frac {2\; n_1 ~\ cos\;\ theta_1} {n_1 ~\ cos\;\ theta_1 ~+~ n_2 ~\ cos\;\ theta_2}
\ nonumber\]

se puede escribir como:

\ [t_ {1\; 2\; s} ~=~\ frac {2\;\ cos\;\ theta_1~\ sin\;\ theta_2} {\ sin\; (\ theta_2 +\ theta_1)}
\ nonumber\]

3.2.17 Supongamos que dos líneas con pendientes\(m_1 \) y\(m_2 \), respectivamente, se cruzan en ángulo\(\theta \) y no son perpendiculares (es decir\(\theta \ne 90^\circ\)), como en la figura de la derecha. Demostrar que

\ [\ tan\;\ theta ~=~\ izquierda|\ frac {m_1 ~-~ m_2} {1 ~+~ m_1\; m_2}\ derecha| ~.
\ nonumber\]

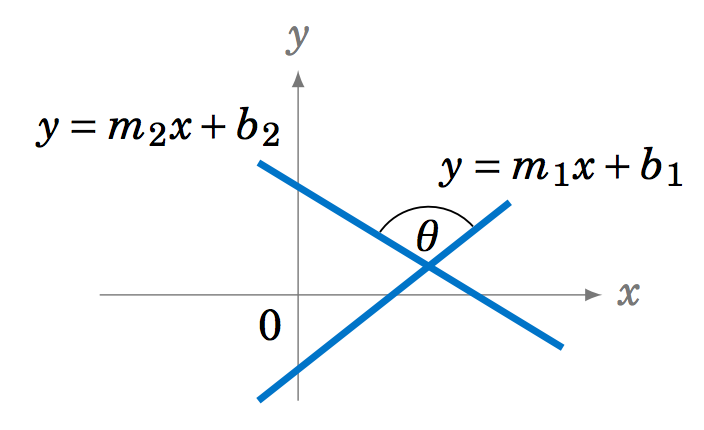
(Pista: Utilice el Ejemplo 1.26 de la Sección 1.5.)

3.2.18 Usa el Ejercicio 17 para encontrar el ángulo entre las líneas\(y=2x+3 \) y\(y=-5x-4 \).

3.2.19 Para cualquier triángulo\(\triangle\,ABC \), mostrar que\ (\;\ cuna\; A~\ cuna\; B ~+~\ cuna\; B~\ cuna\; C ~+~
\ cuna\; C~\ cuna\; A ~=~ 1\).
(Pista: Use el Ejercicio 9 y\(C=180^\circ - (A+B) \).)

3.2.20 Para cualquier ángulo positivo\(A \),\(B \), y\(C \) tal que\(A+B+C=90^\circ \), mostrar que

\ [\ tan\; A~\ tan\; B ~+~\ tan\; B~\ tan\; C ~+~\ tan\; C~\ tan\; A ~=~ 1 ~.
\ nonumber\]

3.2.21 Demostrar la identidad\(\;\sin\;(A+B)~\cos\;B ~-~ \cos\;(A+B)~\sin\;B ~=~ \sin\;A \). Tenga en cuenta que el lado derecho depende solo de\(A \), mientras que el lado izquierdo depende de ambos\(A \) y\(B \).

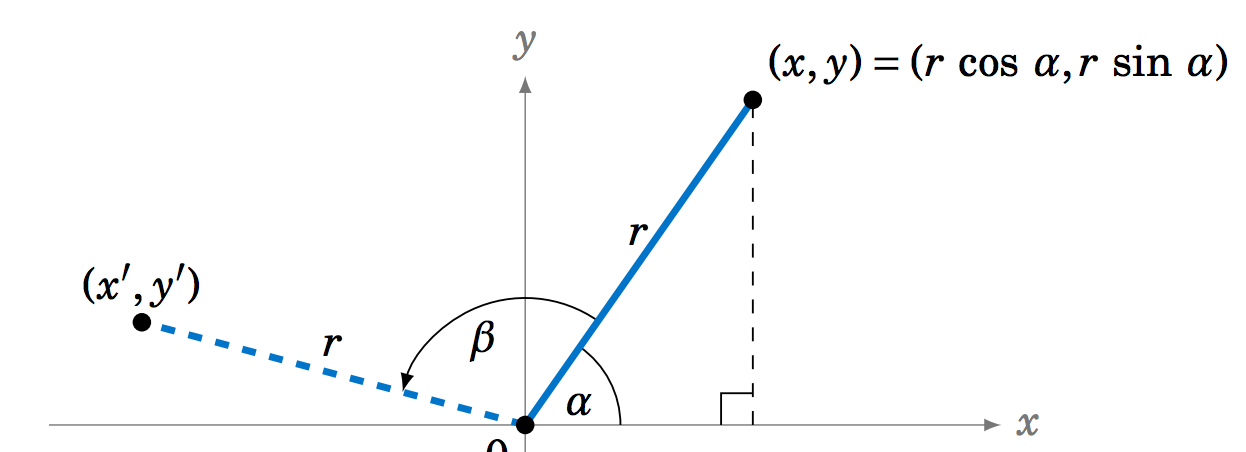
3.2.22 Un segmento de línea de longitud\(r > 0 \) desde el origen hasta el punto\((x,y) \) hace un ángulo\(\alpha \) con el\(x\) eje positivo, de manera que\((x,y) = (r\;\cos\;\alpha,r\;\sin\;\alpha) \), como en la figura de abajo. ¿Cuáles son las nuevas coordenadas del punto final\((x',y') \) después de una rotación en sentido antihorario por un ángulo\(\beta\;\)? Tu respuesta debe ser en términos de\(r \),\(\alpha \), y\(\beta \).

---

3.3 Ejercicios

Para los Ejercicios 1-8, acreditar la identidad dada.

3.3.1\(\cos\;3\theta ~=~ 4\;\cos^3 \;\theta ~-~ 3\;\cos\;\theta\)

3.3.2\(\tan\;\tfrac{1}{2}\theta ~=~ \csc\;\theta ~-~ \cot\;\theta\)

3.3.3\(\dfrac{\sin\;2\theta}{\sin\;\theta} ~-~ \dfrac{\cos\;2\theta}{\cos\;\theta} ~=~ \sec\;\theta\)

3.3.4\(\dfrac{\sin\;3\theta}{\sin\;\theta} ~-~ \dfrac{\cos\;3\theta}{\cos\;\theta} ~=~ 2\)

3.3.5 \(\tan\;2\theta ~=~ \dfrac{2}{\cot\;\theta \;-\; \tan\;\theta}\)

3.3.6\(\tan\;3\theta ~=~ \dfrac{3\;\tan\;\theta \;-\; \tan^3 \;\theta}{1 \;-\; 3\;\tan^2 \;\theta}\)

3.3.7\(\tan^2 \;\tfrac{1}{2}\theta ~=~ \dfrac{\tan\;\theta \;-\; \sin\;\theta}{\tan\;\theta \;+\; \sin\;\theta}\)

3.3.8\ (\ dfrac {\ cos^2\;\ psi} {\ cos^2\;\ theta} ~=~\ dfrac {1\; +\;\ cos\; 2\ psi} {1\; +\;
\ cos\; 2\ theta}\)

3.3.9 Algunos libros de texto de trigonometría utilizados para afirmar incorrectamente que\(\;\sin\;\theta ~+~ \cos\;\theta ~=~ \sqrt{1 \;+\; \sin\;2\theta} \) era una identidad. Dé un ejemplo de un ángulo específico\(\theta \) que haría falsa esa ecuación. ¿Es\(\;\sin\;\theta ~+~ \cos\;\theta ~=~ \pm\;\sqrt{1 \;+\; \sin\;2\theta} \) una identidad? Justifica tu respuesta.

3.3.10 Rellene el resto de la tabla a continuación para los ángulos\(0^\circ < \theta < 720^\circ \) en incrementos de\(90^\circ \), mostrando\(\theta \)\(\tfrac{1}{2}\theta \), y los signos (\(+\)o\(-\)) de\(\sin\;\theta \) y\(\tan\;\tfrac{1}{2}\theta \).

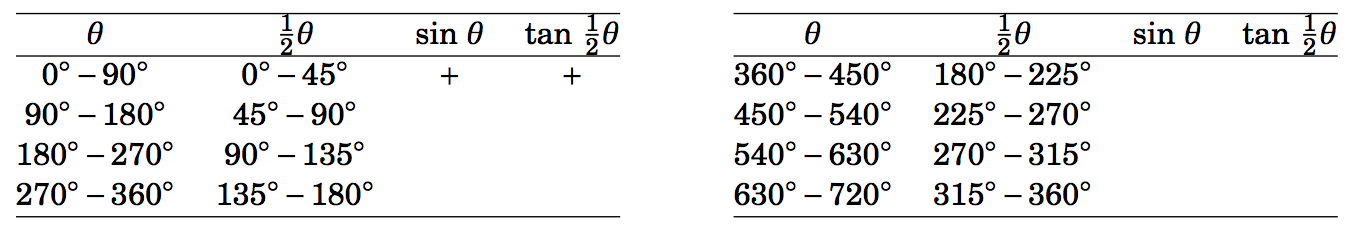
3.3.11 En general, ¿cuál es el mayor valor que\(\;\sin\;\theta~\cos\;\theta\; \) puede tomar? Justifica tu respuesta.

Para los Ejercicios 12-17, acreditar la identidad dada para cualquier triángulo rectángulo\(\triangle\,ABC \) con\(C=90^\circ \).

3.3.12\(\sin\;(A-B) ~=~ \cos\;2B\)

3.3.13\(\cos\;(A-B) ~=~ \sin\;2A\)

3.3.14\(\sin\;2A ~=~ \dfrac{2\;ab}{c^2}\)

3.3.15\(\cos\;2A ~=~ \dfrac{b^2 - a^2}{c^2}\)

3.3.16\(\tan\;2A ~=~ \dfrac{2\;ab}{b^2 - a^2}\)

3.3.17\(\tan\;\tfrac{1}{2}A ~=~ \dfrac{c - b}{a} ~=~ \dfrac{a}{c + b}\)

3.3.18 Ejercicio continuo 20 de la Sección 3.1, se puede demostrar que

\ [\ begin {alinear*}
r\ ;( 1\; -\;\ cos\;\ theta) ~&=~ a\ ;( 1\; +\;\ épsilon)\, (1\; -\;\ cos\;\ psi) ~, ~\ text {y}\\
r\ ;( 1\; +\;\ cos\;\ theta) ~&=~ a\ ;( 1\; -\;\ épsilon)\, (1\; +\;\ cos\;\ psi) ~,
\ end {align*}\ nonumber\]

donde\(\theta \) y siempre\(\psi \) están en el mismo cuadrante. \(\;\tan\;\tfrac{1}{2}\theta ~=~ \sqrt{\frac{1 \;+\; \epsilon}{1 \;-\; \epsilon}}~ \tan\;\tfrac{1}{2}\psi\; \)Demuéstralo.

---

3.4 Ejercicios

3.4.1 Probar la fórmula 3.38.

3.4.2 Probar fórmula 3.39.

3.4.3 Probar fórmula 3.40.

3.4.4 Probar la fórmula 3.41.

3.4.5 Probar fórmula 3.42.

3.4.6 Probar la fórmula 3.44.

3.4.7 Probar la segunda ecuación de Mollweide: Para cualquier triángulo\(\triangle\,ABC \),\(~\dfrac{a+b}{c} ~=~ \dfrac{\cos\;\tfrac{1}{2}(A-B)}{\sin\;\tfrac{1}{2}C}\).

3.4.8 Continuando Ejemplo 3.21, utilizar la ley de Snell para mostrar que el coeficiente de reflexión de la p-polarización de Fresnel

\ [\ tag {3.46}
r_ {1\; 2\; p} ~=~\ frac {n_2 ~\ cos\;\ theta_1 ~-~ n_1 ~\ cos\;\ theta_2} {n_2 ~\ cos\;\ theta_1 ~+~
n_1 ~\ cos\;\ theta_2}
\ nonumber\]

se puede escribir como:

\ [
r_ {1\; 2\; p} ~=~\ frac {\ tan\ ;(\ theta_1 -\ theta_2)} {\ tan\ ;(\ theta_1 +\ theta_2)}
\ nonumber\]

3.4.9 Hay una forma más general para la potencia instantánea\(p(t) = v(t)\;i(t) \) en un circuito eléctrico que la del Ejemplo 3.22. El voltaje\(v(t) \) y la corriente\(i(t) \) pueden ser dados por

\ [\ begin {alinear*}
v (t) ~&=~ v_m\;\ cos\ ;(\ omega t +\ theta) ~,\\
i (t) ~&=~ i_m\;\ cos\ ;(\ omega t +\ phi) ~,
\ end {align*}\ nonumber\]

donde\(\theta \) se llama el ángulo de fase. \(p(t) \)Demostrar que se puede escribir como

\ [
p (t) ~=~\ tfrac {1} {2}\, v_m\; i_m\;\ cos\ ;(\ theta -\ phi) ~+~
\ tfrac {1} {2}\, v_m\; i_m\;\ cos\ ;( 2\ omega t +\ theta +\ phi) ~.
\ nonumber\]

Para los Ejercicios 10-15, acreditar la identidad o desigualdad dada para cualquier triángulo\(\triangle\,ABC \).

3.4.10\ (\ sin\; A\; +\;\ sin\; B\; +\;\ sin\; C ~=~
4\;\ cos\;\ tfrac {1} {2} A~\ cos\;\ tfrac {1} {2} B~\ cos\;\ tfrac {1} {2} C\) (Pista: Ejemplo mímico 3.18 usando\((\sin\;A \;+\; \sin\;B) \;+\; (\sin\;C \;-\; \sin\;(A+B+C)) \).)

3.4.11\(\cos\;A \;+\; \cos\;(B-C) ~=~ 2\;\sin\;B~\sin\;C\)

3.4.12\(\sin\;2A \;+\; \sin\;2B \;+\; \sin\;2C ~=~ 4\;\sin\;A~\sin\;B~\sin\;C\) (Consejos: Agrupar\(\sin\;2B \) y\(\sin\;2C \) juntos, use la fórmula de doble ángulo para\(\sin\;2A \), use el Ejercicio 11. )

3.4.13\(\dfrac{a-b}{a+b} ~=~ \dfrac{\sin\;A \;-\; \sin\;B}{\sin\;A \;+\; \sin\;B}\)

3.4.14\(\cos\;\tfrac{1}{2}A ~=~ \sqrt{\dfrac{s\;(s-a)}{bc}}~~ \) y\(~~\sin\;\tfrac{1}{2}A ~=~ \sqrt{\dfrac{(s-b)\;(s-c)}{bc}}\; \),\; donde\(s=\tfrac{1}{2}(a+b+c)$\) (Pista: Usa la Ley de Cosinos para demostrarlo\(2bc\;(1 + \cos\;A) ~=~ 4s\;(s-a) \).)

3.4.15\ (\ tfrac {1} {2}\; (\ sin\; A\; +\;\ sin\; B) ~\ le~
\ sin\;\ tfrac {1} {2} (A+B)\) (Pista: Mostrar que\ (\ sin\;\ tfrac {1} {2} (A+B)\; -
\ tfrac {1}} {2}\ ;(\ sin\; A\; +\;\ sin\; B)\;\ ge\; 0\).)

3.4.16 En el Ejemplo 3.20, ¿qué ángulos\(A \)\(B \),,\(C \) dan el valor máximo de\(\cos\;A \;+\; \cos\;B \;+\; \cos\;C\;\)?